Can We Forecast Daily Oil Futures Prices? Experimental Evidence from Convolutional Neural Networks
Abstract
:1. Introduction
2. Neural Networks and Convolutional Neural Networks
3. Model Design
3.1. Method 1: Neural Networks
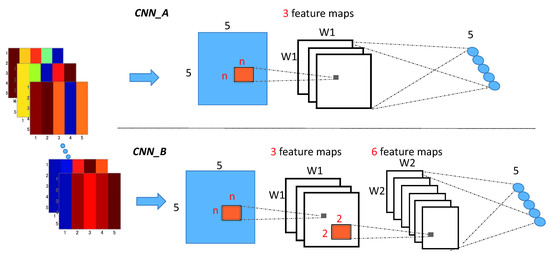
3.2. Method 2: Convolutional Neural Networks
4. Data
5. Empirical Results
5.1. Evaluation Criteria
5.2. Normalization Influence
5.3. Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alvarez-Ramirez, Jose, Eduardo Rodriguez, Esteban Martina, and Carlos Ibarra-Valdez. 2012. Cyclical behavior of crude oil markets and economic recessions in the period 1986–2010. Technological Forecasting and Social Change 79: 47–58. [Google Scholar] [CrossRef]
- Baumeister, Christiane, Pierre Guérin, and Lutz Kilian. 2015. Do high-frequency financial data help forecast oil prices? The MIDAS touch at work. International Journal of Forecasting 31: 238–52. [Google Scholar] [CrossRef]
- Bengio, Yoshua. 2009. Learning deep architectures for AI. Foundations and Trends® in Machine Learning 2: 1–127. [Google Scholar] [CrossRef]
- De Souza e Silva, Edmundo G., Luiz F.L. Legey, and Edmundo A. de Souza e Silva. 2010. Forecasting oil price trends using wavelets and hidden Markov models. Energy Economics 32: 1507–19. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Roberto S. Mariano. 1995. Comparing predictive accuracy. Journal of Business and Economic Statistics 13: 253–63. [Google Scholar]
- Drachal, Krzysztof. 2016. Forecasting spot oil price in a dynamic model averaging framework—Have the determinants changed over time? Energy Economics 60: 35–46. [Google Scholar] [CrossRef]
- Jammazi, Rania, and Chaker Aloui. 2012. Crude oil price forecasting: Experimental evidence from wavelet decomposition and neural network modeling. Energy Economics 34: 828–41. [Google Scholar] [CrossRef]
- Kingma, Diederik P., and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv, arXiv:1412.6980. [Google Scholar]
- Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E. Hinton. 2012. Imagenet classification with deep convolutional neural networks. Paper presented at the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, December 3–6; pp. 1097–105. [Google Scholar]
- LeCun, Yann, Bernhard E. Boser, John Denker, Don Henderson, Richard E. Howard, Wayne Hubbard, and Larry Jackel. 1989. Backpropagation applied to handwritten zip code recognition. Neural Computation 1: 541–51. [Google Scholar] [CrossRef]
- Ma, Xiaolei, Zhuang Dai, Zhengbing He, Jihui Na, Yong Wang, and Yunpeng Wang. 2017. Learning traffic as images: A deep convolutional neural network for large-scale transportation network speed prediction. Sensors 17: 818. [Google Scholar] [CrossRef] [PubMed]
- Merino, Antonio, and Álvaro Ortiz. 2005. Explaining the so-called “price premium” in oil markets. OPEC Energy Review 29: 133–52. [Google Scholar] [CrossRef]
- Moshiri, Source, and Faezeh Foroutan. 2006. Forecasting nonlinear crude oil futures prices. The Energy Journal 27: 81–95. [Google Scholar] [CrossRef]
- Naser, Hanan. 2016. Estimating and forecasting the real prices of crude oil: A data rich model using a dynamic model averaging (DMA) approach. Energy Economics 56: 75–87. [Google Scholar] [CrossRef]
- Ongkrutaraksa, Worapot. 1995. Fractal Theory and Neural Networks in Capital Markets. Working Paper at Kent State University. Kent: Kent State University. [Google Scholar]
- Refenes, Apostolos Paul. 1994. Neural Networks in the Capital Markets. New York: John Wiley & Sons, Inc. [Google Scholar]
- Simonyan, Karen, and Andrew Zisserman. 2014. Two-stream convolutional networks for action recognition in videos. In Advances in Neural Information Processing Systems. Cambridge: MIT Press, pp. 568–76. [Google Scholar]
- Sklibosios Nikitopoulos, Christina, Matthew Squires, Susan Thorp, and Danny Yeung. 2017. Determinants of the crude oil futures curve: Inventory, consumption and volatility. Journal of Banking and Finance 84: 53–67. [Google Scholar] [CrossRef]
- Tang, Mingming, and Jinliang Zhang. 2012. A multiple adaptive wavelet recurrent neural network model to analyze crude oil prices. Journal of Economics and Business 64: 275–86. [Google Scholar]
- Wang, Shouyang, Lean Yu, and Kin Keung Lai. 2005. Crude oil price forecasting with TEI@ I methodology. Journal of Systems Science and Complexity 18: 145–66. [Google Scholar]
- Wang, Yudong, Chongfeng Wu, and Li Yang. 2016. Forecasting crude oil market volatility: A Markov switching multifractal volatility approach. International Journal of Forecasting 32: 1–9. [Google Scholar] [CrossRef]
- Wen, Fenghua, Xu Gong, and Shenghua Cai. 2016. Forecasting the volatility of crude oil futures using HAR-type models with structural breaks. Energy Economics 59: 400–13. [Google Scholar] [CrossRef]
- Yu, Lean, Yang Zhao, and Ling Tang. 2017. Ensemble forecasting for complex time series using sparse representation and neural networks. Journal of Forecasting 36: 122–38. [Google Scholar] [CrossRef]
- Ye, Michael, John Zyren, and Joanne Shore. 2006. Forecasting short-run crude oil price using high-and low-inventory variables. Energy Policy 34: 2736–43. [Google Scholar] [CrossRef]
- Zeiler, Matthew D., and Rob Fergus. 2014. Visualizing and understanding convolutional networks. Paper presented at the European Conference on Computer Vision, Zurich, Switzerland, September 6–12; pp. 818–33. [Google Scholar]
- Zhao, Yang, Jianping Li, and Lean Yu. 2017. A deep learning ensemble approach for crude oil price forecasting. Energy Economics 66: 9–16. [Google Scholar] [CrossRef]
| 1. | In this paper, the short-term forecast means the next day forecast that is the forecast is 1-step-ahead. |
| 2. | In fact, we also used the 2 and 3 output layers and we find there are not obvious differences among 5 output nodes in forecast performance, which implies the robustness of our CNN models. |





| Models | Functions | Inputs | Layers | DA | RMAE | Theil’s U |
|---|---|---|---|---|---|---|
| NF | - | - | - | 0.495 | 0.909 | 1 |
| AR-GARCH | - | - | - | 0.450 | 0.910 | 1.000 |
| Sigmoid | Oil | 2 | 0.536 | 0.816 | 0.865 | |
| Sigmoid | Oil | 3 | 0.567 | 0.785 | 0.814 | |
| Sigmoid | Oil-delta | 2 | 0.541 | 0.801 | 0.832 | |
| Sigmoid | Oil-delta | 3 | 0.575 | 0.808 | 0.802 | |
| Tanh | Oil | 2 | 0.514 | 0.835 | 0.838 | |
| Tanh | Oil | 3 | 0.557 | 0.793 | 0.813 | |
| Tanh | Oil-delta | 2 | 0.545 | 0.811 | 0.821 | |
| Tanh | Oil-delta | 3 | 0.556 | 0.776 | 0.782 |
| Models | Functions | Inputs | Kernel Size | Layers | DA | RMAE | Theil’s U |
|---|---|---|---|---|---|---|---|
| NF | - | - | - | - | 0.495 | 0.909 | 1 |
| AR-GARCH | - | - | - | - | 0.450 | 0.910 | 1.000 |
| Sigmoid | Oil | 2 × 2 | 2 | 0.523 | 0.732 | 0.781 | |
| Sigmoid | Oil | 2 × 2 | 3 | 0.542 | 0.745 | 0.763 | |
| Sigmoid | Oil | 3 × 3 | 2 | 0.535 | 0.728 | 0.743 | |
| Sigmoid | Oil | 3 × 3 | 3 | 0.550 | 0.741 | 0.762 | |
| Tanh | Oil | 2 × 2 | 2 | 0.561 | 0.753 | 0.776 | |
| Tanh | Oil | 2 × 2 | 3 | 0.574 | 0.772 | 0.791 | |
| Tanh | Oil | 3 × 3 | 2 | 0.595 | 0.739 | 0.752 | |
| Tanh | Oil | 3 × 3 | 3 | 0.558 | 0.785 | 0.755 |
| Models | Functions | Inputs | Kernel Size | Layers | DA | RMAE | Theil’s U |
|---|---|---|---|---|---|---|---|
| NF | - | - | - | - | 0.415 | 1.363 | 1 |
| AR-GARCH | - | - | - | - | 0.400 | 1.374 | 1.001 |
| Sigmoid | Oil | 2 × 2 | 2 | 0.436 | 1.259 | 0.821 | |
| Sigmoid | Oil | 2 × 2 | 3 | 0.441 | 1.245 | 0.814 | |
| Sigmoid | Oil | 3 × 3 | 2 | 0.455 | 1.129 | 0.796 | |
| Sigmoid | Oil | 3 × 3 | 3 | 0.475 | 1.191 | 0.842 | |
| Tanh | Oil | 2 × 2 | 2 | 0.483 | 1.162 | 0.806 | |
| Tanh | Oil | 2 × 2 | 3 | 0.478 | 1.213 | 0.829 | |
| Tanh | Oil | 3 × 3 | 2 | 0.492 | 1.125 | 0.811 | |
| Tanh | Oil | 3 × 3 | 3 | 0.459 | 1.257 | 0.801 |
| Models | Function | Inputs | Kernel Size | Layers | DA | RMAE | Theil’s U |
|---|---|---|---|---|---|---|---|
| NF | - | - | - | - | 0.495 | 0.909 | 1 |
| AR-GARCH | - | - | - | - | 0.490 | 0.910 | 1.000 |
| Sigmoid | Oil | 2 × 2 | 2 | 0.505 | 0.891 | 0.983 | |
| Sigmoid | Oil | 2 × 2 | 3 | 0.517 | 0.863 | 0.956 | |
| Sigmoid | Oil | 3 × 3 | 2 | 0.495 | 0.851 | 0.942 | |
| Sigmoid | Oil | 3 × 3 | 3 | 0.523 | 0.865 | 0.923 | |
| Tanh | Oil | 2 × 2 | 2 | 0.491 | 0.874 | 0.996 | |
| Tanh | Oil | 2 × 2 | 3 | 0.501 | 0.881 | 0.962 | |
| Tanh | Oil | 3 × 3 | 2 | 0.525 | 0.884 | 0.950 | |
| Tanh | Oil | 3 × 3 | 3 | 0.519 | 0.785 | 0.956 |
| NF vs. AR-GARCH | NF vs. NN | NF vs. CNN | |
| Statistics | −0.313 | 4.039 | 3.640 |
| P-values | 0.755 | 0.000 | 0.000 |
| AR-GARCH vs. NN | AR-GARCH vs. CNN | NN vs. CNN | |
| Statistics | 4.035 | 3.635 | 2.308 |
| P-values | 0.000 | 0.000 | 0.023 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Cai, X.; Tanaka, K.; Takiguchi, T.; Kinkyo, T.; Hamori, S. Can We Forecast Daily Oil Futures Prices? Experimental Evidence from Convolutional Neural Networks. J. Risk Financial Manag. 2019, 12, 9. https://doi.org/10.3390/jrfm12010009
Luo Z, Cai X, Tanaka K, Takiguchi T, Kinkyo T, Hamori S. Can We Forecast Daily Oil Futures Prices? Experimental Evidence from Convolutional Neural Networks. Journal of Risk and Financial Management. 2019; 12(1):9. https://doi.org/10.3390/jrfm12010009
Chicago/Turabian StyleLuo, Zhaojie, Xiaojing Cai, Katsuyuki Tanaka, Tetsuya Takiguchi, Takuji Kinkyo, and Shigeyuki Hamori. 2019. "Can We Forecast Daily Oil Futures Prices? Experimental Evidence from Convolutional Neural Networks" Journal of Risk and Financial Management 12, no. 1: 9. https://doi.org/10.3390/jrfm12010009
APA StyleLuo, Z., Cai, X., Tanaka, K., Takiguchi, T., Kinkyo, T., & Hamori, S. (2019). Can We Forecast Daily Oil Futures Prices? Experimental Evidence from Convolutional Neural Networks. Journal of Risk and Financial Management, 12(1), 9. https://doi.org/10.3390/jrfm12010009