A Novel Multi-Phase Stochastic Model for Lithium-Ion Batteries’ Degradation with Regeneration Phenomena

Abstract

A lithium-Ion battery is a typical degradation product, and its performance will deteriorate over time. In its degradation process, regeneration phenomena have been frequently encountered, which affect both the degradation state and rate. In this paper, we focus on how to build the degradation model and estimate the lifetime. Toward this end, we first propose a multi-phase stochastic degradation model with random jumps based on the Wiener process, where the multi-phase model and random jumps at the changing point are used to describe the variation of degradation rate and state caused by regeneration phenomena accordingly. Owing to the complex structure and random variables, the traditional Maximum Likelihood Estimation (MLE) is not suitable for the proposed model. In this case, we treat these random variables as latent parameters, and then develop an approach for model identification based on expectation conditional maximum (ECM) algorithm. Moreover, depending on the proposed model, how to estimate the lifetime with fixed changing point is presented via the time-space transformation technique, and the approximate analytical solution is derived. Finally, a numerical simulation and a practical case are provided for illustration.

1. Introduction

Lithium-Ion battery as an important power source, has been widely used in our life and other industrial systems [1,2]. However, the performance of the battery will deteriorate with aging, which is embodied in the fading of its state of health (SOH) [3,4]. As a result, the remaining useful life (RUL) will be reduced, and further its deterioration may lead to an accident and even cause a huge loss. As such, it is meaningful to investigate how to estimate the lifetime and remaining useful life of Lithium-Ion battery. As an essential part of prognostic and health management (PHM), lifetime or remaining useful life (RUL) estimation can provide an effective information for maintenance decision to avoid the accident caused by its failure and reduce the safety risk [5,6,7]. So far, the methods of the lifetime estimation have been widely researched and gained momentum [8,9]. Especially, as analyzed by jardine [10], stochastic data-driven method has been widely investigated and applied to many degradation systems since it only relies on the available observed data and statistical models. Moreover, compared with other data-driven method, the stochastic data-driven method can capture the random dynamics and uncertainty of degradation processes. Therefore, we mainly concentrate on how to build a new stochastic data-driven model to describe the degradation trajectory of the Lithium-Ion battery and further estimate the lifetime and RUL based on the proposed model.

As to lifetime estimation for battery, the common way is to model the process of SOH, and then estimate and predict the RUL based on the proposed degradation model. It is well-known that the capacity fading of the battery can reflect its degradation of the SOH [3,11]. As a result, many researchers pay more attention to modeling the capacity degradation, and doing lifetime and RUL estimation based on the proposed model. For example, Tang et al. utilized Wiener process to describe the degradation process of battery and then predicted the RUL [12]. Hu et al. [13] and Dalal et al. [14] introduced how to model the degradation process of lithium-ion battery based on Kalman filter and particle filtering accordingly. Saha et al. proposed a relevance-vector-machines-based approach to evaluate the health state of battery [15]. To improve the long term prediction performance of the traditional AR model, Song et al., proposed an iterative nonlinear degradation-autoregressive model (IND-AR) model for RUL estimation of the spacecraft lithium-ion battery [16]. Panchal et al. had completed some degradation tests of batteries by using real world drive cycles collected from an electric vehicle, and further analyzed the impact of various discharge rates on electrical performance of the battery [17,18]. Especially, Pecht and his team performed many degradation tests for lithium-ion battery and obtained large amounts of degradation data, and then achieve a lot of valuable results depending on it [3,19,20]. However, there are still numerous problems needing to be further investigated in the future.

Capacity regeneration phenomena, also called the self-recovery phenomena in some other paper, means that the degradation capacity of the battery shows a sudden recovery after testing rest [21]. Such the regeneration phenomena will not only influence the degradation modeling but also the prediction of the lifetime (or RUL). Thus, it is meaningful to take consideration of regeneration phenomena into SOH prognostics and lifetime estimation of lithium-ion battery. So far, this issue has not been solved well and only a few of the researchers have focused on it. Liu et al. analyzed the mechanism of regeneration phenomena, and proposed a combination Gaussian process functional model to capture both degradation trend and regeneration [11]. Similarly, He et al. firstly used Wavelet analysis method to decouple global degradation trend, regeneration and fluctuations, and then modeled these three processes based on Gaussian process regression [22]. Orchard et al. formulated the state space model to describe the degradation process and then predicted the SOH via the particle filtering [21,23]. Although these works had considered the influence of regeneration phenomena on the degradation state, they did not pay attention to the variation of degradation rate caused by the regeneration phenomena. In fact, when the regeneration phenomenon appears, the degradation rate will be changed as will, which affects the results of lifetime and RUL estimation. Qin et al. built the relationship between the rest time and the regeneration phenomenon, and adopted Gaussian process to predict the global trend [24], where the state recovery caused by regeneration phenomenon was defined as a function of the rest time. Recently, Zhang et al. proposed a general degradation model for stochastic degrading systems with state recovery, and applied it into batteries’ degradation [25]. In [25], the two-state semi-Markov process was used to model the state switch i.e., the appearance of regeneration phenomena, and then the issue was transformed into the lifetime prediction under the random operating process. However, in these two works [24,25], the state recovery was regarded as the fixed value or fixed function so that its randomness and uncertainty was not taken into consideration. Therefore, regeneration phenomena provide a challenge for degradation modeling and lifetime prognostics.

In this paper, we attempt to deal with such the problem from the perspective of stochastic process and statistic analysis. First, we first proposed a multi-phase degradation with random jumps based on the Wiener process to describe the degradation process with regeneration phenomena. Second, we develop an approach for model identification based on expectation conditional maximum (ECM) algorithm to overcome the limitations of the traditional Maximum Likelihood Estimation (MLE) and Expectation Maximum (EM) algorithm owing to the complex structure and random variables. Third, we derive the approximate solution of lifetime estimation under the concept of the first passage time (FPT) via the time-scale transformation and the law of total probability. Finally, to illustrate the applicability and effectiveness of our method, a numerical example and a practical case of the battery are provided.

The remainder of the paper is organized as follows. In Section 2, the motivating example and problem formulation are introduced, and the general multi-phase degradation model with random jumps is formulated. Section 3 includes the main results of lifetime estimation. In Section 4, how to realize model identification is given. Two illustrative examples are presented to illustrate and demonstrate the proposed model in Section 5. This paper is concluded in Section 6.

2. Motivation and Problem Formulation

2.1. Motivation Example

As discussed in the literature [3,11,26], the capacity of the battery will be likely to recover after the battery rests during the charge/discharge procedure. For example, the following Figure 1a shows a set of testing data of lithium-ion battery (i.e., CS2-34) collected by the Center for Advanced Life Cycle Engineering (CALCE) of Maryland University, where the battery is prismatic and its capacity is 1100 mAh. What should be noted is that its charging profile is a standard constant current/constant voltage protocol with a constant current rate of 0.5 C until the voltage reaches 4.2 V, and then 4.2 V is sustained until the charging current drops to below 0.05 A. From the degradation data, several aspects should be noticed,

(1)

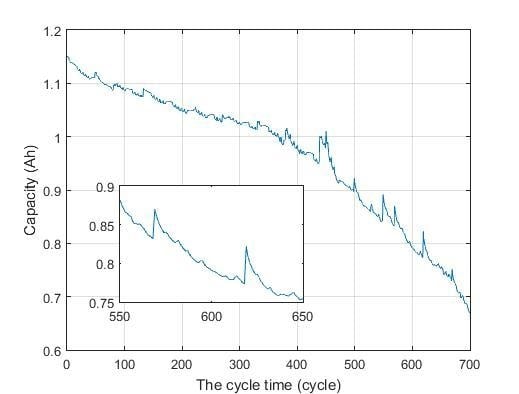
In the testing data from CALCE, the rest time lasts several and even more hours, which is caused by the pause between two continuous charge/discharge tests. Therefore, we classify the degradation process of the battery into several phases according to the rest time.

(2)

The rest time does not only lead to regeneration phenomenon i.e., degradation state recovery but also unchanging and further deterioration. In Figure 1c, the blue lines denote the differences of the degradation data at the point of rest time, and the red lines represent the differences at other points, which are collected from the other four batteries CS2-35, CS2-36, CS2-37, CS2-38. It is interesting to note that the statistical histograms of these two differences data are distinguished obviously, including their means and variances. In another word, all regeneration phenomena occur at the rest time, but it does not mean that each testing rest leads to regeneration phenomenon.

(3)

When a regeneration phenomenon occurs, not only the degradation state will increase suddenly, but also the degradation rate changes as shown in Figure 1b, which is the enlarged figure of Figure 1a for better illustration. It is noteworthy that the degradation rate will first increase heavily after a regeneration phenomenon appears, and then decrease gradually and finally return to that at the end of the previous phase.

However, most researchers only focus on parts of these three aspects, and few of them take a full consideration of the above three aspects for degradation modeling and lifetime estimation. So, it is essential to build an appropriate degradation model to satisfy such three features, and then estimate the lifetime and RUL based on the proposed model. As such, we attempt to propose a multi-phase degradation model with random jumps to handle all characters of such the state-recovery degradation trajectory, which is formulated as follows.

2.2. Formulation and Degradation Modeling

In this paper, we focus on the degradation model based on the stochastic process and statistical analysis. Let $X\left(t\right)$ denote the degradation process and then the lifetime, and then RUL under the concept of the FPT can be expressed as [9,27],

$$\begin{array}{c}\hfill T=\inf \{t:X\left(t\right)\ge \xi \left|X\left(0\right)\le \xi \right.\}\end{array}$$

(1)

where $\xi$ denotes the failure threshold which is usually defined as a constant value and determined by engineering practical condition. Then we make $f_T\left(t\right)$ represent the probability density function (PDF) of the lifetime and $F_T\left(t\right)$ denote the cumulative distribution function (CDF). In addition, the RUL usually draws more attention for an operating system. As usual, the RUL under the concept of the FPT is often defined as,

$$\begin{array}{c}\hfill L_k=\inf \{l_k:X(t_k+l_k)\ge \xi \left|X\left(t_k\right)\le \xi \right.\}\end{array}$$

(2)

where $l_k$ is the remaining useful life with PDF $f_{l_k}\left(t\right)$ and CDF $F_{l_k}\left(t\right)$ at time $t_k$.

In order to attain the lifetime and RUL estimation under the concept of the FPT, it is essential to establish an appropriate degradation model to fit the degradation trajectory. It is noted that if the regeneration phenomena occur, both the degradation state and rate will be affected and changed. As discussed before, the regeneration phenomenon is mainly related to the testing rest. In this paper, we treat the influence of testing rest as the non-fatal random shock, which will change the degradation state and rate randomly. Hence, inspired by multi-phase degradation model as many literatures [25,28], we propose a novel multi-phase degradation model with random jumps as follows,

$$\begin{array}{c}\hfill X\left(t\right)=X_0\left(t\right)+{\displaystyle \sum _{i=1}^{N\left(t\right)}}{X}_i\left(t\right)\end{array}$$

(3)

where $X\left(t\right)$ denotes the degradation process, $X_0\left(t\right)$ represents the traditional continuous degradation process without the effect of the testing rest, $X_i\left(t\right)$ reflects the change of degradation state and rate caused by i-th testing rest. In this way, the degradation process can be classified into $N\left(t\right)+1$ phases and each rest time can be regarded as the changing point, when there are $N\left(t\right)$ times of testing rest. It is defined that the all changing point time is prearranged and ${\tau }_i$ denotes the current time of the i-th changing point. Then, Equation (3) can be written as follows,

$$\begin{array}{c}\hfill X\left(t\right)=\left\{\begin{array}{cc}{X}_0\left(t\right)\hfill & 0t{\tau }_1\hfill \\ X_0\left(t\right)+{\sum }_{i=1}^1{X}_i\left(t\right)\hfill & {\tau }_1\le t{\tau }_2\hfill \\ X_0\left(t\right)+{\sum }_{i=1}^2{X}_i\left(t\right)\hfill & {\tau }_2\le t{\tau }_3\hfill \\ ⋮\hfill \\ X_0\left(t\right)+{\sum }_{i=1}^{n_{\tau }}{X}_i\left(t\right)\hfill & {\tau }_{n_{\tau }}-1\le t{\tau }_{n_{\tau }}\hfill \end{array}\right.\end{array}$$

(4)

where ${\tau }_{n_{\tau }}$ denotes total times of the changing points, i.e., ${\tau }_{n_{\tau }}=N\left(t_{\max }\right)$.

It is noteworthy that the continuous degradation trajectory of battery is not monotone, which makes the degradation models based on the monotone stochastic process (such as Gamma process [29], Inverse Gaussian process [30] and so on) not suitable. In this case, due to the non-monotonicity of the degradation process, we adopt Wiener process to describe the continuous degradation process $X_0\left(t\right)$, and it holds the following form,

$$\begin{array}{c}\hfill X_0\left(t\right)=x_0+\mu t+{\sigma }_{B}B\left(t\right)\end{array}$$

(5)

where $x_0$ is the initial value, t is the time, $B\left(t\right)$ is the standard Brownian motion, $\mu$ and ${\sigma }_B$ are purely time-dependent drift and diffusion coefficients.

Furthermore, based on the characters of the practical degradation data and inspired by the definition in [25,31], the negative exponential model is adopted to reflect the influence of the regeneration,

$$X_i\left(t\right)=\left\{\begin{array}{cc}-{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}+{\lambda }_3\hfill & \hspace{1em}t-{\tau }_i\ge 0\hfill \\ 0\hfill & t-{\tau }_{i}0\hfill \end{array}\right.$$

(6)

where ${\tau }_i$ denotes the time when the i-th testing rest occurs, $\mathbf{\lambda }=[{\lambda }_1,{\lambda }_2,{\lambda }_3]$ represents the parameters. It is worth mentioning that ${\lambda }_1+{\lambda }_3$ reflects the sudden change of the degradation state caused by the testing rest, and ${\lambda }_2$ describes its effect on the degradation rate. In order to better describe the randomness of the regeneration phenomena, it is assumed that ${\lambda }_1$ and ${\lambda }_3$ follow Gaussian distribution i.e., $N({\mu }_1,{\sigma }_1^2)$ and $N({\mu }_3,{\sigma }_3^2)$.

Next, we will discuss how to derive the RUL estimation under the of the FPT for such the proposed multi-phase degradation model.

3. Remaining Useful Life Estimation under the Concept of the FPT

In this section, we concentrate on how to attain the RUL estimation under the concept of the FPT. It is noted that the derivation of the FPT is affected by the form of $N\left(t\right)$. In this case, for simplicity we assume that the occurrence time of the rest time is prearranged and it is defined as a fixed value. We define that there are $n_{\tau }$ times of rest time, i.e., $N\left(t_{\max }\right)=n_{\tau }$. From Figure 2b, it could be found that the degradation rate will be increased suddenly and then recover gradually. As such, the following assumption is given,

Assumption A1.

It is assumed that each changed rate will recover to the initial value at the end of each degradation phase. That is to say, in Equation (6) $-{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}$ will approach to 0 and have no impact on the $(i+1)$-th phase, and only the effect of ${\lambda }_3$ is accumulated.

It is noted that due to the random jump caused by the regeneration phenomena, so the estimated PDF of the lifetime or RUL are not continuous at the changing point. Under this consideration, we will calculate the form of the lifetime under the concept of the FPT separately in different intervals subject to the degradation phase, i.e., $(0,{\tau }_1)$, $[{\tau }_{i-1},{\tau }_i)$ and $[{\tau }_{n_{\tau }},+\infty )$, where $i=2,3,\dots n_{\tau }$. Under the concept of the FPT, $T\in (0,{\tau }_1)$ means that the FPT of the degradation process only belongs to $(0,{\tau }_1)$, as well as $[{\tau }_{i-1},{\tau }_i)$ and $[{\tau }_{n_{\tau }},+\infty )$. For example, if $T\in [{\tau }_{i-1},{\tau }_i)$, for $\forall t{\tau }_{i-1}$ the degradation $X\left(t\right)\xi$. Therefore, we will attempt to derive the PDF of lifetime T in different intervals, i.e., $(0,{\tau }_1)$, $[{\tau }_{i-1},{\tau }_i)$ and $[{\tau }_{n_{\tau }},+\infty )$, where $i=2,3,\dots n_{\tau }$.

First of all, we focus on the simplest case, i.e., $T\in (0,{\tau }_1)$. It is noteworthy that $f_T\left(t\right)$ is only determined by the first degradation phase. Thus, we can easily obtain the expression of $f_T\left(t\right)$ through the property of the Wiener process.

$$\begin{array}{c}\hfill f_T\left(t\right)=\frac{1}{\sqrt{2\pi {\sigma }_B^2{t}^3}}\exp \left[-\frac{{(\xi -x_0-\mu t)}^2}{2{\sigma }_B^{2}t}\right],0t{\tau }_1\end{array}$$

(7)

where $x_0$ denotes the initial value and it is often set as 0 for simplicity.

However, it is not easy to derive the $f_T\left(t\right)$ at other intervals i.e., $[{\tau }_{i-1},{\tau }_i)$ and $[{\tau }_{n_{\tau }},+\infty )$ directly. In order to derive $f_T\left(t\right)$ at other intervals i.e., $[{\tau }_{i-1},{\tau }_i)$ and $[{\tau }_{n_{\tau }},+\infty )$, we first assume that $x_{{\tau }_i}$ denotes the degradation state at the changing point (or the rest time) ${\tau }_i$. Furthermore, let ${\tau }_i^{-}$ be the left limit of ${\tau }_i$, as well as $x_{{\tau }_i^{-}}$.

Remark 1.

It is worth mentioning that $x_{{\tau }_i^{-}}$ represents the degradation state at time $t={\tau }_i^{-}$. In fact, the real $x_{{\tau }_i^{-}}$ cannot be known and $x_{{\tau }_i^{-}}$ should be a random variable which is determined by the degradation models of the first i phases. Due to the influence of the rest time, it is noted that the left limit $x_{{\tau }_i^{-}}$ is not equal to $x_{{\tau }_i}$.

Then, under this assumption, degradation model at interval $[{\tau }_{i-1},{\tau }_i)$ and $[{\tau }_{n_{\tau }},+\infty )$ can be written as follows,

$$\begin{array}{cc}\hfill X\left(t\right)& =x_{{\tau }_i^{-}}+X_0(t-{\tau }_i)+X_i\left(t\right)\hfill \\ & =x_{{\tau }_i^{-}}+\mu (t-{\tau }_i)+{\sigma }_{B}B(t-{\tau }_i)-{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}+{\lambda }_3\hfill \end{array}$$

(8)

where if the degradation belongs to $[{\tau }_{n_{\tau }},+\infty )$, $x_{{\tau }_i^{-}}=x_{{\tau }_{n_{\tau }}}$.

In this way, we can find that the degradation model at each phase except the first phase is nonlinear. To obtain the FPT of the nonlinear degradation model, following Lemma 1 based on the time-scale transformation is introduced,

Lemma 1.

[27]: If the degradation model is defined as $x_0+s\left(t\right)+{\sigma }_B\left(t\right)$, its approximate PDF of lifetime can be obtain as follows,

$$\begin{array}{c}\hfill f_T\left(t\right)\cong \frac{1}{\sqrt{2\pi t}}\left[\frac{S\left(t\right)}{t}-\frac{dS\left(t\right)}{dt}\right]\exp \left[-\frac{S^2\left(t\right)}{2t}\right]\end{array}$$

(9)

where $S\left(t\right)=\frac{\xi -x_0-s\left(t\right)}{{\sigma }_B}$. In this way, we can easily obtain the approximate PDF of lifetime with fixed ${\lambda }_1$ and ${\lambda }_3$ according to the conclusion of Lemma 1.

$$\begin{array}{cc}\hfill f_T\left(t\right)\cong & \frac{1}{\sqrt{2\pi t}}\left[\frac{\xi -x_{{\tau }_i^{-}}+{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}+(t-{\tau }_i){\lambda }_2{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}-{\lambda }_1-{\lambda }_3}{{\sigma }_B(t-{\tau }_i)}\right]\hfill \\ & \times \exp \left[-\frac{{(\xi -x_{{\tau }_i^{-}}-\mu (t-{\tau }_i)+{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}-{\lambda }_1-{\lambda }_3)}^2}{2{\sigma }_B^2(t-{\tau }_i)}\right]\hfill \end{array}$$

(10)

where $t\in [{\tau }_{i-1},{\tau }_i)$ or $[{\tau }_{n_{\tau }},+\infty )$. As discussed before, ${\lambda }_1$, ${\lambda }_3$, and $x_{{\tau }_i^{-}}$ are random variables. To better illustrate, it is assumed that the PDFs of ${\lambda }_1$, ${\lambda }_3$, and $x_{{\tau }_i^{-}}$ are $p\left({\lambda }_1\right)$, $p\left({\lambda }_3\right)$, and $g(x_{{\tau }_i^{-}})$. It is noted that $g(x_{{\tau }_i^{-}})$ represents the transition probability from $x_0$ to $x_{{\tau }_i^{-}}$ under the concept of the FPT. In this way, the approximate PDF of the lifetime can be obtained according to the law of total probability as shown in following equation.

$$\begin{array}{cc}\hfill f_T\left(t\right)\cong & {\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{\xi }\frac{1}{\sqrt{2\pi (t-{\tau }_i)}}\left[\frac{\xi -x_{{\tau }_i^{-}}+{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}+(t-{\tau }_i){\lambda }_2{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}-{\lambda }_1-{\lambda }_3}{{\sigma }_B(t-{\tau }_i)}\right]\hfill \\ & \times \exp \left[-\frac{{(\xi -x_{{\tau }_i^{-}}-\mu (t-{\tau }_i)+{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}-{\lambda }_1-{\lambda }_3)}^2}{2{\sigma }_B^2(t-{\tau }_i)}\right]p\left({\lambda }_1\right)p\left({\lambda }_3\right)g(x_{{\tau }_i^{-}})d{x}_{{\tau }_i^{-}}d{\lambda }_{1}d{\lambda }_3\hfill \end{array}$$

(11)

where $t\in [{\tau }_{i-1},{\tau }_i)$ or $[{\tau }_{n_{\tau }},+\infty )$, ${\lambda }_1$ and ${\lambda }_3$ follow Gaussian distribution, but $x_{{\tau }_i^{-}}$ is unknown. It is worth mentioning that the PDFs of the lifetime exhibits in a form of the triple integration corresponding to three random variables, i.e., $x_{{\tau }_i^{-}}$, ${\lambda }_1$, and ${\lambda }_3$.

In order to obtain the PDF of lifetime, we must attain the PDF of $x_{{\tau }_i^{-}}$. What should be noticed that $g(x_{{\tau }_i^{-}})$ can be also regarded as the transition probability under an absorbing boundary ξ. Unfortunately, the analytical form of $g(x_{{\tau }_i^{-}})$ is hard to calculate owing to the nonlinear degradation model and the random jumps. Here we introduce an approximate way to deal with it.

Define $p(x_{{\tau }_i^{-}})$ as the transition probability from $x_0$ to $x_{{\tau }_i^{-}}$ without the absorbing boundary. Then depending on the proposed degradation model and the property of the Wiener process, we can obtain the form of $p(x_{{\tau }_i^{-}})$ as shown in following equation,

$$\begin{array}{c}\hfill p(x_{{\tau }_i^{-}})=\frac{1}{\sqrt{2\pi [{\sigma }_B^2{\tau }_i+{(i-1)}^2{\sigma }_3^2]}}\exp \left[-\frac{{(x_{{\tau }_i^{-}}-\mu {\tau }_i-(i-1){\mu }_3)}^2}{2{\sigma }_B^2{\tau }_i+{(i-1)}^2{\sigma }_3^2}\right]\end{array}$$

(12)

where we let ${\tau }_i^{-}={\tau }_i$ for simplicity, but $x_{{\tau }_i^{-}}\ne x_{{\tau }_i}$. Then, we use $p(x_{{\tau }_i^{-}})$ to replace $g(x_{{\tau }_i^{-}})$ for deriving the lifetime estimation in Equation (11). In this case, by combing the results of Equations (7) and (11), we can obtain the approximate PDF of lifetime as follows,

$$\begin{array}{cc}\hfill f_T\left(t\right)=& \frac{1}{\sqrt{2\pi {\sigma }_B^2{t}^3}}\exp \left[-\frac{{(\xi -x_0-\mu t)}^2}{2{\sigma }_B^{2}t}\right],t\in (0,{\tau }_1)\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill f_T\left(t\right)\cong & {\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{\xi }p\left({\lambda }_1\right)p\left({\lambda }_3\right)p(x_{{\tau }_i^{-}})\frac{\xi -x_{{\tau }_i^{-}}-{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}+(t-{\tau }_i){\lambda }_2{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}-{\lambda }_3}{\sqrt{2\pi {\sigma }_B^2{(t-{\tau }_i)}^3}}\hfill \\ & \times \exp \left[-\frac{{(\xi -x_{{\tau }_i^{-}}-\mu (t-{\tau }_i)+{\lambda }_1{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}-{\lambda }_3)}^2}{2{\sigma }_B^2(t-{\tau }_i)}\right]d{x}_{{\tau }_i^{-}}d{\lambda }_{1}d{\lambda }_3,t\in [{\tau }_{i-1},{\tau }_i)or[{\tau }_{n_{\tau }},+\infty )\hfill \end{array}$$

(14)

where $i=2,3,\dots ,n_{\tau }$. In Equation (14), there are triple integrals needing to solve, which is similar to Equation (11) owing to three random variables. In order to simplify this integral, we introduce the following Theorem 1 based on the property of Gaussian distribution.

Theorem 1.

It is defined that $z_1\sim N({\mu }_{z_1},{\sigma }_{z_1})$ and $z_2\sim N({\mu }_{z_2},{\sigma }_{z_2})$ are two independent Gaussian random variables, and $A_1$, $A_2$, $B_1$, $B_2$, C, and D are fixed value. Then let $\mathbf{Z}=[z_1,z_2]$, we can have the following results,

$$\begin{array}{c}{\mathbb{E}}_{\mathbf{Z}}\left[\exp \left(-0.5A_1{z}_1^2-0.5A_2{z}_2^2+B_1{z}_1+B_2{z}_2+C{z}_1{z}_2-0.5D\right)\right]\hfill \\ =\frac{{\tilde{\sigma }}_{z_1}{\tilde{\sigma }}_{z_2}\sqrt{1-{\rho }^2}}{{\sigma }_{z_1}{\sigma }_{z_2}}\exp \left(\frac{A_1{\sigma }_{z_1}^2+1}{2{\sigma }_{z_1}^2}{\tilde{\mu }}_{z_1}^2+\frac{A_2{\sigma }_{z_2}^2+1}{2{\sigma }_{z_2}^2}{\tilde{\mu }}_{z_2}^2-C{\tilde{\mu }}_{z_1}{\tilde{\mu }}_{z_2}-0.5E\right)\hfill \\ {\mathbb{E}}_{\mathbf{Z}}\left[z_1\exp \left(-0.5A_1{z}_1^2-0.5A_2{z}_2^2+B_1{z}_1+B_2{z}_2+C{z}_1{z}_2-0.5D\right)\right]\hfill \\ =\frac{{\tilde{\sigma }}_{z_1}{\tilde{\sigma }}_{z_2}\sqrt{1-{\rho }^2}}{{\sigma }_{z_1}{\sigma }_{z_2}}{\tilde{\mu }}_{z_1}\exp \left(\frac{A_1{\sigma }_{z_1}^2+1}{2{\sigma }_{z_1}^2}{\tilde{\mu }}_{z_1}^2+\frac{A_2{\sigma }_{z_2}^2+1}{2{\sigma }_{z_2}^2}{\tilde{\mu }}_{z_2}^2-C{\tilde{\mu }}_{z_1}{\tilde{\mu }}_{z_2}-0.5E\right)\hfill \\ {\mathbb{E}}_{\mathbf{Z}}\left[z_2\exp \left(-0.5A_1{z}_1^2-0.5A_2{z}_2^2+B_1{z}_1+B_2{z}_2+C{z}_1{z}_2-0.5D\right)\right]\hfill \\ =\frac{{\tilde{\sigma }}_{z_1}{\tilde{\sigma }}_{z_2}\sqrt{1-{\rho }^2}}{{\sigma }_{z_1}{\sigma }_{z_2}}{\tilde{\mu }}_{z_2}\exp \left(\frac{A_1{\sigma }_{z_1}^2+1}{2{\sigma }_{z_1}^2}{\tilde{\mu }}_{z_1}^2+\frac{A_2{\sigma }_{z_2}^2+1}{2{\sigma }_{z_2}^2}{\tilde{\mu }}_{z_2}^2-C{\tilde{\mu }}_{z_1}{\tilde{\mu }}_{z_2}-0.5E\right)\hfill \\ {\mathbb{E}}_{\mathbf{Z}}\left[z_1{z}_2\exp \left(-0.5A_1{z}_1^2-0.5A_2{z}_2^2+B_1{z}_1+B_2{z}_2+C{z}_1{z}_2-0.5D\right)\right]\hfill \\ =\frac{{\tilde{\sigma }}_{z_1}{\tilde{\sigma }}_{z_2}\sqrt{1-{\rho }^2}}{{\sigma }_{z_1}{\sigma }_{z_2}}({\tilde{\mu }}_{z_1}{\tilde{\mu }}_{z_2}-\rho {\sigma }_{z_1}{\sigma }_{z_2})\exp \left(\frac{A_1{\sigma }_{z_1}^2+1}{2{\sigma }_{z_1}^2}{\tilde{\mu }}_{z_1}^2+\frac{A_2{\sigma }_{z_2}^2+1}{2{\sigma }_{z_2}^2}{\tilde{\mu }}_{z_2}^2-C{\tilde{\mu }}_{z_1}{\tilde{\mu }}_{z_2}-0.5E\right)\hfill \end{array}$$

(15)

where

$$\begin{array}{c}{\displaystyle {\tilde{\mu }}_{z_1}=\frac{(B_1{\sigma }_{z_1}^2+{\mu }_{z_1})(A_2{\sigma }_{z_2}^2+1)+(B_2{\sigma }_{z_2}^2+{\mu }_{z_2})C{\sigma }_{z_1}^2}{(A_1{\sigma }_{z_1}^2+1)(A_2{\sigma }_{z_2}^2+1)-C^2{\sigma }_{z_1}^2{\sigma }_{z_2}^2}}\hfill \\ {\displaystyle {\tilde{\mu }}_{z_2}=\frac{(B_2{\sigma }_{z_2}^2+{\mu }_{z_2})(A_1{\sigma }_{z_1}^2+1)+(B_1{\sigma }_{z_1}^2+{\mu }_{z_1})C{\sigma }_{z_2}^2}{(A_1{\sigma }_{z_1}^2+1)(A_2{\sigma }_{z_2}^2+1)-C^2{\sigma }_{z_1}^2{\sigma }_{z_2}^2}}\hfill \\ {\displaystyle {\rho }^2=\frac{C^2{\sigma }_{z_1}^2{\sigma }_{z_2}^2}{(A_1{\sigma }_{z_1}^2+1)(A_2{\sigma }_{z_2}^2+1)}}\hfill \\ {\displaystyle E=\frac{D{\sigma }_{z_1}^2{\sigma }_{z_2}^2+{\mu }_{z_1}^2{\sigma }_{z_2}^2+{\mu }_{z_2}^2{\sigma }_{z_1}^2}{{\sigma }_{z_2}^2{\sigma }_{z_1}^2}}\hfill \\ {\displaystyle {\tilde{\sigma }}_{z_1}{\tilde{\sigma }}_{z_2}=\frac{\rho }{C\sqrt{1-{\rho }^2}}}\hfill \end{array}$$

(16)

Proof. 

See Appendix A.

In this way, we can solve the integral with ${\lambda }_1$ and ${\lambda }_3$ in Equation (14) depending on the results of Theorem 1 and then Equation (14) can be rewritten as follows,

$$\begin{array}{cc}\hfill f_T\left(t\right)\cong & {\int }_{-\infty }^{\xi }\rho p(x_{{\tau }_i^{-}})\frac{\xi -x_{{\tau }_i^{-}}+{\tilde{\mu }}_1\left[(-1+{\lambda }_{2}t-{\tau }_i{\lambda }_2){\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}\right]-{\tilde{\mu }}_3}{C^{\prime }\sqrt{2\pi {\sigma }_B^2{(t-{\tau }_i)}^3}}\hfill \\ & \times \exp \left(\frac{A_1^{\prime }{\sigma }_1^2+1}{2{\sigma }_1^2}{\tilde{\mu }}_1^2+\frac{A_3^{\prime }{\sigma }_3^2+1}{2{\sigma }_3^2}{\tilde{\mu }}_3^2-C^{\prime }{\tilde{\mu }}_1{\tilde{\mu }}_3-0.5E^{\prime }\right)d{x}_{{\tau }_i^{-}},t\in [{\tau }_{i-1},{\tau }_i)or[{\tau }_{n_{\tau }},+\infty )\hfill \end{array}$$

(17)

where

$$\begin{array}{c}{\displaystyle {\tilde{\mu }}_1=\frac{(B_1^{\prime }{\sigma }_1^2+{\mu }_1)(A_3^{\prime }{\sigma }_3^2+1)+(B_3^{\prime }{\sigma }_3^2+{\mu }_3)C^{\prime }{\sigma }_1^2}{(A_1^{\prime }{\sigma }_1^2+1)(A_3^{\prime }{\sigma }_3^2+1)-C^{\prime 2}{\sigma }_1^2{\sigma }_3^2}}\hfill \\ {\displaystyle {\tilde{\mu }}_3=\frac{(B_3^{\prime }{\sigma }_3^2+{\mu }_3)(A_1^{\prime }{\sigma }_1^2+1)+(B_1^{\prime }{\sigma }_1^2+{\mu }_1)C^{\prime }{\sigma }_3^2}{(A_1^{\prime }{\sigma }_1^2+1)(A_3^{\prime }{\sigma }_3^2+1)-C^{\prime 2}{\sigma }_1^2{\sigma }_3^2}}\hfill \\ {\displaystyle {\rho }^{\prime 2}=\frac{C^{\prime 2}{\sigma }_1^2{\sigma }_3^2}{(A_1^{\prime }{\sigma }_1^2+1)(A_3^{\prime }{\sigma }_3^2+1)}}\hfill \\ {\displaystyle E^{\prime }=\frac{D^{\prime }{\sigma }_1^2{\sigma }_3^2+{\mu }_1^2{\sigma }_3^2+{\mu }_3^2{\sigma }_1^2}{{\sigma }_3^2{\sigma }_1^2}}\hfill \\ {\displaystyle A_1^{\prime }=\frac{{\mathrm{e}}^{-2{\lambda }_2(t-{\tau }_i)}}{{\sigma }_B^2(t-{\tau }_i)}}\hfill \\ {\displaystyle B_1^{\prime }=\frac{-{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}\left(\xi -x_{{\tau }_i^{-}}-\mu (t-{\tau }_i)\right)}{{\sigma }_B^2(t-{\tau }_i)}}\hfill \\ {\displaystyle A_3^{\prime }=\frac{1}{{\sigma }_B^2(t-{\tau }_i)}}\hfill \\ {\displaystyle B_3^{\prime }=\frac{\xi -x_{{\tau }_i^{-}}-\mu (t-{\tau }_i)}{{\sigma }_B^2(t-{\tau }_i)}}\hfill \\ {\displaystyle C^{\prime }=\frac{{\mathrm{e}}^{-{\lambda }_2(t-{\tau }_i)}}{{\sigma }_B^2(t-{\tau }_i)}}\hfill \\ {\displaystyle D^{\prime }=\frac{{\left[\xi -x_{{\tau }_i^{-}}-\mu (t-{\tau }_i)\right]}^2}{{\sigma }_B^2(t-{\tau }_i)}}\hfill \end{array}$$

(18)

However, it is not easy to obtain the analytical form of the above integrals. Fortunately, only univariate integral needs to be calculated, which can be solved by many numerical methods such as trapezoidal approximations, parabolas approximations, and Rhomberg integration.

It is noted that the time of the changing point is prearranged and known under the assumption, i.e., $N\left(t\right)$ is prearranged. In practice, the rest time may not be provided or known in advance, and it is unknown and random. In this case, we define the PDF of each changing point as $p\left({\tau }_i\right)$. Then, we can obtain the PDF of the lifetime based on the law of total probability.

$$\begin{array}{c}\hfill f_{RT}\left(t\right)=\int \int \dots \int f_T\left(t\right)p\left({\tau }_1\right)p\left({\tau }_2\right)\dots p\left({\tau }_{n_{\tau }}\right)d{\tau }_{1}d{\tau }_{2}d{\tau }_{n_{\tau }}\end{array}$$

(19)

where $f_T\left(t\right)$ denotes the PDF of the lifetime with fixed changing point. In this way, the results under the prearranged changing point can be extended to the random case. For example, Zhang et al. [25] utilized the semi-Markov model (SMM) to reflect the degradation phase switch, and then generated the distribution of each changing time. Owing to the limitation of space, we do not further investigate how to formulate the framework of mode transitions (i.e., the rest time) in this paper. ☐

Now, we have completed the lifetime estimation based on the proposed multi-phase degradation model. In order to facilitate the application of our approach, we should discuss how to identify the model based on the collected data.

4. Parameter Estimation Based on the ECM Algorithm

In this section, we mainly focus on the model identification. Firstly, we attempt to formulate the likelihood function based on the property of the Wiener process.

We define that $X=[x_0,x_1,\dots ,x_k]$ denotes the degradation data at time $[t_0,t_1,\dots ,t_k]$. For simplicity, we tranform $X=[x_0,x_1,\dots ,x_k]$ into $X_{0:k}=[x_{1,1},x_{1,2},\dots x_{1,N_1},x_{2,1},x_{2,1},\dots ,x_{2,N_2},$$\dots x_{i,j},\dots ,x_{n_{\tau },N_{n_{\tau }}}]$, where $x_{i,j}$ represents the j-th observation at i-th phase, and thus $k+1={\displaystyle \sum _{i=1}^{n_{\tau }}}{N}_i$.

It is assumed that ${\lambda }_1$ and ${\lambda }_3$ are fixed, then the increment of observation data can be written as,

$$\begin{array}{c}\hfill \Delta x_{i,j}=\left\{\begin{array}{cc}\mu \Delta t_{i,j}+{\sigma }_{B}B(\Delta t_{i,j})\hfill & i=1\hfill \\ \mu \Delta t_{i,j}-{\lambda }_1+{\lambda }_3+{\sigma }_{B}B(\Delta t_{i,j})\hfill & i=j,i\ne 1\hfill \\ \mu \Delta t_{i,j}-{\lambda }_2{\lambda }_1{\int }_{t_{i,j-1}}^{t_{i,j}}{e}^{-{\lambda }_2(\tau -t_i)}d\tau +{\sigma }_{B}B(\Delta t_{i,j})\hfill & i\ne j,i\ne 1\hfill \end{array}\right.\end{array}$$

(20)

where $i=1,2,\dots n_{\tau }$.

However, due to the uncertainty of ${\lambda }_1$ and ${\lambda }_3$, it is hard to formulate the likelihood function, and further the analytical solution of likelihood function cannot be obtained. As such, it is difficult to estimate the parameters via the traditional maximum likelihood estimation (MLE). In this case, it is natural to treat ${\lambda }_1$ and ${\lambda }_3$ as latent variables and adopt EM algorithm or its extended method for parameter estimation. It is well-known that two steps are included in the EM algorithm, i.e., E-step and M-step. Then we will introduce how to realize the model identification according to such two steps.

E-step: Let $[{\lambda }_1,{\lambda }_3]$ represent the latent variables. Then, if the latent variables are known, we can obtain the likelihood function as shown in Equation (21),

$$\begin{array}{cc}\hfill l(\Theta |{\mathbf{X}}_{0:k},{\mathbf{\lambda }}_{2:n_{\tau }})& ={\displaystyle \prod _{i=2}^{n_{\tau }}}{\displaystyle \prod _{j=2}^{N_i}}\frac{1}{\sqrt{2\pi {\sigma }_B^2\Delta t_{i,j}}}\exp \left[-\frac{{(\Delta x_{i,j}-\mu \Delta t_{i,j}-{\lambda }_2{\lambda }_1{\int }_{t_{i,j-1}}^{t_{i,j}}{e}^{-{\lambda }_2(\tau -t_i)}d\tau )}^2}{2{\sigma }_B^2\Delta t_{i,j}}\right]\hfill \\ & +{\displaystyle \prod _{i=2}^{n_{\tau }}}\frac{1}{\sqrt{2\pi {\sigma }_B^2\Delta t_{i,j}}}\exp \left[-\frac{{(x_{i,1}-x_{i-1,N_{i-1}}-\mu \Delta t_{i,j}+{\lambda }_1-{\lambda }_3)}^2}{2{\sigma }_B^2\Delta t_{i,j}}\right]+{\displaystyle \prod _{i=2}^{n_{\tau }}}\frac{1}{\sqrt{2\pi {\sigma }_1^2}}\exp \left[-\frac{{\left({\lambda }_1-{\mu }_1\right)}^2}{2{\sigma }_1^2}\right]\hfill \\ & +{\displaystyle \prod _{i=2}^{n_{\tau }}}\frac{1}{\sqrt{2\pi {\sigma }_3^2}}\exp \left[-\frac{{\left({\lambda }_3-{\mu }_1\right)}^2}{2{\sigma }_3^2}\right]+{\displaystyle \prod _{j=2}^{N_1}}\frac{1}{\sqrt{2\pi {\sigma }_B^2\Delta t_{i,j}}}\exp \left[-\frac{{\left(x_{1,j}-x_{1,j-1}-\mu \Delta t_{i,j}\right)}^2}{2{\sigma }_B^2\Delta t_{i,j}}\right]\hfill \end{array}$$

(21)

where $\Theta =[\mu ,{\sigma }_B,{\lambda }_2,{\mu }_1,{\mu }_3,{\sigma }_1,{\sigma }_3]$ denotes all parameters and ${\mathbf{\lambda }}_{2:n_{\tau }}$ is the observation of $[{\lambda }_1,{\lambda }_3]$. Next, we calculate the conditional expectation of complete-data likelihood function,

$$\begin{array}{c}Q(\Theta |{\widehat{\Theta }}_k^{\left(m\right)})={\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[\ln p({\mathbf{X}}_{0:k},{\mathbf{\lambda }}_{2:n_{\tau }}|\Theta )\right]\hfill \\ {\displaystyle ={\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[-{\displaystyle \sum _{i=2}^{n_{\tau }}}{\displaystyle \sum _{j=2}^{N_i}}\frac{{(\Delta x_{i,j}-\mu \Delta t_{i,j}+{\lambda }_{1,i}{e}^{-{\lambda }_2{t}_{i,j}}-{\lambda }_{1,i}{e}^{-{\lambda }_2{t}_{i,j-1}})}^2}{2{\sigma }_B^2\Delta t_{i,j}}\right.}\hfill \\ {\displaystyle -{\displaystyle \sum _{i=2}^{n_{\tau }}}\frac{{(x_{i,1}-x_{i-1,N_{i-1}}-\mu \Delta t_{i,j}+{\lambda }_{1,i}-{\lambda }_3)}^2}{2{\sigma }_B^2\Delta t_{i,j}}-{\displaystyle \sum _{j=2}^{N_1}}\frac{{(x_{1,j}-x_{1,j-1}-\mu \Delta t_{i,j})}^2}{2{\sigma }_B^2\Delta t_{i,j}}}\hfill \\ {\displaystyle \left.+{\displaystyle \sum _{i=2}^{n_{\tau }}}{N}_i\ln \frac{1}{\sqrt{2\pi {\sigma }_B^2\Delta t_{i,j}}}+{\displaystyle \sum _{i=2}^{n_{\tau }}}\ln \frac{1}{\sqrt{2\pi {\sigma }_1^2}}-{\displaystyle \sum _{i=2}^{n_{\tau }}}\frac{{({\lambda }_{1,i}-{\mu }_1)}^2}{2{\sigma }_1^2}+{\displaystyle \sum _{i=2}^{n_{\tau }}}\ln \frac{1}{\sqrt{2\pi {\sigma }_3^2}}-{\displaystyle \sum _{i=2}^{n_{\tau }}}\frac{{({\lambda }_{3,i}-{\mu }_3)}^2}{2{\sigma }^2}\right]}\hfill \end{array}$$

(22)

where ${\widehat{\Theta }}_k^{\left(m\right)}$ represents the all estimates in the m-th step based on ${\mathbf{X}}_{0:k}$.

It is noteworthy that ${\lambda }_1$ and ${\lambda }_3$ follow the Gaussian distribution and we only need to derive the expressions of ${\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{1,i}\right]$, ${\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{3,i}\right]$, ${\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{1,i}^2\right]$, ${\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{3,i}^2\right]$, and ${\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{1,i}{\lambda }_{3,i}\right]$. In practice, the interval time is usually defined as a fixed value, thus we let $\Delta t_{i,j}=\Delta t$ for simplicity. Then, based on the Bayesian rule, following results for deriving $Q(\Theta |{\widehat{\Theta }}_k^{\left(m\right)})$ can be obtained,

$$\begin{array}{c}{\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{1,i}\right]={\mu }_{{\lambda }_1},{\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{3,i}\right]={\mu }_{{\lambda }_3},{\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{1,i}^2\right]={\mu }_{{\lambda }_1}^2+{\sigma }_{{\lambda }_1}^2\hfill \\ {\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{3,i}^2\right]={\mu }_{{\lambda }_3}^2+{\sigma }_{{\lambda }_3}^2,{\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{1,i}{\lambda }_{3,i}\right]={\mu }_{{\lambda }_1}{\mu }_{{\lambda }_3}-\rho {\sigma }_{{\lambda }_1}{\sigma }_{{\lambda }_3}\hfill \\ {\mu }_{{\lambda }_1}=\frac{\left({{\widehat{\mu }}_1}^{\left(m\right)}{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t-{\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})(x_{i,j}-x_{i,j-1}-{\widehat{\mu }}^{\left(m\right)}\Delta t)-{\widehat{\sigma }}_1^{2,\left(m\right)}(x_{i,1}-x_{i-1,N_{i-1}}-{\widehat{\mu }}^{\left(m\right)}\Delta t)\right)\left({\widehat{\sigma }}_3^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)}{\left({\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}{(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}^2+{\widehat{\sigma }}_1^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)\left({\widehat{\sigma }}_3^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)-{\widehat{\sigma }}_1^{2,\left(m\right)}{\widehat{\sigma }}_3^{2,\left(m\right)}}\hfill \\ -\frac{\left({\widehat{\sigma }}_3^{2,\left(m\right)}(x_{i,1}-x_{i-1,N_{i-1}}-{\widehat{\mu }}^{\left(m\right)}\Delta t)+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t{{\widehat{\mu }}_3}^{\left(m\right)}\right)\left({\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}{(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}^2+{\widehat{\sigma }}_1^{2,\left(m\right)}\right)}{\left({\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}{(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}^2+{\widehat{\sigma }}_1^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)\left({\widehat{\sigma }}_3^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)-{\widehat{\sigma }}_1^{2,\left(m\right)}{\widehat{\sigma }}_3^{2,\left(m\right)}}\hfill \\ {\mu }_{{\lambda }_3}=\frac{\left({\widehat{\sigma }}_3^{2,\left(m\right)}(x_{i,1}-x_{i-1,N_{i-1}}-{\widehat{\mu }}^{\left(m\right)}\Delta t)+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t{{\widehat{\mu }}_3}^{\left(m\right)}\right)\left({\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}{(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}^2+{\widehat{\sigma }}_1^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)}{\left({\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}{(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}^2+{\widehat{\sigma }}_1^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)\left({\widehat{\sigma }}_3^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)-{\widehat{\sigma }}_1^{2,\left(m\right)}{\widehat{\sigma }}_3^{2,\left(m\right)}}\hfill \\ -\frac{\left({{\widehat{\mu }}_1}^{\left(m\right)}{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t-{\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})(x_{i,j}-x_{i,j-1}-{\widehat{\mu }}^{\left(m\right)}\Delta t)-{\widehat{\sigma }}_1^{2,\left(m\right)}(x_{i,1}-x_{i-1,N_{i-1}}-{\widehat{\mu }}^{\left(m\right)}\Delta t)\right){\widehat{\sigma }}_3^{2,\left(m\right)}}{\left({\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}{(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}^2+{\widehat{\sigma }}_1^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)\left({\widehat{\sigma }}_3^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)-{\widehat{\sigma }}_1^{2,\left(m\right)}{\widehat{\sigma }}_3^{2,\left(m\right)}}\hfill \\ {\sigma }_{{\lambda }_1}^2=\frac{\left({\widehat{\sigma }}_3^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right){\widehat{\sigma }}_1^{2,m}{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t}{\left({\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}{(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}^2+{\widehat{\sigma }}_1^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)\left({\widehat{\sigma }}_3^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)-{\widehat{\sigma }}_1^{2,\left(m\right)}{\widehat{\sigma }}_3^{2,\left(m\right)}}\hfill \\ {\sigma }_{{\lambda }_3}^2=\frac{\left({\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}{(e^{-{\widehat{\lambda }}_2^{\left(m\right)}t}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}^2+{\widehat{\sigma }}_1^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right){\widehat{\sigma }}_3^{2,m}{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t}{\left({\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}{(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}^2+{\widehat{\sigma }}_1^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)\left({\widehat{\sigma }}_3^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)-{\widehat{\sigma }}_1^{2,\left(m\right)}{\widehat{\sigma }}_3^{2,\left(m\right)}}\hfill \\ \rho =\frac{{\widehat{\sigma }}_1^{\left(m\right)}{\widehat{\sigma }}_3^{\left(m\right)}}{\sqrt{\left({\widehat{\sigma }}_1^{2,\left(m\right)}{\displaystyle \sum _{j=2}^{N_i}}{(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}^2+{\widehat{\sigma }}_1^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)\left({\widehat{\sigma }}_3^{2,\left(m\right)}+{\widehat{\sigma }}_B^{2,\left(m\right)}\Delta t\right)}}\hfill \end{array}$$

(23)

Proof. 

See Appendix B.

In this way, the expression of $Q(\Theta |{\widehat{\Theta }}_k^{\left(m\right)})$ has been attained. Then the next step is to maximize $Q(\Theta |{\widehat{\Theta }}_k^{\left(m\right)})$.

M-step: In order to maximize $Q(\Theta |{\widehat{\Theta }}_k^{\left(m\right)})$, the direct way is to make $\frac{\partial Q(\Theta |{\widehat{\Theta }}_k^{\left(m\right)})}{\partial \Theta }=0$ and then solve such the equation. In this way, we can obtain some solutions,

$$\begin{array}{c}{\widehat{\mu }}_1^{(m+1)}=\frac{{\displaystyle \sum _{i=2}^{n_{\tau }}}{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{1,i}\right]}{n_{\tau }-1}\hfill \\ {\widehat{\mu }}_3^{(m+1)}=\frac{{\displaystyle \sum _{i=2}^{n_{\tau }}}{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{3,i}\right]}{n_{\tau }-1}\hfill \\ {\widehat{\sigma }}_1^{2,(m+1)}=\frac{{\displaystyle \sum _i^N}{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{1,i}^2\right]-{\displaystyle \sum _i^N}{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}^2\left[{\lambda }_{1,i}\right]}{n_{\tau }-1}\hfill \\ {\widehat{\sigma }}_3^{2,(m+1)}=\frac{{\displaystyle \sum _i^N}{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{3,i}^2\right]-{\displaystyle \sum _i^N}{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}^2\left[{\lambda }_{3,i}\right]}{n_{\tau }-1}\hfill \end{array}$$

(24)

where the expressions of ${\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{1,i}\right]$, ${\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{3,i}\right]$, ${\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{1,i}^2\right]$, ${\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{3,i}^2\right]$, and ${\mathbb{E}}_{{\lambda }_1,{\lambda }_3\left|{\mathbf{X}}_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}\right.}\left[{\lambda }_{1,i}{\lambda }_{3,i}\right]$ can be found in Equation (23). It is noted that ${\widehat{\mu }}_1^{(m+1)}$, ${\widehat{\mu }}_3^{(m+1)}$, ${\widehat{\sigma }}_1^{(m+1)}$, and ${\widehat{\sigma }}_3^{(m+1)}$ are global optimal solutions for maximizing $Q(\Theta |{\widehat{\Theta }}_k^{\left(m\right)})$.

However, only ${\mu }_1$, ${\mu }_3$, ${\sigma }_1$, and ${\sigma }_3$ can be derived with an analytical forms, and other parameters i.e., μ, ${\sigma }_B$, and ${\lambda }_2$ cannot be attained owing to the complexity of $\frac{\partial Q(\Theta |{\widehat{\Theta }}_k^{\left(m\right)})}{\partial \Theta }=0$. If we choose some of the heuristic optimization methods to deal with it, not only is the existence and convergence of optimization for parameters estimating hard to analyze, but also the online capability will be poor. Under this consideration, we utilize the ECM algorithm to simplify the issue [32,33]. According to the ECM algorithm, we firstly fix ${\lambda }_2$ and then derive the results of μ and ${\sigma }_B$, i.e., we treat ${\lambda }_2^{\left(m\right)}$ as the real value of ${\lambda }_2$ in this step. In this way, we can obtain analytical solutions of μ and ${\sigma }_B$ as shown in follows,

$$\begin{array}{cc}\hfill {\widehat{\mu }}^{(m+1)}=& \frac{{\displaystyle \sum _{i=2}^{n_{\tau }}}{\displaystyle \sum _{j=2}^{N_i}}(x_{i,j}-x_{i,j-1})(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})+{\displaystyle \sum _{j=2}^{N_1}}(x_{1,j}-x_{1,j-1})}{\left({\displaystyle \sum _{i=1}^{n_{\tau }}}{N}_i-1\right)\Delta t}\hfill \\ & +\frac{{\displaystyle \sum _{i=2}^{n_{\tau }}}\left(x_{i,1}-x_{i-1,N_{i-1}}+{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{1,i}\right]-{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{3,i}\right]\right)}{\left({\displaystyle \sum _{i=1}^{n_{\tau }}}{N}_i-1\right)\Delta t}\hfill \\ & +\frac{{\displaystyle \sum _{i=2}^{n_{\tau }}}{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{1,i}\right]{\displaystyle \sum _{j=1}^{N_i}}(x_{i,j}-x_{i,j-1})(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}{\left({\displaystyle \sum _{i=1}^{n_{\tau }}}{N}_i-1\right)\Delta t}\hfill \end{array}$$

(25)

$$\begin{array}{c}{\widehat{\sigma }}_B^{2,(m+1)}=-\frac{{\displaystyle \sum _{i=1}^{n_{\tau }}}{\displaystyle \sum _{j=2}^{N_i}}{(x_{i,j}-x_{i,j-1})}^2+k{\widehat{\mu }}^{2,(m+1)}\Delta t+{\displaystyle \sum _{i=2}^{n_{\tau }}}{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{1,i}^2\right]\left[{\displaystyle \sum _{j=2}^{N_i}}{(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})}^2+1\right]}{\left({\displaystyle \sum _{i=1}^{n_{\tau }}}{N}_i-1\right)\Delta t}\hfill \\ +\frac{2{\displaystyle \sum _{i=2}^{n_{\tau }}}{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{1,i}\right]\left[{\displaystyle \sum _{j=2}^{N_i}}(x_{i,j}-x_{i,j-1})(e^{-{\lambda }_2^{\left(m\right)}{t}_{i,j}}-e^{-{\lambda }_2^{\left(m\right)}{t}_{i,j-1}})-{\widehat{\mu }}^{(m+1)}\Delta t-{\widehat{\lambda }}_3^{(m+1)}\right]-2{\displaystyle \sum _{i=2}^{n_{\tau }}}{\displaystyle \sum _{j=2}^{N_i}}(x_{i,j}-x_{i,j-1}){\widehat{\mu }}^{(m+1)}\Delta t}{\left({\displaystyle \sum _{i=1}^{n_{\tau }}}{N}_i-1\right)\Delta t}\hfill \\ -\frac{2{\widehat{\mu }}^{(m+1)}\Delta t{\displaystyle \sum _{i=2}^{n_{\tau }}}{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{1,i}\right]{\displaystyle \sum _{j=2}^{N_i}}(e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j}}-e^{-{\widehat{\lambda }}_2^{\left(m\right)}{t}_{i,j-1}})+2{\widehat{\mu }}^{(m+1)}\Delta t{\displaystyle \sum _{j=2}^{N_1}}(x_{1,j}-x_{1,j-1})}{\left({\displaystyle \sum _{i=1}^{n_{\tau }}}{N}_i-1\right)\Delta t}\hfill \\ +\frac{{\displaystyle \sum _{i=2}^{n_{\tau }}}{\left(x_{i,1}-x_{i-1,N_{i-1}}\right)}^2+2{\displaystyle \sum _{i=2}^{n_{\tau }}}\left(x_{i,1}-x_{i-1,N_{i-1}}\right)\left({\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{1,i}\right]-{\widehat{\lambda }}_3^{(m+1)}-{\widehat{\mu }}^{(m+1)}\Delta t\right)+2N{\widehat{\lambda }}_3^{(m+1)}{\widehat{\mu }}^{(m+1)}\Delta t}{\left({\displaystyle \sum _{i=1}^{n_{\tau }}}{N}_i-1\right)\Delta t}\hfill \end{array}$$

(26)

where $k={\displaystyle \sum _{i=1}^{n_{\tau }}}{N}_i-1$.

Then next step is to derive ${\widehat{\lambda }}_2^{(m+1)}$ via maximizing $Q({\widehat{\lambda }}_2|{\widehat{\mu }}^{(m+1)},{\widehat{\sigma }}_B^{2,(m+1)},{\widehat{\lambda }}_3^{(m+1)},{\widehat{\mu }}_1^{(m+1)},{\widehat{\sigma }}_1^{2,(m+1)},{\widehat{\mu }}_3^{(m+1)},{\widehat{\sigma }}_3^{2,(m+1)})$, which can be formulated as,

$$\begin{array}{c}{\widehat{\lambda }}_2^{(m+1)}=\underset{{\lambda }_2}{\arg \max }{\mathbb{E}}_{{\lambda }_1,{\lambda }_3|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[\ln p(X_{0:k},{\lambda }_1,{\lambda }_3|{\widehat{\Theta }}_k^{(m+1)})\right]\hfill \\ =\underset{{\lambda }_2}{\arg \min }\left\{{\displaystyle \sum _{i=2}^{n_{\tau }}}{\displaystyle \sum _{j=2}^{N_i}}{\mathbb{E}}_{{\lambda }_{1,i}|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{1,i}^2\right]{\left(e^{-{\lambda }_2{t}_{i,j}}-e^{-{\lambda }_2{t}_{i,j-1}}\right)}^2-2{\widehat{\mu }}^{(m+1)}\Delta t{\displaystyle \sum _{i=2}^{n_{\tau }}}{\displaystyle \sum _{j=2}^{N_i}}(x_{i,j}-x_{i,j-1})\right.+\hfill \\ \left.2{\displaystyle \sum _{i=2}^{n_{\tau }}}\left({\mathbb{E}}_{{\lambda }_{1,i}|X_{0:k},{\widehat{\Theta }}_k^{\left(m\right)}}\left[{\lambda }_{1,i}\right]\right){\displaystyle \sum _{j=2}^{N_i}}\left[\left(e^{-{\lambda }_2{t}_{i,j}}-e^{-{\lambda }_2{t}_{i,j-1}}\right)\left(x_{i,j}-x_{i,j-1}-{\widehat{\mu }}^{(m+1)}\Delta t\right)\right]+{\displaystyle \sum _{i=2}^{n_{\tau }}}{\displaystyle \sum _{j=2}^{N_i}}\left({\widehat{\mu }}^{2,(m+1)}\Delta t^2+\Delta x_{i,j}^2\right)\right\}\hfill \end{array}$$

(27)

In this way, compared with the traditional EM algorithm, ECM algorithm can reduce the number of parameters for optimization from 4 to in every M-step, which decreases the computing complexity and save the time. ☐

4.1. Implementation Procedure

In order to make the present results more feasible for engineering applications, a step-by-step procedures of the proposed approach with respect to model identification are developed in this subsection and summarized as shown in

Table 1. The implementation procedures of model identification.

Algorithm Procedure:
Step 1.	Collect the degradation data ${\mathbf{X}}_{0:k}$, and then obtain the occurrence number of rest time, i.e., $n_{\tau }$;
Step 2.	Transform ${\mathbf{X}}_{0:k}$ into $X_{0:k}=[x_{1,1},x_{1,2},\dots x_{1,N_1},x_{2,1},x_{2,1},\dots ,x_{2,N_2},\dots x_{i,j},\dots ,x_{n_{\tau },N_{n_{\tau }}}]$ according to $n_{\tau }$, and then obtain the difference of total observed data $\Delta {\mathbf{X}}_{i,j}$, where $x_{i,j}$ represents the j-th observation at i-th phase;
Step 3.	Regard ${\lambda }_1$ and ${\lambda }_3$ as the latent variables, and formulate the complete-data likelihood as shown in Equation (21). Let $m=0$, and give the initial value ${\widehat{\Theta }}_k^{\left(m\right)}$.;
Step 4.	Calculate the conditional expectation of Equation (21), and then attain $Q(\Theta |{\widehat{\Theta }}_k^{\left(m\right)})$ as shown in Equation (22), where ${\widehat{\Theta }}_k^{\left(m\right)}$ denotes the estimates of all parameters at m-th iteration;
Step 5.	Fix ${\lambda }_2={\lambda }_2^{\left(m\right)}$, and obtain the estimates of other parameters via maximizing $Q(\mathbf{\theta }|{\widehat{\mathbf{\theta }}}_k^{\left(m\right)},{\lambda }_2^{\left(m\right)})$, where $\mathbf{\theta }$ denotes all parameters except ${\lambda }_2$. Then the results ${\widehat{\mathbf{\theta }}}_k^{(m+1)}$ can be found in Equations (24)–(26);
Step 6.	Fix $\mathbf{\theta }={\mathbf{\theta }}^{\left(m\right)}$, and derive ${\lambda }_2^{\left(m\right)}$ via maximizing $Q({\lambda }_2|{\widehat{\mathbf{\theta }}}_k^{(m+1)},{\lambda }_2^{\left(m\right)})$, which can be found in Equation (27);
Step 7.	Let $m=m+1$, and repeat Step 4 to Step 6 until the estimates ${\widehat{\Theta }}_k^{\left(m\right)}$ becomes convergence. Then such ${\widehat{\Theta }}_k^{\left(m\right)}$ can be treated as the final estimates of $\Theta$.

.

Following the above procedures, the proposed method can be established for model identification based on ECM algorithm.

5. Case Study

In this section, two examples are provided: (1) a numerical simulation is adopted to verify the accuracy of parameter estimation and the PDF of RUL; (2) The actual degradation data of battery is used to illustrate the feasibility of the proposed model.

5.1. Numerical Example

In this subsection, we concentrate on how to verify the reasonability and effectiveness of our theory, including the result of the approximate analytical lifetime estimation and the approach of parameter identification. Firstly, we will illustrate the method of lifetime estimation via comparing our results with those from Markov Chain Monte Carlo (MCMC). In this paper, two cases are taken into account: the fixed jump at the changing point and the random jump at the changing point. For the first case, we let $\mu =0.01$, ${\sigma }_B=0.1$, ${\lambda }_1=-5$, ${\lambda }_3=1$, and ${\lambda }_3=-0.02$. For another case, we let $\mu =0.01$, ${\sigma }_B=0.1$, ${\mu }_1=-5$, ${\mu }_3=0$, ${\sigma }_1=3$, ${\sigma }_3=1$, and ${\lambda }_2=-0.02$. According to the given parameters, we can further generate the degradation trajectories as shown in following Figure 2a,b. It is assumed that the failure threshold ξ is set at 60. It is interesting to be noted that if we make $y\left(t\right)=\xi -x\left(t\right)$, the $y\left(t\right)$ is similar to the practical degradation data as shown in Figure 1, where $x\left(t\right)$ denotes degradation path we generated based on the proposed degradation model in Equation (3). In this way, the degradation can be transformed into the degradation process with initial value $y_0=60$ and threshold $\xi =0$, and its degradation rate become negative. What should be noticed that such the transformation does affect the lifetime estimation under the concept of the FPT.

In addition, we adopt the MCMC to generate 1,000,000 sets of degradation trajectories based on our proposed model as shown in Equation (4) and collect their FPTs as the result of lifetime. Here these FPTs are regarded as the lifetime and then they will be compared with our theoretical results for illustration. In this way, we can obtain the results of our method and the MCMC separately, and the following Figure 3 shows the comparisons of the two aforementioned cases. The blue line denotes the results of the MCMC, and the red lines represent the results of our approach, and the green dotted lines are the results of the traditional way that ignores the influence of the regeneration. From the comparison as shown in Figure 3, we can notice that the results of our method are similar to those of the MCMC. It is interesting to be noteworthy that the deviations of lifetime estimation with fixed regeneration (or jump) are smaller than those with random regeneration owing to the uncertainty and randomness of ${\lambda }_1$ and ${\lambda }_3$. In addition, we can find that the deviation of the traditional method is obvious, especially the estimated PDFs at the changing points. Thus, it could be concluded that our method can do lifetime estimation for the proposed degradation model under the concept of the FPT efficiently.

Next, we will introduce how to realize model identification based on our algorithm. According to the proposed method in Section 4, we generate 10 degradation trajectories with 10 times random regeneration phenomena, where the parameters are set as those in the above case 2 and the each degradation phase lasts 1000 time steps. In this case, all data can be converted to 100 phases. Based on the proposed approach, we can attain the parameters’ estimates as following table shown.

From

Table 2. The parameters estimation with different sample size.

	Sample Size	$\mathit{\mu }$	${\mathit{\sigma }}_{\mathit{B}}$	${\mathit{\mu }}_1$	${\mathit{\mu }}_3$	${\mathit{\sigma }}_1$	${\mathit{\sigma }}_3$	${\mathit{\lambda }}_2$
2	$n=2$	0.0205	0.149	4.541	−0.289	2.898	1.491	0.0204
3	$n=5$	0.0148	0.072	4.516	−0.214	2.720	1.428	0.0210
4	$n=10$	0.0101	0.095	4.987	0.261	2.789	1.342	0.0196
5	True value	0.0100	0.100	5.000	0.000	3.000	1.000	0.0200

, we find that our results approach the true value, which verifies the effectiveness of our method. It is worth mentioning that the initial value of all parameters are set as $\mu =1$, ${\sigma }_B=5$, ${\mu }_1=1$, ${\mu }_3=4$, ${\sigma }_1=0.1$, ${\sigma }_3=10$, and ${\lambda }_2=-0.1$. To better illustrate, we display each iteration of parameter estimation based on ECM algorithm as follows.

It could be found that the estimates of the all parameters can converge to the estimated value quickly with around 10 steps of iteration in Figure 4. It means that the online capability of the proposed method is good and acceptable.

Therefore, the numerical example can illustrate our approach in theory. Next we will apply our method into the practical case for showing its practical application.

5.2. Practical Example

In this case, we choose the testing data of Li-Ion battery collected by the Center for Advanced Life Cycle Engineering (CALCE) of Maryland University to verify our approach [3,34]. Here, we choose the CS2 battery to verify our method. It is noted that such the battery is prismatic and its cathode is LiCoO₂. Its constant current rate is 0.5 C until the voltage reaches 4.2 V and then 4.2 V is sustained until the charging current drops to below 0.05 A. To better illustrate this, a set of degradation data is chosen to identify the model i.e., CS2-34, and its estimated parameters are provided for RUL estimation. According to the proposed method for model identification, the estimates of the all parameters are obtained as $\mu =-4.393\times {10}^{-04}$, ${\sigma }_B=0.0032$, ${\mu }_1=-0.0354$, ${\mu }_3=-0.0158$, ${\sigma }_1=0.0181$, ${\sigma }_3=0.0089$, and ${\lambda }_2=0.0812$. From the parameters’ estimates, it is noted that $-{\mu }_1+{\mu }_{3}0$ and it obviously larger than $\mu \Delta t$ and the increment of the degradation data. That is to say, the regeneration phenomenon does exist in the degradation process, and the testing rest is a non-negligible factor of the regeneration phenomenon. Moreover, ${\lambda }_{2}0$ means that the degradation rate will suddenly increase and then gradually recover.

Next, based on the parameters’ estimates, we try to illustrate the RUL estimation based on the proposed method. It is well-known that a certain percentage of the rated capacity is treated as the soft failure threshold of the battery. In this paper, we set the failure threshold at $70\%$ of the rated capacity to better illustrate the effect caused by the regeneration phenomena, i.e., the failure threshold $\xi =0.8$. Furthermore, what should be noticed is that the rest time of this degradation process is known. In another word, the changing time has been prearranged. In this way, combining the prior value of parameters and the failure threshold, we can obtain the PDFs of RUL for CS2-34 as shown in following Figure 5. What should be noticed is that the estimated RUL is a random distribution rather than a fixed value. So we choose the mean square error (MSE) to reflect the error as shown in Figure 5b.

From Figure 5, we can find that compared to the traditional method the results of our method can approach the true RUL with smaller estimated bias, since we take full consideration of the influence of such the regeneration phenomena. It is noted that if the regeneration phenomena are ignored, the estimated RUL will be influenced by the random jumps heavily, and the result will be overestimated owing to the state recovery, i.e., the estimated RUL become longer. In contrast, because our method has fully considered the effects of the regeneration phenomena on both degradation state and rate, the results of our method could be less affected. In order to better illustrate, we compare the PDFs of our method and the traditional method at the beginning and end of a degradation phase accordingly. The following Figure 6 shows that the PDFs of estimated RUL at cycle time 568 and 569.

It is noticed that the estimated bias between our result and traditional method at the cycle time 568 is smaller than cycle time 569. That is to say, the result of the traditional method may have much more bias at the beginning of the degradation phase since it is susceptible to the regeneration phenomena. Therefore, it can be concluded that the regeneration will influence the lifetime and RUL estimation, and the traditional method cannot deal with it well. On contrary, our method can not only reflect the degradation trajectory but also achieve more accurate estimated result, which illustrates the advantage and effectiveness of our approach.

6. Conclusions

In this paper, we mainly concentrate on how to model the degradation process with state-recovery phenomena. Under this consideration, we propose a multi-phase degradation with random jumps to describe such the degradation trajectory. In the proposed model, we classify the degradation process into several phases according to the rest time, and take a full account of the uncertainty of regeneration phenomena. Then we develop a model identification method based on the ECM algorithm to deal with complex likelihood function and the random latent variables. Furthermore, according to the proposed degradation model, we derive the lifetime estimation based on the time-scale transformation and law of total probability, and then obtain an approximate solution with the form of an single integral. To better illustrate our method, both numerical example and the practical example of CALCE batteries are adopted for demonstration.

Although the proposed method can better describe the degradation with regeneration phenomena and provide accurate lifetime estimation, there are still some problems needing to be investigated in the future. First, in this paper, we assume the rest time is prearranged, but the appearance of the rest time may be random and uncertain in practice. As such, in future work, we will try to formulate a framework of random operating state switches (i.e., the rest time), and then extended our approach for lifetime or RUL estimation to the stochastic case. Second, the changing degradation rate caused by the regeneration phenomena is a fixed value in our model. In fact, the changing degradation rate (i.e., the degradation rate at every phase) should exist difference between different degradation phases. Maybe, the random rate which can describe the phase-to-phase variability is more suitable. Third, it is noteworthy that the environmental temperature of the testing data we adopted does not change heavily so that we ignore its influence in this paper. However, the ambient temperature often change constantly in practice, which will affect the batteries’ degradation rate and fluctuation. We will continue to investigate such these issues in future work.