Heat Transfer Characteristics and Prediction Model of Supercritical Carbon Dioxide (SC-CO2) in a Vertical Tube
Abstract
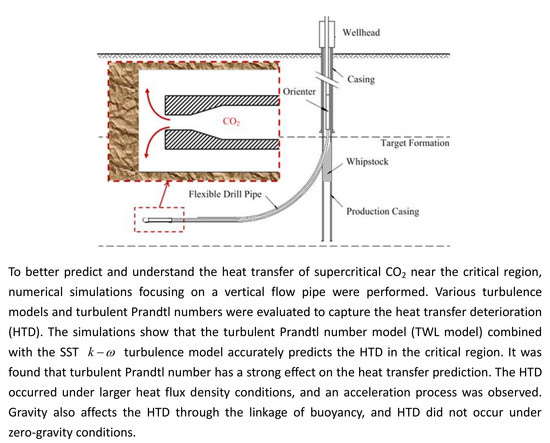
:1. Introduction
2. Numerical Methods
2.1. Real Gas Model
2.2. Governing Equations
2.3. Turbulent Model
2.3.1. Standard k-ε Turbulent Model
2.3.2. Realizable k-ε Turbulent Model
2.3.3. SST k-ω Turbulent Model
2.4. Variable Turbulent Prandtl Number Model
3. Numerical Simulation Setup
3.1. GeometryModel
3.2. Grid Independence Tests
3.3. Boundary Conditions
4. Results and Discussion
4.1. Model Verification
4.2. HTD Mechanism and Prt Effects in the Simulation
4.2.1. Effects of Pr on the Axial Velocity
4.2.2. Effects of Pr on the Density
4.2.3. Effects of Pr on the Turbulent Kinetic Energy
4.2.4. Effects of the Pr on the Turbulent Viscosity
4.3. Effects of Heat Flux on Heat Transfer
4.3.1. HTD Identification
4.3.2. Effects of Heat Flux on HTD
4.4. Effects of Gravity on Heat Transfer Near the Critical Point
4.4.1. Effects of Gravity on the Axial Velocity
4.4.2. Effects of Gravity on the Turbulent Kinetic Energy
4.4.3. Effects of Gravity on the Turbulent Viscosity
5. Conclusions
- (1)
- A better prediction of the tube wall temperature can be achieved with the variable Prt model combined with the SST k-ω model, especially for the HTD cases.
- (2)
- The Turbulent Prandtl number (Prt) plays an important role in predicting the heat transfer, and a larger Prt value decreases the turbulent mixing contribution to the heat transfer.
- (3)
- The HTD occurred under larger heat flux density conditions. An ‘‘M”-shaped velocity profile was observed when HTD occurred, indicating an acceleration process occurring in the heat transfer process. The peak value of the turbulent kinetic energy was observed in the near wall region, and it decreased quickly in the mainstream direction. In this case, the turbulent viscosity decreased and the turbulent flow tended to become laminar. When the heat crisis was weakened, the variation in the velocity and turbulent kinetic energy near the wall became smooth, and the turbulent viscosity began to increase.
- (4)
- Gravity affects the HTD through the linkage of buoyancy, and HTD did not occur under zero-gravity conditions.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclatures
| Symbol | Description |
| A, B, C, D, i, j, k | Serial number |
| A | Specific Helmholtz energy |
| B | Second virial coefficient |
| p | Pressure |
| Mass density, kg/m3 | |
| T | Temperature, K |
| Normalized density, | |
| a,b,d,n,t | Adjustable parameters |
| Adjustable parameters | |
| Functions | |
| Inverse reduced temperature, | |
| Tc | Supercritical temperature, K |
| h | Specific enthalpy, J |
| Ui, Uj | Velocity components in Cartesian coordinates, (i, j = 1, 2, 3) |
| xi, xj | Location in Cartesian coordinates, m |
| fi | Body force component in Cartesian coordinates |
| μ | Dynamic viscosity |
| μt | Turbulent dynamic viscosity |
| Pr | Prandtl Number |
| Prt | Turbulent Prandtl Number |
| w | Speed of sound |
| Partial differential | |
| ,, | Constant parameter in standard k-ε Turbulent Model |
| Variance | |
| G | Turbulent kinetic energy |
| Superscripts | Description |
| o | Ideal Gas property |
| r | Residual |
| Subscripts | Description |
| t | Turbulent |
| s | Denotes the vapor presssure |
| i,j,k | Indices |
References
- EIA, The U.S. Energy Information Administration. Shale Gas Production. Available online: https://www.eia.gov/dnav/ng/ng_prod_shalegas_s1_a.htm (accessed on 14 December 2016).
- Fallahzadeh, S.; Fallahzadeh, S.H.; Hossain, M.M.; James Cornwell, A.; Rasouli, V. Near Wellbore Hydraulic Fracture Propagation from Perforations in Tight Rocks: The Roles of Fracturing Fluid Viscosity and Injection Rate. Energies 2017, 10, 359. [Google Scholar] [CrossRef]
- Gale, J.F.W.; Reed, R.M.; Holder, J. Natural fractures in the Barnett Shale and their importance for hydraulic fracture treatments. AAPG Bull. 2007, 91, 603–622. [Google Scholar] [CrossRef]
- Kasza, P.; Wilk, K. Completion of shale gas formations by hydraulic fracturing. Przem. Chem. 2012, 91, 608–612. [Google Scholar]
- Gregory, K.B.; Vidic, R.D.; Dzombak, D.A. Water Management Challenges Associated with the Production of Shale Gas by Hydraulic Fracturing. Elements 2011, 7, 181–186. [Google Scholar] [CrossRef]
- Barati, R. Application of nanoparticles as fluid loss control additives for hydraulic fracturing of tight and ultra-tight hydrocarbon-bearing formations. J. Nat. Gas Sci. Eng. 2015, 27, 1321–1327. [Google Scholar] [CrossRef]
- Vengosh, A.; Jackson, R.B.; Warner, N.; Darrah, T.H.; Kondash, A. A critical review of the risks to water resources from unconventional shale gas development and hydraulic fracturing in the United States. Environ. Sci. Technol. 2014, 48, 8334–8348. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, G.M.; Eaton, D.W.; Ghofrani, H.; Walker, D.; Cheadle, B.; Schultz, R.; Shcherbakov, R.; Tiampo, K.; Gu, J.; Harrington, R.M.; et al. Hydraulic fracturing and seismicity in the western Canada sedimentary basin. Seismol. Res. Lett. 2016, 87, 631–647. [Google Scholar] [CrossRef]
- Clarke, H.; Eisner, L.; Styles, P.; Turner, P. Felt seismicity associated with shale gas hydraulic fracturing: The first documented example in Europe. Geophys. Res. Lett. 2015, 41, 8308–8314. [Google Scholar] [CrossRef]
- Skoumal, R.; Brudzinski, M.R.; Currie, B.S. Earthquakes Induced by Hydraulic Fracturing in Poland Township, Ohio. Bull. Seismol. Soc. Am. 2015, 105, 189–197. [Google Scholar] [CrossRef]
- Jackson, R.B.; Vengosh, A.; Darrah, T.H.; Warner, N.R.; Down, A. Shale Gas, Hydraulic Fracturing, and Environmental Health: An Overview. Environ. Mol. Mutag. 2013, 54, S13. [Google Scholar]
- Kolle, J.J. Coiled-Tubing Drilling with Supercritical Carbon Dioxide. In Proceedings of the SPE/CIM International Conference on Horizontal Well Technology, Calgary, AL, Canada, 6–8 November 2000. [Google Scholar]
- Jacob, F.; Rolt, A.M.; Sebastiampillai, J.M.; Sethi, V.; Belmonte, M.; Cobas, P. Performance of a Supercritical CO2 Bottoming Cycle for Aero Applications. Appl. Sci. 2017, 7, 255. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, D.; Zhang, D.; Xie, Y. Investigation on Unsteady Flow Characteristics of a SCO2 Centrifugal Compressor. Appl. Sci. 2017, 7, 310. [Google Scholar] [CrossRef]
- Hu, Y.; Kang, Y.; Wang, X.; Li, X.; Huang, M.; Zhang, M. Experimental and theoretical analysis of a supercritical carbon dioxide jet on wellbore temperature and pressure. J. Nat. Gas Sci. Eng. 2016, 36, 108–116. [Google Scholar] [CrossRef]
- Huang, M.; Kang, Y.; Long, X.; Wang, X.; Hu, Y.; Li, D.; Zhang, M. Effects of a Nano-Silica Additive on the Rock Erosion Characteristics of a SC-CO2 Jet under Various Operating Conditions. Appl. Sci. 2017, 7, 153. [Google Scholar] [CrossRef]
- Huang, M.; Kang, Y.; Wang, X.; Hu, Y.; Li, D.; Cai, C.; Chen, F. Effects of Nozzle Configuration on Rock Erosion Under a Supercritical Carbon Dioxide Jet at Various Pressures and Temperatures. Appl.Sci. 2017, 7, 606. [Google Scholar] [CrossRef]
- Li, M.; Ni, H.; Wang, R.; Xiao, C. Comparative simulation research on the stress characteristics of supercritical carbon dioxide jets, nitrogen jets and water jets. Eng. Appl. Comput. Fluid Mech. 2017, 11, 357–370. [Google Scholar] [CrossRef]
- Tian, S.C.; Zhang, Q.L.; Li, G.S.; Chi, H.P.; Wang, H.Z.; Peng, K.W.; Li, Z.K. Rock-Breaking Characteristics for the Combined Swirling and Straight Supercritical Carbon Dioxide Jet under Ambient Pressure. At. Sprays 2016, 26, 659–671. [Google Scholar] [CrossRef]
- Wang, H.; Li, G.; He, Z.; Shen, Z.; Wang, M.; Wang, Y. Mechanism study on rock breaking with supercritical carbon dioxide jet. At. Sprays 2017, 27, 383–394. [Google Scholar] [CrossRef]
- Middleton, R.S.; Carey, J.W.; Currier, R.P.; Hyman, J.D.; Kang, Q.; Karra, S.; Jiménez-Martínez, J.; Porter, M.L.; Viswanathan, S. Shale gas and non-aqueous fracturing fluids: Opportunities and challenges for supercritical CO 2. Appl. Energy 2015, 147, 500–509. [Google Scholar] [CrossRef]
- Cheng, X.; Schulenberg, T. Heat Transfer at Supercritical Pressures—Literature Review and Application to an HPLWR; Energietechnik: Berlin, Germany, 2001; ISBN 0947-8620. [Google Scholar]
- Pioro, I.L.; Duffey, R.B. Experimental heat transfer in supercritical water flowing inside channels (survey). Nucl. Eng. Des. 2005, 235, 2407–2430. [Google Scholar] [CrossRef]
- Pan, M.; Bulatov, I.; Smith, R.; Kim, J.K. Novel MILP-based iterative method for the retrofit of heat exchanger networks with intensified heat transfer. Comput. Chem. Eng. 2012, 42, 263–276. [Google Scholar] [CrossRef]
- Kirillov, P.L. Heat-transfer crisis in channels. At. Energy 1996, 80, 348–357. [Google Scholar] [CrossRef]
- Pavlenko, A.N.; Chekhovich, V.Y. Heat transfer crisis at transient heat release. Russ. J. Eng. Thermophys. 1991, 1, 73–92. [Google Scholar]
- Wood, R.D.; Smith, J.M. Heat transfer in the critical region-temperature and velocity profiles in turbulent flow. AIChE J. 1964, 10, 180–186. [Google Scholar] [CrossRef]
- Shiralkar, B.S.; Griffith, P. Deterioration in heat transfer to fluids at supercritical pressure and high heat fluxes. J. Heat Transf. 1968, 91, 67. [Google Scholar] [CrossRef]
- Adebiyi, G.A.; Hall, W.B. Experimental investigation of heat transfer to supercritical pressure carbon dioxide in a horizontal pipe. Int. J. Heat Mass Transf. 1976, 19, 715–720. [Google Scholar] [CrossRef]
- Gungor, K.E.; Winterton, R.H.S. A general correlation for flow boiling in tubes and annuli. Int. J. Heat Mass Transf. 1986, 29, 351–358. [Google Scholar] [CrossRef]
- Polyakov, A.F. Heat Transfer under Supercritical Pressures. Adv. Heat Transf. 1991, 21, 1–53. [Google Scholar] [CrossRef]
- Liao, S.M.; Zhao, T.S. A numerical investigation of laminar convection of supercritical carbon dioxide in vertical mini/micro tubes. Prog. Comput. Fluid Dyn. Int. J. 2002, 2, 144–152. [Google Scholar] [CrossRef]
- Yoon, S.H.; Kim, J.H.; Hwang, Y.W.; Kim, M.S.; Min, K.; Kim, Y. Heat transfer and pressure drop characteristics during the in-tube cooling process of carbon dioxide in the supercritical region. Int. J. Refrig. 2003, 26, 857–864. [Google Scholar] [CrossRef]
- Kim, J.K.; Hong, K.J.; Lee, J.S. Wall temperature measurement and heat transfer correlation of turbulent supercritical carbon dioxide flow in vertical circular/non-circular tubes. Nucl, Eng. Des. 2007, 237, 1795–1802. [Google Scholar] [CrossRef]
- Du, Z.; Lin, W.; Gu, A. Numerical investigation of cooling heat transfer to supercritical CO2 in a horizontal circular tube. J. Supercrit. Fluids 2010, 55, 116–121. [Google Scholar] [CrossRef]
- Yang, C.; Xu, J.; Wang, X.; Zhang, W. Mixed convective flow and heat transfer of supercritical CO2 in circular tubes at various inclination angles. Int. J. Heat Mass Transf. 2013, 64, 212–223. [Google Scholar] [CrossRef]
- Peeters, J.W.R.; T'Joen, C.; Rohde, M. Investigation of the thermal development length in annular upward heated laminar supercritical fluid flows. Int. J. Heat Mass Transf. 2013, 61, 667–674. [Google Scholar] [CrossRef]
- Koshizuka, S.; Takano, N.; Oka, Y. Numerical analysis of deterioration phenomena in heat transfer to supercritical water. Trans. Jpn. Soc. Mech. Eng. 1994, 60, 3077–3084. [Google Scholar] [CrossRef]
- Grabezhnaya, V.A.; Kirillov, P.L. Heat transfer under supercritical pressures and heat transfer deterioration boundaries. Therm. Eng. 2006, 53, 296–301. [Google Scholar] [CrossRef]
- Urbano, A.; Nasuti, F. Onset of Heat Transfer Deterioration in Supercritical Methane Flow Channels. J. Thermophys. Heat Transf. 2013, 27, 298. [Google Scholar] [CrossRef]
- Wen, Q.L.; Gu, H.Y. Numerical simulation of heat transfer deterioration phenomenon in supercritical water through vertical tube. Ann. Nuclear Energy 2010, 37, 1272–1280. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-Point Temperature to 1100 K at Pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Von Helmholtz, H. Physical Memoirs Selected and Translated from Foreign Sources; Taylor & Francis: London, UK, 1882. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: New York, NY, USA, 1972; ISBN 9780124380509. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-[epsilon] eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Kays, W.M. Turbulent Prandtl number. Where are we? J. Heat Transf. 1994, 116, 284–295. [Google Scholar] [CrossRef]
- Tang, G.; Shi, H.; Wu, Y.; Lu, J.; Li, Z.; Liu, Q.; Zhang, H. A variable turbulent Prandtl number model for simulating supercritical pressure CO2 heat transfer. Int. J. Heat Mass Transf. 2016, 102, 1082–1092. [Google Scholar] [CrossRef]
- Weinberg, R.S. Experimental and Theoretical Study of Buoyancy Effects in Forced Convection to Supercritical Pressure Carbon Dioxide; University of Manchester: Manchester, UK, 1972. [Google Scholar]
- Jackson, J.D.; Hall, W.B. Influences of buoyancy on heat transfer to fluids flowing in vertical tubes under turbulent conditions. Turbul. Forced Convect. Channels Bundles 1979, 2, 613–640. [Google Scholar]


























| Item | Nodes in Axial Direction | Nodes in Radial Direction | Number |
|---|---|---|---|
| Mesh Program 1 | 600 | 60 | 35,345 |
| Mesh Program 2 | 1000 | 90 | 88,915 |
| Mesh Program 3 | 1500 | 120 | 178,385 |
| Mesh Program 4 | 2000 | 150 | 297,855 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, C.; Wang, X.; Mao, S.; Kang, Y.; Lu, Y.; Han, X.; Liu, W. Heat Transfer Characteristics and Prediction Model of Supercritical Carbon Dioxide (SC-CO2) in a Vertical Tube. Energies 2017, 10, 1870. https://doi.org/10.3390/en10111870
Cai C, Wang X, Mao S, Kang Y, Lu Y, Han X, Liu W. Heat Transfer Characteristics and Prediction Model of Supercritical Carbon Dioxide (SC-CO2) in a Vertical Tube. Energies. 2017; 10(11):1870. https://doi.org/10.3390/en10111870
Chicago/Turabian StyleCai, Can, Xiaochuan Wang, Shaohua Mao, Yong Kang, Yiyuan Lu, Xiangdong Han, and Wenchuan Liu. 2017. "Heat Transfer Characteristics and Prediction Model of Supercritical Carbon Dioxide (SC-CO2) in a Vertical Tube" Energies 10, no. 11: 1870. https://doi.org/10.3390/en10111870
APA StyleCai, C., Wang, X., Mao, S., Kang, Y., Lu, Y., Han, X., & Liu, W. (2017). Heat Transfer Characteristics and Prediction Model of Supercritical Carbon Dioxide (SC-CO2) in a Vertical Tube. Energies, 10(11), 1870. https://doi.org/10.3390/en10111870