A Novel Two-Stage Photovoltaic Grid-Connected Inverter Voltage-Type Control Method with Failure Zone Characteristics
Abstract
:1. Introduction
2. Power Transmission Characteristics of Grid-Connected Inverter
3. Failure Zone of Synchronous Generator Governor
3.1. The Cause of Failure Zone
3.2. Static Frequency Characteristics Considering the Failure Zone
3.3. The Effect of Failure Zone on Frequency Regulation
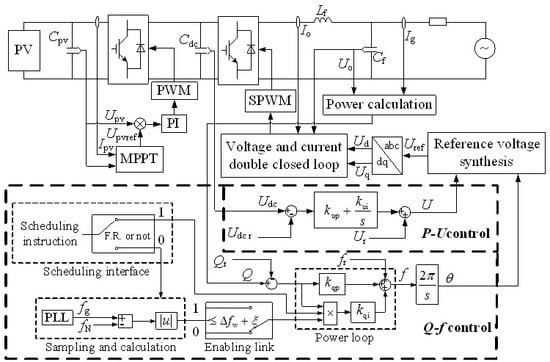
4. Novel Two-Stage Voltage-Type Grid-Connected Photovoltaic Inverter Control Method with Failure Zone Characteristics
4.1. Design Logic of Failure Zone
4.2. Novel Two-Stage Photovoltaic Grid-Connected Inverter Voltage-Type Control Method
4.2.1. Active Power-Voltage Control
4.2.2. Reactive Power-Frequency Control
4.2.3. Overall Control Scheme of the Inverter
5. Verification
5.1. The Dynamic Characteristics of the Source
5.2. Verification of Direct Current (DC) Voltage Loop
5.3. Verification of Failure Zone Characteristics
5.4. Verification of the Dispatching Interface
6. Conclusions
- (1)
- In this paper, based on the characteristics of speed governor system of the conventional generator, the traditional static frequency characteristics are corrected. Then a novel two-stage grid-connected photovoltaic inverter voltage-type control method with the characteristics of the governor’s failure zone is proposed. The dynamic balance between resisting fluctuations, participation in frequency regulation and dispatching response is achieved.
- (2)
- Through the improvement of the droop control and the design of the power enabling link, the inverter possesses the failure zone characteristics of the synchronous generator. For small frequency fluctuations inside the failure zone, the inverter maintains a constant output. If the frequency fluctuation exceeds the failure zone, the inverter participates in grid frequency regulation according to the droop relationship.
- (3)
- Whether or not the inverter participates in frequency regulation should be controllable rather than completely autonomous, especially when there are many renewable energy sources. The design of the dispatch interface ensures the schedulability of the inverter.
- (4)
- The frequency regulation delay of renewable energy was introduced to improve inverters’ adaptability to renewable energy penetration rate. Therefore, the proposed control scheme can achieve the best operating state in an environment with any renewable energy penetration rate through flexible parameter settings.
- (5)
- A DC voltage loop was designed, which has two roles. On the one hand, it stabilizes the DC bus voltage to achieve operations without energy storage. On the other hand, it ensures that the system is not affected by the grid and delivers the maximum power to the grid stably.
- (6)
- The selection of failure zone thresholds for renewable energy based inverters and coordinated control of multi-inverters can be researched in the future.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Meaning and Symbols | Value |
|---|---|
| Maximum power of photovoltaic array Ppvmax | 12.5 kW |
| The capacitor on the output side of the photovoltaic array Cpv | |
| Capacitor at DC (direct current) bus Cdc | |
| Filter inductor Lf | 2.2 mH |
| Filter capacitor Cf | |
| The amplitude of the inverter’s rated output voltage Ur | V |
| The reference value of inverter’s DC voltage Udcr | 800 V |
| Inverter rated frequency fr | 50 Hz |
| Inverter rated output reactive power Qr | 0 var |
| The proportional gain of the reactive power loop kqp | 0.0001 |
| The integral gain of the reactive power loop kqi | 0.0015 |
| The proportional gain of the DC voltage loop kup | 0.5 |
| The integral gain of the DC voltage loop kui | 3 |
| The proportional gain of the voltage loop koup | 1.4 |
| The integral gain of the voltage loop koui | 3.2 |
| The proportional gain of the current loop koip | 1 |
| The integral gain of the current loop koii | 0 |
| 0.033 Hz | |
| 50.033 Hz | |
| 49.967 Hz | |
| The frequency regulation delay of the inverter | 0.067 Hz |
| 0.1 Hz |
Appendix B

References
- Bose, B.K. Global energy scenario and impact of power electronics in 21st century. IEEE Trans. Ind. Electron. 2013, 60, 2638–2651. [Google Scholar] [CrossRef]
- Zhou, Y.; Gong, D.C.; Huang, B.; Peters, B.A. The impacts of carbon tariff on green supply chain design. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1542–1555. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, X.; Pedram, M. A near-optimal model-based control algorithm for households equipped with residential photovoltaic power generation and energy storage systems. IEEE Trans. Sustain. Energy 2016, 7, 77–86. [Google Scholar] [CrossRef]
- Cho, Y.W.; Cha, W.J.; Kwon, J.M.; Kwon, B.H. Improved single phase transformerless inverter with high power density and high efficiency for grid-connected photovoltaic systems. IET Renew. Power Gener. 2016, 10, 166–174. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of power converters in ac microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Strasser, T.; Andrén, F.; Kathan, J.; Kathan, J.; Kathan, J.; Siano, P.; Siano, P.; Zhabelova, G.; Zhabelova, G.; Vrba, P.; Mařík, V. A review of architectures and concepts for intelligence in future electric energy systems. IEEE Trans. Ind. Electron. 2015, 62, 2424–2438. [Google Scholar] [CrossRef]
- Daher, S.; Schmid, J.; Antunes, F.L.M. Multilevel inverter topologies for stand-alone PV systems. IEEE Trans. Ind. Electron. 2008, 55, 2703–2712. [Google Scholar] [CrossRef]
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. A review of single phase grid connected inverters for photovoltaic modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- Kim, K.A.; Seo, G.S.; Cho, B.H.; Krein, P.T. Photovoltaic hot-spot detection for solar panel substrings using AC parameter characterization. IEEE Trans. Power Electron. 2016, 31, 1121–1130. [Google Scholar] [CrossRef]
- Debnath, D.; Chatterjee, K. Two-stage solar photovoltaic-based standalone scheme having battery as energy storage element for rural deployment. IEEE Trans. Ind. Electron. 2015, 62, 4148–4157. [Google Scholar] [CrossRef]
- Alajmi, B.N.; Ahmed, K.H.; Finney, S.J.; Williams, B.W. A maximum power point tracking technique for partially shaded photovoltaic systems in microgrids. IEEE Trans. Ind. Electron. 2013, 62, 1596–1606. [Google Scholar] [CrossRef]
- Choi, W.Y. Three-level single-ended primary-inductor converter for photovoltaic power conditioning systems. Sol. Energy 2016, 62, 43–50. [Google Scholar] [CrossRef]
- Kanaan, H.; Caron, M.; Al-Haddad, K. Design and implementation of a two-stage grid-connected high efficiency power load emulator. IEEE Trans. Power Electron. 2014, 29, 3997–4006. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, S.; Shen, A. Carrier-overlapping PWM-based hybrid current control strategy applied to two-stage grid-connected PV inverter. IET Power Electron. 2018, 11, 182–191. [Google Scholar] [CrossRef]
- Boukezata, B.; Gaubert, J.P.; Chaoui, A.; Hachemi, M. Predictive current control in multifunctional grid connected inverter interfaced by PV system. Sol. Energy 2016, 391, 130–141. [Google Scholar] [CrossRef]
- Vasquez, V.; Ortega, L.M.; Romero, D.; Ortega, R.; Carranza, O.; Rodriguez, J.J. Comparison of methods for controllers design of single phase inverter operating in island mode in a microgrid: Review. Renew. Sustain. Energy Rev. 2017, 76, 256–267. [Google Scholar] [CrossRef]
- Singh, M.; Khadkikar, V.; Chandra, A.; Varma, R.K. Grid interconnection of renewable energy sources at the distribution level with power quality improvement features. IEEE Trans. Power Deliv. 2011, 26, 307–315. [Google Scholar] [CrossRef]
- De Paiva, E.P.; Vieira, J.B.; De Freitas, L.C.; Farias, V.J.; Coelho, E.A.A. Small signal analysis applied to a single phase inverter connected to stiff AC system using a novel improved power controller. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 6–10 March 2005. [Google Scholar]
- Avelar, H.J.; Parreira, W.A.; Vieira, J.B.; De Freitas, L.C.G.; Coelho, E.A.A. A State Equation Model of a Single-Phase Grid-Connected Inverter Using a Droop Control Scheme with Extra Phase Shift Control Action. IEEE Trans. Power Deliv. 2012, 59, 1527–1537. [Google Scholar] [CrossRef]
- Verma, V.; Khushalani-Solanki, S.; Solanki, J. Modeling and Criterion for Voltage Stability of Grid Connected Droop Controlled Inverter. In Proceedings of the 2017 North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017. [Google Scholar]
- Zhong, Q.C. Power electronics-enabled autonomous power systems: Architecture and technical routes. IEEE Trans. Ind. Electron. 2017, 64, 5907–5918. [Google Scholar] [CrossRef]
- Yan, X.W.; Zhang, X.Y.; Zhang, B.; Ma, Y.J.; Wu, M. Research on Distributed PV Storage Virtual Synchronous Generator System and Its Static Frequency Characteristic Analysis. Appl. Sci. 2018, 8, 532. [Google Scholar] [CrossRef]
- Vinayagam, A.; Alqumsan, A.A.; Swarna, K.S.V.; Khoo, S.Y.; Stojcevski, A. Intelligent control strategy in the islanded network of a solar PV microgrid. Electr. Power Syst. Res. 2018, 155, 93–103. [Google Scholar] [CrossRef]
- Grainger, J.J.; Stevenson, W.D.J. Power System Analysis; Stephen, E.H., Ed.; McGraw-Hill: Hightstown, NJ, USA, 1994; pp. 562–572. [Google Scholar]
- Viinamäki, J.; Kuperman, A.; Suntio, T. Grid-Forming-Mode Operation of Boost-Power-Stage Converter in PV-Generator-Interfacing Applications. Energies 2017, 10, 1033. [Google Scholar] [CrossRef]
- Moradi, M.H.; Reisi, A.R. A hybrid maximum power point tracking method for photovoltaic systems. Sol. Energy 2011, 85, 2965–2976. [Google Scholar] [CrossRef]












© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Zhang, X.; Zhang, B.; Jia, Z.; Li, T.; Wu, M.; Jiang, J. A Novel Two-Stage Photovoltaic Grid-Connected Inverter Voltage-Type Control Method with Failure Zone Characteristics. Energies 2018, 11, 1865. https://doi.org/10.3390/en11071865
Yan X, Zhang X, Zhang B, Jia Z, Li T, Wu M, Jiang J. A Novel Two-Stage Photovoltaic Grid-Connected Inverter Voltage-Type Control Method with Failure Zone Characteristics. Energies. 2018; 11(7):1865. https://doi.org/10.3390/en11071865
Chicago/Turabian StyleYan, Xiangwu, Xueyuan Zhang, Bo Zhang, Zhonghao Jia, Tie Li, Ming Wu, and Jun Jiang. 2018. "A Novel Two-Stage Photovoltaic Grid-Connected Inverter Voltage-Type Control Method with Failure Zone Characteristics" Energies 11, no. 7: 1865. https://doi.org/10.3390/en11071865
APA StyleYan, X., Zhang, X., Zhang, B., Jia, Z., Li, T., Wu, M., & Jiang, J. (2018). A Novel Two-Stage Photovoltaic Grid-Connected Inverter Voltage-Type Control Method with Failure Zone Characteristics. Energies, 11(7), 1865. https://doi.org/10.3390/en11071865