Correlation Analysis between Wind Speed/Voltage Clusters and Oscillation Modes of Doubly-Fed Induction Generators

Abstract

Potential machine-grid interactions caused by large-scale wind farms have drawn much attention in recent years. Previous work has been done by analyzing the small–signal modeling of doubly-fed induction generators (DFIGs) to obtain the oscillation modes. This paper, by making use of the metered power data of wind generating sets, studies the correlation between oscillation modes of the DFIG system and influence factors which includes wind speed and grid voltage. After the metered data is segmented, the Prony algorithm is used to analyze the oscillation modes contained in the active power. Then, the relevant oscillation modes are extracted in accordance with the small-signal analysis results. Meanwhile, data segments are clustered according to wind speed and grid voltage. The Apriori algorithm is finally used to discuss the association rules. By training the mass of data of wind generating sets, the inevitable association rules between oscillation modes and influence factors can be mined. Therefore, the prediction of oscillation modes can be achieved based on the rules. The results show that the clustering number quite affects the association rules. When the optimal cluster number is adopted, part of the wind speed/voltage clusters can analyze the certain oscillation modes. The predicted results are quite consistent with the practical data.

1. Introduction

According to the 2016 Global Wind Power Development Outlook Report, the wind power market will reach 100 GW by 2020, and the cumulative wind power market will reach 879 GW [1]. With the continuous increase of wind power penetration, the machine-grid interaction has attracted increasing attention. It is found that the interaction is usually reflected in the oscillation of active power [2]. The oscillation modes can be divided into sub-synchronous interaction and low frequency oscillation. The former can be categorized into sub-synchronous control interaction (SSCI) and sub-synchronous torque interaction (SSTI). SSTI includes sub-synchronous oscillation (SSO) [3] and sub-synchronous resonance (SSR) [4]. Since the 1960s, accidents caused by machine-grid interactions have occurred in Europe, America and other countries. The first SSCI accident caused by an interaction between the rotor-side converter and the fixed string compensation system of the doubly-fed induction generator (DFIG) happened in Texas (USA). It resulted in damage to the wind turbines and internal lever circuits [5].

At present, research on the machine-grid interaction is mainly based on modeling and simulation. For instance, Reference [6] proposes a unified modularized small signal dynamic model of wind farm based on an induction motor. It can simulate a random number of fixed speeds, some variable speed (doubly-fed) induction motor wind turbine, providing a lot of flexibility for wind turbines and their controllers. In [7], a small-signal model of the direct-drive permanent magnet synchronous generator is established to study the stability of the grid-connected wind generating sets after the small disturbance, and the parameters of the controller are designed effectively. Reference [8] aimed at the suppression of torsional vibrations caused by small electrical disturbances from the grid side in a DFIG-based wind turbine system. The Prony algorithm is a complementary method used in the time-domain model system. It decomposes time-domain signals into damped sinusoids with four parameters per mode: frequency, damping, amplitude and phase. Compared with small-signal analysis, the Prony analysis shows an advantage when the system turns complicated because the former has difficulty solving high-order matrix [9,10]. All the papers above investigated the wind power oscillation mechanism and suppression method by modeling methods. However, the operation of wind generating sets is affected by factors which are more complex than the modeling simulation. A more direct and convenient way is to directly use the metered data.

With the advent of the big data era, the vast amounts of data collected from wind farms conceals vast information [11]. Data mining and machine learning theory including correlation analysis, cluster analysis, classification analysis, have brought new ideas to power research [12]. Among them, the Apriori algorithm, one of the correlation algorithms, provides an effective solution for exploring the association relationship between large data item-sets. In the power industry, correlation analysis is mainly used for transformer fault diagnosis. The Apriori algorithm is a common tool of correlation analysis. The Apriori algorithm is a hierarchical algorithm, which seeks frequent item-sets in the increasing item number order. The algorithm can be divided into two steps. The first step is to generate frequent item-sets with minimum support condition. The second step is to produce association rules with minimum confidence condition [13,14]. In [15], a data-driven method of association rule mining for transformer state parameters is proposed by combining the Apriori algorithm and probabilistic graphical model. Paper [16] proposes a new fault diagnosis method based on Set Pair Analysis and association rules. Via analyzing the relationship of fault symptoms and fault types, the corresponding association rules are established. In addition, cluster analysis, as an unsupervised classification method, provides a solution for the information mining of large quantity unknown data [17]. Reference [18] clusters the photovoltaic power station according to the geographical space and analyzes the evolution characteristics of cluster center and cluster radius to predict the spatio-temporal expansion of photovoltaic power supply. Based on new wind pattern recognition technologies, Reference [19] proposes a short-term wind power predicting method for a wind power farm. The correlation between wind power data and numerical weather prediction is used to cluster the meteorological grid data first, and then to construct artificial neural network and support vector machine model for each cluster to improve the accuracy of prediction. However, limited research has been done into the oscillation of wind generating sets through big data technology.

In this paper, metered actual output power data of wind generating sets will be used to mine the association rules between oscillation modes and influence factors. Based on the mode analyzing results via the small-signal modeling of DFIG, the information of the machine-grid interaction embedded in the actual operation data will be mined. The Prony algorithm will be used as the fundamental signal analysis method to do the preliminary signal decomposition. As a big data analysis technology, the Apriori algorithm will be introduced to make further efforts on the association rules mining and oscillation prediction. The association rules between clusters and oscillation modes through the analysis of metered data will be obtained. The prediction reveals the comprehensive impact of wind speed and voltage factors on the oscillation modes that may be contained in wind power.

The novelty of this paper is that it: (i) combines the modeling method and data analysis method to mine the oscillation information in the practical data of wind power; (ii) establishes the association analyzing modeling based on the Apriori algorithm to analyze the association rules between wind speed/voltage fluctuation clusters and oscillation modes; (iii) proposes a prediction method for the wind power oscillation modes.

The rest of the paper is organized as follows: Section 2 introduces the research methods of the oscillation modes of wind generating sets from two aspects: modeling and data analysis. Section 3 establishes the data correlation analysis model of the wind generating sets. The data is segmented by the wind speed and the segments are clustered according to the wind speed and the voltage fluctuation. Section 4 is a case analysis, where the impact of cluster number set on association rules is analyzed, and the predict is done according to the association rules between wind power and wind speed/voltage clusters, and the conclusion is given finally.

2. Study of Oscillation Modes of Grid-Connected DFIG System

Based on the structure of a grid-connected DFIG system, the small-signal system of DFIG has been established and used to analyze the oscillation modes to obtain the results of the modeling analysis. Meanwhile, the Prony algorithm is introduced to analyze the metered power data and the result is compared with the characteristic frequencies obtained from the modeling analysis.

2.1. Oscillation Modes Analysis Based on the Small-Signal Model

The detailed structure of the grid-connected DFIG system is shown in Figure 1.

Three-mass block model, which is more suitable for dynamic analysis, is applied here. The mechanical rotation system of the DFIG can be divided into three parts namely blade, low-speed shaft and high-speed shaft. The low-speed shaft connects the blades to the gearbox, and the high-speed shaft connects the gearbox to the induction generator unit. In addition, the output of the rotor circuit enters the power grid via the converter device, while the stator circuit is directly connected to the external power grid [8,20].

The main objective of the machine-side converter control is to stabilize the active power and machine voltage of DFIG. Vector control is adopted based on stator flux orientation, and the coordinate system of which d-axis and stator flux are coincident is introduced. The active power and voltage are controlled by u_qr and u_dr, respectively. The control goal of the network-side converter is to stabilize the DC side voltage and reactive power. The current component i_dg and i_qg are used to realize the control respectively by the grid-side converter. The rotating coordinate system is consistent with the generator. The symbols of electric parameters do not make a distinction in the coordinate system. The control block diagrams of the machine-side converter and network-side converter are shown in Figure 1. Based on the system structure above, the small-signal model of grid-connected DFIG is shown in Figure 2.

By using the small-signal model, the distribution of the system eigenvalue can be analyzed. The characteristic values corresponding to non-oscillatory form and high-frequency resonance are eliminated to focus on the machine-grid interaction. The characteristic frequency to be reserved is between 0 and 100 Hz. The result is shown in

Table 1. Eigenvalues of DFIG connected to grid.

Type	Eigenvalues	Mode Frequency (Hz)	Damping Ratio
SSR	−23.63 ± 498i	79.25	0.0474
	−16.75 ± 147i	23.40	0.1132
SSO	−1.477 ± 77.97i	12.41	0.0189
	−11.72 ± 12.08i	1.92	0.6963
SSCI	−51.17 ± 285.1i	45.37	0.1767
	−8.91 ± 27.45i	4.37	0.3087
Low frequency oscillation	−0.319 ± 3.177i	0.51	0.1

[20].

In the analysis below, these mode frequencies will be used as reference values for frequency screening to classify metered data.

2.2. Study of Oscillation Modes Based on Metered Data

2.2.1. Prony Algorithm

For time series generated by interval sampling, Prony algorithm is commonly used for curve fitting with the linear combination of exponent items [10]. Its discretization expression is:

$$\widehat{x}\left(n\right)={\displaystyle \sum _{i=1}^p{b}_i{z}_i^n}={\displaystyle \sum _{i=1}^p{A}_i\exp ({\alpha }_{i}n)\sin (2\pi f_{i}n+{\phi }_i)}$$

(1)

in which:

$$\{\begin{array}{l}{b}_i=A_i\exp (j{\phi }_i)\\ z_i=\exp [({\alpha }_i+j2\pi f_i)\Delta t]\end{array}$$

(2)

where, A_i, α_i, f_i, ϕ_i (i = 1, 2, …, n) respectively represent the amplitude, attenuation factor, frequency and initial phase Angle of the ith fitting component; p is the component number of fitting functions; n = 1, 2, ..., N − 1, N is the number of fitting points.

The Prony algorithm is a fitting algorithm, and the objective function is the error function shown in (3):

$$\min \left[\epsilon ={\displaystyle \sum _{n=0}^{N-1}{\left|x\left(n\right)-\widehat{x}\left(n\right)\right|}^2}\right]$$

(3)

Using the least squares method, the value of the unknown parameter in Equation (1) can be obtained. The original sequence can be decomposed into attenuation components and DC components.

2.2.2. The Oscillation Modes Analysis under Fixed Wind Speed Using the Prony Algorithm

Based on the metered data of the wind generating sets, the output power curve is plotted in Figure 3.

The analysis results of the Prony algorithm are shown in

Table 2. Results of the Prony analysis.

Amplitude	Frequency (Hz)	Damping Ratio (%)
190,696	0.143 (low-frequency oscillation)	−37.127
75,562	19.466	3.712
63,194	40.545	4.535
62,034	50.307	6.586
36,437	0	100
34,919	35.2	2.06
28,455	6.748	6.501
26,792	20.582	1.218
24,909	10.449	11.286
24,175	40.556	1.65
22,959	15.242	2.607
16,312	8.433	5.332
14,049	26.189	2.883
13,875	17.107	−0.473
12,269	32.948	0.082
11,490	63.518	0.154
10,384	68.174	1.121
9987	3.107	−2.071
9528	23.523 (SSR)	0.008
9465	12.404 (SSO)	0.865

. The oscillation frequencies higher than 100 Hz are eliminated for exceeding the frequency range between 0 and 100 Hz of machine-grid interactions.

It can be concluded from the above data that the low frequency oscillation, SSCI, SSO, and SSR exist in the process of actual system operation. However, the frequencies obtained by the metered data slightly deviate from the characteristic frequency calculated by the small-signal model. Therefore, frequency filtrating rules are designed in

Table 3. Frequency filtrating rules.

Machine-Grid Interaction Type	Oscillation Modes from Small Signal Model (Hz)	Filtrate Range of Prony Analysis Result (Hz)	Correlation Analysis Mark Tag
Low-frequency oscillation	0.1–1.8 Hz	[0.1, 1.8]	1
		other	0
SSCI	4.37 Hz	[4.17, 4.57]	1
		other	0
	45.37 Hz	[44.57, 46.17]	1
		other	0
SSO	12.41 Hz	[11.91, 12.91]	1
		other	0
	1.92 Hz	[1.82, 2.02]	1
		other	0
SSR	79 Hz	[77.5, 80.5]	1
		other	0
	23 Hz	[22.4, 23.6]	1
		other	0

.

When the oscillation frequency in the Prony analysis result appears in a certain screening range in Table 3, it can be considered that the analyzed object contains the corresponding oscillation mode component.

3. Modeling of the Correlation Analysis of Wind Speed/Voltage Factors and Oscillation Modes

3.1. K-Means Clustering

According to the project observation, the machine-grid interaction of the wind turbine often occurs at low wind speeds. Meanwhile, the voltage change at the PCC point also has the same effect. Thus, the K-Means algorithm is used to find out the influence of both two factors on the oscillation mode by clustering the metered data according to wind speed and voltage. As a result, influence factors in the same cluster have the same characteristics.

The K-Means algorithm is an iterative clustering algorithm. The given data set is divided into the specified k clusters [11]. In the data transformation process, influencing factors include wind speed and three-phase voltage fluctuation. To explore the effects of these whole factors on the oscillation modes, clustering can be done first for the same cluster has the same characteristics and influence on the oscillation modes. When the factors number to be considered is d, the input object is the d-dimensional point set and the output is to assign each point to one cluster. The entire analysis object can be represented by the set C, and one element in C can be expressed as (4):

$$C\left(i\right)=c\left(x_{i1},x_{i2},\cdots ,x_{id}\right)$$

(4)

in which, x_ij (j = 1, 2, …, d) represents wind speed, three-phase voltage fluctuation and so on. The Euclidean distance between two d-dimensional vectors is shown in (5):

$$d_{12}=\sqrt{{\displaystyle \sum _{k=1}^d{(x_{1k}-x_{2k})}^2}}$$

(5)

The K-Means algorithm minimizes the total Euclidean distance between each point and the cluster center. In this paper, the optimal cluster number is first selected with fewer sampling data. It is necessary to record the cluster center of the optimal cluster number to be set as the initial cluster center in the later analysis, which ensures the consistency of clustering results.

3.2. Association Rules and the Improved Apriori Algorithm

Assume that set D represents the wind power data set, which is the input data of the correlation analysis. If there is association rule “Cluster1$\to$SSTI”, it means that when the influencing factors are clustered in cluster 1, it is very likely that the output power oscillation mode contains “SSTI”. “Cluster1” and “SSTI” are both wind power data item set. The item set is also likely to be the clustering combination like “Cluster1& Cluster2” or oscillation modes like “SSR”.

According to [14,15], for the association rule “Cluster1$\to$SSTI”, the support degree “support(Cluster1$\to$SSTI)” is the percentage of transactions that “Cluster1” and “SSTI” occurs at the same time to the total transactions, shown in (6):

$$\mathrm{support}(\mathrm{Cluster}1\to \mathrm{SSTI})=\frac{\mathrm{count}(\mathrm{Cluster}1\cap \mathrm{SSTI})}{\mathrm{count}(\mathrm{D})}$$

(6)

Confidence coefficient confidence(Cluster1$\to$SSTI) is the proportion of appearance of “SSTI” given that “Cluster1” happens, shown in (7):

$$\mathrm{confidence}(\mathrm{Cluster}1\to \mathrm{SSTI})=\frac{\mathrm{support}(\mathrm{Cluster}1\cap \mathrm{SSTI})}{\mathrm{support}(\mathrm{Cluster}1)}$$

(7)

In transaction set D, the rule satisfying the minimum support condition minsup and the minimum confidence condition minconf is the strong association rule.

In this paper, the time cost of scanning can be reduced because the preceding item is limited in the cluster item-set and the subsequent item is limited in oscillating mode item-set. The first step is to use the hierarchical sequential search method which is the same as the Apriori algorithm.

The difference is that the frequent 1 item-set is searched in the oscillating modes, while from frequent 2 item-set, the search area is reduced to the cluster item-set. The frequent k item-set are then used to generate frequent (k + 1) item-set. The circulation is done until the new frequent sets cannot be found. When producing frequent k item-set, Apriori mainly accomplishes two tasks, connecting and cutting. The connection process happens when a candidate item-set is generated by connecting the frequent k − 1 item-sets. The cutting process is to get rid of nonfrequent item-set according to the minimum support threshold. Thus, the frequent k item-set is obtained.

Due to the limitation in the first step, the frequent item set contains only one oscillation mode as consequent denoted by q. After all the frequent item-sets are found, the second step is to generate association rules by corresponding the different subset p_ji (i = 1, 2, ..., n) of frequent preceding item-set p_j (j = 1, 2, ... m) with q exclusive to different subsequent item-set q_j, and then calculating the confidence level by (8):

$$\frac{\mathrm{support}(q_j)}{\mathrm{support}(p_{ji})}\ge \min conf$$

(8)

when the inequality is satisfied, the rule “$p_{ji}\to q_i$”can be output. The improved algorithm flow is shown in Figure 4. To show the advantages of the Improved algorithm more clearly, comparison tabulation between ‘Improved Apriori Algorithm’ and ‘Apriori algorithm’ is given by

Table 4. Comparison between ‘Improved Apriori Algorithm’ and ‘Apriori algorithm’.

Comparison Item	Search Method	Item Restriction	Time Cost
Apriori Algorithm	Traverse the data set	The preceding item and subsequent item are unrestricted	High
Improved Apriori Algorithm	Search in the appointed data set	The preceding item and subsequent item are restricted	Low

.

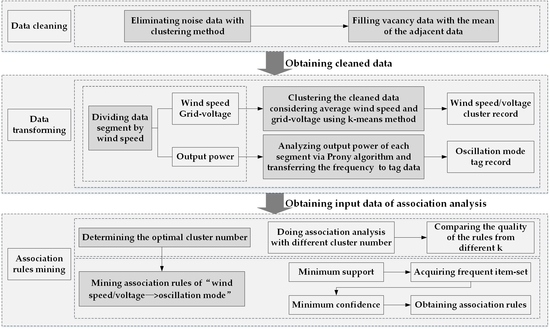
3.3. Modeling of the Correlation Analysis

Based on the algorithm above, the correlation analysis model of wind speed/voltage fluctuation clusters and oscillation modes is established. The modeling process is shown in Figure 5.

In this paper, the data wind generating sets of is based on the sampling frequency of 4000 Hz, including wind speed, grid-connected voltage and current information.

Firstly, the raw data is cleaned, and then the original data is clustered by K-Means cluster algorithm to find out and eliminate the noise data. Then, the mean of the data before and after the vacant is used to fill the empty data.

To study the influence of wind speed and voltage on the oscillation modes of wind generating sets, the preprocessed data was firstly divided into segments according to the wind speed, and the sectional flow chart is shown in Figure 6.

Original data is read and written into a data segment according to wind speed value in sampling sequence. When wind speed change rate is more than 0.05 m/s, a new data segment is built and used to record the subsequent data. This circulation is done until the final data segment is obtained. The sampling point of each data segment is approximately 4000. The sampling data in the same data segment is analyzed. Records can be extracted from each data segment time sequence, and act as the input of correlation analysis. After the data is segmented according to wind speed, the mean of wind speed in each segment is recorded in the corresponding record.

The voltage effective value is calculated according to the sliding window principle. The influence of voltage fluctuation on the power oscillation modes is required to be observed, so in each data segment, the difference between the maximum and the minimum of the three phase rms voltage is used as the indicator of the voltage fluctuations is shown in (9). Total voltage fluctuation takes the average of three phase fluctuations as is shown in (10):

$$\{\begin{array}{l}\Delta V_{\mathrm{A}}=V_{\mathrm{A}rms\max }-V_{\mathrm{A}rms\min }\\ \Delta V_{\mathrm{B}}=V_{\mathrm{B}rms\max }-V_{\mathrm{B}rms\min }\\ \Delta V_{\mathrm{C}}=V_{\mathrm{C}rms\max }-V_{\mathrm{C}rms\min }\end{array}$$

(9)

$$\Delta V=\left(\Delta V_{\mathrm{A}}+\Delta V_{\mathrm{B}}+\Delta V_{\mathrm{C}}\right)/3$$

(10)

Thus, each data segment record stores a wind speed value, three phase voltage fluctuation indicators, and a total voltage fluctuation value. In order to study the combined effects of these factors, the data segments studied were clustered according to wind speed, $\Delta V_{\mathrm{A}}$, $\Delta V_{\mathrm{B}}$, $\Delta V_{\mathrm{C}}$, and $\Delta V$. The clustering results are recorded in are the corresponding data segment. When k = 6, if a data segment is clustered in cluster 1, the cluster tag of this data segment is [cluster 1, cluster 2, cluster 3, cluster 4, cluster 5, cluster 6] = [1, 0, 0, 0, 0, 0].

Meanwhile, Prony analysis is performed on each data segment. The mode analysis results of the small-signal model in the second part are used to filtrate oscillation frequency within a certain error range and the filtering rules are shown in Table 3.

The oscillation mode tag data and the cluster tag data are summarized to be the input data of correlation analysis. Then the association rules can be analyzed. Finally, the association rules can be obtained.

4. Correlation Analysis between Wind Speed/Voltage Cluster and Oscillation Modes of Wind Generating Sets

In this part, 807 data segments are chosen to be the sampling segments to select an optimal clustering number. Association results using different k values are compared first and the optimal one is chosen for further analysis.

4.1. Influence of Cluster Number k on Correlation Analysis Result

807 data segments are used as a sample to seek the optimal k value. The data segments are clustered by different k values namely k = 6, k = 8, and k = 10. The clustering results are shown in Figure 7 below.

When k = 6, it can be seen from Figure 7a that the 807 5-dimensional data points are divided into six clusters. Cluster 1 is the black data point set in the graph, which has the characteristics of 3~5 m/s wind speed and 1.7~2.5 V total voltage fluctuation. Cluster 2 is the red data point set in the figure, which has the characteristics of more than 3.5 m/s wind speed and 0~0.8 V voltage fluctuation. Cluster 3 is the green data point set in the graph. This cluster has the characteristics of wind speed greater than 5 m/s and the voltage fluctuation greater than 2 V. Cluster 4 is the dark blue data point set in the picture, and it is also the most abundant cluster and is the state that occurs most often. The wind speed of cluster 4 is 3.5~4.5 m/s, and the voltage fluctuation is normal 1~1.7 V. Cluster 5 is the light blue data point set in the figure. The wind speed of the cluster is less than 3.5 m/s and the voltage fluctuation is between 1~1.7 V. Cluster 6 is the red data point set in the graph. The cluster has the characteristics of voltage fluctuation greater than 2.2 V and wind speed of 4~5.5 m/s. Therefore, after clustering, data points with the same characteristics of wind speed and voltage fluctuation are clustered into the same cluster.

When k = 8, as shown in Figure 7b, clusters 1, 3, and 6 in Figure 7a are subdivided into 4 clusters. The cluster 4 and 5 in Figure 7a are subdivided into three clusters. And when k = 10, as is shown in Figure 7c, the cluster 2 in Figure 7b is further subdivided into two clusters, clusters 2 and cluster 3 respectively. There are only three points in cluster 3, and the voltage fluctuation is less than 0.4 V, which can be considered as the abnormal data point. These points are filtered out and ignored in subsequent correlation analysis under minimal support condition. In addition, the cluster 9 in Figure 7b is further subdivided into clusters 8 and 9 in Figure 7c, and the range of cluster 8 and 9 is intersected. The wind speed, three-phase voltage fluctuation and total voltage fluctuation are considered in the clustering, but the subdivision is not necessary in terms of the total voltage fluctuation and wind speed. Therefore, nine clusters scene is likely to be the best case from the clustering result. The data is clustered again with k = 9 and the clustering results are shown in Figure 8.

To further determine the optimal cluster number, a new comparison is made by comparing the correlation analysis results of different k values namely k = 8, k = 9 and k = 10.

4.1.1. The Same Data Segment Correspondence

To study the effect of wind speed and voltage fluctuation on the oscillation frequency in the same data segment, the cluster tag data is set as input and the oscillation mode tag in the same data segment is the target. Different clustering numbers namely k = 8, k = 9 and k = 10 achieve different association rules as is shown in

Table 5. Association rules (the same data segment correspondence).

k	No.	Preceding Item	Subsequent Item	Support (%)	Confidence (%)
8	1	0.1–1.8 Hz	cluster 3	6.1958	42.0000
	2	23 Hz	cluster 4	18.0917	41.0959
	3	45.37 Hz	cluster 7	9.7893	39.2405
	4	12.41 Hz	cluster 3	6.1958	38.0000
	5	45.37 Hz	cluster 1	4.9566	37.5000
	6	23 Hz	cluster 8	42.2553	36.9501
	7	45.37 Hz	cluster 8	42.2553	36.6569
	8	23 Hz	cluster 3	6.1958	36.0000
	9	0.1–1.8 Hz	cluster 4	18.0917	34.9315
	10	23 Hz	cluster 7	9.7893	34.1772
	11	0.1–1.8 Hz	cluster 5	4.2131	32.3529
	12	45.37 Hz	cluster 5	4.2131	32.3529
9	1	0.1–1.8 Hz	cluster 6	6.0719	42.8571
	2	23 Hz	cluster 5	20.4461	41.8182
	3	45.37 Hz	cluster 7	9.4176	40.7895
	4	12.41 Hz	cluster 6	6.0719	38.7755
	5	45.37 Hz	cluster 2	4.9566	37.5000
	6	23 Hz	cluster 7	9.4176	36.8421
	7	45.37 Hz	cluster 3	37.6704	35.8553
	8	23 Hz	cluster 3	37.6704	35.8553
	9	23 Hz	cluster 6	6.0719	34.6939
	10	0.1–1.8 Hz	cluster 5	20.4461	34.5455
	11	45.37 Hz	cluster 4	6.9393	33.9286
	12	23 Hz	cluster 4	6.9393	30.3571
10	1	45.37 Hz	cluster 5	8.4263	42.6471
	2	23 Hz	cluster 1	20.4461	41.8182
	3	45.37 Hz	cluster 4	4.9566	37.5000
	4	23 Hz	cluster 5	8.4263	36.7647
	5	0.1–1.8 Hz	cluster 1	20.4461	34.5455

.

The threshold is adjusted so that the associated rules of output will have higher confidence and support. The support value should not be set too large, or it will result in missing some strong association rules. Therefore, a small support threshold is set at first, and the output rules are sorted by confidence level. The rules with high confidence level are selected and the lowest support value among them is chosen as the support threshold. And the confidence threshold can be set as the minimum confidence value among the selected rules. After the adjusting, the minsup is set as 4, and minconf is 30. For comparison convenience, the main parameters of the rules with different k are presented in

Table 6. Statistics comparison of association rules with different k values (the same data segment correspondence).

Comparison Item	k = 8	k = 9	k = 10
Rule number	12	12	5
Minimum support	4.213%	4.957%	4.957%
Maximum support	42.255%	37.67%	20.446%
Average support (%)	14.3536	14.3432	12.5403
the standard deviation of support	13.8834	12.1143	7.3547
Mid-value of support	7.9926	8.1784	8.4263
Minimum confidence	32.353%	30.357%	34.545%
Maximum confidence	42.0%	42.857%	42.647%
Average confidence (%)	36.7715	36.9848	38.6551
standard deviation of confidence	3.0745	3.6034	3.4546
Mid-value of confidence	36.8035	36.3487	37.5000

, including the number of rules, minimum support and confidence, maximum support and confidence, mean percentage of support and confidence, the standard deviation percentage of support and confidence, and so on.

From the view of the rule number, both k = 8 and k = 9 can produce 12 rules, involving the relationship between multiple frequency components and speed as well as voltage. When the cluster number is 10, there are only five rules, and these five rules only involve three frequency components. Therefore, k = 10 is excluded. Then k = 8 and k = 9 are compared. From the perspective of the support level, their statistical indicators are very close, and their standard deviations are large too which means both of them are not centralized. From the point of confidence level, compared with k = 8, k = 9 has smaller minimum confidence, almost the same maximum confidence and a larger standard deviation. This indicates that considering rules with a confidence level, k = 9 has a higher confidence level than k = 8. Hence, k = 9 brings higher quality association rules.

4.1.2. The Adjacent Data Segments Correspondence (for Prediction)

When studying the factor influence of the previous data segment on the oscillation mode of the next data segment, the target data becomes the oscillation modes in the next segment. Input data is still the cluster tag. Like the analysis of the same segment, correlation analysis is done under different clustering numbers, namely k = 8, k = 9 and k = 10. After adjusting, the minsup is set as 6, and the minconf is 29. Results are shown in

Table 7. Association rules (the adjacent data segments correspondence).

k	No.	Preceding Item	Subsequent Item	Support (%)	Confidence (%)
8	1	45.37 Hz	cluster 4 & cluster 8	4.71464	47.3684
	2	12.41 Hz	cluster 4 & cluster 8	4.71464	42.1053
	3	23 Hz	cluster 4 & cluster 8	4.71464	42.1053
	4	23 Hz	cluster 4	18.1141	37.6712
	5	23 Hz	cluster 8	42.1836	37.0588
	6	45.37 Hz	cluster 8	42.1836	36.4706
	7	45.37 Hz	cluster 4	18.1141	35.6164
	8	23 Hz	cluster 7	9.8015	35.4430
	9	45.37 Hz	cluster 1	4.9628	35
	10	45.37 Hz	cluster 7	9.8015	32.9114
	11	45.37 Hz	cluster 5	4.2184	32.3529
	12	23 Hz	cluster 5	4.21836	32.3529
	13	45.37 Hz	cluster 3	6.2035	32
	14	23 Hz	cluster 3	6.2035	32
	15	12.41 Hz	cluster 6	10.67	31.3953
	16	23 Hz	cluster 1	4.9628	30
9	1	23 Hz	cluster 5	20.4715	38.7879
	2	23 Hz	cluster 3	37.7171	38.1579
	3	23 Hz	cluster 7	9.4293	36.8421
	4	45.37 Hz	cluster 4	6.9479	35.7143
	5	45.37 Hz	cluster 2	4.9628	35
	6	45.37 Hz	cluster 5	20.4715	33.9394
	7	45.37 Hz	cluster 7	9.4293	32.8947
	8	23 Hz	cluster 6	6.0794	32.6531
	9	45.37 Hz	cluster 3	37.7171	32.5658
	10	12.41 Hz	cluster 1	10.6700	31.3953
	11	45.37 Hz	cluster 6	6.0794	30.6122
	12	12.41 Hz	cluster 5	20.4715	30.3030
	13	23 Hz	cluster 2	4.9628	30
10	1	23 Hz	cluster 1	20.4715	38.7879
	2	23 Hz	cluster 5	8.43672	38.2353
	3	45.37 Hz	cluster 4	4.9628	35
	4	45.37 Hz	cluster 1	20.4715	33.9394
	5	45.37 Hz	cluster 5	8.4367	33.8235
	6	12.41 Hz	cluster 1	20.4715	30.3030
	7	12.41 Hz	cluster 6	10.6700	30.2326
	8	23 Hz	cluster 4	4.9628	30

.

The same comparison is given in

Table 8. Statistics comparison of association rules with different k values (the adjacent data segments correspondence).

Comparison Item	k = 8	k = 9	k = 10
Rule number	16	13	8
Minimum support	4.218%	4.963%	4.963%
Maximum support	42.184%	37.717%	20.471%
Average support (%)	12.2364	15.0315	12.3604
the standard deviation of support	12.5273	11.6484	6.9741
Mid-value of support	6.2035	9.4293	9.5533
Minimum confidence	30.0%	30.0%	30.0%
Maximum confidence	47.368%	38.788%	38.788%
Average confidence (%)	35.7407	33.7589	33.7902
the standard deviation of confidence	4.7163	2.9510	3.4930
Mid-value of confidence	35.2215	32.8947	33.8815

.

From the view of rule number, k = 10 produces the least number of rules and can be excluded; k = 8 can generate 16 rules, where the first three rules both have the previous item with two Clusters; k = 9 produces 13 association rules, less than k = 8, and the statistics of the rule confidence are all less than k = 8. Therefore, in the adjacent segment analysis, k = 8 brings higher quality association rules.

4.2. Association Rule Analysis of Wind Speed/Voltage Cluster And Oscillation Modes

Further analysis of the association rules between wind speed/voltage clusters and oscillation modes of wind generating sets is carried out with 1500 data segments. According to the analysis in Section Section 4.1.1, k = 9 is taken. The clustering results are shown in Figure 9.

The clustering result is basically consistent with 807 points. The cluster center parameters of these nine clusters are shown in

Table 9. Cluster center (k = 9).

Cluster	Wind Speed	V-A	V-B	V-C	Voltage Fluctuation
cluster 1	5.3710	2.2746	2.1476	2.1994	2.2072
cluster 2	4.1656	0.4119	0.3693	0.4125	0.3979
cluster 3	5.0864	2.7239	2.5004	2.5306	2.5850
cluster 4	2.1246	1.3252	1.2975	1.3173	1.3133
cluster 5	4.0849	1.1553	1.1468	1.1374	1.1465
cluster 6	4.4625	2.2289	2.1224	2.1684	2.1732
cluster 7	4.3226	1.4596	1.4068	1.4241	1.4302
cluster 8	3.2341	1.4214	1.3658	1.3975	1.3949
cluster 9	6.1592	2.4109	2.3131	2.3499	2.3580

. The clustering center will affect the result of clustering. In the subsequent analysis with more data segments, the initial values of the cluster center should be set consistently to achieve the same clustering effect.

The clustering results are transformed into tag data, and the final association input data is obtained. After the Apriori correlation analysis, the association rules are achieved and are shown in

Table 10. Association rules of 1500 data segments.

No.	Preceding Item	Subsequent Item	Support (%)	Confidence (%)
1	45.37 Hz	cluster 9	8.1142	41.6667
2	12.41 Hz	cluster 3	6.7618	41.1111
3	45.37 Hz	cluster 8	15.9279	40.0943
4	0.1–1.8 Hz	cluster 3	6.7618	36.6667
5	23 Hz	cluster 7	15.7776	35.7143
6	45.37 Hz	cluster 5	24.1172	35.2025
7	23 Hz	cluster 5	24.1172	34.5794
8	23 Hz	cluster 3	6.7618	34.4444
9	23 Hz	cluster 6	8.6401	33.9130
10	45.37 Hz	cluster 6	8.6401	33.0435
11	45.37 Hz	cluster 1	13.7491	32.2404
12	23 Hz	cluster 1	13.7491	30.6011
13	23 Hz	cluster 9	8.1142	30.5556
14	45.37 Hz	cluster 7	15.7776	30.4762

.

As Table 10 indicates, the association rules are mainly concentrated in the three modes: 45.37 Hz, 23 Hz and 12.41 Hz. In the correlation analysis results, there is no association rule of 1.92 Hz, 79 Hz and 4.37 Hz. It shows that in the output power of the wind generating sets, the oscillation components of these three frequencies occupy less.

Among the 14 association rules, rule “cluster 9$\to$45.37 Hz” has the maximum confidence level which is 41.67%. According to the clustering results, the “cluster 9” has the characteristics of 5.5~6.75 m/s wind speed and 2.0~2.6 V voltage fluctuation. This rule indicates that the wind speed and voltage fluctuation cluster will rapidly cause the 45.37 Hz frequency component, and the probability of occurrence is over 40%. The confidence level of the rule “cluster 3$\to$12.41 Hz” ranks the second, 41.11%. The clustering results show that the “cluster 3” has the characteristics of high voltage fluctuation and 4~5.75 m/s wind speed. The rule states that such a combination will quickly lead to a 12.41 Hz frequency component, and the probability of occurrence is over 40%. The confidence level of the rule “cluster 8$\to$45.37 Hz” also reaches over 40%. According to the clustering results, the “cluster 8” has the characteristics of 1~1.8 m/s voltage fluctuation and the 2.5~3.5m/s wind speed. The rule states that such a combination will quickly cause the 45.37 Hz frequency component, and the probability of occurrence is up to 40%. Meanwhile, the rules with anterior “cluster 4” with the characteristics of the wind speed less than 2.5 m/s, voltage fluctuation among 1~1.6 m/s never show up in the result.

4.3. Prediction of Oscillation Mode Based on the Apriori Algorithm

To predict the oscillation mode, input becomes the combination of the clustering tag data in the previous data segment corresponding to the oscillation frequency tag segment in the next. 1500 data segments are taken for analysis. According to the above analysis in 4.1.2, k is given the value of 8, and the clustering result is shown in Figure 10.

The clustering result is consistent with 807 points. Among all the clusters, cluster 2 is the largest and cluster 4 is the smallest, which is different from the result in part A above because different cluster centers are selected. When cluster centers are chosen like Figure 10, the elements of cluster 4 can be considered as outliers and will be ignored by the minimum support condition in the correlation analysis.

The cluster center parameters of these 8 clusters are shown in

Table 11. Cluster center (k = 8).

Cluster	Wind Speed	V-A	V-B	V-C	Voltage Fluctuation
cluster 1	2.42045	2.28851	2.30949	2.33949	6.04808
cluster 2	1.25799	1.23799	1.23884	1.24494	4.14762
cluster 3	2.24225	2.14732	2.20835	2.19931	5.17199
cluster 4	0.26148	0.2329	0.27851	0.25763	5.67557
cluster 5	2.68967	2.48604	2.52175	2.56582	4.97684
cluster 6	1.38416	1.33245	1.36456	1.36039	2.92717
cluster 7	2.00854	1.87115	1.91066	1.93011	4.14033
cluster 8	0.46793	0.41485	0.44918	0.44399	3.90241
cluster 9	2.42045	2.28851	2.30949	2.33949	6.04808

. In this part, the cluster center will affect the result of the cluster which means it also affects the final mode judgment. Therefore, when the association rules are applied to oscillation mode prediction, initial values of the cluster center must be consistent with the training condition to achieve the same clustering effect.

The clustering result is tag-converted to obtain the final associated input data. After correlation analysis, the association rules are shown in

Table 12. Association rules of 1500 data segments (the adjacent data segments correspondence).

No.	Preceding Item	Subsequent Item	Support (%)	Confidence (%)
1	45.37 Hz	cluster 8	15.9398	41.5094
2	23 Hz	cluster 5	24.1353	37.3832
3	45.37 Hz	cluster 5	24.1353	34.2679
4	45.37 Hz	cluster 6	8.6466	33.9130
5	23 Hz	cluster 6	8.6466	33.9130
6	23 Hz	cluster 7	15.7895	33.8095
7	12.41 Hz	cluster 1	13.7594	32.7869
8	23 Hz	cluster 1	13.7594	30.6011
9	12.41 Hz	cluster 7	15.7895	30.4762
10	23 Hz	cluster 3	6.6917	30.3371
11	45.37 Hz	cluster 7	15.7895	29.5238

.

From the results in Table 12, the wind speed and voltage fluctuation of the previous data segment mainly affect partial oscillation modes of the next data segment, including 45.37 Hz, 23 Hz, and 12.41 Hz. As the same with the result in the same data segment analysis, the wind speed and voltage fluctuation of the previous data segment are irrespective with mode 1.92 Hz, 79 Hz, and 4.37 Hz of the next data segment. Different from the same data segment analysis result, the association between the wind speed and voltage of the previous data segment and the low-frequency oscillation mode of the next data segment is weakened, indicating that the two factors have less influence on the low-frequency oscillation mode of the next data segment.

The support degree is related to the number of clusters, so we use it only as a threshold for rule screening. The analysis of rules mainly depends on the confidence level. Among all the rules, rule “cluster 8$\to$45.37 Hz” has the highest confidence level of 41.5%.

As can be seen from Figure 10, the wind speed of the cluster 8 is between 3.2 m/s and 4.5 m/s, and the voltage fluctuation is low. Meanwhile, the mode 45.37 Hz is a SSCI mode, which means the controller acts to stable the output power but at the same time interacts with the fixed series compensation, resulting in the SSCI mode in the next data segment.

Then, 200 data segments are selected to predict the three modes of 45.37 Hz, 23 Hz, and 12.41 Hz. These 200 points are clustered in the same cluster center of Table 10. Most of these points belong to clusters 2, 3, 6, and 7. Rules 4, 5, 6 and 9, 10, 11 can be extracted from Table 11 as the oscillation mode prediction result, namely “cluster 6$\to$45.37 Hz”, “cluster 6$\to$23 Hz”, “clustering” 7$\to$23Hz”, “cluster 7$\to$12.41Hz”, “cluster 3$\to$23Hz”, “cluster 7$\to$45.37 Hz”. The confidence levels of these six rules are taken as the predicted value, which means that when the previous item occurs, the occurrence probability of the latter item is the corresponding confidence value. Prony analysis is performed on the actual power curve of the 200 data segments to obtain the actual oscillation modes. The actual value is the segment number percentage. Statistical prediction errors are obtained in

Table 13. Confidence level analysis of prediction and reality.

No.	Preceding Item	Subsequent Item	Predict Confidence (%)	Actual Confidence (%)	Error
1	23 Hz	cluster 6	33.91	38.98	5.07
2	45.37 Hz	cluster 7	29.52	36.97	7.45
3	23 Hz	cluster 3	30.34	33.33	2.99
4	45.37 Hz	cluster 6	33.91	32.20	−1.71
5	23 Hz	cluster 7	33.81	28.57	−5.24
6	12.41 Hz	cluster 7	30.48	26.89	−3.59

.

Figure 11 is a line graph comparing the confidence level of predicted results and practical results.

From the prediction results, the maximum confidence level error between the predicted value and the actual value does not exceed 8%, and the association rules related to the clustering results of 200 predicted data segments are all confirmed, indicating that prediction rules obtained by training 1500 data segments are already highly credible. Among them, the rule “cluster 6$\to$45.37 Hz” has the smallest error, which means the probability that the wind speed/voltage combination of cluster 6 induces the 45.37 Hz mode is very close to 0.3391; the rule “cluster 7$\to$45.37 Hz” has the largest error, indicating that the probability that the wind speed/voltage combination of the cluster 7 induces the 45.37 Hz mode is around 0.2952. The prediction and actual confidence percentage here are statistical values. As the sample size increases, the statistical value will be close to the probability value, and the prediction result will have higher credibility.

5. Conclusions

In this paper, association analyzing model of correlation between wind speed/voltage fluctuation clusters and oscillation modes is established. The traditional power signal processing method is combined with a data mining algorithm to mine association rules between the oscillation modes and main influencing factors, using metered data of wind generating sets. The conclusions are as follows.

• The association rules between clusters and oscillation modes can be obtained by analyzing the metered data via improved Apriori algorithm. The rules are denoted by “Wind speed/voltage fluctuation clustering$\to$oscillation mode”. The higher the confidence level of an association rule is, the greater the probability of corresponding oscillation modes occurrence is.
• In association rule analysis, support level does not need to be set too high. Low support and high confidence can reflect the strong correlation between a cluster and the corresponding mode. Even when the cluster contains few elements, it is also easy to cause the corresponding oscillation mode in the power.
• Wind speed/voltage fluctuation cluster number has a great influence on association rules. Optimal cluster number corresponds to highest support and confidence level. The results of correlation analysis show that different clusters can lead to different oscillation components, and large voltage fluctuation may quickly induce SSCI component in power.
• The association rule of adjacent data segments can be used to predict the oscillating mode of the wind generating sets. The error between the prediction result and the actual situation is small, indicating that the confidence level is very close to the probability value. As the sample capacity increases, the statistical value will be close to the probability value, and the prediction result will be more credible.

Based on the result, it is possible to directly judge whether there is an oscillation mode under the corresponding conditions directly from the clustering category of voltage fluctuation and wind speed, which provides convenience for the monitor of the wind farm. Besides, the proposed correlation analysis model is also universal and can also be used to analyze oscillation problems of other systems, or harmonic problems, which means the model has a certain reference value for the scientific community too.