1. Introduction
The safety and reliability of power transformers, which are the core pieces of equipment in a power grid, are important for the reliable operation of the entire power grid [
1]. Foreign statistics show that approximately 2% of transformers that run continuously for more than four years will experience accidents of varying degrees [
2]. The high failure rate of transformers has always affected the safe and stable operation of the power grid [
3], and it is not difficult to find that mechanical faults in transformer are often due to latent issues upon reviewing historical cases of transformer accidents [
4]. Transformer faults generally involve the failure of main components and accessories, with the primary source of these faults being due to windings and core failures. In China, faults have occurred in 18 transformers in and above the 110 kV class [
5]. Of these faults, 10 (55.6%) were caused by winding issues. From 2006 to 2010, the State Grid Corporation of China (SGCC) compiled statistics on the causes of faults in 46 transformers, of which 26 (56.5%) were caused by winding deformation [
6]. In 2013, there were five accidents in transformers of the 110 kV class and above belonging to the Guangxi Power Supply Company of the Southern China Power Grid [
7]. Of these, four cases (80%) were caused by winding deformation.
The study of electromagnetic vibration in transformers began in the 1920s, mainly by large power-transformer manufacturers and related research institutions. However, that work was limited by the technology available at that time, when winding fault simulations were not ideal [
8]. Fahnoe H. studied the forced vibration of a transformer’s vibrating iron core under magnetostriction and resonance at the harmonic frequency [
9]. A substantial amount of simulation of the transformer was carried out. The modal-resonance frequency of the transformer was analyzed such that the transformer avoided resonance, but the simulation results were not verified via experimentation [
10]. Foster S. L. and others used finite element numerical analysis to calculate the electromagnetic field and structural force field of large transformers, and obtained the vibration of the transformer core [
11]. By combining electromagnetic-field theory with the theory of structural mechanics, Yang Qingxin and other scholars in China established a mathematical model of the electromagnetic vibration of the iron core of a power transformer [
12,
13,
14]. The model was used to simulate magnetostriction of silicon steel sheets. On this basis, the distribution of the sound field around the core was analyzed. These researchers paid considerable attention to the vibration of the iron core, but the vibration of the windings at various working conditions was less important to them. Liu Dichen and other scholars established an electromagnetic mechanical sound field finite-element model of a transformer core and its winding [
15]. In ANSYS Workbench, a finite-element model of the transformer winding, iron core, and oil tank were established. Transient electromagnetic-field analysis was used to obtain the alternating electromagnetic force of the transformer core and winding under the effect of alternating currents. Noise distribution was analyzed, but little attention was paid to the spectrum analysis of the windings under various fault conditions. Ji Shengchang and other scholars discussed in detail the relationship between the vibration of the winding, the iron core, the load current, and the no-load voltage, and proposed a method for extracting the characteristics of the vibration signal of the transformer based on wavelet analysis [
16,
17]. Through simulation and experimentation, Yu Xiaohui and others discussed the interaction between the tightening force and the natural frequency of the winding and concluded that the pretension of the windings can change their natural frequency [
18]. A comprehensive analysis of the research conducted by experts around the world reveals that, although many effective diagnostic methods based on vibration signals have been proposed, there still exist problems, such as incomplete simulations of the various types of winding faults and poor diagnostic accuracy.
In recent years, various nondestructive testing methods for transformer-winding deformation have been developed, such as the frequency-response analysis method for comparing transformer frequency-response changes, and vibration analysis method for judging winding state based on the transformer-vibration signal. The principle of frequency-response analysis is to detect the amplitude-frequency response characteristics of each winding of the transformer, and compare the detection results horizontally or vertically. According to the difference of amplitude-frequency response characteristics, winding faults that may occur in the transformer are comprehensively judged. In recent years, scholars have paid more and more attention to vibration-detection transformer research. The vibration-analysis method discriminates the winding state of the transformer by detecting the vibration signal transmitted to the body surface [
19,
20]. The principle is to reflect the winding states by detecting a change in the mechanical characteristics of the winding. The frequency-response method has many factors that affect the test results, such as the position of the signal source, the length of test leads, the length of the test instrument grounding wire, the position of the transformer tap changer, and connection mode. Compared with the frequency-response method, the vibration-analysis method has fewer factors affecting the test results. The noise of the transformer cooling system will pollute the vibration signal. When collecting the signal, it should be as far away from the fan group as possible, or you should take noise-reduction measures. The vibration test results of transformer-winding deformation are affected by the vibration of the core. Power frequency 150 Hz and 250 Hz components appear in the frequency spectrum of transformer-vibration signals under a three-phase asymmetric operation. The severe overvoltage generated in the asymmetric phase increases the amplitude of the resonant frequency of the core, which interferes with the test results of winding. When a short-circuit fault occurs, the vibration of the iron core is far less than that of winding, and it can be approximated that the detected vibration contains only vibration signals of the winding. The frequency-response method is blackout detection, while the vibration-detection method is live detection [
21,
22]. It can continuously monitor transformer-winding deformation and reflect the decline trend of transformer short-circuit resistance after repeated short-circuit shocks, which reduces the difficulty of online monitoring and fault diagnosis of the power transformer.
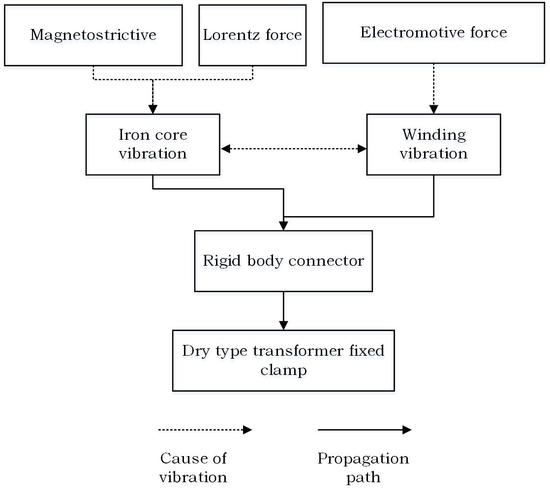
Because the vibration of the transformer is a complicated process, the interaction between the magnetic field and the load current, as well as between the magnetostriction of the silicon steel sheet and the structural change in the transformer, produce changes in the vibration signal in both the time and frequency domains, thus increasing the difficulty in fault monitoring and diagnosis. In this paper, the SCB10-1000/10 dry-type transformer is studied in detail from the perspective of simulation modeling, fault simulation, and feature analysis to obtain state diagnostics on transformer winding via vibration analysis. Based on the mechanical-vibration characteristics of dry-type transformer windings, a short-circuit experiment was performed on the SCB10-1000/10 transformer, and the vibration signals at its surface were measured. A vibration-simulation model of the SCB10-1000/10 transformer was established using COMSOL Multiphysics 5.3, and the coupling calculations were performed with regard to the circuit, magnetic field, and solid mechanics of the transformer, among other areas of physics. By comparing the simulated data to the actual data of the transformer, the accuracy of the model was proven. Using this model, faults like loosening, deformation, and loss of insulation from the transformer windings were simulated, and the vibration characteristics of the winding fault were subsequently analyzed. The model utilizes multiphysical field-coupling simulation of the electromagnetic solid mechanics of dry transformer windings, which can provide a new basis for the state simulation and fault diagnosis of transformer windings.
3. Multiphysical Field-Coupling Model for Winding Vibration of Dry-Type Transformer
In this paper, COMSOL Multiphysics software was used to simulate the vibration of the SCB10-1000/10 dry-type transformer winding, and coupling simulation analysis of the magnetic field and the solid mechanics was performed.
3.1. Establishment and Mesh Generation of a Vibration-Simulation Model for a Dry-Type Transformer
The structure of the transformer is complex and includes a variety of components such as the winding, iron core, and cooling device. For the purpose of the simulation, the transformer is simplified and treated as an ideal model in which the internal cooling device and supporting fastening components are neglected. The finite-element geometric model was set up based on the actual structural parameters of the SCB10-1000/10 dry-type transformer (Xuzhou Debon Electric Equipment Co., Ltd., Xuzhou, China), and a fixed constraint was applied at both ends of the winding to simulate clamping. To simulate the electrical insulation of the actual transformer, three-phase high- and low-voltage winding turns and layers were used, which allowed the electromagnetic field to be solved. The solid mechanics model was set up as a fully coupled solution to understand the connection between the differential equation of motion and the differential equation of the electromagnetic field. The simulation model is shown in
Figure 4a. To improve efficiency, the geometric transformer model was simplified by considering it symmetric.
Figure 4b illustrates the simplified geometric model of the body.
The geometric model of the transformer is meshed by means of a free tetrahedron network, and the mesh model shown in
Figure 5a can be obtained. The mesh quality is shown in
Figure 5b, and the closer the value is to 1, the higher the mesh quality is. The winding and core structural parameters of the SCB10-1000/10 dry-type transformer are shown in
Table 2 and
Table 3.
3.2. Simulation Model of Electromagnetic Field
Figure 6 shows the circuit diagram of the transformer. In the diagram, an AC voltage source with a 50 Hz frequency was applied to the three-phase high-voltage side, and the low-voltage side was short-circuited. A 50 Hz AC voltage to the rated current was applied to the high-voltage winding by an external voltage source. The three-phase induction current of the low-voltage winding was obtained by electromagnetic-coupling calculation, as shown in
Figure 7. As a result, the amplitude of the three-phase induction current of the low-voltage winding was 2041 A, and its effective value was 1443.38 A. The simulation results are consistent with the rated current of the transformer, as shown in
Table 1.
The current obtained from the circuit module is used as the excitation source of the magnetic-field model, and current density
J was brought into the magnetic-field differential equation as follows:
In Equation (7),
μ0 represents the permeability of free space and has a value of 4
π *10
−7H/m,
R is the relative permeability,
A is the vector magnetic potential, and
Je is the current density. Additionally, the following relationship exists in the electromagnetic-field model:
where
B represents the magnetic-flux density, and
H represents the magnetic-field intensity.
Figure 8 shows the H–B curve of the transformer when it is in operation. The curve in
Figure 8 also provides information on the material properties of the dry-type transformer core, which agrees with the actual material properties of the transformer.
The magnetic-flux density distribution around the winding and the core of the dry-type transformer during a short-circuit test was obtained by coupling the electromagnetic-field model.
As seen from
Figure 9, the maximum flux-leakage density of the dry-type transformer winding was 0.08 T, and the maximum flux density of the core was 1.75 T. The results of the simulation are in line with the output parameters of the SCB10-1000/10 dry-type transformer. The results verify the correctness of the model, demonstrating that the model can be further used for the simulation of various faults in the windings.
3.3. Modeling of Solid Mechanics and Analysis of Winding Vibration
In the solid-mechanics model, the vibration characteristics of the dry-type transformer winding must be coupled. The mass inertia, elasticity, and damping of the winding are the key factors affecting its vibration. Equation (9) provides the differential equations of motion for the solid mechanics.
In Equation (9), Mi represents the mass matrix; Ci represents the damping coefficient matrix, represents the stiffness coefficient matrix, z represents the deformation (displacement) of the winding, represents the deformation velocity of the winding, represents the deformation acceleration of the winding, and f(t) represents the magnitude of the force on the winding. Equation (5) for electrodynamic force is incorporated into the differential equation of Motion (9).
To converge to a solution, it is necessary to impose fixed constraints on both ends of the transformer winding.
In Equation (10), mass matrix
Mi, damping coefficient
Ci, and stiffness coefficient
ki are all constant, which makes it a constant coefficient differential equation. The solution of the equation is composed of the general solution and the special solution. For the homogeneous part,
the general solution is as follows:
In Equation (12),
Y and
θ are constants whose values are determined by the initial conditions, and
represents the natural frequency of the vibration of the transformer winding, which is expressed as follows:
There are two special solutions for Equation (10):
In the equation: .
The total displacement of the transformer winding at any time can be expressed as follows in Equation (16):
where
t, the total displacement of the winding, and the displacement velocity are zero. Integral constants
Y and
θ can then be obtained.
By quadratic derivation of the total displacement equation of the transformer winding, the vibration acceleration
a of the transformer winding at any time
t can be obtained as in Equation (17):
From the solution above, it can be seen that the vibration characteristics of a given transformer’s windings are mainly related to the elastic coefficient and the winding geometry, that is, when elastic coefficient
K and the geometric structure of the transformer winding are changed, the vibration acceleration of the transformer-winding surface changes accordingly.
Table 4 shows the main material properties of the winding and the core in the solid mechanics model [
29].
The amplitude and axial forces on the transformer winding are obtained through a simulation of the solid mechanics, as demonstrated in
Figure 10. The legend shows the magnitude of stress, and the red arrows indicate the direction of force. As seen in
Figure 10a, the external high-voltage windings receive outward traction, while the inner low-voltage windings are pushed inward; the force of the outer winding is obviously lower than that of the inner winding.
Figure 10b shows that the two ends of the transformer winding are subjected to inward extrusion pressure. Therefore, the above simulation results are in line with the actual force on the transformer windings.
To further verify the accuracy of the above model, the vibration signals measured by the transformer short-circuit test were compared with the vibration signals from the simulation.
Figure 11 shows the layout of the actual vibration-signal measurement points and the simulation-model measurement points. The locations in the simulation model are consistent with the vibration signal measured in the experiment.
Figure 12 shows the calculated results of vibration at the placement of the acceleration vibration sensor and the measured results. Because the current passing through the winding in the short-circuit experiment is rated current, the simulation-calculation conditions are close to the actual measurement conditions. As shown in
Figure 12, the simulation results are in good agreement with the measured results, which further illustrates the validity of the finite-element model and the correctness of the calculation results. In addition, the vibration waveform of the test point appears in the shape of the top cusp, which may be due to the material characteristics [
30].
5. Conclusions
In this paper, the mechanical-vibration characteristics of transformer windings were studied theoretically. Changes in the mechanical state of the windings were reflected in their vibration signals. A simulation model of vibration was established for an SCB10-1000/10 dry-type transformer winding using COMSOL software, and a multifield-coupling simulation of the circuit, magnetic field, and solid mechanics was performed. The following conclusions were obtained through simulation and experimental analysis. By changing the geometry model and power parameters, similar conclusions can be obtained for other types of dry-type transformers, which can be extended to the study of winding-vibration characteristics of various types of dry-type power transformers. For the oil-immersed transformer, the simulation model was greatly changed, so it was necessary to add an oil-tank wall to the transformer model, replace the medium with insulation oil, and consider the vibration-signal propagation process in the insulation oil. At the same time, we also studied the occurrence and propagation of the winding vibration of oil-immersed transformers. Because the oil-immersed transformer was closed, the vibration-signal sensor could only be mounted on the wall of the oil tank. When analyzing the signal received by the vibration-signal sensor, we needed to consider the properties of the different insulating oil. Therefore, the vibration analysis in this paper was limited to dry-type transformers.
(1) A short-circuit experiment was performed on an SCB10-1000/10 transformer, which is a dry-type transformer. Information on the vibration acceleration at the surface of the transformer was obtained using a vibration-acceleration sensor (YD70C), a charge amplifier (DHF-10), and a Tek oscilloscope. Vibration-signal analysis showed that, when the secondary winding of the transformer was short-circuited, the signal was mainly composed of a 100 Hz component and contained relatively small components at 50 Hz, 200 Hz, and 300 Hz.
(2) Based on the vibration data obtained from the transformer short-circuit experiment, a multiphysical field-coupling vibration-simulation model of the dry-type transformer winding is established using the parameters of the actual transformer. The vibration-acceleration signal was obtained from actual measurement points, which was then compared to the corresponding points in the simulation. The similarity between the two exceeded 80%. Therefore, the model can be used to investigate the vibration of transformer windings and possesses high value in engineering applications.
(3) Based on the simulation model, for normal working conditions, fault simulations of the transformer windings were carried out. Specifically, winding loosening, deformation, and insulation shedding were simulated, and the vibration characteristics of these winding faults were analyzed. When insulation was shed, the amplitude in the frequency domain at 100 Hz, 200 Hz, and 300 Hz increased. When the winding was loose, the maximum amplitude in the frequency domain appeared at 200 Hz, and the amplitude at 300 Hz was also relatively larger. When winding deformation occurred, the maximum amplitude of the vibration signal occurred at 300 Hz, and the amplitude at 200 Hz exceeded the amplitude at 100 Hz. The simulation results are consistent with the experimental results, which verify the accuracy of the fault model. This method can provide a new basis for simulating and diagnosing transformer-winding faults.