DNN-Assisted Cooperative Localization in Vehicular Networks
Abstract
:1. Introduction
2. Problem Formulation
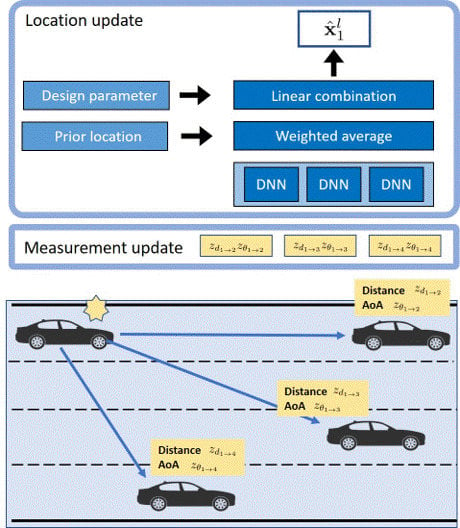
3. Deep Learning-Based Approach in Cooperative Localization
3.1. DNN Architecture
3.2. Algorithm Structure
| Algorithm 1 Proposed cooperative localization via deep neural network (DNN). |
|
4. Simulation and Discussions
4.1. Dataset for Training the DNN
4.2. Performance Evaluation of Trained DNN
4.3. Performance of DNN-Assisted Cooperative Localization
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Closas, P.; Fernandez-Prades, C.; Fernandez-Rubio, J.A. Maximum Likelihood Estimation of Position in GNSS. IEEE Signal Process. Lett. 2007, 14, 359–362. [Google Scholar] [CrossRef] [Green Version]
- Patwari, N.; Ash, J.N.; Kyperountas, S.; Hero, A.O.; Moses, R.L.; Correal, N.S. Locating the nodes: Cooperative localization in wireless sensor networks. IEEE Signal Process. Mag. 2005, 22, 54–69. [Google Scholar] [CrossRef]
- Gustafsson, F.; Gunnarsson, F. Mobile positioning using wireless networks: Possibilities and fundamental limitations based on available wireless network measurements. IEEE Signal Process. Mag. 2005, 22, 41–53. [Google Scholar] [CrossRef]
- Kim, S.; Brown, A.P.; Pals, T.; Itlis, R.A.; Lee, H. Geolocation in ad hoc networks using DS-CDMA and generalized successive interference cancellation. IEEE J. Sel. Areas Commun. 2005, 23, 984–998. [Google Scholar] [CrossRef]
- Wymeersch, H.; Lien, J.; Win, M.Z. Cooperative localization in wireless networks. IEEE Proc. 2009, 97, 427–450. [Google Scholar] [CrossRef]
- Loeliger, H.A. An introduction to factor graphs. IEEE Signal Process. Mag. 2004, 21, 427–450. [Google Scholar] [CrossRef]
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.A. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Baron, D.; Sarvotham, S.; Baraniuk, R.G. Bayesian Compressive Sensing Via Belief Propagation. IEEE Trans. Signal Process. 2010, 58, 269–280. [Google Scholar] [CrossRef]
- Cakmak, B.; Urup, D.N.; Meyer, F.; Pedersen, T.; Fleury, B.H.; Hlawatsch, F. Cooperative localization for mobile networks: A distributed belief propagation–mean field message passing algorithm. IEEE Signal Process. Lett. 2016, 23, 828–832. [Google Scholar] [CrossRef]
- Meyer, F.; Hlinka, O.; Hlawatsch, F. Sigma Point Belief Propagation. IEEE Signal Process. Lett. 2014, 21, 145–149. [Google Scholar] [CrossRef]
- García-Fernández, Á.F.; Svensson, L.; Särkkä, S. Cooperative Localization Using Posterior Linearization Belief Propagation. IEEE Trans. Veh. Technol. 2018, 67, 832–836. [Google Scholar] [CrossRef]
- Kim, S.; Lee, S.H.; Kim, S. Cooperative localization with distributed ADMM over 5G-based VANETs. IEEE WCNC 2018. [Google Scholar] [CrossRef]
- Kim, H.; Choi, S.W.; Kim, S. Connectivity Information-aided Belief Propagation for Cooperative Localization. IEEE Wirel. Commun. Lett. 2018, 7, 1010–1013. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Tan, Z.H.; Zhang, Y.; Ma, Z.; Guo, J. DNN Filter Bank Cepstral Coefficients for Spoofing Detection. IEEE Access 2017, 5, 4779–4787. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, H.; Ren, Y.; Han, Z.; Chen, K.; Hanzo, L. Machine Learning Paradigms for Next-Generation Wireless Networks. IEEE Wirel. Commun. 2017, 24, 98–105. [Google Scholar] [CrossRef]
- Ye, H.; Liang, L.; Li, G.Y.; Kim, J.; Lu, L.; Wu, M. Machine Learning for Vehicular Networks: Recent Advances and Application Examples. IEEE Veh. Technol. Mag. 2018, 13, 94–101. [Google Scholar] [CrossRef]
- Li, J.; Mei, X.; Prokhorov, D.; Tao, D. Deep Neural Network for Structural Prediction and Lane Detection in Traffic Scene. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 690–703. [Google Scholar] [CrossRef] [PubMed]
- Win, M.Z.; Conti, A.; Mazuelas, S.; Shen, Y.; Gifford, W.M.; Dardari, D.; Chiani, M. Network localization and navigation via cooperation. IEEE Commun. Mag. 2011, 49, 56–62. [Google Scholar] [CrossRef]
- Sze, V.; Chen, Y.H.; Yang, T.J.; Emer, J.S. Efficient Processing of Deep Neural Networks: A Tutorial and Survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, A.G.; Fernandes, D.; Catarino, A.P.; Monteiro, J.L. Performance Analysis of ToA-Based Positioning Algorithms for Static and Dynamic Targets with Low Ranging Measurements. Sensors 2017, 17, 1915. [Google Scholar] [CrossRef] [PubMed]
- Akail, N.; Moralesl, L.Y.; Murase, H. Reliability Estimation of Vehicle Localization Result. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 740–747. [Google Scholar]
- Zhang, W.; Liu, K.; Zhang, W.; Zhang, Y.; Gu, J. Deep Neural Networks for wireless localization in indoor and outdoor environments. Neurocomputing 2016, 194, 279–287. [Google Scholar] [CrossRef]
- Adege, A.B.; Yen, L.; Lin, H.P.; Yayeh, Y.; Li, Y.R.; Jeng, S.S.; Berie, G. Applying Deep Neural Network (DNN) for large-scale indoor localization using feed-forward neural network (FFNN) algorithm. In Proceedings of the 2018 IEEE International Conference on Applied System Invention (ICASI), Chiba, Japan, 13–17 April 2018; pp. 814–817. [Google Scholar]
- Nguyen, T.; Jeong, Y.; Shin, H.; Win, M.Z. Machine Learning for Wideband Localization. IEEE J. Sel. Areas Commun. 2015, 33, 1357–1380. [Google Scholar] [CrossRef]
- Ihler, A.T.; Fisher, T.; Moses, R.L.; Willsky, A.S. Nonparametric belief propagation for self-localization of sensor networks. IEEE J. Sel. Areas Commun. 2005, 23, 809–819. [Google Scholar] [CrossRef]
- Dai, W.; Shen, Y.; Win, M.Z. Energy-Efficient Network Navigation Algorithms. IEEE J. Sel. Areas Commun. 2015, 33, 1418–1430. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]





| Parameter | Value |
|---|---|
| Batch size | 100 |
| Learning rate | 0.001 |
| The number of hidden layers | 3 |
| The number of nodes at k-th hidden layer | 32 |
| The number of nodes at input layer | 2 |
| The number of nodes at output layer | 2 |
| Regularization strength | 0.001 |
| Activation Function | ReLU, Linear |
| Optimizer | Adam |
| epoch | 10 |
| Distance measurement error | 1 m |
| AoA measurement error | 1 |
| Number of Vehicles I | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| DNN | 1.306 × | 2.176 × | 3.264 × | 4.570 × | 6.093 × | 7.834 × |
| SPAWN | 7.505 | 1.251 | 1.877 × | 2.628 × | 3.505 × | 4.507 × |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eom, J.; Kim, H.; Lee, S.H.; Kim, S. DNN-Assisted Cooperative Localization in Vehicular Networks. Energies 2019, 12, 2758. https://doi.org/10.3390/en12142758
Eom J, Kim H, Lee SH, Kim S. DNN-Assisted Cooperative Localization in Vehicular Networks. Energies. 2019; 12(14):2758. https://doi.org/10.3390/en12142758
Chicago/Turabian StyleEom, Jewon, Hyowon Kim, Sang Hyun Lee, and Sunwoo Kim. 2019. "DNN-Assisted Cooperative Localization in Vehicular Networks" Energies 12, no. 14: 2758. https://doi.org/10.3390/en12142758
APA StyleEom, J., Kim, H., Lee, S. H., & Kim, S. (2019). DNN-Assisted Cooperative Localization in Vehicular Networks. Energies, 12(14), 2758. https://doi.org/10.3390/en12142758