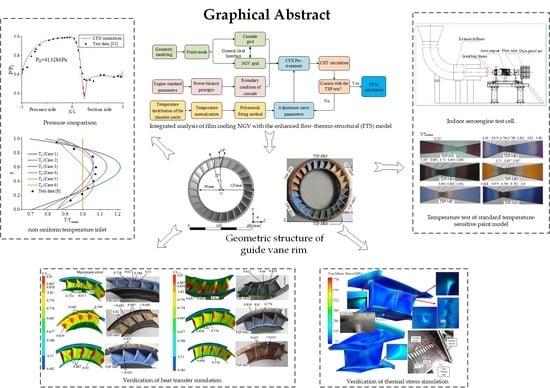
1. Introduction
With the development of aeronautical technology, turbine inlet temperature reaches to 2000 K which exceeds the melting point of high-temperature metal materials. It is necessary for the normal operation of turbine components to apply cooling measurement [
1]. By adopting turbine cooling technology, it is possible to reduce average temperature away from rupture strength and temperature gradient to decrease thermal stress level. In term of the estimation of temperatures on turbine components based on engineering practices, thermal fatigue life of nozzle guide vane (NGV) is very sensitive to temperature. Therefore, it is urgent to find an efficient approach to accurately predict the temperature of turbine guide vane.
With the development of conjugate heat transfer (CHT) technology, the aerodynamic heat transfer of NGV is attracting the attention of numerous researchers. Funazaki [
2] studied the cooling effectiveness at the leading edge of turbine front stages using the CHT calculation technique. Maheu [
3] and Liu [
4] discussed the heat transfer performance of a low-Mach turbine blade and heat transfer problem of a typical film cooling blade by ANSYS-CFX software. However, it is a large challenge for the design of turbine devices, especially NGV, owing to the non-uniform temperature profiles of turbine inlet (combustor outlet). To investigate the interacting influences between total pressure and temperature radial gradients on heat transfer performance of a high-pressure turbine vane, Barringer et al. [
5,
6] developed a combustor simulator and revealed pressure gradient seriously influencing vane heat transfer [
7]; Povey et al. [
8] also simulated the engine combustor exit realistic temperature profiles. The subsequent studies revealed the influences of hot spot on the heat transfer of both NGV and intermediate pressure vanes [
9]. Wang et al. [
10] pointed out that the migration path of hot streak in vane passage was influenced by the vortices. The above works demonstrated that the passage vortex extended the radial migration of fluids and induced higher temperature. However, the influence of film cooling holes on the temperature of NGV was not focused on. The investigation of NGV aerodynamic heat transfer problems by CHT technology is promising to give an exact temperature for thermal structure analysis.
One point causing the thermal fatigue of NGV is non-uniform temperature environment. Recently, based on FTS coupling technology, the influence of non-uniform temperature field on thermal strength performance of NGV was widely researched [
11,
12], and some studies about NGV life prediction also emerged. Kim et al. studied convective heat transfer coefficients and stresses on blade surfaces using finite volume (FV) and finite element (FE) methods [
13], showed the maximum material temperature and thermal stress at the trailing edge near the mid-span, and discussed the life prediction methods of turbine components by coupling aero-thermal simulation with a nonlinear deformation thermal-structural FE model and a slip-based constitutive model [
14]. Chung [
15] predicted cracks on the vane of a power generation gas turbine by the FTS method.
The other point is film cooling technology which may lead to thermal stress concentration. The purpose of film cooling technology is to reduce the working temperature of NGV material [
16]. This technology was also one of the hotspots in the research of aeroengine cooling technology in recent years [
17]. Elnadya et al. [
18] studied the cooling effectiveness of expanded holes on the leading edge of NGV and found that the cooling effectiveness of a cooling hole was proportional to blowing ratio, and the stress at the hole edges varied smoothly. Moritz et al. [
19] studied film cooling holes at the leading edge of NGV by thermal-fluid coupling calculations. Kim et al. [
20] and Nowak et al. [
21] optimized the hole-structure to some extent and reduced the maximum temperature load with regard to the influences of porosity, passage, jet angle, and arrangement on film cooling effectiveness. In fact, however, the maximum temperature is not the sole factor of determining NGV service life. Thermal stress concentration caused by concentrated cooling in holes was validated to also be a key factor of determining NGV service life [
22]. A large temperature gradient might lead to thermal fatigue and thus should be considered in the design process [
23,
24]. In this case, thermal stress was further discussed and controlled by cooling technology [
25,
26].
Briefly, in the design process of an NGV, it is unsatisfactory to only consider heat transfer performance or thermal strength. The concept of high-integrity was proposed by the United States Air Force in 2012, for numerical simulation of NGV cooling structure [
27]. High-integrity requires the consistency of numerical simulation with a real structure. Due to excess computational loads, however, we have not found related works investigating the high-integrated NGV simulation so far.
This paper attempts to develop an enhanced flow-thermo-structural model to improve the integrated analysis of film cooling NGV in computing accuracy, by regarding non-uniform inlet temperature. In the enhanced model, an efficient turbulence model (i.e., shear-stress-transport model (SST γ-θ model)) and weak spring approach are utilized and the temperature test data of combustor are referenced in constraint conditions, to ensure the analytical accuracy of NGV computational fluid dynamics (CFD) and computational solid dynamics (CSD), respectively.
The remainder of this paper is organized as follows.
Section 2 introduces the modeling and simulation approaches including physical model, material parameters, boundary conditions, meshing, and simulation procedure. The verification strategy involving the turbulence model and temperature test is discussed in
Section 3. In
Section 4 the results and discussions on flow characteristic analysis, temperature field analysis, and thermo-structural analysis are investigated.
Section 5 gives the conclusions and findings of this paper.
4. Result and Discussions
This section will discuss the integrated analysis of film cooling NGV to validate the effectiveness of the developed enhanced FTS model in computing precision from flow characteristics, temperature distributions, and fluid-structural coupling characteristics, respectively.
4.1. Flow Characteristic Analysis
Based on the developed enhanced FTS model, the effects of static pressure and Mach number around the NGV on temperature distribution were studied.
Figure 10 shows static pressure and Mach number distribution on midspan of Case 1.
As shown in
Figure 10a, the peak pressure appears in the stagnation zone of the leading edge. The distributions law of static pressure on midspan is similar to that in
Figure 6, which basically proves the effectiveness of the proposed model. As the pressure wave at suction side is distinct, the rapid expansion of mainstream enhances the Mach number to the maximum (closing to that of the engine entrance) at the second half of the suction side. The increase of gas flow rate greatly increases the heat transfer rate in the region, which is also the basis of the heat transfer characteristic analysis of the NGV surface.
Figure 11 shows the distribution of static pressure differences and Mach number differences between Case 1 under the standard condition and Case 6 under the mean temperature inlet condition at midspan.
As illustrated in
Figure 11, the static pressure increases with the increasing inlet temperature, and influences the flow performances of internal cooling air. As the pressure of mainstream rises, the cooling air cannot flow out of the holes at the trailing edge, and radial velocity enlarges. As the flow rate of cooling air directly effects the distribution of thermal stress around the cooling holes, the calculation results can provide a reference for the location of stress concentration.
In the integrated analysis of NGV, HTC is an important parameter of determining temperature distribution.
Figure 12 shows the flow-heat transfer performance on both the outer and inner surface under the condition of Case 1.
Tsp = 1310 and 491 K were employed to calculate outer and inner HTC, respectively.
As revealed in
Figure 12, four regions are denoted by A, B, C, and D, to study the HTC performance. Large HTCs that appeared on regions A and D are induced by high flow speed and high pressure in
Figure 10. All cooling air injects into NGV through a small hole at the bottom, and causes the local severe heat transfer in region C. The cooling air injected from a small hole directly attacks against region B. In this case, the local HTC on the suction side is improved. In addition, the cooling gas flow outside the outer hub has a circumferential velocity. Therefore, the simulation of HTC is reasonable and effective to validate the effectiveness of CHT calculation.
4.2. Temperature Field Analysis
Figure 13 shows temperature distribution contours of Case 1 and TSP test results for the NGV. As illustrated in
Figure 13, high temperature appears at both the leading edge and trailing edge with the maximum 1205 K at the center of the vane airfoil on the trailing edge (50% height), and the temperature gradually decreases in the chord direction to a local minimum 821 K at film cooling holes, and the temperatures on the vane agree with these of the TSP standard model in respect of TSP-M02, TSP-M05, and TSP-M07, because the maximum calculation error is only 4.1%. The simulation temperatures at the inner and outer hub of the leading edge are 730–962 K and 802–896 K, respectively. For the same position of TSP test, the temperatures in TSP-M04, TSP-S01, and TSP-M10 are 694–966 K and 801–864 K. Obviously, the maximum error is 5.2% indicated in
Figure 13b, which displays that the location and value calculated by the CFD simulation are consistent with the TSP test. In previous works, the NGV was discussed under the same condition using an average temperature inlet and SST model [
16]. The results revealed that the temperature of the outer hub of the leading edge varied in [720 K, 808 K] which is much lower than that of TSP test in [801 K, 964 K], and had the error range [6.4%, 10.1%]. Compared to the maximum error 10.1% in the previous work, therefore, the proposed enhanced FTS model is accurate owing to the maximum error of 5.2%.
On the trailing side, a higher temperature observed by the thermal load was relatively lower due to no internal passage. The maximum temperature difference between cooling holes and the trailing edge was 384 K which was quite large for a hollow structure. Similarly, the maximum temperature 1190 K on the pressure side localized at 2/3 the height of the leading edge on the vane airfoil. The same height had the peak value of inlet temperature profile. Moreover, in the inner passage, the air jet raised the temperature and formed a tongue-shaped temperature contour at the suction side and pressure side. This phenomenon is consistent with that observed in the TSP test and the distribution of HTC.
Figure 14 shows temperature profiles distributions at different heights and the total mass flow of cooling air from A1 to A4. As illustrated in
Figure 14, the direction of cooling air is positive along the outlet direction of holes. Due to the unequal distribution of cooling air mass flow under different suctions, the maximum temperatures are almost same as 25% and 50% spanwise of the leading edge and trailing edge. The temperature curves at the leading edge are smoother than that of the trailing edge, which indicates that the thermal deformation is relatively gentle and increasing the gradient of inlet temperature can enlarge the temperature gradient in the midspan. As the flame peak shifts from the outer to inner hub, the upper temperature decreases obviously. The max-temperature drop on the suction side is 8%. The distribution of temperature profiles regarding the uniform temperature inlet is different from the test results in
Figure 13. Without non-uniform inlet temperature, the midspan temperature at the leading edge is the lowest in all Cases. By contrast, the temperature at 75% height on the trailing edge is the highest. The total mass flow of holes under different lines slightly changes with the increasing inlet temperature gradient.
4.3. Thermo-Structural Analysis
A large enough gap between parts is required due to the thermal expansion under high-temperature operation. As collision and compression always unavoidably appear among different parts of the guide vane rim, a periodic boundary condition was utilized to prevent the circumferential displacement of the NGV as shown in
Figure 3. To find the structure strength of the NGV, the equivalent stress
σvon (also called von Mises stress) was adopted, i.e.,
where
σx,
σy, and
σz indicate the stresses in
x,
y, and
z directions, respectively.
The aperture of NGV connections is large enough (i.e., larger than the deformation caused by thermal expansion) to allow the vane to move freely [
35]. Thus, the thermal stress caused by the connection structure is negligibly small, which means a free boundary may be suitable for this problem. However, according to the thermal-elastic constitutive equations, if all boundaries are free, the equations will lack constraints. In this case, the weak spring approach is used to avoid computational divergence. Weak spring was added at eight grid nodes at the boundaries on three directions, as shown in
Figure 15. The weak springs provide a virtual force on the structure boundaries, so that the convergence can be ensured. To reduce the boundary force, the spring stiffness should be as small as possible. However, when the stiffness coefficient is small enough, the simulation will be diffused. To find the balance between computational convergence and over-constrained, the thermal stress results of four stiffness coefficients K
s are shown in
Figure 16. The increase of spring stiffness will lead to stress concentration at the grid nodes. Obviously, increasing the spring stiffness could not reflect the real situation. According to the simulation test, this paper considers the spring stiffness as 1 N/mm.
With respect to the FE analysis, the expansion and total mesh displacement are shown in
Figure 17. As revealed in
Figure 17, the maximum mesh displacement was 1.72 mm. As it is difficult to observe the deformation in one-to-one scaled images, the deformation in
Figure 17 was displayed by magnifying 65 times. As shown in
Figure 13, the outer and inner hub at the leading edge are cooler than the same positions of the trailing edge. Therefore, the trailing edge mainly bears the tension load. The deformation was proportional to the radial direction.
Guo [
36] studied a type of NGV with a similar structure, material, and working environment. The comparison of the Von Mises stress on the NGV surface with the actual cracks [
36] is shown in
Figure 18. Compared with the experiment, the locations of predicted stress concentration show the consistency with the cracks on the gas turbine vanes after an operating period.
Generally, the thermal stress is induced by the total thermal expansion from hot mainstream in vane cascade and the centralized cooling structures, such as cooling holes, inject holes, etc. As seen in
Figure 18, thermal stress concentrations exist at the junctions between the vane and hub, because vane ring limits radial expansion. The stresses may be relaxed by junction chamber described in
Table 1.
The other thermal stress concentrations occur at the edges of the cooling hole at the trailing edge. The maximum stress (758 MPa) appears in the fifth cooling hole counting from the hub. Specifically, the number of cracks on the holes of the trailing edge are more than that of the leading edge. Thus, the thermal stress concentration in cooling holes is dangerous as to induce cracks when a mass of cooling air goes through a small hole in hot metallic materials.
4.4. Effect of Non-Uniform Temperature Inlet
The aim of integrated analysis is to show how the flow environment affects structural thermal stress.
Figure 19 shows the relationship between cooling air mass flow rate and thermal stress under different cooling holes at the trailing edge from Case 1 to Case 6. Under the standard conditions, the air mass flow first increases and then decreases in the cooling holes in the radial direction. The kinetic energy of cooling gas reaches the maximum between No. 6 and No. 7 holes, and then declines slowly. In most cases, the distribution of maximum stress in holes is similar to the distribution of air mass flow. However, it is more sensitive than the cooling air flow. With the increasing inlet temperature gradient, the maximum hole mass flow moves from hole No. 6 to No. 7, resulting from the increasing radial velocity indicated in
Figure 11b. The results of integrated analysis show that the slight change of aerodynamic environment may lead to a significant increase in the thermal stress of NGV, which is different from the findings in the traditional isolation analysis.
5. Conclusions
The target of this paper was to perform the integrated analysis of film cooling nozzle guide vane (NGV) by proposing an enhanced fluid-thermo-structural model, by adopting an efficient turbulence model (i.e., SST γ-θ model), and weak spring approach, in respect to computational fluid dynamics (CFD) and computational solid dynamics (CSD). Through the validation of the enhanced model and the integrated analysis of film cooling NGV involving the characteristics of flow field, temperature field, and thermo-structural coupling field, some conclusions are summarized as follows:
The enhanced FTS model can precisely predict flow field, temperature field, and thermo-structural coupling field, following the general working state of film cooling NGVs. Compared with the traditional method, the accuracy of temperature field calculation is improved by about 5%.
The simulated results of pressure and convective heat transfer coefficient with SST γ-θ model agree well with test data. Both temperature distribution and crack generation position are basically consistent with a real vane and only have an error of <6% of the maximum predicted temperature. It is indicated that the enhanced FTS model is accurate and effective.
The increasing inlet temperature gradient hardly affects the pressure distribution at the midspan. In this case, however, the radial velocity of the inner cooling gas near the trailing edge holes increase, and temperature gradient and thermal stress is enhanced by about 7.5%. The peak change of gas temperature from the outer to inner hub hardly influences the distribution of cooling air, while the max thermal stress reduces by 16%. It is revealed that thermal stress is largely affected by aerodynamic characteristics and the enhanced FTS model is reasonable and effective.
Thermal stress concentrations are located at the hole edges of the trailing edge near the outer hub and the junction between the vane and ring, respectively. Although the temperature around the holes is small, the thermal stress is almost twice that at junctions. Therefore, the cracks appear at the edge of holes before appearing at the junctions. This is significant for designing film cooling NGV.
In short, the developed enhanced FTS model is validated to hold high-computational precision and efficiency in the integrated analysis of film cooling NGV, by comparing the temperature characteristics, fluid field distribution, and thermo-structural coupling characteristics with the experimental investigation. The efforts of this study provide a promising modeling strategy for the integrated design of NGV in engineering.