Figure 1.
Cross-section of the structure of typical single-core cable.
Figure 1.
Cross-section of the structure of typical single-core cable.
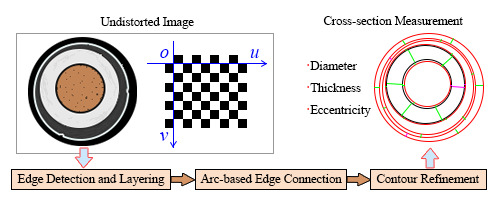
Figure 2.
Flow diagram of the proposed vision-based framework for power cable cross-section measurement.
Figure 2.
Flow diagram of the proposed vision-based framework for power cable cross-section measurement.
Figure 3.
Coordinate systems.
Figure 3.
Coordinate systems.
Figure 4.
Edge filtering based on length and linearity. (a) Long structural edges; (b) Very short interference details; (c) Pending short edges; (d) Short structural edges with fairly good linearity.
Figure 4.
Edge filtering based on length and linearity. (a) Long structural edges; (b) Very short interference details; (c) Pending short edges; (d) Short structural edges with fairly good linearity.
Figure 5.
Arc-based edge connection, in which red dots are clockwise organized edge points to be connected, red asterisks denote arc endpoints, and green line denotes the fitted circular contour . (a) Direct connection with connecting line ; (b) PSC method, in which red arrow shows the tangential direction of at , denotes the prediction point, magenta arrow shows the normal direction of at , and blue boxes indicate the search range for gradient calculation.
Figure 5.
Arc-based edge connection, in which red dots are clockwise organized edge points to be connected, red asterisks denote arc endpoints, and green line denotes the fitted circular contour . (a) Direct connection with connecting line ; (b) PSC method, in which red arrow shows the tangential direction of at , denotes the prediction point, magenta arrow shows the normal direction of at , and blue boxes indicate the search range for gradient calculation.
Figure 6.
Fluctuations in initial contour , in which red dots are contour points, green line denotes the fitted circular contour , and fluctuations exist in blue ellipse. (a) Structure-related gentle changes; (b) Mutations with steep changes.
Figure 6.
Fluctuations in initial contour , in which red dots are contour points, green line denotes the fitted circular contour , and fluctuations exist in blue ellipse. (a) Structure-related gentle changes; (b) Mutations with steep changes.
Figure 7.
Breaks detection and mutation grouping, in which horizontal axis is polar angle , vertical axis is radial distance to the fitted circle, green solid line denotes original sequence, red dashed line denotes the simplified sequence, blue line is the absolute difference of , and the segments divided by break groups are labeled. (a) I-Break in magenta lines with detected major peaks in circles; (b) P-Break in orange lines with a detected major peak in circle.
Figure 7.
Breaks detection and mutation grouping, in which horizontal axis is polar angle , vertical axis is radial distance to the fitted circle, green solid line denotes original sequence, red dashed line denotes the simplified sequence, blue line is the absolute difference of , and the segments divided by break groups are labeled. (a) I-Break in magenta lines with detected major peaks in circles; (b) P-Break in orange lines with a detected major peak in circle.
Figure 8.
Break between point and in polar coordinate system, in which denotes the pole, and denote polar coordinates, is radius of the fitted circle, is radial distance between contour point and the fitted circle, and are radial and angular difference between the two points, and is the angle between line and radial direction at point .
Figure 8.
Break between point and in polar coordinate system, in which denotes the pole, and denote polar coordinates, is radius of the fitted circle, is radial distance between contour point and the fitted circle, and are radial and angular difference between the two points, and is the angle between line and radial direction at point .
Figure 9.
LTBC to of I-Mutation, in which vertical axis is radial distance to the fitted circle, and horizontal axis is the dynamic number rather than polar angle , to avoid the discontinuity of clockwise ranging from to . The blue lines are , red lines are corresponding fitted lines, the magenta and green solid lines are detected I-Mutation, black arrow is the translation for correction, and the magenta and green dashed lines are corrected sequence.
Figure 9.
LTBC to of I-Mutation, in which vertical axis is radial distance to the fitted circle, and horizontal axis is the dynamic number rather than polar angle , to avoid the discontinuity of clockwise ranging from to . The blue lines are , red lines are corresponding fitted lines, the magenta and green solid lines are detected I-Mutation, black arrow is the translation for correction, and the magenta and green dashed lines are corrected sequence.
Figure 10.
Cross-section measurement. (a) Perimeter measurement, in which red dots are contour and blue asterisks are vertexes of convex hull; (b) Thickness measurement, in which magenta line is minimum thickness and green lines are the other five thickness measurements clockwise.
Figure 10.
Cross-section measurement. (a) Perimeter measurement, in which red dots are contour and blue asterisks are vertexes of convex hull; (b) Thickness measurement, in which magenta line is minimum thickness and green lines are the other five thickness measurements clockwise.
Figure 11.
Simulated images. (a) Original image ; (b) Image with additive Gaussian noise and salt and pepper noise.
Figure 11.
Simulated images. (a) Original image ; (b) Image with additive Gaussian noise and salt and pepper noise.
Figure 12.
Edge detection and layering of with mixed noise. (a) Candidate edges by Canny detection; (b) Structural edges by filtering based on length and linearity; (c) Layering result of , in which edges in different layers are rendered with different colors.
Figure 12.
Edge detection and layering of with mixed noise. (a) Candidate edges by Canny detection; (b) Structural edges by filtering based on length and linearity; (c) Layering result of , in which edges in different layers are rendered with different colors.
Figure 13.
Arc-based edge connection, in which yellow dots are previous edges and magenta dots are arc-based connections. (a) Edge connection of ; (b) Edge connection of .
Figure 13.
Arc-based edge connection, in which yellow dots are previous edges and magenta dots are arc-based connections. (a) Edge connection of ; (b) Edge connection of .
Figure 14.
connection and refinement. (a) Arc-based connection of with the enhanced grayscale image as base map, in which yellow dots are , blue dots denote search range and magenta asterisks are accepted search points; (b) Partial enlargement of (a); (c) LTBC to a mutation in edge connection result, in which yellow dots are initial closed and red dots are refined results after corrections to detected mutation.
Figure 14.
connection and refinement. (a) Arc-based connection of with the enhanced grayscale image as base map, in which yellow dots are , blue dots denote search range and magenta asterisks are accepted search points; (b) Partial enlargement of (a); (c) LTBC to a mutation in edge connection result, in which yellow dots are initial closed and red dots are refined results after corrections to detected mutation.
Figure 15.
General view of cross-section measurement. (a) Perimeter and thickness for , in which red dots are extracted contour points, blue asterisks are vertexes of contour convex hull, magenta lines denote minimum thickness , and green lines are the other five thickness measurements clockwise; (b) Perimeter and thickness for .
Figure 15.
General view of cross-section measurement. (a) Perimeter and thickness for , in which red dots are extracted contour points, blue asterisks are vertexes of contour convex hull, magenta lines denote minimum thickness , and green lines are the other five thickness measurements clockwise; (b) Perimeter and thickness for .
Figure 16.
Image of actual specimen cross-section.
Figure 16.
Image of actual specimen cross-section.
Figure 17.
Coarse contour extraction of metal layers. (a) Extracted plotted with red dots on component; (b) Extracted in blue dots and in green dots; (c) Partial enlargement of (b), in which deviations are circled.
Figure 17.
Coarse contour extraction of metal layers. (a) Extracted plotted with red dots on component; (b) Extracted in blue dots and in green dots; (c) Partial enlargement of (b), in which deviations are circled.
Figure 18.
Edge detection. (a) Candidate edges by Canny detection. (b) Structural edges by filtering based on length and linearity features.
Figure 18.
Edge detection. (a) Candidate edges by Canny detection. (b) Structural edges by filtering based on length and linearity features.
Figure 19.
Edge layering. (a) Extraction based on previous coarse contours, in which edges in different layers are rendered with different colors; (b) Annulus division of the left structural edges, in which different annuli are rendered with different colors; (c) Annuli with structural edges.
Figure 19.
Edge layering. (a) Extraction based on previous coarse contours, in which edges in different layers are rendered with different colors; (b) Annulus division of the left structural edges, in which different annuli are rendered with different colors; (c) Annuli with structural edges.
Figure 20.
Layering result of edge points. (a) Layered edges plotted in red dots; (b) Partial enlargement of (a), in which red dots are layered edges, green lines are the fitted circular contour, and interferences and discontinuity exist in blue and magenta ellipses.
Figure 20.
Layering result of edge points. (a) Layered edges plotted in red dots; (b) Partial enlargement of (a), in which red dots are layered edges, green lines are the fitted circular contour, and interferences and discontinuity exist in blue and magenta ellipses.
Figure 21.
Arc-based edge connection result. (a) All connection locations, in which yellow dots are previous result and magenta dots are connections; (b) Closed initial after arc connection.
Figure 21.
Arc-based edge connection result. (a) All connection locations, in which yellow dots are previous result and magenta dots are connections; (b) Closed initial after arc connection.
Figure 22.
connection plotted on enhanced image. (a) connection, in which yellow dots are previous and magenta dots are connections; (b) Partial enlargement of (a) with accurate connections; (c,d) are partial enlargements of (a) with inaccurate in yellow.
Figure 22.
connection plotted on enhanced image. (a) connection, in which yellow dots are previous and magenta dots are connections; (b) Partial enlargement of (a) with accurate connections; (c,d) are partial enlargements of (a) with inaccurate in yellow.
Figure 23.
LTBC to detected mutations, in which yellow dots are initial closed contours and red dots are corrections. (a) LTBC to a detected P-Mutation in ; (b) LTBC to detected P-Mutations in .
Figure 23.
LTBC to detected mutations, in which yellow dots are initial closed contours and red dots are corrections. (a) LTBC to a detected P-Mutation in ; (b) LTBC to detected P-Mutations in .
Figure 24.
General view of cross-section measurement. (a) Perimeter measurement, in which red dots are extracted contour and blue asterisks are vertexes of contour convex hull; (b) Thickness measurement, in which magenta line denotes and green lines are the other five measurements clockwise.
Figure 24.
General view of cross-section measurement. (a) Perimeter measurement, in which red dots are extracted contour and blue asterisks are vertexes of contour convex hull; (b) Thickness measurement, in which magenta line denotes and green lines are the other five measurements clockwise.
Figure 25.
Cutting burrs of outermost contour.
Figure 25.
Cutting burrs of outermost contour.
Figure 26.
Coordinates differences between mapped and actual chessboard world coordinates of chessboard corners. (a) The coordinates differences in two experiments of simulated cable images; (b) The coordinates differences in four experiments of actual cable images.
Figure 26.
Coordinates differences between mapped and actual chessboard world coordinates of chessboard corners. (a) The coordinates differences in two experiments of simulated cable images; (b) The coordinates differences in four experiments of actual cable images.
Table 1.
Diameter measurement results for and . (unit: mm).
Table 1.
Diameter measurement results for and . (unit: mm).
| Layer | | | | | |
|---|
| 8 | 115.470 | 115.958 | 0.488 | 115.772 | 0.302 |
| 7 | 105.600 | 105.694 | 0.094 | 105.499 | 0.101 |
| 6 | 99.910 | 100.557 | 0.647 | 100.390 | 0.480 |
| 5 | 85.330 | 85.791 | 0.461 | 86.292 | 0.962 |
| 1 | 46.752 | 46.901 | 0.149 | 46.681 | 0.071 |
| RMSE | - | - | 0.424 | - | 0.502 |
Table 2.
Thickness measurement results for and . (unit: mm).
Table 2.
Thickness measurement results for and . (unit: mm).
| Layer | Manual | | |
|---|
| | | | | | | | | |
|---|
| 8 | 4.820 | 4.995 | 4.941 | 0.121 | 5.051 | 0.099 | 4.936 | 0.116 | 5.074 | 0.079 |
| 7 | 2.450 | 2.552 | 2.446 | 0.004 | 2.476 | 0.048 | 2.411 | 0.039 | 2.516 | 0.036 |
| 5 | 1.520 | 1.552 | 1.328 | 0.192 | 1.510 | 0.073 | 0.999 | 0.521 | 1.646 | 0.094 |
| 4 | 14.980 | 15.045 | 14.944 | 0.036 | 14.896 | 0.036 | 14.894 | 0.086 | 15.041 | 0.004 |
| 3 | 1.900 | 2.020 | 1.891 | 0.009 | 2.045 | 0.032 | 1.861 | 0.039 | 2.033 | 0.013 |
| RMSE | - | - | - | 0.103 | | 0.063 | | 0.243 | | 0.058 |
Table 3.
Eccentricity measurement of insulation layer in and .
Table 3.
Eccentricity measurement of insulation layer in and .
| Method | | | Insulation Eccentricity |
|---|
| Manual | 15.180 | 14.980 | 0.013 |
| 15.171 | 14.944 | 0.015 |
| 15.106 | 14.894 | 0.014 |
Table 4.
Measurement results of actual specimen cross-section. (unit: mm).
Table 4.
Measurement results of actual specimen cross-section. (unit: mm).
| Layer | | | | | | | | | |
|---|
| 8 | 118.729 | 119.207 | 0.478 | 4.940 | 4.839 | 0.101 | 7.628 | 7.903 | 0.275 |
| 7 | 103.387 | 103.098 | 0.289 | 2.340 | 2.209 | 0.131 | 2.747 | 2.798 | 0.051 |
| 6 | 96.784 | 97.580 | 0.796 | - | - | - | - | - | - |
| 5 | 86.803 | 87.984 | 1.181 | 0.930 | 0.803 | 0.127 | 1.062 | 1.303 | 0.241 |
| 4 | - | - | - | 16.140 | 15.438 | 0.702 | 16.325 | 16.175 | 0.150 |
| 3 | - | - | - | 1.440 | 1.477 | 0.037 | 1.567 | 2.042 | 0.475 |
| 1 | 48.000 | 48.176 | 0.176 | - | - | - | - | - | - |
| RMSE | - | - | 0.689 | - | - | 0.328 | - | - | 0.281 |
Table 5.
Eccentricity measurement of insulation layer.
Table 5.
Eccentricity measurement of insulation layer.
| Method | | | Insulation Eccentricity
|
|---|
| Manual | 16.560 | 16.140 | 0.025 |
| Image | 16.631 | 15.438 | 0.072 |
Table 6.
Measurement errors of diameters and thicknesses in four experiments. (unit: mm).
Table 6.
Measurement errors of diameters and thicknesses in four experiments. (unit: mm).
| Layer | 8 | 7 | 6 | 5 | 4 | 3 | 1 | RMSE | RMSEa |
|---|
| 0.478 | 0.289 | 0.796 | 1.181 | - | - | 0.176 | 0.689 | 0.768 |
| 0.702 | 0.073 | 0.984 | 1.627 | - | - | 0.116 | 0.908 |
| 0.568 | 0.192 | 0.876 | 1.132 | - | - | 0.056 | 0.694 |
| 0.611 | 0.145 | 0.893 | 1.362 | - | - | 0.078 | 0.781 |
| 0.101 | 0.131 | - | 0.127 | 0.702 | 0.037 | - | 0.328 | 0.308 |
| 0.428 | 0.038 | - | 0.113 | 0.343 | 0.070 | - | 0.253 |
| 0.434 | 0.028 | - | 0.110 | 0.518 | 0.170 | - | 0.316 |
| 0.377 | 0.012 | - | 0.090 | 0.614 | 0.204 | - | 0.337 |
| 0.275 | 0.051 | - | 0.241 | 0.183 | 0.475 | - | 0.281 | 0.327 |
| 0.326 | 0.118 | - | 0.413 | 0.219 | 0.475 | - | 0.336 |
| 0.304 | 0.144 | - | 0.360 | 0.190 | 0.394 | - | 0.295 |
| 0.289 | 0.144 | - | 0.607 | 0.245 | 0.507 | - | 0.397 |
Table 7.
Measurement errors of insulation eccentricity in four experiments.
Table 7.
Measurement errors of insulation eccentricity in four experiments.
| Experiment | | | Insulation Eccentricity
| Error | Errora |
|---|
| 1 | 16.631 | 15.438 | 0.072 | 0.047 | 0.026 |
| 2 | 16.429 | 15.797 | 0.038 | 0.013 |
| 3 | 16.417 | 15.622 | 0.048 | 0.023 |
| 4 | 16.289 | 15.526 | 0.047 | 0.022 |