A Discussion on the Effective Ventilation Distance in Dead-End Tunnels
Abstract
:1. Introduction
2. Materials and Methods
2.1. Geometries
2.2. Discretization
2.3. CFDs Model
2.4. Turbulence Model
2.5. Boundary Conditions
2.6. Software Configuration
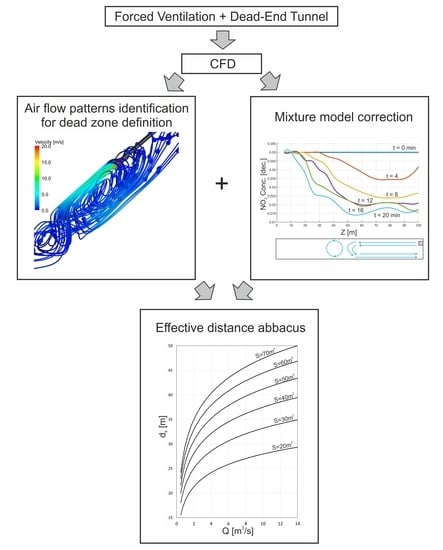
2.7. Dead Zone Delimitation
2.8. Mixture Model
3. Results and Discussion
3.1. Dead Zone Delimitation and Flow Field Patterns
3.2. Mathematical Model for the Effective Distance
- ez: effective distance (m);
- Dh: hydraulic diameter of the tunnel section (m);
- Q: ventilation flow rate (m/s);
- ρ: air density (kg/m3);
- μ: air dynamic viscosity (Pa·s).
- A: cross-sectional area of the tunnel (m2);
- Pw: perimeter of the cross-section (m).
3.3. Mathematical Model Correction with the Mixture Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| C1ε | Constant (-) (value 1.44) |
| C2ε | Constant (-) (value 1.92) |
| C3ε | Constant (-) |
| Cμ | Constant (-) (value 0.09) |
| F | Model-dependent source terms (Pa m−1) |
| Gb | Generation of k due to buoyancy (m2 s−2) |
| Gk | Generation of k due to mean velocity gradients (m2 s−2) |
| I | Identity matrix (-) |
| k | Turbulent kinetic energy (m2 s−2) |
| P | Pressure (Pa) |
| S | Tunnel section (m2) |
| Sk | User-defined source terms for k (m2 s−2) |
| Sm | Sources of mass (kg m−3 s−1) |
| Sε | User-defined source terms for ε (m2 s−2) |
| t | Time (s) |
| u | velocity in x axis (m s−1) |
| v | velocity in y axis (m s−1) |
| va | Absolute velocity (m s−1) |
| w | velocity in z axis (m s−1) |
| YM | Contribution of the fluctuating dilatation in compressible turbulence (m2 s−2) |
| Greek symbols | |
| Stress tensor (Pa) | |
| ε | Dissipation rate (m2 s−3) |
| μ | Dynamic viscosity (Pa s) |
| μt | Tubulent viscosity (Pa s) |
| ρ | Density (kg m−3) |
| σk | Prandtl number for k (-) (value 1.0) |
| σε | Prandtl number for ε (-) (value 1.3) |
References
- Sarmah, M.; Khare, P.; Baruah, B.P. Gaseous emissions during the coal mining activity and neutralizing capacity of ammonium. Water Air Soil Pollut. 2012, 223, 4795–4800. [Google Scholar] [CrossRef]
- Osunmakinde, I.O. Towards safety from toxic gases in underground mines using wireless sensor networks and ambient intelligence. Int. J. Distrib. Sens. Netw. 2013, 2013, 159273. [Google Scholar] [CrossRef]
- Vutukuri, V.S.; Lama, R.D. Environmental Engineering in Mines; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Borísov, S.; Klókov, M.; Gornovói, B. Labores Mineras; Mir: Moscú, Russia, 1976. [Google Scholar]
- Novitzky, A. Ventilación de Minas; L’autor: Buenos Aires, Argentina, 1962. [Google Scholar]
- Kissell, F. Handbook for Methane Control in Mining; DHHS (NIOSH): Pittsburg, PA, USA, 2006; Volume 131.
- Lu, Y.; Akhtar, S.; Sasmito, A.P.; Kurnia, J.C. International Journal of Mining Science and Technology Prediction of air flow, methane, and coal dust dispersion in a room and pillar mining face. Int. J. Min. Sci. Technol. 2017, 27, 657–662. [Google Scholar]
- Ren, T.; Wang, Z.; Cooper, G. CFD modelling of ventilation and dust flow behaviour above an underground bin and the design of an innovative dust mitigation system. Tunn. Undergr. Space Technol. 2014, 41, 241–254. [Google Scholar] [CrossRef]
- Cheng, J.; Li, S.; Zhang, F.; Zhao, C.; Yang, S.; Ghosh, A. CFD modelling of ventilation optimization for improving mine safety in longwall working faces. J. Loss Prev. Process Ind. 2016, 40, 285–297. [Google Scholar] [CrossRef] [Green Version]
- Lolon, S.A.; Brune, J.F.; Bogin, G.E.; Grubb, J.W.; Saki, S.A.; Juganda, A. Computational fluid dynamics simulation on the longwall gob breathing. Int. J. Min. Sci. Technol. 2017, 27, 185–189. [Google Scholar] [CrossRef]
- Sasmito, A.P.; Kurnia, J.C.; Birgersson, E.; Mujumdar, A.S. Computational evaluation of thermal management strategies in an underground mine. Appl. Therm. Eng. 2014, 90, 1144–1150. [Google Scholar] [CrossRef]
- Yuan, L.; Smith, A.C. Computational Fluid Dynamics Modeling of Spontaneous Heating in Longwall Gob Areas; CDC Stacks; Publick Health Publications: Atlanta, GA, USA, 2002.
- Shi, G.Q.; Liu, M.; Wang, Y.M.; Wang, W.Z.; Wang, D.M. Computational Fluid Dynamics Simulation of Oxygen Seepage in Coal Mine Goaf with Gas Drainage. Math. Probl. Eng. 2015, 2015, 723764. [Google Scholar] [CrossRef]
- Diego, I.; Torno, S.; Toraño, J.; Menéndez, M.; Gent, M. A practical use of CFD for ventilation of underground works. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2011, 26, 189–200. [Google Scholar] [CrossRef]
- Toraño, J.; Torno, S.; Menéndez, M.; Gent, M. Auxiliary ventilation in mining roadways driven with roadheaders: Validated CFD modelling of dust behaviour. Tunn. Undergr. Space Technol. 2011, 26, 201–210. [Google Scholar] [CrossRef]
- Sasmito, A.P.; Birgersson, E.; Ly, H.C.; Mujumdar, A.S. Some approaches to improve ventilation system in underground coal mines environment—A computational fluid dynamic study. Tunn. Undergr. Space Technol. 2013, 34, 82–95. [Google Scholar] [CrossRef]
- Toraño, J.; Torno, S.; Menendez, M.; Gent, M.; Velasco, J. Models of methane behaviour in auxiliary ventilation of underground coal mining. Int. J. Coal Geol. 2009, 80, 35–43. [Google Scholar] [CrossRef]
- Li, M.; Aminossadati, S.M.; Wu, C. Numerical simulation of air ventilation in super-large underground developments. Tunn. Undergr. Space Technol. 2016, 52, 38–43. [Google Scholar] [CrossRef]
- Fang, Y.; Yao, Z.; Lei, S. Air flow and gas dispersion in the forced ventilation of a road tunnel during construction. Undergr. Space 2018, 4, 168–179. [Google Scholar] [CrossRef]
- Szlazak, N.; Szlazak, J.; Tor, A.; Obracaj, A.; Borowski, M. Ventilation systems in dead end headings with coal dust and methane hazard. In Proceedings of the 30th Internetional Conferences of safety in Mines Research Institutes, Johannesburg, South Africa, 5–9 October 2003. [Google Scholar]
- Reed, W.; Taylor, C. Factors affecting the development of mine face ventilation systems in the 20th century. In Proceedings of the Society for Mining, Metallurgy and Exploration (SME): Annual Meeting and Exhibit, Denver, CO, USA, 25–28 February 2007. [Google Scholar]
- De La Vergne, J.; Mcintosh, S. Hard Rock Miners Handbook; Stantec: Edmonton, AB, Canada, 2000; Volume 4, ISBN 0-9687006-0-8. [Google Scholar]
- ANSYS. ANSYS FLUENT 16.2 User’s Guide; ANSYS: Canonsburg, PA, USA, 2016. [Google Scholar]
- López González, M.; Galdo Vega, M.; Fernández Oro, J.M.; Blanco Marigorta, E. Numerical modeling of the piston effect in longitudinal ventilation systems for subway tunnels. Tunn. Undergr. Space Technol. 2014, 40, 22–37. [Google Scholar] [CrossRef]
- Ministry of Water Resources of the People’s Republic of China. Construction Specifications on Underground Excavation Engineering of Hydraulic Structures; China Water Power Press: Beijing, China, 2007. [Google Scholar]
- Kurnia, J.C.; Sasmito, A.P.; Mujumdar, A.S. Simulation of a novel intermittent ventilation system for underground mines. Tunn. Undergr. Space Technol. 2014, 42, 206–215. [Google Scholar] [CrossRef]
- Betta, V.; Cascetta, F.; Musto, M.; Rotondo, G. Numerical study of the optimization of the pitch angle of an alternative jet fan in a longitudinal tunnel ventilation system. Tunn. Undergr. Space Technol. 2009, 24, 164–172. [Google Scholar] [CrossRef]
- Ji, J.; Fan, C.G.; Gao, Z.H.; Sun, J.H. Effects of Vertical Shaft Geometry on Natural Ventilation in Urban Road Tunnel Fires. J. Civ. Eng. Manag. 2014, 20, 466–476. [Google Scholar] [CrossRef]
- Feroze, T.; Genc, B. Analysis of the effect of ducted fan system variables on ventilation in an empty heading using CFD. J. S. Afr. Inst. Min. Metall. 2017, 117, 157–167. [Google Scholar] [CrossRef] [Green Version]















| Geometrical Parameters for Each Scenario | Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| A | H | R | Rd | D | Ld | Lt | S | ||
| Units | m | m2 | |||||||
| Scenario | 1 | 5.4 | 1.8 | 2.7 | 1.8 | 0.54 | 50 | 100 | 21.17 |
| 2 | 6 | 2 | 3 | 2 | 0.60 | 26.13 | |||
| 3 | 7.2 | 2.4 | 3.6 | 2.4 | 0.72 | 37.63 | |||
| 4 | 9 | 3 | 4.5 | 3 | 0.90 | 58.80 | |||
| Turbulence Model | Realizable k-ε with Non-Equilibrium |
|---|---|
| Pressure–Velocity Coupling | SIMPLE Scheme |
| Transient Formulation | Second-Order Implicit |
| Spatial Discretization | |
| Gradient | Green-Gauss Cell-Based |
| Pressure | Second Order |
| Momentum | Second Order |
| Turbulent Kinetic Energy | Second Order |
| Turbulent Dissipation Rate | Second Order |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Díaz, M.; Sierra, C.; Miguel-González, C.; Pereiras, B. A Discussion on the Effective Ventilation Distance in Dead-End Tunnels. Energies 2019, 12, 3352. https://doi.org/10.3390/en12173352
García-Díaz M, Sierra C, Miguel-González C, Pereiras B. A Discussion on the Effective Ventilation Distance in Dead-End Tunnels. Energies. 2019; 12(17):3352. https://doi.org/10.3390/en12173352
Chicago/Turabian StyleGarcía-Díaz, Manuel, Carlos Sierra, Celia Miguel-González, and Bruno Pereiras. 2019. "A Discussion on the Effective Ventilation Distance in Dead-End Tunnels" Energies 12, no. 17: 3352. https://doi.org/10.3390/en12173352
APA StyleGarcía-Díaz, M., Sierra, C., Miguel-González, C., & Pereiras, B. (2019). A Discussion on the Effective Ventilation Distance in Dead-End Tunnels. Energies, 12(17), 3352. https://doi.org/10.3390/en12173352