Regulation Performance of Multiple DC Electric Springs Controlled by Distributed Cooperative System
Abstract
:1. Introduction
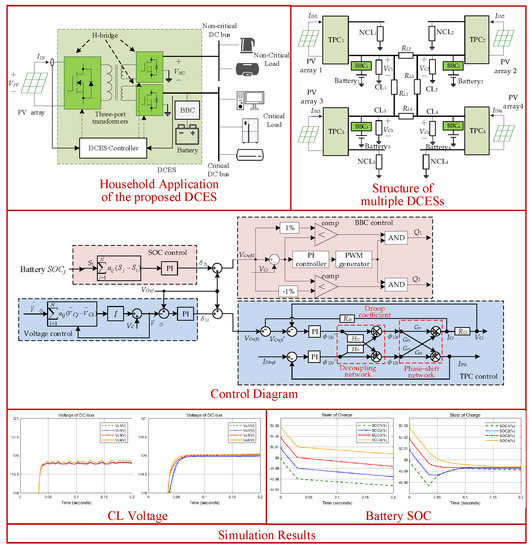
2. DCES Topology and Operation
3. Distributed Cooperative Control
3.1. Primary Control
3.2. Secondary Control
4. Steady State Analysis
4.1. Consensus of the CL Average Voltage
4.2. Consensus of the Battery SOC
5. Simulation Results
5.1. Steady State
5.2. Converter Failure
5.3. Communication Weight Variation
5.4. Load Variation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hui, S.Y.; Lee, C.K.; Wu, F.F. Electric springs—A new smart grid technology. IEEE Trans. Smart Grid 2012, 3, 1552–1561. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, M.; Jiang, Y.; Zuo, W.; Buja, G. A Simple Active and Reactive Power Control for Applications of Single-Phase Electric Springs. IEEE Trans. Ind. Electron. 2018, 65, 6291–6300. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, M.; Chen, Z. Steady-state analysis of electric springs with a novel δ control. IEEE Trans. Power Electron. 2015, 30, 7159–7169. [Google Scholar] [CrossRef]
- Mok, K.; Wang, M.; Tan, S.; Hui, S.Y.R. DC electric springs—A technology for stabilizing DC power distribution systems. IEEE Trans. Power Electron. 2017, 32, 1088–1105. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, M.; Jiang, Y.; Chen, Z.; Deng, F.; Wang, Z. DC electric springs with DC/DC converters. In Proceedings of the IEEE International Power Electronics and Motion Control Conference, Hefei, China, 28 September 2016; pp. 3268–3273. [Google Scholar]
- Wang, M.; Yang, T.; Tan, S.; Hui, S.Y. Hybrid Electric Springs for Grid-Tied Power Control and Storage Reduction in AC Microgrids. IEEE Trans. Power Electron. 2019, 34, 3214–3225. [Google Scholar] [CrossRef]
- Kakigano, H.; Miura, Y.; Ise, T. Distribution Voltage Control for DC Microgrids Using Fuzzy Control and Gain-Scheduling Technique. IEEE Trans. Power Electron. 2013, 28, 2246–2258. [Google Scholar] [CrossRef]
- Ahmadi, R.; Ferdowsi, M. Improving the Performance of a Line Regulating Converter in a Converter-Dominated DC Microgrid System. IEEE Trans. Smart Grid 2014, 5, 2553–2563. [Google Scholar] [CrossRef]
- Huang, P.; Liu, P.; Xiao, W.; El Moursi, M.S. A Novel Droop-Based Average Voltage Sharing Control Strategy for DC Microgrids. IEEE Trans. Smart Grid 2015, 6, 1096–1106. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Miranian, A.; Luna, A.; Rodriguez, P. DC Voltage Control and Power Sharing in Multiterminal DC Grids Based on Optimal DC Power Flow and Voltage-Droop Strategy. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 1171–1180. [Google Scholar] [CrossRef]
- Mok, K.; Wang, M.; Tan, S.; Hui, S. DC electric springs—An emerging technology for DC grids. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Charlotte, NC, USA, 15–19 March 2015; pp. 684–690. [Google Scholar]
- Wang, Q.; Zha, D.; Deng, F.; Cheng, M.; Buja, G. A topology of DC electric springs for DC household applications. IET Power Electron. 2019, 12, 1241–1248. [Google Scholar] [CrossRef]
- Phattanasak, M.; Gavagsaz-Ghoachani, R.; Martin, J.; Nahid-Mobarakeh, B.; Pierfederici, S.; Davat, B. Control of a hybrid energy source comprising a fuel cell and two storage devices using isolated three-port bidirectional DC–DC converters. IEEE Trans. Ind. Appl. 2015, 51, 491–497. [Google Scholar] [CrossRef]
- Bahrami, H.; Farhangi, S.; Iman-Eini, H.; Adib, E. A new interleaved coupled-inductor nonisolated soft-switching bidirectional DC/DC converter with high voltage gain ratio. IEEE Trans. Ind. Electron. 2018, 65, 5529–5538. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, W.; Hug, G.; Kar, S.; Li, Z. Cooperative control of distributed energy storage systems in a microgrid. IEEE Trans. Smart Grid 2015, 6, 238–248. [Google Scholar] [CrossRef]
- Mokhtari, G.; Nourbakhsh, G.; Ghosh, A. Smart coordination of energy storage units (ESUs) for voltage and loading management in distribution networks. IEEE Trans. Power Syst. 2013, 28, 4812–4820. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, M.; Ou, J. A distributed cooperative control strategy based on consensus algorithm in DC microgrid. In Proceedings of the IEEE Conference on Industrial Electronics and Applications, Wuhan, China, 31 May–2 June 2018; pp. 243–248. [Google Scholar]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE USA 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Golsorkhi, M.S.; Shafiee, Q.; Lu, D.D.; Guerrero, J.M. A distributed control framework for integrated photovoltaic-battery-based islanded microgrids. IEEE Trans. Smart Grid 2017, 8, 2837–2848. [Google Scholar] [CrossRef]
- Chen, X.; Shi, M.; Sun, H.; Li, Y.; He, H. Distributed cooperative control and stability analysis of multiple DC electric springs in a dc microgrid. IEEE Trans. Ind. Electron. 2018, 65, 5611–5622. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, H.; Qin, X.; Xing, Y. PWM plus secondary-side phase-shift controlled soft-switching full-bridge three-port converter for renewable power systems. IEEE Trans. Ind. Electron. 2015, 62, 7061–7072. [Google Scholar] [CrossRef]
- Samir, H.; Subhashish, B.; Chandan, C. A novel control principle for a high frequency transformer based multiport converter for integration of renewable energy sources. In Proceedings of the IEEE Industrial Electronics Society. Annual. Conference, Vienna, Austria, 10–13 November 2013; pp. 7984–7989. [Google Scholar]
- Wang, W.; Wang, P.; Ma, T.; Liu, H.; Wu, H. A simple decoupling control method for isolated three-port bidirectional converter in low-voltage DC microgrids. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 20–24 September 2015; pp. 3192–3196. [Google Scholar]
- Nasirian, V.; Davoudi, A.; Lewis, F.L.; Guerrero, J.M. Distributed adaptive droop control for dc distribution systems. IEEE Trans. Energy Convers. 2014, 29, 944–956. [Google Scholar] [CrossRef]
- Kim, S.Y.; Song, H.; Nam, K. Idling port isolation control of three-port bidirectional converter for EVs. IEEE Trans. Power Electron. 2012, 27, 2495–2506. [Google Scholar] [CrossRef]
- Nasirian, V.; Moayedi, S.; Davoudi, A.; Lewis, F.L. Distributed cooperative control of DC microgrids. IEEE Trans. Power Electron. 2015, 30, 2288–2303. [Google Scholar] [CrossRef]
- Chen, X.; Shi, M.; Zhou, J.; Chen, Y.; Zuo, W.; Wen, J.; He, H. Distributed cooperative control of multiple hybrid energy storage systems in a DC microgrid using consensus protocol. IEEE Trans. Ind. Electron. 2019, 1. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]














| Parameter | Values | |
|---|---|---|
| Input Voltage (VIN) | 50 V | |
| Global voltage reference of CL (VCref) | 120 V | |
| Communication weights (aij) | 1 | |
| Resistance of the CL (RC) | RC1, RC3 | 120 Ω |
| RC2, RC4 | 150 Ω | |
| Resistance of the NCL (RNC) | RNC1, RNC2 | 40 Ω |
| RNC3, RNC4 | 60 Ω | |
| Initial droop coefficient (Rd0) | Rd0 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zha, D.; Wang, Q.; Cheng, M.; Deng, F.; Buja, G. Regulation Performance of Multiple DC Electric Springs Controlled by Distributed Cooperative System. Energies 2019, 12, 3422. https://doi.org/10.3390/en12183422
Zha D, Wang Q, Cheng M, Deng F, Buja G. Regulation Performance of Multiple DC Electric Springs Controlled by Distributed Cooperative System. Energies. 2019; 12(18):3422. https://doi.org/10.3390/en12183422
Chicago/Turabian StyleZha, Daojun, Qingsong Wang, Ming Cheng, Fujin Deng, and Giuseppe Buja. 2019. "Regulation Performance of Multiple DC Electric Springs Controlled by Distributed Cooperative System" Energies 12, no. 18: 3422. https://doi.org/10.3390/en12183422
APA StyleZha, D., Wang, Q., Cheng, M., Deng, F., & Buja, G. (2019). Regulation Performance of Multiple DC Electric Springs Controlled by Distributed Cooperative System. Energies, 12(18), 3422. https://doi.org/10.3390/en12183422