Comparison of Physics-Based, Semi-Empirical and Neural Network-Based Models for Model-Based Combustion Control in a 3.0 L Diesel Engine
Abstract
:1. Introduction
- Baseline physics-based model: this model was previously presented by the authors in [12] for control-oriented applications. However, in the present study, the model calibration procedure has been refined and the performance of the model has been improved with respect to the previously reported version. In this approach, the tuning parameters are modeled by means of power-law functions, in which the input parameters are the main engine operating variables.
- ANN physics-based model: this is a new modeling approach, which is based on the use of ANNs to predict the tuning parameters of the aforementioned physics-based model.
- Direct semi-empirical model: in this approach, semi-empirical correlations, which are constituted by power-law functions, are used to directly estimate MFB50, PFP, and BMEP.
- Direct ANN model: this approach exploits feed-forward artificial neural networks to directly estimate MFB50, PFP, and BMEP. Details of the methodology used for the training and optimal selection of the number of neurons are also provided in this study.
- A comparison of the performance of the physics-based model tuned using the methodology introduced in this paper (based on Pearson correlation and partial correlation analysis) with that of the previous version reported in [12].
- A comparison of the accuracy of the four investigated models under steady-state conditions and in transient operation over a WHTC.
- A comparison of the performance of the four investigated models, in terms of required computational time, when they are run on an ETAS ES910 (ETAS, Stuttgart, Germany) rapid prototyping device.
2. Experimental Setup and Engine Conditions
- a complete engine map (123 tests, indicated with the blue circles in Figure 2).
- EGR-sweep tests (162 tests, carried out on the points indicated with the red diamonds in Figure 2).
- sweep tests of the main injection timing (SOImain) and injection pressure (pf) (125 tests, carried out on the points indicated with the black circles in Figure 2).
3. Description of the Models
3.1. Physics-Based Model
- A new procedure for the identification of the optimal set of input parameters is developed. This procedure is based on the joint use of the Pearson correlation analysis, partial correlation analysis, and sensitivity analysis, and it allows the performance of the baseline physics-based model to be improved with respect to the previously developed versions.
- An alternative mathematical method (i.e., ANNs) is used to estimate the model calibration parameters:where x0, x1,…, xn are correlation variables. This approach has never been investigated before, and is denoted as “ANN physics-based model”.
3.2. Direct Semi-Empirical Models
3.3. Direct Artificial Neural Networks
4. Selection of the Model Input Variables
- The power-law correlations or the ANNs that evaluate the calibration parameters of the baseline physics-based model and of the ANN physics-based model, respectively.
- The direct semi-empirical model that estimates MFB50, PFP, BMEP.
- The direct ANN model that estimates MFB50, PFP, BMEP.
- First, the Pearson correlation coefficient is calculated for all the possible combinations of the 46 variables reported in Table 3 (the results are reported in Appendix A in Table A1). This coefficient measures the linear dependence between two variables, xi and xj, and is defined as follows:where cov(xi, xj) is the covariance between xi and xj, while var(xi) and var(xj) are the variances of xi and xj, respectively. The Pearson correlation coefficient varies between −1 and +1.After the analysis of the Pearson correlation coefficients, an initial candidate set of input variables is identified for each output quantity that has to be estimated (see Table A2 in Appendix A).
- In the second step, the partial correlation coefficient is evaluated between the dependent variables and each input variable of the initial candidate set, when removing the effect of the remaining input variables of the same set. It should be recalled that the partial correlation coefficient is able to measure the linear dependence between two variables, xi and xj, when the effect of the other input variables variable (z1, z2,…, zi) is removed:The partial correlation coefficient is more robust than the Pearson coefficient. However, the number of parameters should not be too high, otherwise, the consistency of the method decreases. Also, the partial correlation coefficient varies between −1 and +1. As reported in Appendix A (see Table A3), the simultaneous analysis of the Pearson and of the partial correlation coefficients has allowed the least and most robust correlation variables of the initial candidate set to be identified for each dependent output variable. Therefore, some variables were excluded from the initial candidate set identified in step 1 (since they showed low values of the Pearson and partial correlation coefficients), while other variables were kept since they showed high values of both the Pearson and partial correlation coefficients.
- The remaining correlation variables of the initial candidate set which showed intermediate values of the Pearson and partial correlation coefficients were analyzed on the basis of a sensitivity analysis, in order to identify those that had to be kept and those that had to be excluded. A power law function, such as that reported in Equation (21), was used to model each output dependent parameter, and all the possible combinations of input variables were identified by evaluating, for each combination, the related model fitting precision, which was quantified by a correlation coefficient Radj:where nexp is the total number of experimental data and k is the total number of free coefficients. The adjusted correlation coefficient Radj takes into account the number of available experimental tests used for the model fitting, in relation to the number of free parameters of the model. In the end, the combinations which led to the best trade-off between the prediction accuracy and the number of input parameters were selected. Details on the sensitivity analysis have not been reported in this paper for the sake of brevity.
5. Results and Discussion
5.1. Improvement to the Baseline Physics-Based Combustion Model
5.2. Direct Semi-Empirical Models of MFB50, PFP, and BMEP
5.3. ANN-Based Models
- With reference to the physics-based model, the power law-based correlations of the calibration parameters were replaced by the corresponding ANNs, and the performance of the resulting model (i.e., the “ANN physics-based model”) was evaluated. Table 8 shows a comparison between the accuracy of the ANN-based correlations and of the power-law based ones in the estimation of the parameters of the physics-based model. It can be observed that all the precisions based on ANNs are higher than those based on the power law correlations. ANNs have in fact been proved to have a powerful ability to catch the non-linear characteristics between input and output parameters
- The performance of the ANNs that were used to directly simulate MFB50, PFP, and BMEP was evaluated
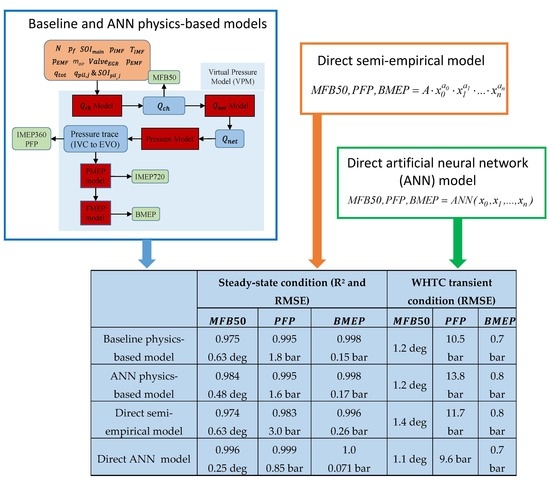
5.4. Comparison of the Four Different Models under Steady-State and Transient Conditions
- it is much simpler in structure and theory and easier to build than the physics-based model;
- it does not require any detailed knowledge or modeling of the physical and chemical processes;
- it is robust not only under steady-state conditions, but also for transient operation;
- its accuracy is high even when a not so large dataset of experimental tests (410) is used for training;
- it features the best accuracy under steady-state and transient operating conditions;
- the required computational time is less than that of the physics-based model (see the next section).
5.5. Analysis of the Computational Time
6. Conclusions
- (1)
- The new methodology set up for the identification of the model input parameters has allowed an improvement to be obtained in the calibration of the baseline physics-based model. Although the accuracy in the estimation of BMEP is quite similar, an improvement in the estimation of PFP, and MFB50 can be obtained, since the related RMSE values decrease from 2.47 bar to 1.82 bar and from 0.86 deg to 0.63 deg, respectively, at steady-state conditions. Moreover, it allows a saving in the model calibration computational time to be achieved.
- (2)
- The direct ANN model has shown the best accuracy in the estimation of MFB50, PFP, and BMEP under both steady-state conditions (RMSE = 0.25 deg, 0.85 bar and 0.071 bar, respectively) and transient operation over the WHTC (RMSE = 1.1 deg, 9.6 bar and 0.7 bar, respectively); the accuracy of the baseline physics-based model is slightly worse than that of the direct ANN model (RMSE = 0.63 deg, 1.8 bar, 0.15 bar under steady-state conditions, RMSE = 1.2 deg, 10.5 bar, 0.8 bar over WHTC).
- (3)
- The accuracy of the ANN physics-based model is higher than that of the baseline physics-based model under steady-state operations (RMSE = 0.48 deg, 1.6 bar, 0.17 bar), but it shows a marked deterioration for transient operation (RMSE = 1.2 deg, 13.8 bar, 0.8 bar), and this approach, therefore, seems to lack robustness.
- (4)
- The accuracy of the semi-empirical model is worse than that of the physics-based model and of the direct ANN model under steady-state conditions (RMSE = 0.63 deg, 3 bar, 0.26 bar) and over the WHTC (RMSE = 1.4 deg, 11.7 bar, 0.8 bar). However, the accuracy can still be considered acceptable, in view of the simple mathematical structure of this kind of model, and the low number of tuning parameters that are necessary (and therefore of experimental data needed for calibration).
- (5)
- The computational time required for the direct ANN model and semi-empirical model is less than 50 μs on an ETAS ES910 rapid prototyping device, while that of the baseline physics-based model is of the order of 350 μs.
- it is much simpler in structure and theory and easier to build than the physics-based model;
- it does not require any detailed knowledge or modeling of the physical and chemical processes;
- it is robust not only under steady-state conditions, but also in transient operation;
- its accuracy is high, even when a not so large dataset of experimental tests (410) is used for training;
- it features the best accuracy under steady-state and transient operating conditions
- the required computational time is lower than that of the physics-based model.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ABDC | After Bottom Dead Center |
| AFst | stoichiometric air-to-fuel ratio |
| ANN | artificial neural network |
| BMEP | Brake Mean Effective Pressure (bar) |
| CFD | Computer Fluid-Dynamics |
| DoE | Design of Experiment |
| ECU | Engine Control Unit |
| EGR | Exhaust Gas Recirculation |
| EOC | End of Combustion |
| EOI | End of Injection |
| EVO | Exhaust Valve Opening |
| FMEP | Friction Mean Effective Pressure (bar) |
| HL | lower heating value of the fuel |
| HCCI | Homogeneous Charge Compression Ignition |
| ICE | Internal Combustion Engines |
| IMEP360 | gross Indicated Mean Effective Pressure (bar) |
| IMEP720 | net Indicated Mean Effective Pressure (bar) |
| IVC | Intake Valve Closing |
| K | combustion rate coefficient |
| m | mass |
| mair | trapped air mass |
| mEGR | trapped EGR mass |
| mf,inj | injected fuel mass (mg per cycle/cylinder) |
| fuel injection rate | |
| MFB50 | crank angle at which 50% of the fuel mass fraction has burned (deg) |
| n | polytropic coefficient for the compression phase |
| n’ | polytropic coefficient for the expansion phase |
| N | engine rotational speed (1/min) |
| O2 | intake charge oxygen concentration (%) |
| p | pressure (bar) |
| PCCI | Premixed Charge Compression Ignition |
| pEMF | exhaust manifold pressure (bar abs) |
| pf | injection pressure (bar) |
| PFP | peak firing pressure |
| pIMF | intake manifold pressure (bar abs) |
| PMEP | Pumping Mean Effective Pressure (bar) |
| q | injected fuel volume quantity (mm3) |
| Qch | chemical heat release |
| Qf,evap | fuel evaporation heat |
| qmain | total injected fuel volume quantity of the main pulse per cycle/cylinder |
| qtot | total injected fuel volume quantity per cycle/cylinder |
| qtot,pil | total injected fuel volume quantity of the pilot pulses per cycle/cylinder |
| Qfuel | chemical energy associated with the injected fuel |
| Qht,glob | global heat transfer of the charge with the walls |
| Qnet | net heat release |
| R2 | squared correlation coefficient |
| RAF | relative air-to-fuel ratio |
| RMS | root mean square |
| RMSE | root mean square error |
| SOC | start of combustion |
| SOI | electric start of injection |
| SVP | support vector machine |
| t | time |
| T | temperature (K) |
| TEMF | exhaust manifold temperature |
| TIMF | intake manifold temperature |
| TSOC | charge temperature at start of combustion |
| TSOI | charge temperature at start of injection |
| V | volume |
| V2X | Vehicle-to-Everything |
| ValveEGR | opening position of the high pressure EGR valve |
| VGT | Variable Geometry Turbine |
| WHTC | Worldwide Harmonized Heavy-duty Transient Cycle |
| Xr,EGR | EGR rate |
Greek Symbols
| Δpexh-int | difference between the exhaust and intake manifold pressure |
| γ | isentropic coefficient |
| ρ | density |
| ρIMF | density in the inlet manifold |
| ρSOC | charge density at the start of combustion |
| ρSOI | charge density at the start of injection |
| τ | ignition delay coefficient |
Appendix A. Correlation Analysis for the Selection of the Model Input Variables
| Variable Name | IN | Variable Name | IN | Variable Name | IN | Variable Name | IN |
|---|---|---|---|---|---|---|---|
| 1 | 13 | 25 | 37 | ||||
| 2 | 14 | 26 | 38 | ||||
| 3 | 15 | 27 | 39 | ||||
| 4 | 16 | 28 | 40 | ||||
| 5 | ρIMF | 17 | 29 | PFP | 41 | ||
| 6 | 18 | 30 | IMEP360 | 42 | |||
| 7 | 19 | 31 | PMEP | 43 | |||
| 8 | 20 | 32 | FMEP | 44 | |||
| 9 | 21 | 33 | IMEP720 | 45 | |||
| pEMF | 10 | 22 | MFB50 | 34 | BMEP | 46 | |
| TEMF | 11 | 23 | 35 | ||||
| 12 | 24 | 36 |

- the input parameters of the correlations which are used to estimate the calibration parameters of the physics-based models (i.e., those reported in Table 3), or the input parameters of the ANNs that are used to estimate the same calibration parameters;
- the input parameters of the semi-empirical correlations that are used to directly estimate MFB50, PFP, BMEP;
- the input parameters of the ANNs that are used to directly estimate MFB50, PFP, BMEP.

- the temporal sequences of the variables in the model have to be taken into account, i.e., variables cannot be used as the independent variables if they are calculated or occur after the dependent variable, according to the scheme in Figure A1;
- the directly measured engine operation variables (namely N, pf, SOI, fuel injection quantity, pIMF, TIMF, ValveEGR) should be considered as independent variable candidates with top priority, because they are the primary cause of the changes in engine operation. Moreover, these variables are usually very precise because they are measured directly in real-time. The generated parameters (ρSOI, TSOI), based on SOI, should be considered with higher priority than those based on SOC (ρSOC, TSOC), because of the uncertainty chain for the estimation of SOC on the basis of SOI;
- the dependent variables (such as τpil, τmain, SOC, Kpil, K1,main, K2,main, Qf,evap, Qht,glob, n, n’, ΔpIMF, PMEP, FMEP) should be considered with a lower priority as correlation parameters, because they are usually less precise than the directly measured parameters. The Xr,EGR, RAF, O2, ρSOC and TSOC generated parameters should also be considered with a lower priority because of their relatively low precision;
- some variable groups (e.g., [SOIpil, SOImain] [qmain, qtot], [ValveEGR, Xr,EGR], [pIMF, mair, ρIMF], [ρSOC,pil, ρSOC,main], [TSOC,pil, TSOC,main] and [SOCpil, SOCmain]) are constituted by two variables which are closely correlated to each other. Therefore, only one variable should be selected as representative of each group;
- the total number of independent variable candidates should not be too high (in this study a maximum of 15 variables was chosen for the estimation of each dependent one), in order to ensure that the partial coefficient order is not too large and to make the model more robust to input uncertainty.
| Dependent Variable | Initial Candidate Set of the Independent Variables Selected Using Pearson Correlation Analysis |
|---|---|
| , , , , , , , , , | |
| , , , , , , , , , | |
| , , , , , , , , , , , , , , | |
| , , , , , , , , , , | |
| , , , , , , , , , , | |
| , , , , , , , , , , , , | |
| , , , , , , , , , , , , | |
| , , , , , , , , , , , , | |
| , , , , , , , , , , , | |
| , , , , , , , , , , , , , | |
| , , , , , , , , , , , , , | |
| , , , , , , , , , , , | |
| , , , , , , , , , , , | |
| PMEP | , , , , , , , , , |
| FMEP | , , , , , , , , , , , , |
| , , , , , , , , , , |
| Dependent Variable | Initial Candidate of the Independent Variables | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Independent variable | ||||||||||||||||
| Pearson coefficient | 0.10 | −0.43 | −0.28 | −0.41 | −0.77 | −0.51 | −0.08 | 0.31 | −0.62 | −0.57 | ||||||
| Partial coefficient | −0.46 | −0.56 | −0.47 | −0.48 | −0.29 | −0.24 | 0.19 | −0.50 | 0.42 | 0.21 | ||||||
| Independent variable | ||||||||||||||||
| Pearson coefficient | 0.80 | 0.29 | −0.89 | −0.73 | 0.06 | 0.11 | −0.01 | 0.43 | −0.71 | −0.81 | ||||||
| Partial coefficient | 0.44 | −0.37 | −0.13 | −0.06 | −0.15 | 0.13 | −0.16 | 0.12 | −0.05 | 0.44 | ||||||
| Independent variable | ||||||||||||||||
| Pearson coefficient | 0.31 | −0.32 | −0.50 | −0.40 | −0.70 | 0.18 | −0.58 | 0.45 | 0.58 | −0.78 | −0.63 | −0.58 | −0.40 | 0.33 | 0.68 | |
| Partial coefficient | 0.26 | −0.47 | −0.27 | 0.03 | −0.18 | −0.01 | −0.05 | −0.01 | −0.13 | 0.34 | −0.29 | 0.06 | 0.00 | 0.08 | 0.26 | |
| Independent variable | ||||||||||||||||
| Pearson coefficient | 0.35 | 0.10 | −0.47 | −0.30 | −0.04 | −0.14 | 0.25 | −0.40 | −0.51 | 0.65 | 0.35 | |||||
| Partial coefficient | −0.45 | 0.36 | 0.02 | −0.01 | 0.13 | −0.15 | −0.07 | −0.13 | 0.10 | 0.76 | −0.16 | |||||
| Independent variable | ||||||||||||||||
| Pearson coefficient | −0.13 | −0.44 | −0.22 | −0.51 | 0.18 | −0.39 | −0.15 | 0.14 | 0.75 | −0.33 | −0.36 | |||||
| Partial coefficient | −0.34 | 0.13 | −0.20 | 0.04 | −0.44 | −0.19 | 0.15 | −0.26 | −0.12 | −0.49 | 0.69 | |||||
| Independent variable | ||||||||||||||||
| Pearson coefficient | −0.02 | 0.32 | 0.11 | 0.36 | 0.52 | −0.16 | 0.36 | −0.41 | −0.75 | 0.34 | 0.30 | −0.16 | −0.68 | |||
| Partial coefficient | 0.01 | −0.06 | −0.09 | −0.17 | −0.20 | 0.13 | −0.06 | −0.50 | 0.21 | −0.27 | −0.10 | −0.27 | 0.01 | |||
| Independent variable | ||||||||||||||||
| Pearson coefficient | −0.23 | 0.25 | 0.40 | 0.60 | 0.94 | −0.35 | 0.70 | −0.72 | −0.61 | 0.84 | 0.60 | −0.70 | 0.52 | |||
| Partial coefficient | 0.33 | −0.48 | 0.40 | −0.04 | 0.93 | −0.44 | −0.08 | 0.34 | 0.14 | −0.43 | −0.24 | −0.42 | 0.09 | |||
| Independent variable | ||||||||||||||||
| Pearson coefficient | 0.37 | −0.04 | −0.54 | −0.42 | −0.43 | 0.31 | −0.36 | 0.34 | 0.36 | −0.57 | −0.33 | −0.38 | 0.32 | |||
| Partial coefficient | 0.07 | −0.14 | −0.31 | 0.04 | −0.01 | −0.07 | −0.27 | 0.03 | −0.03 | 0.26 | 0.09 | −0.06 | 0.07 | |||
| Independent variable | ||||||||||||||||
| Pearson coefficient | 0.57 | 0.86 | −0.36 | −0.33 | 0.75 | 0.98 | −0.52 | 0.45 | 0.90 | −0.35 | 0.95 | 0.47 | ||||
| Partial coefficient | −0.09 | −0.13 | 0.06 | −0.03 | −0.02 | 0.42 | −0.02 | −0.09 | 0.16 | −0.12 | −0.15 | 0.18 | ||||
| Independent variable | ||||||||||||||||
| Pearson coefficient | −0.49 | −0.21 | 0.39 | 0.35 | 0.29 | −0.03 | −0.45 | −0.27 | 0.39 | 0.13 | 0.21 | −0.25 | −0.47 | −0.54 | ||
| Partial coefficient | −0.45 | 0.09 | −0.15 | −0.28 | 0.24 | −0.19 | 0.19 | −0.01 | −0.01 | 0.13 | −0.05 | 0.03 | −0.42 | −0.16 | ||
| Independent variable | ||||||||||||||||
| Pearson coefficient | −0.48 | −0.71 | 0.27 | −0.06 | −0.77 | 0.19 | 0.68 | 0.65 | −0.76 | −0.72 | 0.36 | −0.27 | 0.69 | −0.53 | ||
| Partial coefficient | −0.69 | −0.13 | −0.04 | −0.24 | −0.36 | 0.05 | 0.04 | −0.04 | 0.07 | 0.05 | −0.03 | 0.25 | 0.52 | 0.20 | ||
| Independent variable | ||||||||||||||||
| Pearson coefficient | 0.11 | 0.38 | 0.54 | 0.17 | 0.69 | 0.57 | −0.42 | −0.54 | 0.58 | 0.73 | 0.73 | 0.26 | ||||
| Partial coefficient | 0.76 | −0.64 | 0.84 | 0.07 | 0.35 | 0.13 | −0.10 | −0.10 | 0.07 | −0.10 | 0.16 | 0.13 | ||||
| Independent variable | ||||||||||||||||
| Pearson coefficient | 0.30 | 0.76 | −0.21 | 0.02 | 0.87 | 0.89 | −0.65 | −0.64 | 0.90 | 0.55 | 0.85 | −0.24 | ||||
| Partial coefficient | −0.68 | 0.59 | −0.69 | 0.21 | 0.36 | −0.32 | −0.10 | −0.13 | 0.35 | −0.20 | −0.25 | 0.30 | ||||
| Independent variable | ||||||||||||||||
| Pearson coefficient | 0.96 | 0.71 | −0.86 | −0.84 | 0.51 | 0.10 | −0.19 | −0.78 | 0.77 | 0.97 | ||||||
| Partial coefficient | 0.57 | −0.05 | −0.58 | 0.25 | 0.32 | 0.09 | 0.04 | −0.21 | −0.05 | 0.84 | ||||||
| Independent variable | ||||||||||||||||
| Pearson coefficient | 0.90 | 0.86 | −0.74 | −0.67 | 0.33 | 0.76 | 0.10 | −0.30 | 0.56 | 0.56 | 0.56 | −0.68 | 0.79 | |||
| Partial coefficient | 0.28 | 0.08 | −0.03 | 0.18 | −0.25 | 0.15 | 0.15 | −0.18 | −0.28 | −0.00 | 0.25 | −0.04 | −0.07 | |||
| Independent variable | ||||||||||||||||
| Pearson coefficient | −0.05 | 0.49 | 0.27 | 0.41 | 1.00 | −0.23 | 0.83 | −0.64 | −0.78 | 0.87 | 0.88 | |||||
| Partial coefficient | −0.78 | 0.51 | −0.64 | 0.43 | 0.97 | −0.01 | −0.07 | −0.11 | −0.43 | 0.20 | 0.61 | |||||
Appendix B. Training and Selection of the ANNs




| Algorithm A1. Automatic selection |
| for i = 1:200 if i = 1 ANN_best = ANN_i; R2_best = [ R2(i,1), R2 (i,2), R2 (i,3)]; MSE_best = [ MSE (i,1), MSE (i,2), MSE (i,3)]; else if R2(i,3) > R2_best(3) && (R2 (i,2) > R2_best(2) || R2 (i,1) > R2_best(1)) && abs(R2 (i,1)−R2(i,2)) < 0.10* R2_best(3) ANN_best = ANN_i; R2_best = [ R2(i,1), R2 (i,2), R2 (i,3)]; MSE_best = [ MSE (i,1), MSE (i,2), MSE (i,3)]; end end end |




References
- Payri, F.; Olmeda, P.; Martín, J.; García, A. A complete 0D thermodynamic predictive model for direct injection diesel engines. Appl. Energy 2011, 88, 4632–4641. [Google Scholar] [CrossRef]
- Maroteaux, F.; Saad, C.; Aubertin, F. Development and validation of double and single Wiebe function for multi-injection mode Diesel engine combustion modelling for hardware-in-the-loop applications. Energy Convers. Manag. 2015, 105, 630–641. [Google Scholar] [CrossRef]
- Hu, S.; Wang, H.; Niu, X.; Li, X.; Wang, Y. Automatic calibration algorithm of 0-D combustion model applied to DICI diesel engine. Appl. Therm. Eng. 2018, 130, 331–342. [Google Scholar] [CrossRef]
- Ferrari, A.; Mittica, A.; Pizzo, P.; Jin, Z. PID Controller Modelling and Optimization in Cr Systems with Standard and Reduced Accumulators. Int. J. Automot. Technol. 2018, 19, 771–781. [Google Scholar] [CrossRef]
- Ferrari, A.; Mittica, A.; Pizzo, P.; Wu, X.; Zhou, H. New methodology for the identification of the leakage paths and guidelines for the design of common rail injectors with reduced leakage. J. Eng. Gas Turbines Power 2018, 140, 022801. [Google Scholar] [CrossRef]
- Ferrari, A.; Mittica, A.; Paolicelli, F.; Pizzo, P. Hydraulic Characterization of Solenoid-actuated Injectors for Diesel Engine Common Rail Systems. Energy Procedia 2016, 101, 878–885. [Google Scholar] [CrossRef]
- Catania, A.E.; Ferrari, A.; Mittica, A.; Spessa, E. Common Rail without Accumulator: Development, Theoretical-Experimental Analysis and Performance Enhancement at DI-HCCI Level of a New Generation FIS. SAE Tech. Paper Ser. 2007. [Google Scholar] [CrossRef]
- Catania, A.; Ferrari, A.; Mittica, A. High-pressure rotary pump performance in multi-jet common rail systems. In Proceedings of the 8th Biennial ASME Conference on Engineering Systems Design and Analysis; ESDA2006, Engineering Systems Design and Analysis, Fatigue and Fracture, Heat Transfer, Internal Combustion Engines, Manufacturing, and Technology and Society, Torino, Italy, 4–7 July 2006; Volume 4, pp. 557–565. [Google Scholar] [CrossRef]
- Baratta, M.; Finesso, R.; Misul, D.; Spessa, E. Comparison between Internal and External EGR Performance on a heavy Duty Diesel Engine by Means of a Refined 1D Fluid-Dynamic Engine Model. SAE Int. J. Engines 2015, 8, 1977–1992. [Google Scholar] [CrossRef]
- D’Ambrosio, S.; Gaia, F.; Iemmolo, D.; Mancarella, A.; Salamone, N.; Vitolo, R.; Hardy, G. Performance and Emission Comparison between a Conventional Euro VI Diesel Engine and an Optimized PCCI Version and Effect of EGR Cooler Fouling on PCCI Combustion. SAE Tech. Paper Ser. 2018. [Google Scholar] [CrossRef]
- Finesso, R.; Marello, O.; Misul, D.; Spessa, E.; Violante, M.; Yang, Y.; Hardy, G.; Maier, C. Development and Assessment of Pressure-Based and Model-Based Techniques for the MFB50 Control of a Euro VI 3.0L Diesel Engine. SAE Int. J. Engines 2017, 10, 1538–1555. [Google Scholar] [CrossRef]
- Finesso, R.; Marello, O.; Spessa, E.; Yang, Y.; Hardy, G. Model-Based Control of BMEP and NOx Emissions in a Euro VI 3.0L Diesel Engine. SAE Int. J. Engines 2017, 10, 2288–2304. [Google Scholar] [CrossRef]
- Finesso, R.; Spessa, E.; Yang, Y.; Conte, G.; Merlino, G. Neural-Network Based Approach for Real-Time Control of BMEP and MFB50 in A Euro 6 Diesel Engine; SAE Technical Paper 2017-24-0068; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Finesso, R.; Hardy, G.; Mancarella, A.; Marello, O.; Mittica, A.; Spessa, E. Real-Time Simulation of Torque and Nitrogen Oxide Emissions in an 11.0 L Heavy-Duty Diesel Engine for Model-Based Combustion Control. Energies 2019, 12, 460. [Google Scholar] [CrossRef]
- Hu, S.; Wang, H.; Sun, Y.; Wang, Y. Zero-Dimensional Prediction Combustion Modelling of a Turbocharging Diesel Engine. Trans. CSICE 2016, 34, 311–318. [Google Scholar] [CrossRef]
- Catania, A.E.; Finesso, R.; Spessa, E. Predictive zero-dimensional combustion model for DI diesel engine feed-forward control. Energy Convers. Manag. 2011, 52, 3159–3175. [Google Scholar] [CrossRef]
- Finesso, R.; Spessa, E.; Yang, Y. Development and Validation of a Real-Time Model for the Simulation of the Heat Release Rate, In-Cylinder Pressure and Pollutant Emissions in Diesel Engines. SAE Int. J. Engines 2016, 9, 322–341. [Google Scholar] [CrossRef]
- Orthaber, G.C.; Chmela, F.G. Rate of Heat Release Prediction for Direct Injection Diesel Engines Based on Purely Mixing Controlled Combustion; SAE Technical Paper 1999-01-0186; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Egnell, R. A Simple Approach to Studying the Relation between Fuel Rate Heat Release Rate and NO Formation in Diesel Engines; SAE Technical Paper 1999-01-3548; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Ericson, C.; Westerberg, B. Modelling Diesel Engine Combustion and NOx Formation for Model Based Control and Simulation of Engine and Exhaust Aftertreatment Systems; SAE Technical Paper 2006-01-0687; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Finesso, R.; Spessa, E.; Yang, Y.; Alfieri, V.; Conte, G. HRR and MFB50 Estimation in a Euro 6 Diesel Engine by Means of Control-Oriented Predictive Models. SAE Int. J. Engines 2015, 8, 1055–1068. [Google Scholar] [CrossRef]
- Hu, S.; Wang, H.; Yang, C.; Wang, Y. Burnt fraction sensitivity analysis and 0-D modelling of common rail diesel engine using Wiebe function. Appl. Therm. Eng. 2017, 115, 170–177. [Google Scholar] [CrossRef]
- Finesso, R.; Spessa, E.; Yang, Y. Fast estimation of combustion metrics in DI diesel engines for control-oriented applications. Energy Convers. Manag. 2016, 112, 254–273. [Google Scholar] [CrossRef]
- Roy, S.; Ghosh, A.; Das, A.K.; Banerjee, R. A comparative study of GEP and an ANN strategy to model engine performance and emission characteristics of a CRDI assisted single cylinder diesel engine under CNG dual-fuel operation. J. Nat. Gas Sci. Eng. 2014, 21, 814–828. [Google Scholar] [CrossRef]
- Brusca, S.; Lanzafame, R.; Messina, M. A Combustion Model for ICE by Means of Neural Network; SAE Technology Paper 2005-01-2110; SAE International: Warrendale, PA, USA, 2005. [Google Scholar] [CrossRef]
- Yusri, I.; Majeed, A.A.; Mamat, R.; Ghazali, M.; Awad, O.I.; Azmi, W. A review on the application of response surface method and artificial neural network in engine performance and exhaust emissions characteristics in alternative fuel. Renew. Sustain. Energy Rev. 2018, 90, 665–686. [Google Scholar] [CrossRef]
- Niu, X.; Yang, C.; Wang, H.; Wang, Y. Investigation of ANN and SVM based on limited samples for performance and emissions prediction of a CRDI-assisted marine diesel engine. Appl. Therm. Eng. 2017, 111, 1353–1364. [Google Scholar] [CrossRef]
- Turkson, R.F.; Yan, F.; Ali, M.K.A.; Hu, J. Artificial neural network applications in the calibration of spark-ignition engines: An overview. Eng. Sci. Technol. Int. J. 2016, 19, 1346–1359. [Google Scholar] [CrossRef] [Green Version]
- Yap, W.K.; Karri, V. ANN virtual sensors for emissions prediction and control. Appl. Energy 2011, 88, 4505–4516. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, D.-L.; Tian, Y.; Shi, Y. Air–fuel ratio prediction and NMPC for SI engines with modified Volterra model and RBF network. Eng. Appl. Artif. Intell. 2015, 45, 313–324. [Google Scholar] [CrossRef]
- Kshirsagar, C.M.; Anand, R. Artificial neural network applied forecast on a parametric study of Calophyllum inophyllum methyl ester-diesel engine out responses. Appl. Energy 2017, 189, 555–567. [Google Scholar] [CrossRef]
- Xu, K.; Xie, M.; Tang, L.; Ho, S. Application of neural networks in forecasting engine systems reliability. Appl. Soft Comput. 2003, 2, 255–268. [Google Scholar] [CrossRef]
- Pai, P.S.; Rao, B.S. Artificial Neural Network based prediction of performance and emission characteristics of a variable compression ratio CI engine using WCO as a biodiesel at different injection timings. Appl. Energy 2011, 88, 2344–2354. [Google Scholar]
- Kiani, M.K.D.; Ghobadian, B.; Tavakoli, T.; Nikbakht, A.; Najafi, G. Application of artificial neural networks for the prediction of performance and exhaust emissions in SI engine using ethanol- gasoline blends. Energy 2010, 35, 65–69. [Google Scholar] [CrossRef]
- Javed, S.; Murthy, Y.S.; Baig, R.U.; Rao, D.P. Development of ANN model for prediction of performance and emission characteristics of hydrogen dual fueled diesel engine with Jatropha Methyl Ester biodiesel blends. J. Nat. Gas Sci. Eng. 2015, 26, 549–557. [Google Scholar] [CrossRef]
- Bahri, B.; Shahbakhti, M.; Kannan, K.; Aziz, A.A. Identification of ringing operation for low temperature combustion engines. Appl. Energy 2016, 171, 142–152. [Google Scholar] [CrossRef]
- Lawrence, S.; Giles, C. Overfitting and neural networks: Conjugate gradient and backpropagation. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27 June 2000; Volume 1, pp. 114–119. [Google Scholar]
- Finesso, R.; Hardy, G.; Maino, C.; Marello, O.; Spessa, E. A New Control-Oriented Semi-Empirical Approach to Predict Engine-Out NOx Emissions in a Euro VI 3.0 L Diesel Engine. Energies 2017, 10, 1978. [Google Scholar] [CrossRef]
- Heywood, J. Internal Combustion Engine Fundamentals; McGraw-Hill Intern: Columbus, OH, USA, 1988. [Google Scholar]
- Chen, S.K.; Flynn, P.F. Development of a Single Cylinder Compression Ignition Research Engine; SAE Technical SAE Technical Paper 650733; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Catania, A.; Finesso, R.; Spessa, E. Real-Time Calculation of EGR Rate and Intake Charge Oxygen Concentration for Misfire Detection in Diesel Engines; SAE Technical SAE Technical Pape r2011-24-0149; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Pearson, K. Contributions to the mathematical theory of evolution. Philos. Trans. R. Soc. Lond. A 1894, 185, 71–110. [Google Scholar] [CrossRef]
- Wilson, L.T. Pearson Product-Moment Correlation. Available online: https://explorable.com/pearson-product-moment-correlation?gid=1586 (accessed on 3 June 2018).
- Melissa, A.S.; Raghuraj, K.R.; Lakshminarayanan, S. Partial correlation metric based classifier for food product characterization. J. Food Eng. 2009, 90, 146–152. [Google Scholar] [CrossRef]
- Marrelec, G.; Krainik, A.; Duffau, H.; Pélégrini-Issac, M.; Lehéricy, S.; Doyon, J.; Benali, H. Partial correlation for functional brain interactivity investigation in functional MRI. NeuroImage 2006, 32, 228–237. [Google Scholar] [CrossRef]
- Rezaei, J.; Shahbakhti, M.; Bahri, B.; Aziz, A.A. Performance prediction of HCCI engines with oxygenated fuels using artificial neural networks. Appl. Energy 2015, 138, 460–473. [Google Scholar] [CrossRef]
- Najafi, G.; Ghobadian, B.; Tavakoli, T.; Buttsworth, D.; Yusaf, T.; Faizollahnejad, M. Performance and exhaust emissions of a gasoline engine with ethanol blended gasoline fuels using artificial neural network. Appl. Energy 2009, 86, 630–639. [Google Scholar] [CrossRef]
- MATLAB Documentation. Matlab User Guide; The MathWorks, Inc.: Natick, MA, USA, 2016. [Google Scholar]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network Toolbox™ User’s Guide; The MathWorks, Inc.: Natick, MA, USA, 2018. [Google Scholar]
- Ismail, H.M.; Ng, H.K.; Queck, C.W.; Gan, S. Artificial neural networks modelling of engine-out responses for a light-duty diesel engine fuelled with biodiesel blends. Appl. Energy 2012, 92, 769–777. [Google Scholar] [CrossRef]
- Yusaf, T.F.; Buttsworth, D.; Saleh, K.H.; Yousif, B.; Yousif, B. CNG-diesel engine performance and exhaust emission analysis with the aid of artificial neural network. Appl. Energy 2010, 87, 1661–1669. [Google Scholar] [CrossRef]
- Roy, S.; Banerjee, R.; Bose, P.K. Performance and exhaust emissions prediction of a CRDI assisted single cylinder diesel engine coupled with EGR using artificial neural network. Appl. Energy 2014, 119, 330–340. [Google Scholar] [CrossRef]
- Sayin, C.; Ertunc, H.M.; Hosoz, M.; Kilicaslan, I.; Canakci, M. Performance and exhaust emissions of a gasoline engine using artificial neural network. Appl. Therm. Eng. 2007, 27, 46–54. [Google Scholar] [CrossRef]
- Baum, E.B.; Haussler, D. What Size Net Gives Valid Generalization? Adv. Neural Inf. Process. Syst. 1989, 1, 81–90. [Google Scholar] [CrossRef]









| Engine Type | Number of Cylinders | Displace Ment | Bore × Stroke | Rod Length | Compres Sion Ratio | Valves per Cylinder | Turbo-Charger | Fuel Injection System |
|---|---|---|---|---|---|---|---|---|
| FPT F1C Euro VI diesel engine | 4 | 2998 cm3 | 95.8 mm × 104 mm | 160 mm | 17.5 | 4 | VGT type | High pressure Common Rail |
| Submodel | Calibration Parameter |
|---|---|
| Heat release model | Kpil,j; K1,main; K2,main; τpil,j; τmain |
| Net energy release model | Qf,evap; Qht,glob |
| Pressure model | ΔpIMF; n; n’ |
| BMEP model | FMEP, PMEP |
| Input Parameters (Directly Measured Quantities) | Generated Quantities Which Can Be Used as Input Parameters | Dependent Output Variables (RAF + Calibration Parameters of the Physics-Based Model) | Dependent Output Variables (Combustion Metrics for Use for Model-Based Control) |
|---|---|---|---|
| MFB50 | |||
| PFP | |||
| ρIMF | BMEP | ||
| pEMF | |||
| TEMF | |||
| PMEP | |||
| FMEP | |||
| IMEP360 | |||
| IMEP720 | |||
| Dependent Variable | Final List of the Independent Variables | Fitted Correlation | |
|---|---|---|---|
| , , , | 0.98, 0.135, 5.8% | ||
| , , , | 0.906, 1.06, 26.9% | ||
| , , , , | 0.886, 0.339, 47.9% | ||
| , , , , , | 0.365, 0.0894, 40.4% | ||
| , , , , , | 0.833, 0.0026, 5.4% | ||
| , , , , | 0.634, 0.0311, 61.5% | ||
| , , , , , | 0.532, 0.00145, 15.5% | ||
| , , , , , , | 0.654, 0.0053,0.39% | ||
| , , , , | 0.913, 0.01, 0.8% | ||
| , , , | 0.99, 0.0143, 11.5% | ||
| , , | 0.966, 0.00733, 4.6% 0.967, 0.00723, 4.37% | ||
| PMEP | , , , | 0.994, 0.0204, 14.4% | |
| FMEP | , , , | 0.939, 0.0978, 7.91% |
| Dependent Variable | Final List of the Independent Variables | Fitted Correlation | |
|---|---|---|---|
| , , , , , , | 0.974, 0.633, 0.17% | ||
| , , , , , , | 0.983, 3.03, 3.63% | ||
| , , , , , , , | 0.996, 0.257, 14.9% |
| Parameter | Selected Option |
|---|---|
| Network type | Feed-forward back-propagation |
| Hidden layer | Single layer |
| Process function | mapminmax |
| Training algorithm | trainbr |
| Transfer function | tansig |
| Loss function | MSE |
| Performance | MSE, |
| (a) Physics-Based Model Parameters | ||||||||||||
| Dependent Parameter | ΔpIMF | PMEP | FMEP | |||||||||
| Suitable number of neurons | 6 | 6 | 6 | 6 | 6 | 4 | 5 | 7 | 5 | 5 | 5 | 4 |
| Mean value of the training and testing | 0.977, 0.978 | 0.981, 0.983 | 0.889, 0.794 | 0.975, 0.968 | 0.939, 0.945 | 0.998, 0.998 | 0.914, 0.899 | 0.992, 0.995 | 0.977, 0.975 | 0.989, 0.989 | 1.00, 1.00 | 0.988, 0.986 |
| Mean value of the training and testing MSE | 0.53, 0.57 | 0.038, 0.063 | 0.0026, 0.0034 | 2 × 10−6, 2.6 × 10−6 | 3.15 × 10−4, 2.95 × 10−4 | 8.1 × 10−5, 9.6 × 10−5 | 7.2 × 10−7, 9.0 × 10−7 | 2.4 × 10−4, 2.2 × 10−4 | 3.6 × 10−6, 4.3 × 10−6 | 2.6 × 10−5, 2.6 × 10−5 | 5.7 × 10−5, 6.96 × 10−5 | 3.9 × 10−3, 3.9 × 10−3 |
| (b) Combustion Metrics | ||||||||||||
| Dependent Parameter | ||||||||||||
| Suitable number of neurons | 5 | 6 | 5 | |||||||||
| Mean value of the training and testing | 0.999, 0.999 | 1.00, 1.00 | 1.00, 1.00 | |||||||||
| Mean value of the training and testing | 0.030, 0.043 | 0.27, 0.40 | 0.0007, 0.0011 | |||||||||
| Dependent Parameter | ΔpIMF | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Most suitable number of neurons | 6 | 6 | 6 | 6 | 6 | 5 | 4 | 5 | 5 | 7 | 5 | 4 |
| The training and testing for ANNs | 0.977, 0.975 | 0.977, 0.974 | 0.878, 0.872 | 0.981, 0.973 | 0.941, 0.910 | 0.919, 0.917 | 0.998, 0.998 | 0.978, 0.974 | 0.989, 0.986 | 0.992, 0.991 | 1.00, 0.999 | 0.975, 0.978 |
| for the power-law based functions | 0.908 | 0.886 | 0.365 | 0.833 | 0.663 | 0.532 | 0.99 | 0.654 | 0.923 | 0.967 | 0.994 | 0.939 |
| Model Type | Steady-State Condition (R2 and RMSE) | WHTC Transient Condition (RMSE) | ||||
|---|---|---|---|---|---|---|
| Baseline physics-based model | 0.975 0.63 deg | 0.995 1.8 bar | 0.998 0.15 bar | 1.2 deg | 10.5 bar | 0.7 bar |
| ANN physics-based model | 0.984 0.48 deg | 0.995 1.6 bar | 0.998 0.17 bar | 1.2 deg | 13.8 bar | 0.8 bar |
| Direct semi-empirical model | 0.974 0.63 deg | 0.983 3.0 bar | 0.996 0.26 bar | 1.4 deg | 11.7 bar | 0.8 bar |
| Direct ANN model | 0.996 0.25 deg | 0.999 0.85 bar | 1.0 0.071 bar | 1.1 deg | 9.6 bar | 0.7 bar |
| Model | Calculated Quantity | Average Computational Time, per Iteration, on the ETAS ES910 Device. The Reported Computational Time Values are Cumulative. |
|---|---|---|
| Baseline physics-based model | MFB50 | ≈200 μs |
| PFP | ≈350 μs | |
| BMEP | ≈350 μs | |
| Direct semi-empirical model | MFB50 | <50 μs |
| PFP | <50 μs | |
| BMEP | <50 μs | |
| Direct ANN model | MFB50 | <50 μs |
| PFP | <50 μs | |
| BMEP | <50 μs |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; d’Ambrosio, S.; Finesso, R.; Manelli, A.; Marzano, M.R.; Mittica, A.; Ventura, L.; Wang, H.; Wang, Y. Comparison of Physics-Based, Semi-Empirical and Neural Network-Based Models for Model-Based Combustion Control in a 3.0 L Diesel Engine. Energies 2019, 12, 3423. https://doi.org/10.3390/en12183423
Hu S, d’Ambrosio S, Finesso R, Manelli A, Marzano MR, Mittica A, Ventura L, Wang H, Wang Y. Comparison of Physics-Based, Semi-Empirical and Neural Network-Based Models for Model-Based Combustion Control in a 3.0 L Diesel Engine. Energies. 2019; 12(18):3423. https://doi.org/10.3390/en12183423
Chicago/Turabian StyleHu, Song, Stefano d’Ambrosio, Roberto Finesso, Andrea Manelli, Mario Rocco Marzano, Antonio Mittica, Loris Ventura, Hechun Wang, and Yinyan Wang. 2019. "Comparison of Physics-Based, Semi-Empirical and Neural Network-Based Models for Model-Based Combustion Control in a 3.0 L Diesel Engine" Energies 12, no. 18: 3423. https://doi.org/10.3390/en12183423
APA StyleHu, S., d’Ambrosio, S., Finesso, R., Manelli, A., Marzano, M. R., Mittica, A., Ventura, L., Wang, H., & Wang, Y. (2019). Comparison of Physics-Based, Semi-Empirical and Neural Network-Based Models for Model-Based Combustion Control in a 3.0 L Diesel Engine. Energies, 12(18), 3423. https://doi.org/10.3390/en12183423