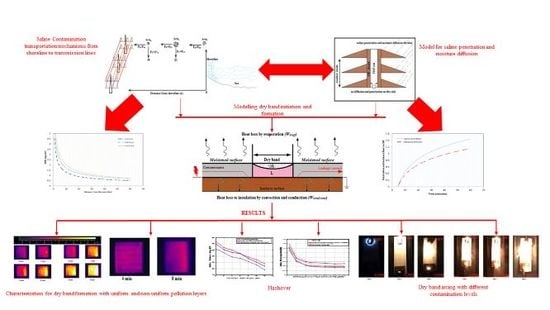
Mechanism of Saline Deposition and Surface Flashover on High-Voltage Insulators near Shoreline: Mathematical Models and Experimental Validations
Abstract
:1. Introduction
2. Mechanism of Salt Transportation and Deposition
2.1. Production of Saline
2.2. Saline Transportation and Deposition
2.3. Saline Penetration and Moisture Diffusion
3. Modelling of Dry Band Initiation and Formation
- WLC = Energy generated by leakage current
- W∆T = Energy generated by change in temperature
- Wevap. = Energy loss by evaporation due to ambient temperature
- Wcond./conv. = Energy loss by convection and conduction
4. Partial Arc Electric Model of Dry-Band Flashover
5. Experimental Setup and Results
Characteristics of Dry-Band Formation
6. Comparison of Models with Experimental Results
6.1. Inspection of Dry-Band Formation
6.2. Onset of Dry-Band Arcing
6.3. Impact of Wind Velocity on Surface Flashover Characteristics
6.4. Effect of Conductivity and Pollution Layer Length of Surface Flashover
7. Conclusions
- From simulation and experimental work it was found that the pollution accumulation rate on the insulator surface increases with the increase of wind velocity and decreases with the increase of distance from shoreline to inland. However, when wind speed was higher than 12 m/s, the contamination density tended to be constant.
- It was also observed that the transfer of moisture significantly accelerates the saline ions’ penetration on the insulator surface.
- The dry-band initiation and formation model presented is based on the energy balance equation. The integration of this equation results in a variation of dry-band length under moisture evaporation on the insulator surface. With the reduction of dry-band length, the surface resistance increases, which increases the discharge current on the insulator surface. The conduction and convection processes increase the surface resistance. It was observed that under this process single and multiple dry bands appear on the insulator surface.
- Discontinuous non-uniform contamination distribution of the insulator surface leads to multiple dry bands and lower surface flashover voltage as compared to uniform and non-uniform contamination distribution.
- A dry band arcing model was developed. It showed that the insulator surface strength and arc length mainly depend on the distribution of the pollution layer and leakage distance. The results obtained show that the configured scenarios are trustworthy to detect the dry band arcing on the insulator surface with different contamination distribution. The obtained dry-band arcing initiation and elongation rate confirm the efficiency of the proposed model.
Author Contributions
Funding
Conflicts of Interest
References
- Venkataraman, S.; Gorur, R.S. Extending the applicability of insulator flashover models by regression analysis. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 368–374. [Google Scholar] [CrossRef]
- Baker, A.C.; Farzaneh, M.; Gorur, R.S.; Gubanski, S.M.; Hill, R.J.; Schneider, H.M. Insulator selection for overhead AC lines with respect to contamination. IEEE Trans. Power Deliv. 2009, 24, 1633–1641. [Google Scholar] [CrossRef]
- El-Amine Slama, M.; Hadi, H.; Flazi, S. Investigation on influence of salts mixture on the determination of flashover discharge constant Part I: A Preliminary Study. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena, Quebec, QC, Canada, 26–29 October 2008; pp. 674–677. [Google Scholar]
- Sima, W.; Yuan, T.; Yang, Q.; Xu, K.; Sun, C. Effect of nonuniform pollution on the withstand characteristics of extra high voltage suspension ceramic insulator string. IET Gen. Trans. Distrib. 2009, 4, 445–455. [Google Scholar] [CrossRef]
- Majid Hussain, M.; Farokhi, S.; McMeekin, S.G.; Farzaneh, M. Dry band formation on HV insulators polluted with different salt mixtures. In Proceedings of the 2015 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Ann Arbor, MI, USA, 18–21 October 2015; pp. 201–204. [Google Scholar]
- Naito, K.; Morita, K.; Hasegawa, Y.; Imakoma, T. Improvement of the dc voltage insulation efficiency of suspension insulators under contaminated conditions. IEEE Trans. Dielectr. Electr. Insul. 1988, 23, 1025–1032. [Google Scholar] [CrossRef]
- Seta, T.; Arai, N.; Udo, T. Natural pollution test of insulators energized with HVDC. IEEE Trans. Power Appar. Syst. 1974, PAS-93, 878–883. [Google Scholar] [CrossRef]
- Kimoto, I.; Fujimura, T.; Naito, K. Performance of insulators for direct current transmission line under polluted condition. IEEE Trans. Power Appar. Syst. 1973, PAS-92, 943–949. [Google Scholar] [CrossRef]
- Houlgate, R.G.; Swift, D.A.; Cimador, A.; Pourbaix, F.; Marrone, G.; Nicolini, P. Field experience and laboratory research on composite insulators for overhead lines. CIGRE Pap. 1986, 15, 12. [Google Scholar]
- Schneider, H.M.; Guidi, W.W.; Burnham, J.T.; Gorur, R.S.; Hall, J.F. Accelerated aging and flashover tests on 138 kV nonceramic line post insulators. IEEE Trans. Power Deliv. 1993, 8, 325–336. [Google Scholar] [CrossRef]
- Kim, S.H.; Cherney, E.A.; Hackam, R. The loss and recovery of hydrophobicity of RTV silicone rubber insulator coatings. IEEE Trans. Power Deliv. 1990, 5, 1491–1500. [Google Scholar] [CrossRef]
- Starr, W.T. Polymeric outdoor insulation. IEEE Trans. Electr. Insul. 1990, 25, 125–136. [Google Scholar] [CrossRef]
- Simmons, S.; Shah, M.; Mackevich, J.; Chang, R.J. Polymer outdoor insulating materials Part 3-silicone elastomer considerations. IEEE Electr. Insul. Mag. 1997, 13, 25–32. [Google Scholar] [CrossRef]
- Baker, A.C.; Zaffanella, L.E.; Anaivino, L.D.; Schneider, H.M.; Moran, J.H. Contamination performance of HVDC station post insulators. IEEE Trans. Power Deliv. 1988, 3, 1968–1975. [Google Scholar] [CrossRef]
- Wilkins, R. Flashover voltage of high-voltage insulators with uniform surface pollution films. Proc. IEE 1969, 116, 457–465. [Google Scholar] [CrossRef]
- Rizk, F.A.M. Mathematical models for pollution flashover. IEEE Trans. Dielectr. Electr. Insul. 1981, 78, 71–103. [Google Scholar]
- Kim, S.; Cherney, E.A.; Hackam, R.; Rutherford, K.G. Chemical changes at the surface of RTV silicone rubber coating on insulators during dry-band arcing. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 106–123. [Google Scholar]
- Morcillo, M.; Chico, B.; Mariaca, L.; Otero, E. Salinity in marine atmospheric corrosion: Its dependence on the wind regime existing in the site. Corros. Sci. 2000, 42, 91–104. [Google Scholar] [CrossRef]
- Spiel, D.E.; Leeuw, G.D. Formation and production of sea spray aerosols. J. Aerosol Sci. 1996, 27, S65–S66. [Google Scholar] [CrossRef]
- Feliu, S.; Morcillo, M.; Chico, B. Effect of distance from sea on atmospheric corrosion rate. Corrosion 1999, 55, 883–889. [Google Scholar] [CrossRef]
- Gustafsson, M.E.R.; Franzen, L.G. Dry deposition and concentration of marine aerosols in a coastal area. Atmos. Environ. 1996, 30, 977–989. [Google Scholar] [CrossRef]
- Meira, R.; Andrade, C.; Alonso, C.; Padaradtz, I.J.; Borba, J.C. Salinity of marine aerosols in a Brazilian coastal area–influence of wind regime. Atmos. Environ. 2007, 41, 8431–8441. [Google Scholar] [CrossRef]
- Hamada, S.; Hino, S.; Kanyuki, K. Salt measurement in the coastal region. Fac. Eng. Yamaguchi Univ. 1986, 01, 255. [Google Scholar]
- Karady, G.; Amrah, F. Dynamic modeling of AC insulator flashover characteristics. IEE Symp. High Volt. Eng. 1999, 467, 107–110. [Google Scholar]
- Jolly, D.C.; Poole, C.D. Flashover of contaminated insulators with cylindrical symmetry under DC conditions. IEEE Trans. Dielectr. Electr. Insul. 1979, EI-14, 77–84. [Google Scholar] [CrossRef]
- Obenaus, F. Contamination flashover and creepage path length. Dtsch. Elektrotechnik 1958, 12, 135–136. [Google Scholar]
- Majid Hussain, M.; Farokhi, S.; McMeekin, S.G.; Farzaneh, M. Risk assessment of failure of outdoor high voltage polluted insulators under combined stresses near shoreline. Energies 2017, 10, 1661. [Google Scholar] [CrossRef]
- Mizuno, Y.; Kusada, H.; Naito, K. Effect of climatic conditions on contamination flashover voltage of insulators. IEEE Trans. Dielectr. Electr. Insul. 1997, 4, 286–289. [Google Scholar] [CrossRef]
- Majid Hussain, M.; Farokhi, S.; McMeekin, S.G.; Farzaneh, M. Contamination performance of high voltage outdoor insulators in harsh marine pollution environment. In Proceedings of the IEEE 21st International Conference on Pulsed Power, Brighton, UK, 18–22 June 2017. [Google Scholar]
- Majid Hussain, M.; Farokhi, S.; McMeekin, S.G.; Farzaneh, M. Mechanism of saline deposition and surface flashover on outdoor insulators near coastal areas Part II: Impact of various environmental stresses. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1068–1076. [Google Scholar] [CrossRef]
- Terrab, H.; Bayad, A. Experimental study using design of experiment of pollution layer effect on insulator performance taking into account the presence of dry bands. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 2486–2495. [Google Scholar] [CrossRef]
- Zohng, H.P.; Dong, X.C. Tests and Investigations on Naturally Polluted Insulators and Their Application to Insulation Design for Polluted Areas; CIGRE Report 33–07; CIGRE: Paris, France, 1982. [Google Scholar]
















| Insulator Type | Leakage Distance (cm) | Shed Spacing (cm) | Shed Diameter |
|---|---|---|---|
| Silicone rubber | 40 | 3 | 12 |
| Contamination Type | ESDD (mg/cm2) | NSDD (mg/cm2) |
|---|---|---|
| Uniform | 0.200 | 0.850 |
| Non-uniform | 0.080 | 0.350 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, M.M.; Chaudhary, M.A.; Razaq, A. Mechanism of Saline Deposition and Surface Flashover on High-Voltage Insulators near Shoreline: Mathematical Models and Experimental Validations. Energies 2019, 12, 3685. https://doi.org/10.3390/en12193685
Hussain MM, Chaudhary MA, Razaq A. Mechanism of Saline Deposition and Surface Flashover on High-Voltage Insulators near Shoreline: Mathematical Models and Experimental Validations. Energies. 2019; 12(19):3685. https://doi.org/10.3390/en12193685
Chicago/Turabian StyleHussain, Muhammad Majid, Muhammad Akmal Chaudhary, and Abdul Razaq. 2019. "Mechanism of Saline Deposition and Surface Flashover on High-Voltage Insulators near Shoreline: Mathematical Models and Experimental Validations" Energies 12, no. 19: 3685. https://doi.org/10.3390/en12193685
APA StyleHussain, M. M., Chaudhary, M. A., & Razaq, A. (2019). Mechanism of Saline Deposition and Surface Flashover on High-Voltage Insulators near Shoreline: Mathematical Models and Experimental Validations. Energies, 12(19), 3685. https://doi.org/10.3390/en12193685