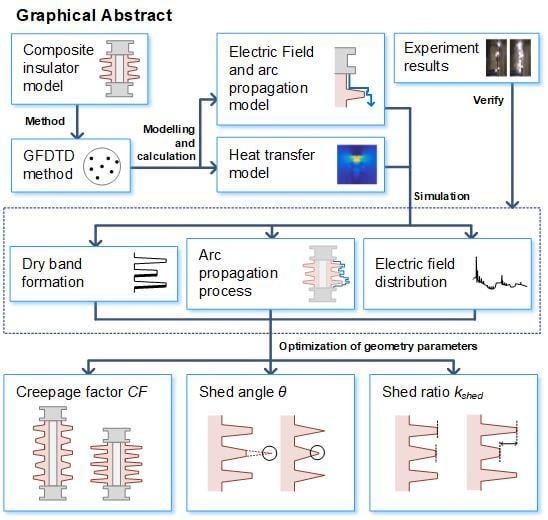
Modeling of Dry Band Formation and Arcing Processes on the Polluted Composite Insulator Surface
Abstract
:1. Introduction
2. Model Schematic and Method
2.1. Insulator Model Schematic
2.2. Dry Band Formation and Arc Propagation Models
2.2.1. Electric Field and Arc Propagation Model
2.2.2. Heat Transfer Model
3. Simulation Results
3.1. Dry Band Formation and Arcing Simulations
3.2. Experiment Results
4. Insulator Geometry Optimization
4.1. Creepage Factor Optimization
4.2. Shed Angle Optimization
4.3. Alternative Shed Ratio Optimization
5. Conclusions
- The GFDTD method is suitable to calculate the electric and thermal fields for the insulator geometry by improving the field calculation accuracy at the high precision requirement area and reducing the computational complexity at the low precision requirement area.
- The stochastic characteristics and the arc trajectory jumping between insulator sheds were modelled to simulate the physical phenomena of the arc.
- The maximum electric field decreases with the expansion of the dry band. The heat transfer model demonstrates that the leakage current density is the dominant factor to affect dry band formation before the arc initialization, while the arc radiation becomes the dominant factor to form the dry band after the arc ignition.
- The 50% flashover voltage of composite insulators increases with the decrease of the CF value and the increase of the alternative shed ratio. The duration time from the pollution layer generation moment to flashover increases with the decrease of the CF value and the increase of the alternative shed angle.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | coefficient matrix multiply with [Dφ] |
| (a−1)r,c | element at r-th row and c-th column of matrix [A]−1 |
| a(E − Ec) | step function of random walk |
| B | coefficient matrix multiply with [φ] |
| B(u) | residual function of two discrete points |
| b | constant matrix which equals to the product of [A] and [Dφ] |
| br, c | element at r-th row and c-th column of matrix [B] |
| c | specific heat capacity |
| CF | creepage factor |
| D | constant matrix which equals to the product of [A]−1 and [B] |
| Du | partial difference column matrix |
| d | insulator arcing distance |
| d1, 2, 3… | distance between two discrete points |
| dr, c | element at r-th row and c-th column of matrix [D] |
| E | electric field strength |
| Ec | RMS value of the threshold field |
| electric field strength in GFDTD form | |
| ESDDB | ESDD value of bottom part of the insulator |
| ESDDT | ESDD value of top part of the insulator |
| phase changing enthalpy of water | |
| h | heat transfer coefficient of convection |
| hij | absolute value X coordinate differences between two discrete points |
| J | leakage current density |
| leakage current density in GFDTD form | |
| kij | absolute value Y coordinate differences between two discrete points |
| kshed | ratio of radii of large and small sheds |
| l | length of insulator leakage distance |
| l1, l2 | insulator leakage distance |
| P | probability of random walk |
| P1, 2, 3… | discrete points |
| p1, p2 | saturated vapor pressure |
| R | universal gas constant |
| r1, r2 | radius of large and small sheds |
| T | thermal temperature |
| T0 | environment temperature |
| T1, T2 | thermal temperature change before and after arc initialization |
| t | time |
| t0 | time duration of insulator current leakage |
| u | column matrix of discrete point values |
| ui | value of field at a discrete point |
| V | volume |
| Warc_radiation | heat radiation energy of arcs |
| Wconduction | energy of heat conduction |
| Wconvention | energy of heat convention |
| Wleakage | energy of leakage current |
| Wwater_steam | required energy for water evaporation |
| w1, 2, 3… | weight function of discrete points in residual function |
| Γ | field boundary |
| ε | permittivity |
| εi | permittivity in GFDTD form |
| εemit | emissivity |
| θ | shed angle |
| λ | thermal conductivity |
| ρ | density |
| ρc | bulk charge density |
| bulk charge density in GFDTD form | |
| ρr | resistivity |
| σ | Stefan-Boltzmann constant |
| Φ | internal heat sources |
| Φi | internal heat sources in GFDTD form |
| φ | electric potential |
| electric potential in GFDTD form |
Appendix A

References
- Gorur, R.S.; Cherney, E.A.; Burnham, J.T. Outdoor Insulators; Ravi, S., Ed.; Gorur Inc.: Phoenix, AZ, USA, 1999. [Google Scholar]
- Gorur, R.S. Status Assessment of Composite Insulators for Outdoor HV Applications. In Proceedings of the 5th International Conference on Properties and Applications of Dielectric Materials, Seoul, Korea, 25–30 May 1997. [Google Scholar]
- Headley, P. Development and Application Experience with Composite Insulators for Overhead Lines. In Proceedings of the IEE Colloquium on Non-Ceramic Insulators for Overhead Lines, London, UK, 16 October 1992. [Google Scholar]
- Clift, S. Composite Fiber Optic Insulators and Their Application to High Voltage Sensor Systems. In Proceedings of the IEE Colloquium on Structural Use of Composites in High Voltage Switchgear/Transmission Networks, London, UK, 16 October 1992. [Google Scholar]
- Ilomuanya, C.S.; Nekahi, A.; Farokhi, S. Acid Rain Pollution Effect on the Electric Field Distribution of a Glass Insulator. In Proceedings of the 2018 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Athens, Greece, 10–13 September 2018. [Google Scholar]
- Liu, Y.; Wang, J.; Zhou, M.; Fang, C.; Zhou, W. Research on the Silicone Rubber Sheds Performance of Composite Insulator. In Proceedings of the 2008 International Conference on High Voltage Engineering and Application, Chongqing, China, 9–12 November 2008. [Google Scholar]
- Hussain, M.M.; Farokhi, S.; McMeekin, S.G.; Farzaneh, M. Effect of Cold Fog on Leakage Current Characteristics of Polluted Insulators. In Proceedings of the 2015 International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Bangalore, India, 10–12 December 2015. [Google Scholar]
- Hussain, M.M.; Farokhi, S.; McMeekin, S.G.; Farzaneh, M. Mechanism of Saline Deposition and Surface Flashover on Outdoor Insulators near Coastal Areas Part II: Impact of Various Environment Stresses. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1068–1076. [Google Scholar] [CrossRef]
- Hussain, M.; Farokhi, S.; McMeekin, S.G.; Farzaneh, M. Effect of Uneven Wetting on E-field Distribution along Composite Insulators. In Proceedings of the 2016 IEEE Electrical Insulation Conference (EIC), Montreal, QC, USA, 19–22 June 2016. [Google Scholar]
- Hussain, M.M.; Farokhi, S.; McMeekin, S.G.; Farzaneh, M. Dry Band Formation on HV Insulators Polluted with Different Salt Mixtures. In Proceedings of the 2015 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Ann Arbor, MI, USA, 18–21 October 2015. [Google Scholar]
- Nekahi, A.; McMeekin, S.G.; Farzaneh, M. Ageing and Degradation of Silicone Rubber Insulators due to Dry Band Arcing under Contaminated Conditions. In Proceedings of the 2017 52nd International Universities Power Engineering Conference (UPEC), Heraklion, Greece, 28–31 August 2017. [Google Scholar]
- Qiao, X.; Zhang, Z.; Jiang, X.; Li, X.; He, Y. A New Evaluation Method of Aging Properties for Silicon Rubber Material Based on Microscopic Images. IEEE Access 2019, 7, 15162–15169. [Google Scholar] [CrossRef]
- Kim, S.H.; Cherney, E.A.; Hackam, R. Effect of Dry Band Arcing on the Surface of RTV Silicone Rubber Coatings. In Proceedings of the Record of the 1992 IEEE International Symposium on Electrical Insulation, Baltimore, MD, USA, 7–10 June 1992. [Google Scholar]
- Qiao, X.; Zhang, Z.; Jiang, X.; Liang, T. Influence of DC Electric Fields on Pollution of HVDC Composite Insulator Short Samples with Different Environmental Parameters. Energies 2019, 12, 2304. [Google Scholar] [CrossRef]
- Hussain, M.M.; Chaudhary, M.A.; Razaq, A. Mechanism of Saline Deposition and Surface Flashover on High-Voltage Insulators near Shoreline: Mathematical Models and Experimental Validations. Energies 2019, 12, 3685. [Google Scholar] [CrossRef]
- Hussain, M.M.; Farokhi, S.; McMeekin, S.G.; Farzaneh, M. Observation of Surface Flashover Process on High Voltage Polluted Insulators near Shoreline. In Proceedings of the 2016 IEEE International Conference on Dielectrics (ICD), Montpellier, France, 3–7 July 2016. [Google Scholar]
- Hampton, B.F. Flashover Mechanism of Polluted Insulation. Proc. Inst. Electr. Eng. 1964, 111, 985–990. [Google Scholar] [CrossRef]
- Salthouse, E.C. Dry-Band Formation and Flashover in Uniform-Field Gaps. Proc. Inst. Electr. Eng. 1971, 118, 630. [Google Scholar] [CrossRef]
- Salthouse, E.C. Initiation of dry bands on polluted insulation. Proc. Inst. Electr. Eng. 1968, 115, 1707–1712. [Google Scholar] [CrossRef]
- Löberg, J.O.; Salthouse, E.C. Dry-Band Growth on Polluted Insulation. IEEE Trans. Electr. Insul. 1971, EI-6, 136–141. [Google Scholar]
- Zhou, J.; Gao, B.; Zhang, Q. Dry Band Formation and Its Influence on Electric Field Distribution along Polluted Insulator. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010. [Google Scholar]
- Das, A.; Ghosh, D.K.; Bose, R.; Chatterjee, S. Electric Stress Analysis of a Contaminated Polymeric Insulating Surface in Presence of Dry Bands. In Proceedings of the 2016 International Conference on Intelligent Control Power and Instrumentation (ICICPI), Kolkata, India, 21–23 October 2016. [Google Scholar]
- Benito, J.J.; Urena, F.; Gavate, L. Influence of Several Factors in the Generalized Finite Difference Method. Appl. Math. Model. 2001, 25, 1039–1053. [Google Scholar] [CrossRef]
- Gavete, L.; Gavate, M.L.; Benito, J.J. Improvements of Generalized Finite Difference Method and Comparison with Other Meshless Method. Appl. Math. Model. 2003, 27, 831–847. [Google Scholar] [CrossRef]
- Chen, J.; Gu, Y.; Wang, M.; Chen, W.; Liu, L. Application of the Generalized Finite Difference Method to Three-dimensional Transient Electromagnetic Problems. Eng. Anal. Bound. Elem. 2018, 92, 257–266. [Google Scholar] [CrossRef]
- Ureña, F.; Gavete, L.; García, A.; Benito, J.J.; Vargas, M. Solving Second Order Non-linear Parabolic PDEs Using Generalized Finite Difference Method (GFDM). J. Comput. Appl. Math. 2019, 354, 211–241. [Google Scholar] [CrossRef]
- Suchde, P.; Kuhnert, J.; Tiwari, S. On Meshfree GFDM Solvers for the Incompressible Navier–Stokes Equations. Comput. Fluids 2018, 165, 1–12. [Google Scholar] [CrossRef]
- Yee, K. Numerical Solution of Initial Boundary Value Problems Involving Maxwell’s Equations in Isotropic Media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Hou, K.; Li, W.; Ma, L.; Cheng, Y.; Jin, L. Multi-Objective Structural Optimization of UHV Composite Insulators based on Pareto Dominance. In Proceedings of the 2018 12th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Xi’an, China, 20–24 May 2018. [Google Scholar]
- Li, L. Shed Parameters Optimization of Composite Post Insulators for UHV DC Flashover Voltages at High Altitudes. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 169–176. [Google Scholar] [CrossRef]
- Doufene, D.; Bouazabia, S.; Ladjici, A.A. Shape Optimization of a Cap and Pin Insulator in Pollution Condition Using Particle Swarm and Neural Network. In Proceedings of the 2017 5th International Conference on Electrical Engineering-Boumerdes (ICEE-B), Boumerdes, Algeria, 29–31 October 2017. [Google Scholar]
- Liu, L. The Influence of Electric Field Distribution on Insulator Surface Flashover. In Proceedings of the 2018 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Cancun, Mexico, 21–24 October 2018. [Google Scholar]
- Yu, X.; Yang, X.; Zhang, Q.; Yu, X.; Zhou, J.; Liu, B. Effect of Booster Shed on Ceramic Post Insulator Pollution Flashover Performance Improvement. In Proceedings of the 2016 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Chengdu, China, 19–22 September 2016. [Google Scholar]
- Jiang, X.; Yuan, J.; Zhang, Z.; Hu, J.; Sun, C. Study on AC Artificial-Contaminated Flashover Performance of Various Types of Insulators. IEEE Trans. Power Deliv. 2007, 22, 2567–2574. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, Z.; Hu, J. Investigation on Flashover Voltage and Non-uniform Pollution Correction Coefficient of DC Composite Insulator. In Proceedings of the 2008 International Conference on High Voltage Engineering and Application, Chongqing, China, 9–12 November 2008. [Google Scholar]
- He, J.; Gorur, R.S. Flashover of Insulators in a Wet Environment. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1038–1044. [Google Scholar] [CrossRef]
- Abd Rahman, M.S.B.; Izadi, M.; Ab Kadir, M.Z.A. Influence of Air Humidity and Contamination on Electrical Field of Polymer Insulator. In Proceedings of the 2014 IEEE International Conference on Power and Energy (PECon), Kuching, Malaysia, 1–3 December 2014. [Google Scholar]
- He, J.; Gorur, R.S. A Probabilistic Model for Insulator Flashover under Contaminated Conditions. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 555–563. [Google Scholar] [CrossRef]
- Pushpa, Y.G.; Vasudev, N. Artificial Pollution Testing of Polymeric Insulators by CIGRE Round Robin Method -Withstand & Flashover Characteristics. In Proceedings of the 3rd International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Chandigarh, India, 16–18 November 2017. [Google Scholar]
- Chan, H.; Fan, C.; Kuo, C. Generalized Finite Difference Method for Solving Two-Dimensional Non-Linear Obstacle Problems. Eng. Anal. Bound. Elem. 2013, 37, 1189–1196. [Google Scholar] [CrossRef]



















| Time Nodes | Simulation (s) | Experiment (s) | Error (%) |
|---|---|---|---|
| Dry band formation | 1.6 | 1.6 | 0 |
| Arc igniting | 5.42 | 5.6 | 3.2 |
| Arc extinction | 5.51 | 5.8 | 5 |
| Arc reigniting | 8.57 | 9.7 | 11.6 |
| Multiple arc occurrences | 9.89 | 10.1 | 2.1 |
| Flashover | 14.64 | 15.4 | 4.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; He, K.; Gao, B. Modeling of Dry Band Formation and Arcing Processes on the Polluted Composite Insulator Surface. Energies 2019, 12, 3905. https://doi.org/10.3390/en12203905
He J, He K, Gao B. Modeling of Dry Band Formation and Arcing Processes on the Polluted Composite Insulator Surface. Energies. 2019; 12(20):3905. https://doi.org/10.3390/en12203905
Chicago/Turabian StyleHe, Jiahong, Kang He, and Bingtuan Gao. 2019. "Modeling of Dry Band Formation and Arcing Processes on the Polluted Composite Insulator Surface" Energies 12, no. 20: 3905. https://doi.org/10.3390/en12203905
APA StyleHe, J., He, K., & Gao, B. (2019). Modeling of Dry Band Formation and Arcing Processes on the Polluted Composite Insulator Surface. Energies, 12(20), 3905. https://doi.org/10.3390/en12203905