Efficient Model Predictive Control with Natural Fault-Tolerance in Asymmetrical Six-Phase Induction Machines

Abstract

Multiphase machines allow enhancing the performance of wind energy conversion systems from the point of view of reliability and efficiency. The enhanced robustness has been traditionally achieved with a mandatory post-fault control reconfiguration. Nevertheless, when the regulation of x-y currents in multiphase drives is done in open-loop mode, the reconfiguration can be avoided. As a consequence, the reliability of the system increases because fault detection errors or delays have no impact on the post-fault performance. This capability has been recently defined as natural fault tolerance. From the point of view of the efficiency, multiphase machines present a better power density than three-phase machines and lower per-phase currents for the same voltage rating. Moreover, the implementation of control strategies based on a variable flux level can further reduce the system losses. Targeting higher reliability and efficiency for multiphase wind energy conversion systems, this work proposes the implementation of an efficient model predictive control using virtual voltage vectors for six-phase induction machines. The use of virtual voltage vectors allows regulation of the x-y currents in open-loop mode and achieving the desired natural fault tolerance. Then, a higher efficiency can be achieved with a simple and universal cost function, which is valid both in pre- and post-fault situations. Experimental results confirm the viability and goodness of the proposal.

1. Introduction

Promoted by new energy policies in different countries, renewable energies currently play an important role in the electricity market [1]. There is a wide variety of clean energies aiming to replace fossil fuels, but wind energy is the most installed one in the world. In fact, a high percentage of the demanded electric energy is obtained nowadays from wind energy conversion systems (WECS). This high penetration of wind energy has, in turn, increased the requirements from transmission system operators to WECS.

In this context, the efficiency and reliability are two desirable features for the newly developed WECSs. Since multiphase machines present enhanced fault-tolerant (FT) capabilities and better power densities than conventional three-phase systems [2,3,4], multiphase generators appear as promising candidates in full-power WECS. The improved post-fault operation capability of multiphase machines can provide economic benefits when the corrective maintenance tasks are complex, as it is the case in offshore locations [5]. Furthermore, the better power density of multiphase machines allows lower copper losses, increasing the wind resource exploitation. Hence, multiphase machines have become an interesting alternative in modern wind farms [6].

In terms of reliability, the FT capability, and particularly the open-phase fault (OPF) operation, can be considered the most appreciated advantage of multiphase machines, but this higher reliability has been traditionally achieved with a mandatory OPF localization/isolation [7] and a post-fault control reconfiguration [8]. Nevertheless, the natural FT recently suggested in [9] circumvents this standard trend of post-fault control strategies and provides simpler means to obtain an improved reliability. The model predictive control (MPC) based on virtual voltage vectors (VV) from [9] provides an enhanced post-fault capability without fault localization and control reconfiguration. The implementation of VVs in MPC allows regulating the x-y currents in open-loop mode. This fact avoids the conflict of the α-β and x-y controllers when a new restriction appears in the system due to the OPF. As a consequence, the VV-MPC becomes a universal control strategy for pre- and post-fault situations, this being a highly attractive feature for the wind energy industry. However, regardless of the selected post-fault strategy, the integrity of the system in post-fault situation can only be preserved by decreasing the torque/power production (derating) [8,10].

Efficiency is also a highly appreciated characteristic of WECS because lower losses imply a better exploitation of the wind energy resources and greater torque/power production in post-fault situations. The concept of efficient control is based on the reduction of the magnetic flux in the machine at light loads to minimize the copper losses. Efficient control has been traditionally implemented using two different strategies: search control (SC) [11,12,13] and loss model control (LMC) [14,15,16] methods. SC algorithms produce an online perturbation in the magnetic flux when looking for the optimal balance between torque and magnetization. Then, the convergence provided by SC methods is slow, although it is insensitive to machine parameters [13]. On the other hand, LMC techniques are based on the theoretical estimation of the magnetic flux using a model of the system [14], arising higher speed convergences and sensitivity to variations in the machine parameters. In order to develop more competitive WECSs, an efficient LMC strategy was successfully implemented in [16] for a six-phase IM in post-fault situation using field-oriented control (FOC). Nevertheless, the developed efficient model was based on a selected topology (with parallel converters) and specific post-fault situations, i.e., this efficient model is only valid for these particular conditions. If the machine is driven with a single VSC supply and the system is healthy, the efficient control must be revisited to achieve a more general strategy that ensures its validity both before and after the OPF occurrence.

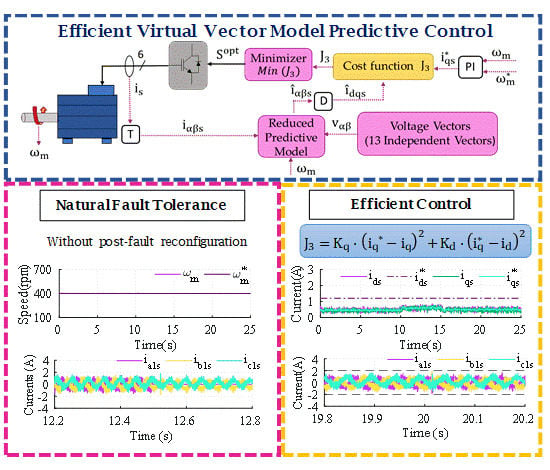
With the aim of providing natural fault tolerance capability and lower losses, an efficient MPC technique based on virtual voltage vectors (EVV-MPC) was suggested in [17]. This work confirmed for the first time the interest of EVV-MPC, improving the efficiency and reliability of six-phase IM drives in pre- and post-fault situations while maintaining the same control scheme. However, the analysis presented in [17] was only supported by simulations. This work goes beyond, providing a detailed analysis and experimental results that confirm the EVV-MPC features in steady or transient states and healthy or post-fault situations and avoiding any sensitivity to parameter detuning when evaluating the optimal magnetic flux level. The paper has been structured as follows: A description of the analyzed multiphase induction machine is included in the next section, and the model predictive control using virtual voltage vectors and the concept of natural fault tolerance are detailed in Section 3. Next, the efficient control scheme presented in this work is detailed in Section 4 and validated through experimentation in Section 5. The obtained conclusions are finally summarized in the last section.

2. Asymmetrical Six-Phase Induction Drives

The studied multiphase drive is formed by an asymmetrical six-phase induction machine with distributed windings where two independent and isolated neutral points are created, supplied by two three-phase and two-level voltage source converters (VSCs) connected to a single DC link (Figure 1). The switching state of every VSC leg can be defined using a binary variable $S_{ij}$, being $S_{ij}=0$ if the lower switch is ON and the upper switch is OFF, and $S_{ij}=1$ if the opposite situation occurs. According to the number of phases of the proposed IM drive, $2^6=64$ switching states exist. It is common to group theses switching states in a vector $\left[S\right]=\left\{S_{a1},S_{b1},S_{c1},S_{a2},S_{b2},S_{c2}\right\}$ that determines the obtained stator phase voltage from the DC-link voltage ($V_{dc}$) as follows:

$$\left[\mathrm{M}\right]=\frac{{\mathrm{V}}_{\mathrm{DC}}}{3}·\left[\begin{array}{cccccc}2& -1& -1& 0& 0& 0\\ -1& 2& -1& 0& 0& 0\\ -1& -1& 2& 0& 0& 0\\ 0& 0& 0& 2& -1& -1\\ 0& 0& 0& -1& 2& -1\\ 0& 0& 0& -1& -1& 2\end{array}\right]·{\left[\mathrm{S}\right]}^{\mathrm{T}},$$

(1)

The current invariant Clarke transformation is usually applied to simplify the mathematical description of the system from phase-variables into two orthogonal stationary subspaces, $\alpha$-$\beta$ and $x$-$y$ (see Figure 2):

$$\begin{gathered} \left[\mathrm{T}\right]=\frac{1}{3}\left[\begin{array}{cccccc}1& -1/2& -1/2& \sqrt{3}/2& -\sqrt{3}/2& 0\\ 0& \sqrt{3}/2& -\sqrt{3}/2& 1/2& 1/2& -1\\ 1& -1/2& -1/2& -\sqrt{3}/2& \sqrt{3}/2& 0\\ 0& -\sqrt{3}/2& \sqrt{3}/2& 1/2& 1/2& -1\\ 1& 1& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 1\end{array}\right], \\ {\left[{\mathrm{v}}_{\mathsf{\alpha }\mathrm{s}}{\mathrm{v}}_{\mathsf{\beta }\mathrm{s}}{\mathrm{v}}_{\mathrm{xs}}{\mathrm{v}}_{\mathrm{ys}}{\mathrm{v}}_{0+}{\mathrm{v}}_{0-}\right]}^{\mathrm{T}}=\left[\mathrm{T}\right]·{\left[{\mathrm{v}}_{\mathrm{a}1}{\mathrm{v}}_{\mathrm{b}1}{\mathrm{v}}_{\mathrm{c}1}{\mathrm{v}}_{\mathrm{a}2}{\mathrm{v}}_{\mathrm{b}2}{\mathrm{v}}_{\mathrm{c}2}\right]}^{\mathrm{T}}, \end{gathered}$$

(2)

where $\alpha$-$\beta$ components are related with the flux/torque generation, $x$-y components produce copper losses, and the isolated neutral points simplify the analysis and avoid triples stator current harmonics. Based on this fact, the vector space decomposition (VSD) approach is usually applied to define the six-phase IM as follows [18]:

$$\begin{gathered} {\mathrm{v}}_{\mathsf{\alpha }\mathrm{s}}=\left({\mathrm{R}}_{\mathrm{s}}{+\mathrm{L}}_{\mathrm{s}}·\frac{\mathrm{d}}{\mathrm{dt}}\right){\mathrm{i}}_{\mathsf{\alpha }\mathrm{s}}+\mathrm{M}·\frac{{\mathrm{di}}_{\mathsf{\alpha }\mathrm{r}}}{\mathrm{dt}}, \\ {\mathrm{v}}_{\mathsf{\beta }\mathrm{s}}=\left({\mathrm{R}}_{\mathrm{s}}{+\mathrm{L}}_{\mathrm{s}}·\frac{\mathrm{d}}{\mathrm{dt}}\right){·\mathrm{i}}_{\mathsf{\beta }\mathrm{s}}+\mathrm{M}·\frac{{\mathrm{di}}_{\mathsf{\beta }\mathrm{r}}}{\mathrm{dt}}, \\ {\mathrm{v}}_{\mathrm{xs}}=\left({\mathrm{R}}_{\mathrm{s}}{+\mathrm{L}}_{\mathrm{ls}}·\frac{\mathrm{d}}{\mathrm{dt}}\right)·{\mathrm{i}}_{\mathrm{xs}}, \\ {\mathrm{v}}_{\mathrm{ys}}=\left({\mathrm{R}}_{\mathrm{s}}{+\mathrm{L}}_{\mathrm{ls}}·\frac{\mathrm{d}}{\mathrm{dt}}\right)·{\mathrm{i}}_{\mathrm{ys}}, \\ 0=\left({\mathrm{R}}_{\mathrm{r}}+\mathrm{Lr}·\frac{\mathrm{d}}{\mathrm{dt}}\right){\mathrm{i}}_{\mathsf{\alpha }\mathrm{r}}+\mathrm{M}·\frac{{\mathrm{di}}_{\mathsf{\alpha }\mathrm{s}}}{\mathrm{dt}}{+\mathsf{\omega }}_{\mathrm{r}}{·\mathrm{L}}_{\mathrm{r}}{·\mathrm{i}}_{\mathsf{\beta }\mathrm{r}}{+\mathsf{\omega }}_{\mathrm{r}}{·\mathrm{M}·\mathrm{i}}_{\mathsf{\beta }\mathrm{s}}, \\ 0=\left({\mathrm{R}}_{\mathrm{r}}+\mathrm{Lr}·\frac{\mathrm{d}}{\mathrm{dt}}\right)·{\mathrm{i}}_{\mathsf{\beta }\mathrm{r}}+\mathrm{M}·\frac{{\mathrm{di}}_{\mathsf{\beta }\mathrm{s}}}{\mathrm{dt}}{-\mathsf{\omega }}_{\mathrm{r}}·{\mathrm{L}}_{\mathrm{r}}·{\mathrm{i}}_{\mathsf{\alpha }\mathrm{r}}{-\mathsf{\omega }}_{\mathrm{r}}{·\mathrm{M}·\mathrm{i}}_{\mathsf{\alpha }\mathrm{s}}, \\ {\mathrm{T}}_{\mathrm{e}}{=\mathrm{p}·\mathrm{M}·(\mathrm{i}}_{\mathsf{\beta }\mathrm{r}}·{\mathrm{i}}_{\mathsf{\alpha }\mathrm{s}}{-\mathrm{i}}_{\mathsf{\alpha }\mathrm{s}}·{\mathrm{i}}_{\mathsf{\beta }\mathrm{s}}), \end{gathered}$$

(3)

where $L_s=L_{ls}+3·L_m$, $L_r=L_{lr}+3·L_m$, $M=3·L_m$,${\omega }_r=p·{\omega }_m$, with $p$ and${\omega }_m$ being the mechanical speed. In addition, indices $\mathrm{s}$ and $r$ denote stator and rotor variables and subscripts $l$ and $m$ denote leakage and magnetizing inductance, respectively.

To simplify the control a synchronous reference frame $(d$-$q$) can be employed where the $d$-component is related with flux production and the $q$- component with the torque production. This transformation of the reference frame is obtained applying the Park transformation in Equation (4) to the $\alpha$-$\beta$ components as follows:

$$\begin{gathered} \left[\mathrm{D}\right]=\left[\begin{array}{cc}\cos \left({\mathsf{\theta }}_{\mathrm{s}}\right)& \sin \left({\mathsf{\theta }}_{\mathrm{s}}\right)\\ -\sin \left({\mathsf{\theta }}_{\mathrm{s}}\right)& \cos \left({\mathsf{\theta }}_{\mathrm{s}}\right)\end{array}\right], \\ {\left[i_{\mathrm{ds}}{i}_{\mathrm{qs}}\right]}^{\mathrm{T}}=\left[\mathrm{D}\right]·{\left[i_{\mathsf{\alpha }\mathrm{s}}{i}_{\mathsf{\beta }\mathrm{s}}\right]}^{\mathrm{T}},{\left[i_{\mathrm{x}1\mathrm{s}}{i}_{\mathrm{y}1\mathrm{s}}\right]}^{\mathrm{T}}=\left[\mathrm{D}\right]·{\left[i_{\mathrm{xs}}{i}_{\mathrm{ys}}\right]}^{\mathrm{T}}, \end{gathered}$$

(4)

with ${\theta }_s$ being the angle of the reference frame, obtained from the measured speed (${\omega }_m$) and the estimated slip [19].

3. VV-MPC with Natural Fault Tolerance

Standard MPC (see Figure 3) uses an outer speed control loop with a PI controller to obtain the reference value of the $q$-current, whereas the $d$-current is usually set to a fixed value that is proportional to the rated flux in the base-speed region. In addition, an inner predictive current controller regulates the power converter that feeds the machine and commands the electromechanical system. This current controller is based on a discretized machine model that is used to predict currents in future operation points [9]. The predicted currents are then included in a predefined cost function (Equation (5)) where different error terms are included and whose final value is minimized to find an optimal switching state:

$${\mathrm{J}}_1{=\mathrm{K}}_1{·\mathrm{e}}_{\mathrm{qs}}^2{+\mathrm{K}}_2{·\mathrm{e}}_{\mathrm{ds}}^2{+\mathrm{K}}_3{·\mathrm{e}}_{\mathrm{xs}}^2{+\mathrm{K}}_4{·\mathrm{e}}_{\mathrm{ys}}^2,$$

(5)

where $K_i$ coefficients, also called weighting factors and defined to achieve regulation goals and drive features, multiply i-error components that are defined in this case as follows:

$$\begin{array}{ll}{\mathrm{e}}_{\mathrm{qs}}{=(\mathrm{i}}_{\mathrm{qs}}^{*}{|}_{\mathrm{k}+2} {-\hat{\mathrm{l}}}_{\mathrm{qs}}{|}_{\mathrm{k}+2}),& {\mathrm{e}}_{\mathrm{xs}}=({\mathrm{i}}_{\mathrm{xs}}^{*}{|}_{\mathrm{k}+2} - {\hat{\mathrm{l}}}_{\mathrm{xs}}{|}_{\mathrm{k}+2}),\\ {\mathrm{e}}_{\mathrm{ds}}{=(\mathrm{i}}_{\mathrm{ds}}^{*}{|}_{\mathrm{k}+2}-{\hat{\mathrm{l}}}_{\mathrm{ds}}{|}_{\mathrm{k}+2}),& {\mathrm{e}}_{\mathrm{ys}}{=(\mathrm{i}}_{\mathrm{ys}}^{*}{|}_{\mathrm{k}+2}-{\hat{\mathrm{l}}}_{\mathrm{ys}}{|}_{\mathrm{k}+2}),\end{array}$$

(6)

being the predicted currents in $k+2$ (“${\hat{\mathrm{l}}}_{\mathrm{qs}}{|}_{\mathrm{k}+2}$”) compared with the reference currents (“${\mathrm{i}}_{\mathrm{qs}}^{*}{|}_{\mathrm{k}+2}$”) in k + 2 to apply the optimal switching state to the power converter.

Note that the reference values of the $x$-$y$ currents are usually set to a null value in order to reduce stator copper losses in distributed-winding machines. However, it was recently stated that its performance can be highly degraded if the stator leakage inductance of the machine presents a low value [19]. The standard MPC technique applies a single switching state during the whole sampling time, generating simultaneously voltage vectors in $\alpha$-$\beta$ and $x$-$y$ planes when active voltage vectors are applied. Consequently, $x$-$y$ currents flow through the machine, spoiling the current quality and increasing the stator copper losses.

To solve the aforementioned disadvantage, [20,21] proposed the implementation of virtual voltage vectors for MPC strategies. The VVs are created taking advantage of the special localization of the available six-phase IM voltage vectors. As shown in Figure 2, voltage vectors can be classified depending on their magnitude in small, medium, medium-large and large voltage vectors where medium-large and large vectors that share their direction in the $\alpha$-$\beta$ plane have opposite directions in the $x$-$y$ plane. Hence, it is possible to obtain a virtual voltage vector as a combination of medium-large and large vectors, providing a null average $x$-$y$ voltage production. For this purpose, it is necessary to apply different times for medium-large and large voltage vectors. In a six-phase VSC, the application time of each vector must be $t_1=0.73·T_m$ (for large voltage vectors) and $t_2=0.27·T_m$ (for medium-large voltage vectors), being $T_m$ the sampling period. Following this approach, 12 active virtual voltage vectors can be defined as:

$${\mathrm{VV}}_{\mathrm{i}}{=\mathrm{t}}_1{·\mathrm{V}}_{\mathrm{large}}{+\mathrm{t}}_2{·\mathrm{V}}_{\mathrm{medium}-\mathrm{large}}$$

(7)

With the application of these VV, the control of $x$-$y$ currents is performed in open-loop mode, with no inclusion of these components into the control strategy. This simplification results in a reduced predictive model that skip the x-y equations [20,21]. Consequently, the number of weighting factors can be reduced compared to standard MPC and the $x$-$y$ term can be eliminated from the cost function as follows:

$${\mathrm{J}}_2{=\mathrm{K}}_1·{\left({\mathrm{i}}_{\mathrm{qs}}^{*}{|}_{\mathrm{k}+2}-{\hat{\mathrm{l}}}_{\mathrm{qs}}{|}_{\mathrm{k}+2}\right)}^2{+\mathrm{K}}_2·{\left({\mathrm{i}}_{\mathrm{ds}}^{*}{|}_{\mathrm{k}+2}-\hat{\mathrm{l}}{|}_{\mathrm{k}+2}\right)}^2,$$

(8)

Figure 4 shows the VV-MPC scheme where the main differences with the standard MPC (Figure 3) have been colored in magenta. Additionally, VVs provide MPC with a natural fault-tolerant characteristic because the regulation of the x-y currents is performed in open-loop mode and the controllers’ conflicts after the fault occurrence are eliminated [9]. Based on this, the post-fault reconfiguration can be suppressed, and the reliability of the entire system is improved thanks to a reduced impact of the fault detection errors or delays on the post-fault operation and performance.

This natural fault tolerance concept has introduced a new paradigm in the field of fault-tolerant multiphase drives, where a mandatory post-fault reconfiguration of the healthy control scheme has been historically used in the event of an OPF [22,23,24,25]. Conventional post-fault strategies reconfigure the control scheme according to the fault localization in order to avoid the controllers’ conflicts. Since the fault situation is missed and the control action is not modified, the drive performance can be distorted because $\alpha$-$\beta$ and $x$-$y$ subspaces are no longer independent and the controllers usually have conflicting objectives. If a single OPF in phase $a_1$ occurs in the analyzed system, the new restriction is [8]:

$${\mathrm{i}}_{\mathrm{xs}}{=-\mathrm{i}}_{\mathsf{\alpha }\mathrm{s}}$$

(9)

This restriction does not allow the independent regulation of stator currents in the primary and secondary planes, forcing a conflict if healthy controllers are applied in post-fault operation. In order to avoid any conflict and preserve the controllability of the system in post-fault operation, $x$-$y$ reference currents have been traditionally modified in order to drive $\alpha$-$\beta$ and $x$-$y$ controllers into a single direction (with $i_{xs}^{*}=-i_{\alpha s}^{*}$ [8]). However, if the $x$-$y$ currents are regulated in the open-loop mode, the conflict is automatically avoided because the $x$-$y$ terms are not included in the cost function [9]. Nevertheless, and regardless of the selected post-fault strategy, the machine must be derated in order to safeguard the integrity of the system. This fact could promote the selection of efficient strategies where the magnetic flux level is variated at light loads to reduce the stator copper losses.

4. Efficient Model Predictive Control Based on Virtual Voltage Vectors

From the efficiency point of view, the most widely selected approach is to adapt the flux to reduce the stator copper losses. Focusing on these losses, they can be expressed as the product of stator resistance and the squared RMS (Root Mean Square) value of phase currents:

$${\mathrm{P}}_{\mathrm{cu}}{=6·\mathrm{R}}_{\mathrm{s}}{·\mathrm{i}}_{\mathrm{s}}^2,.$$

(10)

On the other hand, according to the VSD approach and considering the Park transformation, the RMS value of the phase currents can be calculated as:

$${\mathrm{i}}_{\mathrm{s}}=\sqrt{{\mathrm{i}}_{\mathrm{ds}}^2{+\mathrm{i}}_{\mathrm{qs}}^2{+\mathrm{i}}_{\mathrm{xs}}^2{+\mathrm{i}}_{\mathrm{ys}}^2},$$

(11)

Trefore, to obtain the minimum stator copper losses, Equation (11) must be minimized. Efficient strategies are based on the magnetic flux variation according to the operating point with the aim of minimizing stator copper losses. The operation point of an induction machine can be usually defined by the magnetic flux level and the required electromagnetic torque, being expressed the electromagnetic torque in IMs with distributed windings using $d$-$q$ currents as follows:

$${\mathrm{T}}_{\mathrm{e}}=\frac{{\mathrm{P}·\mathrm{L}}_{\mathrm{m}}^2}{{\mathrm{L}}_{\mathrm{r}}}{·\mathrm{i}}_{\mathrm{ds}}{·\mathrm{i}}_{\mathrm{qs}},$$

(12)

Based on Equations (10)–(12), a constrained minimization problem can be formulated in order to obtain the minimum RMS value of the phase currents for each operation point as:

$$\begin{gathered} {\mathrm{Minimize}:\mathrm{i}}_{\mathrm{ds}}^2{+\mathrm{i}}_{\mathrm{qs}}^2{+\mathrm{i}}_{\mathrm{xs}}^2{+\mathrm{i}}_{\mathrm{ys}}^2, \\ {\mathrm{subject}\mathrm{to}:\mathrm{T}}_{\mathrm{e}}=\frac{{\mathrm{P}·\mathrm{L}}_{\mathrm{m}}^2}{{\mathrm{L}}_{\mathrm{r}}}{·\mathrm{i}}_{\mathrm{ds}}{·\mathrm{i}}_{\mathrm{qs}}, \end{gathered}$$

(13)

Although there are different solvers, the Lagrange function solves this constrained minimization problem in a straightforward manner as follows:

$$\mathrm{L}\left({\mathrm{i}}_{\mathrm{ds}}{,\mathrm{i}}_{\mathrm{qs}}{,\mathrm{i}}_{\mathrm{xs}}{,\mathrm{i}}_{\mathrm{ys}},\mathsf{\lambda }\right){=\mathrm{i}}_{\mathrm{ds}}^2{+\mathrm{i}}_{\mathrm{qs}}^2{+\mathrm{i}}_{\mathrm{xs}}^2{+\mathrm{i}}_{\mathrm{ys}}^2{+\mathsf{\lambda }·\mathrm{T}}_{\mathrm{e}}-\frac{{\mathsf{\lambda }·\mathrm{P}·\mathrm{L}}_{\mathrm{m}}^2}{{\mathrm{L}}_{\mathrm{r}}}{·\mathrm{i}}_{\mathrm{ds}}{·\mathrm{i}}_{\mathrm{qs}},$$

(14)

where $\mathsf{\lambda }$ is the Lagrange multiplier.

Implementing each minimization condition:

$$\begin{gathered} \frac{\partial \mathrm{L}}{\partial {\mathrm{i}}_{\mathrm{ds}}}{=2·\mathrm{i}}_{\mathrm{ds}}-\mathsf{\lambda }·\frac{{\mathrm{P}·\mathrm{L}}_{\mathrm{m}}^2}{{\mathrm{L}}_{\mathrm{r}}}{·\mathrm{i}}_{\mathrm{qs}}=0, \\ \frac{\partial \mathrm{L}}{\partial {\mathrm{i}}_{\mathrm{qs}}}{=2·\mathrm{i}}_{\mathrm{qs}}-\mathsf{\lambda }·\frac{{\mathrm{P}·\mathrm{L}}_{\mathrm{m}}^2}{{\mathrm{L}}_{\mathrm{r}}}{·\mathrm{i}}_{\mathrm{ds}}=0, \\ \frac{\partial \mathrm{L}}{\partial {\mathrm{i}}_{\mathrm{xs}}}{=2·\mathrm{i}}_{\mathrm{xs}}=0, \\ \frac{\partial \mathrm{L}}{\partial {\mathrm{i}}_{\mathrm{ys}}}{=2·\mathrm{i}}_{\mathrm{ys}}=0, \\ \frac{\partial \mathrm{L}}{\partial \mathsf{\lambda }}{=\mathrm{T}}_{\mathrm{e}}-\frac{{\mathrm{P}·\mathrm{L}}_{\mathrm{m}}^2}{{\mathrm{L}}_{\mathrm{r}}}{·\mathrm{i}}_{\mathrm{ds}}{·\mathrm{i}}_{\mathrm{qs}} \end{gathered}$$

(15)

The reference value of the $d$-current that provides minimum stator current RMS value for a given load torque can be obtained from Equation (15) as:

$${\mathrm{i}}_{\mathrm{ds}}=\sqrt{\frac{{\mathrm{Te}·\mathrm{L}}_{\mathrm{r}}}{{\mathrm{P}·\mathrm{L}}_{\mathrm{m}}^2}},$$

(16)

Note that Equation (15) also provides the value of $q$ and $x$-$y$ currents that achieve the minimum RMS value of phase currents for the corresponding electromagnetic torque. Even though $x$-$y$ currents appear as a component in the calculation of stator phase current RMS values, they are not included in torque restriction equation, and do not affect the optimization problem, presenting a zero value as a solution. This fact has special relevance in faulty operation, where the $x$-$y$ components have a non-null value due to the OPF constraint: since the maximum efficiency does not depend on the $x$-$y$ currents, it is not necessary to modify the control scheme after the OPF occurrence and the control algorithm can maintain the efficiency in pre- and post-fault scenarios. On the other hand, $i_{qs}$ can be obtained from the constrained minimization problem as:

$${\mathrm{i}}_{\mathrm{qs}}=\sqrt{\frac{{\mathrm{Te}·\mathrm{L}}_{\mathrm{r}}}{{\mathrm{P}·\mathrm{L}}_{\mathrm{m}}^2}},$$

(17)

From a mathematical point of view, Equations (16) and (17) are identical, which means that it is possible to implement an efficient control scheme replacing the $d$-current rated value with the actual reference value of the $q$-current:

$${\mathrm{i}}_{\mathrm{ds}}{}^{*}{=\mathrm{i}}_{\mathrm{qs}}{}^{*},$$

(18)

However, this approach is not achievable if the electromagnetic torque imposed by the operating point is higher than a critical value (Equation (19)), since an overrated $d$-current leads to magnetic saturation and distorts the control performance.

$${\mathrm{T}}_{\mathrm{e}}^{\mathrm{critical}}=\mathrm{P}·\frac{{\mathrm{L}}_{\mathrm{m}}^2}{{\mathrm{L}}_{\mathrm{r}}}{·\mathrm{id}}_{\mathrm{s}}^{\mathrm{rated}}{·\mathrm{id}}_{\mathrm{s}}^{\mathrm{rated}}$$

(19)

The efficient strategy is implemented in VV-MPC with a new cost function (Equation (20)) that allows the electromagnetic torque production control (first term) and the magnetic flux adaptation to the corresponding operation point (second term). The method can be used when the system is operated with light load torques, which matches the specific derated condition in the post-fault situation to safeguard the integrity of the system.

$${\mathrm{J}}_3{=\mathrm{K}}_1·{\left({\mathrm{i}}_{\mathrm{qs}}^{*}{|}_{\mathrm{k}+2}-{\hat{\mathrm{l}}}_{\mathrm{qs}}{|}_{\mathrm{k}+2}\right)}^2{+\mathrm{K}}_2·{\left({\mathrm{i}}_{\mathrm{qs}}^{*}{|}_{\mathrm{k}+2}-{\hat{\mathrm{l}}}_{\mathrm{ds}}{|}_{\mathrm{k}+2}\right)}^2,$$

(20)

In summary, this new cost function does not only improve the efficiency of the system, but also maintains its natural fault-tolerant capability due to the open-loop regulation of $x$-$y$ currents. Moreover, the introduced efficient cost function is also universal, being valid in pre- and post- fault situations and avoiding any control reconfiguration. Figure 5 shows the proposed EVV-MPC, where the introduced cost function is highlighted in yellow.

5. Viability of the Proposal

The viability and goodness of the proposal is analyzed using the test bench shown in Figure 6, where the asymmetrical six-phase IM is fed by conventional two-level three-phase VSC (Semikron SKS22F modules (Semikron, Nuremberg, Germany)). The parameters of the custom-built six-phase IM have been obtained using ac-time domain and stand-still with inverter supply tests [26,27].

Table 1. Electric drive parameters.

Power (kW)	0.8
Dc-link voltage(V)	300
Dead time ($\mathsf{\mu }s$)	4
${\mathrm{I}}_{\mathrm{peak}}\left(\mathrm{A}\right)$	4.06
${\mathrm{n}}_{\mathrm{m}}(\mathrm{r}/\min )$	1000
${\mathrm{R}}_{\mathrm{s}}\left(\mathsf{\Omega }\right)$	4.2
${\mathrm{R}}_{\mathrm{r}}\left(\mathsf{\Omega }\right)$	2
${\mathrm{L}}_{\mathrm{m}}\left(\mathrm{mH}\right)$	420
${\mathrm{L}}_{\mathrm{ls}}\left(\mathrm{mH}\right)$	1.5
${\mathrm{L}}_{\mathrm{lr}}\left(\mathrm{mH}\right)$	55

shows the main parameters of the electric driver where the value of the stator resistance and leakage inductance of the $\alpha$-$\beta$ and $x$-$y$ planes are the same.

A single DC power supplies the VSC and the control actions are performed by a digital signal processor (TMS320F28335 from Texas Instruments, TI (Texas Instruments, Dallas, TX, USA)). The current and speed measurements are obtained using four hall-effect sensors (LEM LAH 25-NP (LEM, Bourg-la-Reine, France)) and a digital encoder (GHM510296R/2500 (Sensata, Attleboro, MA, USA)), respectively, while the six-phase IM is loaded by a coupled DC machine. Note that the armature of the DC machine is connected to a variable passive R load that dissipates the power and the load torque is consequently speed-dependent. Note also that the open-phase fault is forced from the TMS320F28335 using a controllable relay board between the inverter and the machine. Then, the performance of the proposed EVV-MPC can be assessed in pre- and post-fault situations, where four different tests have been designed.

A speed ramp test is firstly realized in pre-fault situation (see Figure 7) to evaluate the performance of the proposed controller (right column). The reference speed is changed from 200 to 400 rpm, and a VV-MPC strategy is also tested for comparison purposes using the same operation conditions (left column). The tracking of the reference speed is satisfactory regardless of the selected control strategy (see left and right columns, Figure 7a). However, the $d$-current in VV-MPC is constant all throughout the test (left column, Figure 7b), whereas in the case of EVV-MPC it follows the $q$-current reference according to the cost function detailed in Equation (20) (right column, Figure 7b). The difference between the reference of the $q$-current and the measured $d$-current is depicted in Figure 7c for both control strategies. As previously expressed in Section 4, a null difference reduces the RMS value of the phase currents, as it is shown in Figure 7e,f. Focusing on this issue, EVV-MPC presents an RMS phase current value of 0.57 A compared to 0.92 A in VV-MPC when the speed is low. This difference implies a reduction of 61.61% in the stator copper losses. When high-speed operation is reached, the RMS phase current value is 1.00 A using VV-MPC, whereas 0.60 A is obtained using EVV-MPC. A reduction of copper losses is clearly achieved using variable magnetic flux levels according to the operating point (see Figure 7g), since $x$-$y$ currents have the same behavior using both control strategies in healthy situation (see Figure 7d). Based on these results in healthy operation, it can be confirmed the capability of the proposed EVV-MPC technique to reduce the copper losses for a similar switching frequency than VV-MPC as shown in

Table 2. Switching frequency in pre-fault situation.

Speed	EVV-MPC	VV-MPC
200 rpm	4281 Hz	4296 Hz
400 rpm	4190 Hz	3925 Hz

.

A second test is conducted (see Figure 8) to justify the utilization of the proposed EVV-MPC technique (right column) in the post-fault situation. In this case, the performance in the transition from the pre- to post-fault situation is studied, and the VV-MPC technique is also evaluated (see left column) for the sake of comparison. The system is in healthy operation, but an open-phase fault in phase $a_1$ is forced at $t$=$12.5$s (Figure 8d). The current cannot flow through the open phase and a new restriction appears in the system ($i_x$= −$i_{\alpha }$) as it can be appreciated in Figure 8d,e. Note that the reference speed is satisfactorily tracked using the proposal without any control reconfiguration (see Figure 8a), since $x$-$y$ currents are regulated in open-loop mode and any controller’ conflict exists in post-fault situation. These results validate in fact the natural fault tolerance of MPC strategies when the regulation of $x$-$y$ currents is realized in open-loop mode. On the other hand, the implemented cost function allows adapting the magnetic flux level in pre- and post-fault scenarios without any control reconfiguration, as expected. In this case, $d$-$q$ currents maintain their reference values constant during the whole test (Figure 8b), since the operation point is constant. While the magnetic flux tracks the reference value in VV-MPC, a reduced magnetic level is applied in the case of EVV-MPC (Figure 8f) in order to lessen the stator copper losses. Focusing on the obtained phase currents, EVV-MPC strategy needs a lower value of the phase currents in pre- and post-fault situations to reach the same operation point than using VV-MPC. However, in the post-fault situation the reduction of the $\alpha$-current also provokes a reduction of the $x$-current component since the $\alpha$-$\beta$ and $x$-$y$ planes are no longer independent in faulty operation. Therefore, the implementation of the EVV-MPC strategy provides in the post-fault situation a reduction in the obtained copper losses due to the adaptation of the magnetic flux level. In order to quantify this efficiency improvement,

Table 3. Relative reduction of the RMS phase current value and stator copper losses (SCL) of the healthy phase currents for VV-MPC and EVV-MPC in test 2.

Phase	%RMSpre-fault	%RMSpost-fault	%SCLpre-fault	%SCLpost-fault
${\mathrm{b}}_1$	41.23%	38.99%	65.44%	62.78%
${\mathrm{c}}_1$	40.93%	39.02%	65.10%	62.81%
${\mathrm{a}}_2$	40.40%	42.53%	64.48%	66.97%
${\mathrm{b}}_2$	40.93%	42.96%	65.10%	67.46%
${\mathrm{c}}_2$	39.40%	37.21%	63.28%	60.57%

shows the relative reduction of RMS phase current values and the square of RMS phase current. This second term is related to the stator copper losses associated to theses currents in this test according to Equation (20), where the stator copper losses (SCL) can be obtained independently from the value of the stator resistance $R_s$ as long as the stator resistances are equal in both tests. The obtained results confirm the goodness of the proposed controller in post-fault situation and validate the universality of the implemented cost-function in the pre- and post-fault situations.

$$SCL (\%)=\frac{P_{s\_VV}-P_{s\_EVV}}{P_{s\_VV}}·100=\frac{6·R_s·i_{phase\_VV}^2-6·R_s·i_{phase\_EVV}^2}{6·R_s·i_{phase\_VV}^2}·100=\frac{i_{phase\_VV}^2-i_{phase\_EVV}^2}{i_{phase\_VV}^2}·100$$

(21)

The response of the proposed control scheme is finally evaluated in dynamic post-fault situations (see Figure 9). In this case, the VV-MPC method (left column) is again compared with the proposed EVV-MPC technique (right column), and an open-phase fault is forced in phase $a_1$ at the beginning of the test, appearing a new restriction in the system (Figure 9e,g). The speed is varied in a ramp-wise manner from 200 rpm to 400 rpm (see Figure 9a), being satisfactory the speed regulation in VV-MPC (left column) and EVV-MPC (right column). However, $d$-current changes to adapt its value to each operation point using the proposed EVV-MPC technique, adjusting also the magnetic flux level in dynamic post-fault situations. Meanwhile, the $d$-current value remains constant using VV-MPC during the whole test (Figure 9b), which only adjusts the $q$-current according to the operating point. Flux adaptation provides a reduction of $\alpha$-$\beta$ current amplitudes that are directly related, through inverse Clark transformation, with phase current amplitudes (Figure 9c,d). At low speed operating points, an RMS phase current value of 0.63 A is obtained using EVV-MPC versus 1.10 A with the VV-MPC technique, which implies a reduction of 67.20% of the stator copper losses. When high speed operating points are considered, an RMS phase value of 0.69 A is reached with EVV-MPC against 1.12 A using VV-MPC, which again implies an important reduction of stator copper losses (62.05% in the latter case). This test certifies the interest of the proposed control method that assures speed tracking and improves the efficiency in healthy and faulty operations, and in steady-state and transient conditions without introducing modifications in the control scheme.

A speed reversal test has been realized in pre-fault (left plots in Figure 10) and post-fault (right plots in Figure 10) situations when an open-phase fault occurs in phase $a_1$at $t$=$0 s$. It is shown in both cases that the speed and current tracking is satisfactory (Figure 10a,b), maintaining the efficient control both in healthy mode and in post-fault condition (Figure 10c). The $x$-$y$ currents are regulated around zero in the pre-fault situation (Figure 10d, left column) and show the value ${\mathrm{i}}_{\mathrm{xs}}{=-\mathrm{i}}_{\mathsf{\alpha }\mathrm{s}}$ that corresponds to the post-fault situation (Figure 10d, right column). As expected, phase currents change the sequence after the zero crossing (Figure 10e,f).

6. Conclusions

Efficiency and robustness are a must in industrial electric drives. Even though multiphase machines offer these two features, they are typically achieved at the expense of a high complexity. While the efficiency can be improved using either search control or loss model control, the fault-tolerant operation has been traditionally accomplished with a post-fault control reconfiguration. This work presents a simpler approach that reduces the system losses and increases the drive reliability. The approach is based on the MPC technique, the virtual voltage vector concept and a modified cost function that provides the capability to automatically operate in pre- and post-fault scenarios with excellent speed tracking and reduced copper losses. Key features of the proposal are the simplicity and universality. After a fault occurrence, the proposed strategy keeps on regulating the speed at optimum efficiency even when the fault has not even been detected, making the controller immune to fault detection delays and errors. Although the proposal has been experimentally tested in six-phase IM motor drives, it can be extended to multiphase drives with a higher number of phases if distributed windings are considered.