Interaction of Liquid Droplets in Gas and Vapor Flows

Abstract

We investigated the conditions, characteristics, and outcomes of liquid droplet interaction in the gas medium using video frame processing. The frequency of different droplet collision outcomes and their characteristics were determined. Four interaction regimes were identified: bounce, separation, coalescence, and disruption. Collision regime maps were drawn up using the Weber, Reynolds, Ohnesorge, Laplace, and capillary numbers, as well as dimensionless linear and angular parameters of interaction. Significant differences were established between interaction maps under ideal conditions (two droplets colliding without a possible impact of the neighboring ones) and collision of droplets as aerosol elements. It was shown that the Weber number could not be the only criterion for changing the collision mode, and sizes and concentration of droplets in aerosols influence collision modes. It was established that collisions of droplets in a gaseous medium could lead to an increase in the liquid surface area by 1.5–5 times. Such a large-scale change in the surface area of the liquid significantly intensifies heat transfer and phase transformations in energy systems.

1. Introduction

Over the recent years, optical techniques, cross-correlation systems, high-speed photo, and video recording have made it possible to obtain unique experimental results and extend the concepts of the physics of hydra-dynamic and thermal processes in the area of a large group of gas-droplet systems [1,2,3,4]. Non-contact optical methods are of special note here. These include particle image velocimetry (PIV) [5,6], particle tracking velocimetry (PTV) [7,8], stereo particle image Velocimetry (Stereo PIV) [9,10], interferometric particle imaging (IPI) [11,12] and shadow photography (SP) [13,14]. A major objective of analyzing the gas-vapor-droplet flows [15,16,17,18] is to monitor the component composition, as well as the concentration of droplets, particles, bubbles, vapors, and other components and elements under different heat exchange conditions. The results of experimental research emphasized in the review paper [19] have shown that droplet coalescence is one of the factors determining the component concentration. Typical mechanisms of coalescence and the main patterns of the process were identified in [19]. Droplet coalescence is also crucial for high-temperature (above 1000 °C) gas-vapor-droplet flows due to heat exchange intensification [20,21]. Based on the video frames of the experiments in [22] and the obtained velocity fields of droplets and high-temperature gases, using PIV, Stereo PIV, and PTV, we have formulated a hypothesis that the droplets moving first significantly alter the heat exchange conditions of all the subsequent droplets with gases. The front droplets affect the velocity and evaporation of the following ones, and this depends on droplet dimensions and distances between them. A similar assumption was made from the numerical simulation results [22] of a consecutive motion of several droplets through high-temperature (800–1000 °C) gases (based on the analysis of temperature fields and distribution of gas and vapor concentration around the droplets and in their traces). The experiments in [22] have established the droplet dimensions, their concentrations in the gas medium (or distances between them), and temperatures, for which these effects can be decisive or have quite a significant influence. Of special interest are the identified coalescence effects of droplets consecutively moving through high-temperature (over 800 °C) gases [22,23].

It is most typical of the said applications to use mixed aerosol and gas flows. Phase transformations complicate the task of predicting the characteristics of mixing [24]. They are especially rapid at high temperatures of over 1000 °C and with small droplets. However, experimental research findings are still scarce for the corresponding processes at such temperatures. Consequently, there is quite a limited group of heat and mass transfer models (which were analyzed in [22]) to study these processes and threshold conditions of their realization. With these models, however, it is difficult to study the vaporization or motion of a group of droplets. Therefore, experimental research was conducted in [22] into the influence of the droplet concentration on the conditions of their motion in a high-temperature gas flow, using original techniques and approaches to study these processes with a satisfactory degree of confidence (as illustrated by aerosol [20,21], single liquid droplets or a small group of them [25,26,27,28,29,30,31]). The development of these methods is particularly important in the aspect of conditions corresponding to resource-efficient fuel technologies, thermal treatment, and gas-vapor-droplet heat carriers. The analysis of experimental and theoretical research into the processes of interaction between droplets of different liquids, solutions, emulsions, and slurries when they collide in the gas media [32,33,34,35] shows that the most popular approach to the study of these processes is to record collisions of two droplets in ideal conditions. Consequently, such conditions are assumed in numerical simulation and development of the corresponding models. It appears interesting to study the processes of droplet collisions in aerosols and compare them with the data in [32,33,34,35].

The aim of this research paper is to experimentally determine the main characteristics of interaction between liquid droplets in aerosols under the conditions corresponding to the promising gas-vapor-droplet technologies.

2. Experimental Approach

2.1. Experimental Setup and Methods

We used a setup (Figure 1) supplemented with capillaries and spraying nozzles. The capillaries (14 in Figure 1) were thin hollow needles with an inner diameter of 0.2–0.8 mm. They generated droplets with R_d = 0.5–1 mm. The air compressors (15 in Figure 1), connected to the capillaries with thin tubes filled with liquid, squeezed the droplets out. The spraying nozzles (11 in Figure 1) were pneumatic FE512 sprayers with a full cone pattern. The cone opening angle was 15°, and the liquid flow rate was 0.6–40 mL/s per nozzle at a liquid pressure of 1–4 bars and an atmospheric pressure of 2–5 bars. The nozzles had two outlets: the first one was used for water from reservoir 10, and the second one for air from the air compressor (Figure 1). The generated droplet size varied within the range of R_d = 0.01–0.5 mm.

The objective of this research was to study the conditions of droplet interaction using two spraying nozzles. The capillaries, in this case, were used to obtain additional results to compare them with the data from [20,21]. The experiments investigated various arrangements of droplet generating units (opposite each other, co-directional, and cross-sectional). Considering all the droplet generating units used in the experiments, the variable parameters were in the following ranges: droplet radius R_d = 0.01–1 mm; droplet velocity U_d = 0.1–10 m/s; droplet impact angle α_d = 0°–90°; the relative concentration of aerosol droplets γ_d = 1–3 L/m³.

The droplets were generated from water without any impurities and a slurry containing graphite particles with a mass fraction of 5% (40–50 µm). The solutions were supplied from reservoir 10 (Figure 1) to the spraying nozzles for droplet generation. The graphite slurry was continuously mixed in the reservoir to prevent the solid fraction from settling.

The fine aerosol droplets or individual water droplets were supplied to quartz glass cylinder 13 (Figure 1) to continue their movement within a gas flow. In our experiments, we used a gas flow of two types: heated air flow and combustion products flow (as in [20,21]). System 5 (Figure 1) was used to generate the hot air flow. The system consisted of a LEISTER CH 6060 compressor (Leister Group, Kaegiswil, Switzerland) with a flow rate of 0–5 m/s and a LEISTER LE 5000 HT air heater (Leister Group, Kaegiswil, Switzerland) with a maximum temperature of 900 °C. The flow was then supplied to quartz glass cylinder 13 (Figure 1) through duct 8. Metal cylinder 6 filled with TC-1 grade kerosene was used to generate the combustion products flow. The kerosene was ignited in reservoir 6, and the flue gases went into supply duct 7. Sliding valve 9 (Figure 1) was used to select the gas flow type. Three fast-response type K thermocouples were used to measure the temperature (temperature range 0–1200 °C, accuracy ±1 °C, response time 0.1 s). They were located in the lower, middle, and upper parts of the quartz glass cylinder 13 close to its vertical symmetry axis.

Two high-speed video cameras 1 (Figure 1) were used with the focus in one observation area to obtain 3D presentations of colliding droplets and increase the number of droplet interactions recorded in each experiment: Photron FASTCAM SA 1.1 CMOS video camera (Photron Inc., San Diego, CA, USA) (monochrome sensor; 1024 × 1024 pix resolution; filming rate up to 6.75 × 10⁵ fps; 8 bit depth), Photron FASTCAM Mini UX100 M3 CMOS video camera (Photron Inc., San Diego, CA, USA) (monochrome sensor; 1280 × 1024 pix resolution; filming rate up to 8 × 10⁵ fps; 8 bit depth). We used a Navitar macro lens to record the R_d = 0.01–0.5 mm aerosol flow and a Nikon Micro-Nikkor 200 mm f/4D ED-IF A micro-lens to record the R_d = 0.5–1 mm individual droplets. The frame rate for all the experiments was 3600 fps. The systematic error of time estimate was 3600 fps. Light system 12 (Figure 1) for all the experiments featured 20 W LED spotlights with a 4500 Lm luminous flux. To make the light more even (to avoid a strong luminosity gradient in the video), a matte 1.5 mm thick polycarbonate glass plate was placed between the spotlight and the droplet flux under study. The main task of using two cameras in obtaining 3D images was to study the conditions under which it was enough to use one video camera. Such preliminary experiments were carried out. The minimum values of the depth of field of the lens, the size of the recording area, the concentration of droplets, their initial sizes, and other parameters were established, at which the use of a single camera is sufficient. The frequency of collisions and the recorded frequencies of the collision modes when using 2D and 3D registration differed no more than by 10%. The rest of the article presents the results for such conditions.

Rheological measurements for the compositions were carried out using a Brookfield DV3T LV viscometer (Brookfield AMETEK, New York, NY, USA) at room temperature (20–23 °C). The standard set of the viscometer includes 4 spindles for measuring different viscosity liquids (µ = 0.001–6000 Pa·s); the spindle rotation speed varied from 10 to 250 rpm [36]. The measurement error of the installation in accordance with GOST R 53708-2009 [37] (analog of ASTM D445) was ±1%.

The surface tension of liquids was measured by the ring detachment method (du Nouymethod) [38] using a KRUSS K6 tensimeter (KRÜSS GmbH, Hamburg, Germany) at a temperature of 20 °C. The device was calibrated by measuring the surface tension of double-distilled water (correction factor is 0.995).

The Mathematica and Matlab software bundles were used to perform a preliminary analysis of the video fragments obtained. They were used to capture droplet collisions and to measure droplet radii. With the help of this procedure, we screened 200–400 frames out of 10–20 thousand. The analysis was performed in four stages:

(i) The images were binarized with a fixed threshold to identify the droplets within the focal depth of the optical system used. The binarization threshold was set for each video individually. It was calculated as an arithmetic mean of the brightness for all the droplets with a discernible outline. The algorithm also performed a preliminary screening of all the droplets with a smooth change in the intensity from the edge to the center. This way, we excluded the droplets in which size could be significantly reduced by the binarization as compared to the actual size. All the fragments below the set threshold were identified as a droplet (they were assigned the relative brightness value of 1). All the other objects in the video recording area were considered to be background (they were assigned the relative brightness value of 0). For example, the resolution of video cameras, equal to 8 bit, corresponded to 256 counts. In this case, background image fluctuations were 175–220 counts. These values corresponded to the noise threshold. Drops located beyond the depth of field of the lens corresponded to intensity values of 90–125 counts. The drops that fell into focus had an average intensity of 35–70 counts. Thus, setting the binarization threshold at 70 counts, we were able to eliminate noises and drops that did not fall into focus without using special noise reduction methods.

(ii) For each identified droplet, its motion pattern was plotted, which was generally a straight line. After that, we singled out the frames with intersecting patterns. It should be clarified that in processing the results, the authors used the tracking algorithms of the Tema Automotive software. The x, y coordinates were determined for each identified drop on each frame. After analyzing the sequence of frames at certain coordinates, the trajectory of motion was restored.

(iii) We analyzed the motion patterns and velocities of droplets after their collision. If the direction and velocity remained the same after the collision, the case was excluded. If the droplets changed their direction/velocity or if the droplets coalesced and only one droplet and its motion pattern could be identified after the collision, the cases were processed and analyzed.

(iv) The R_d was determined for the above cases of droplet collision. The previously binarized images of each droplet under study were analyzed to calculate the droplet area S_m(pix) (amount of pixels with the relative brightness of 1), which corresponded to the droplet midsection area. Using the scaling coefficient (s, mm/pix), we converted the values to absolute units: S_m = S_m(pix)∙s². During the experiments, we used several different lenses for the video camera. The focal length was ranged from 100 mm to 200 mm. The values of the scaling coefficient were varied in the range of s = 0.007–0.05 mm/pix. The droplet was assumed to be spherical, so the R_d was calculated by the formula R_d = (S_m/π)^0.5. This algorithm was used to calculate the R_d values for both the pre-collision droplets and the newly formed droplets. The systematic error of the R_d calculation was conditioned by the s value (depending on the recording area) and amounted to 0.003 mm for the aerosol flow and 0.01 mm for large individual droplets.

Photron FastCam software was used to process the obtained video frames. The real shape (sphere or ellipsoid), velocity (U_d), and impact angle (α_d) of each droplet were calculated using the standard functions of the software mentioned before. The algorithms of determining the velocities and dimensions of droplets after their coalescence are similar to the above. The systematic error of α_d recording did not exceed 0.3°. The systematic error of U_d recording did not exceed 0.011 m/s.

Using the Photron FastCam software, the droplet speed was determined by the measured distance (l) and its time of movement (t). The systematic error in estimating the movement speed was determined using the following formula:

δU_d = ±(│(∂U_d/∂l)∙δl│ + │(∂U_d/∂t)∙δt│).

The systematic error δl numerically corresponded to the scaling coefficient (s); the error δt was inversely proportional to the frequency of the video camera. The value of αd was calculated as the angle between two intersecting segments coinciding with the trajectories of the droplets. Each segment was constructed between the positions of the droplet at the initial (before the collision) and final (at the moment of the collision) time points. The length of each segment (r) was at least 200 pix. The error in determining the coordinates of the segment can be 1 pix. The arc length (l) corresponding to the error α_d is also 1 pix, which in terms of degrees will be δα_d = L∙180/(π∙r) = 1 × 180/(3.14 × 200) ≈ 0.3°.

A system based on the Actual Flow software with a group of optical techniques (PIV, IPI, SP), described below, was used to process video frames with approaching droplets and gases.

We used particle image velocimetry (PIV) (as well as in [20,21]) to measure the velocities of water droplets U_d and air flow U_g. The PIV technique is required to estimate the average velocities of gaseous and droplet media. For that, we performed two independent series of experiments before the main research. The first series was to estimate the gas flow velocity U_g and the second one for the aerosol flow velocity U_d. The methods used, as well as the equipment and its settings, remained the same. There was only one difference. The tracing particles for the U_g calculation were the 80–100 nm titanium dioxide (TiO₂) particles injected into the air flow in the lower part of the quartz glass cylinder. The U_d was calculated using water droplets as tracing particles. A Quantel EverGreen 70 dual pulsed laser (Lumibird, Lannion, France) was used to light the recording area (Figure 1). The laser was configured as follows: wavelength 532 nm; maximum pulse energy 35 mJ; pulse frequency 4 Hz; delay in the pair between pulses 150 µs. An optical collimator was used to transform a laser beam into a planar light sheet. The light sheet scanned the air flow vertically along the central symmetry axis of the quartz cylinder. The opening angle of the light sheet was 22°, while its thickness in the measurement region was approx. 0.2 mm. An ImperX IGV-B2020M video camera (Imperx Inc., Boca Raton, FL, USA) (2048 × 2048 pix frame resolution; 8 bit depth) was used to record the tracing particles that entered the light sheet plane. We used a Sigma DG 105 mm f/2.8 EX Macro lens (Sigma Corporation of America, New York, NY, USA) (focal ratio was f/5.6 for U_g measurement and f/16 for U_d measurement). The recording area was 100 × 100 mm. Each experiment involved 300 images. A cross-correlation algorithm of image processing was used for the analysis of the data obtained. Instantaneous velocity distributions (fields) of the tracers (TiO₂ particles or droplets) in the flow were recorded between the laser pulses. The average velocity of the tracing particles was calculated by averaging all the data obtained during the recording. The systematic error of the instantaneous U_d and U_g calculation depended on the size of the recording area as well as the inter-frame latency. The systematic error was 0.065 m/s, while the random errors (based on averaged measurements) were under 0.08 m/s.

Apart from the size of individual droplets, we needed to know the size distribution of droplets in an aerosol flow (to provide stable initial conditions in the series of experiments). For that, we used such techniques as interferometric particle imaging (IPI) and shadow photography (SP). These experiments were conducted simultaneously with the PIV measurements of the droplet flow velocity. The IPI technique was used for water aerosol flow without impurities and the SP technique for the graphite slurry aerosol. The interferometric method is an order of magnitude more accurate than SP when identifying the dimensions of small (R_d < 0.3 mm) droplets. However, IPI can only provide a clear interference pattern only for optically transparent media; hence, using it for the graphite slurry was out of the question. Below is a short description of the methods we used.

The IPI method derives the droplet size from the interference pattern on its defocused image. The interference is observed between the laser light refracted and reflected off the droplets due to the difference in refraction coefficients of the air and water media [12]. The equipment used in the experiments, as well as its settings and configuration, are the same as in the PIV technique described previously. The experiment was performed in two stages. At the first stage, the camera was focused on the droplets in the light sheet plane, just like in the PIV technique (approx. 300 mm distance between the camera lens and the recording area). At the second stage, the camera was shifted (defocused) from the light sheet plane (the defocus distance was approx. 25 mm). This way, we obtained the droplet images—circles with a set of interference fringes perpendicular to the light sheet direction. A slit aperture installed on the camera lens was used to prevent the images from overlapping and to simplify their subsequent analysis. This device transformed the round-shaped image into a thin line with vertical interference fringes. About 200 flow images were filmed. Using the Actual Flow software algorithm, we searched for the images and calculated R_d, since that the droplet size is known [16] to be proportional to the interference fringe frequency. Then we plotted the final size distribution of droplets in the flow. The systematic error of the R_d calculation was 0.002 mm [12].

Shadow Photography (SP) is a popular technique. The equipment used for it is similar to the one used for PIV and described above. The difference was in the lens, which was Nikon Micro-Nikkor 200 mm f/4D ED-IF A, as well as in the use of background illumination instead of the light sheet that cut the flow. In this case, light system 12 (Figure 1) was a diffusion screen connected to the laser by the optical fiber and installed in front of the camera. The laser light diffused by the screen provided a contrast shadow image of the droplets. About 300 images of the flow were recorded. Their further processing is typical of the shadow techniques [20,21]. A Median Filter was used to smooth the background noise. The Laplace Edge Detection Filter highlighted the borders of the droplets. The Low Pass Filter smoothed the droplet boundaries. Binarization was used to screen the droplets outside the focal depth of the camera (the droplets with blurred borders). The radii were calculated for the droplets remaining after the screening process. The systematic error of the SP technique for the R_d calculation corresponded to the scaling coefficient (s) and amounted to 0.007 mm.

In the video frame analysis, we calculated the probabilities (P₁—coalescence, P₂—separation, P₃—disruption, P₄—bounce) as the number of collisions with the corresponding outcomes under identical parameters to the total number of collisions. For example, P₁ = n₁/(n₁ + n₂ + n₃ + n₄), P₂ = n₂/(n₁ + n₂ + n₃ + n₄), etc. Thus, the values P₁, P₂, P₃, and P₄ added up to 1. The term probability was introduced to numerically estimate the frequency of collisions in the given modes. The statistical analysis of the experimental results was carried out by processing at least 50 droplet interactions under identical conditions. The algorithm was developed in the Mathematica software to select frames with approaching droplets. It enabled us to select 500–1000 frames (from the original 3000–5000) under identical experimental conditions to ensure the reliable statistics of collisions.

We calculated the Weber number of the approaching droplets before the collision, considering the relative velocity of the oncoming motion: We = 2ρR_dU_rel²/σ. U_rel, R_d, values were determined from the experimental video frames.

Table 1. Main properties of liquids.

Liquid	Temperature, T (°C)	Density ρ (kg/m3)	Surface Tension, σ∙103 (N/m)	Dynamic Viscosity, µ∙106 (Pa∙s)
Water	20/80	998/965	72/63	1004/282
Slurry	20	1030	73	1100
Milk [39,40]	20	1041	47	4300
Water [32]	20–22	995–1000	72–73	1000–1010

presents the values of the main properties (density, viscosity, and surface tension) of the liquids under study, which were required for the generalization and analysis of the experimental results, as well as their comparison with the data obtained by other authors.

When conducting experiments in the framework of this study, we did not carry out the special purification of liquids in order to meet the conditions characteristic of various applications described in the article (purification of liquids, atomization of fuels, gas-vapor-droplet heat exchangers, etc.). By adding surfactants or contaminants, droplet collision modes can be controlled. In particular, mode maps and characteristics of collisions of liquid droplets with surfactants or contaminants are given in [41]. Since, in real technologies, the presence of various impurities in the droplets is possible, and their concentration may change during the process (for example, due to evaporation or burnout), it is further advisable to study the processes of collisions of liquid droplets in an aerosol with the addition of surfactants or contaminants.

In this study, we tried to calculate the number of liquid fragments (droplets of different shapes and sizes) formed in the collisions and their total surface area. The tracking algorithms of Tema Automotive were used as in [42]. Figure 2 presents the scheme used to record the parameters and calculate all the main characteristics of the interaction process.

Before the collision, the total area of the free surface of primary droplets was given by S = 4πR_d². Before the interaction, the initial area of the liquid surface (S₀) equaled the sum of the corresponding droplet areas (projectile and target). After the collision, the newly-formed liquid fragments had different shapes and sizes. The sizes of all the possible configurations of liquid fragment surfaces appear quite difficult to analyze in detail. Therefore, it was assumed that all the water fragments resulting from the interaction of the primary droplets were spherical in shape. Thus, we calculated the total surface area of liquid droplets after collision (S₁).

In processing the experimental results, the assumption was made of the spherical shape of the droplets. In preliminary experiments, it was found that if such an assumption is not accepted, but real forms are taken into account, the process of processing experimental data takes significantly longer. At the same time, the differences, for example, in the frequencies of realization of one or another collision mode, do not exceed 5%–7%.

2.2. Factors under Investigation

In the Introduction Section, we mentioned potential applications of the results of the experimental research into droplet collision processes in the gas medium. With these in mind, we have made a list of the most significant factors, effects, and processes that can considerably change not only the quantitative values of droplet collision characteristics but also the interaction mode. These factors [15,16,17,19,20,21,25,42], with an emphasis on gas-vapor-droplet applications, are listed below, along with the ranges of varying the corresponding parameters to consider their influence:

• Droplet sizes. In typical aerosol technologies, typical droplet sizes can change severalfold within the main range, from 0.1 to 5 mm. So, it is reasonable to vary the R_d1 and R_d2 ratio values from 0.1 to 2.
• Relative velocity of droplets. Droplet collisions in aerosols in one plane are most common. Under such conditions, droplet motion vectors are normally co-directional or opposite. Calculating the relative velocity of motion becomes much simpler, as it is rational to take into account the difference or the sum of motion velocities of two droplets. In the dimensionless processing of experimental results, either the absolute motion velocity of one of the droplets or a typical mean value for the variable range of droplet velocity can be used as a scale coefficient. Considering different schemes of droplet interaction, it appears sensible to vary the dimensionless relative velocity of a droplet in the range between 0 and 10 for real-life aerosols.
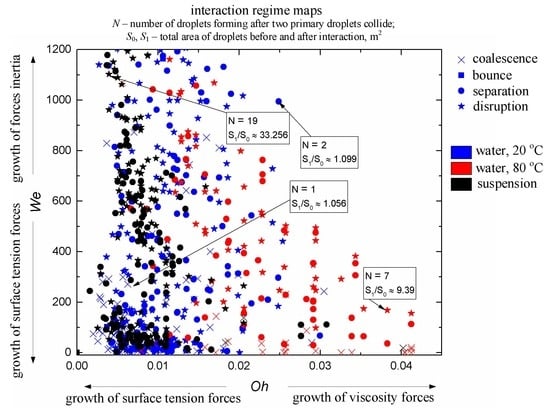
• The Weber number, characterizing the ratio of inertia to surface tension. This parameter is frequently used to describe the influence of droplet velocities and dimensions on their interaction parameters. According to the experimental studies of the last 50 years cited in the review papers [33,43,44], the We number can be found to range from 0 to 1000. This is the range, in which four main interaction modes are realized: bounce, separation, coalescence, and disruption.
• Impact (interaction) angle. The angular parameter of collision is calculated as a cosine of the interaction angle; the latter is defined as the angle between the relative velocity vector of droplets and their contact line [32] or between the trajectories, [34,43] notes that using this or that angular parameter of interaction is arguable. At a first approximation, both approaches can be used with varying the angle between droplet trajectories in the widest range, i.e., from 0° to 90°. Based on the data from [34,43], we can recalculate the experimental results to fit the techniques in [32].
• Droplet concentration in an aerosol. This parameter affects the frequency of droplet collisions. It is interesting to study its influence on the droplet interaction mode and typical outcomes. The variation range of γ_d can be quite wide to characterize all the possible atomization conditions. Since the volume of each droplet as an aerosol element is incomparably smaller than that of power plant chambers, the relative concentration range should be chosen in accordance with the mean droplet size in the aerosol.
• Temperature range in the droplet collision area, which depends on the temperature of both the gas medium (T_a) and liquid droplets (T_d). In accordance with the real-life gas-vapor-droplet applications, the most typical variation ranges for these parameters are up to 1000 °C for T_a and up to 100 °C for T_d. Using an air heater and compressor, as well as a flue gas generation system, similarly to the method in [20,21], we can vary these parameters in wide ranges.
• Turbulent, transition, or laminar flow regimes of the carrier medium. Typical spraying and irrigation systems feature different motion regimes of the aerosol in general and single droplets as its elements. Thus, the Reynolds number for the carrier gas medium can vary from several dozen to several thousand. It is important to vary the characteristic values for such a wide Re range. For instance, it is reasonable to consider the range up to 3000 for typical systems using flows based on flue gases.
• Dimensionless parameters of droplet interaction. Traditionally, two types of interaction parameters are used: linear (B) and angular (β). The angular parameter was calculated by the formula β = cos(α_d), whereas the linear one took into account the impact parameter B = b/(R_d1 + R_d2). The typical range of varying these parameters is 0 to 1 [43].
• Heterogeneity in droplet composition. In this case, we draw up interaction parameter maps using the Ohnesorge, Laplace, Reynolds, and capillary numbers. The characteristic variation ranges of Oh, La, Ca, and Re in such maps can differ, but they are generally comparable to the known data for water. Thus, we can evaluate the effect of viscosity, surface tension, density, and other properties of liquids on droplet transformation characteristics. The analysis of [33,43,44] shows that there is a lot of data for droplets of homogeneous liquids, solutions, and emulsions. So, it is slurry compositions that attract attention as the object of research. The influence of concentration and size of solid particles on lamination and other processes is traditionally extensively discussed (an overview of this issue is presented in [42]). In this study, we selected the mean values of these parameters in accordance with the concepts in [42] (to provide for a further assessment for different technologies, in which these parameters vary in wide ranges, sometimes severalfold): the graphite particles used were 40–50 µm in size, and their relative mass fraction was 5%.
• Ratios of initial surface areas of interacting droplets and their roles: target or projectile. The results of processing the experimental data on liquid droplet interaction are often generalized with no emphasis on the droplet role. The experiments [20,21] have shown that pre-collision projectiles and targets can differ not only in size and velocity but also in shape. This factor should be taken into account when data is generalized, and especially when the outcomes of droplet collision are analyzed. It makes sense to determine the average number of new droplets N and the ratio S₁/S₀.

Further, you will find the results of research into these factors, their discussion, and the main graphic illustrations obtained with the use of the statistical and phenomenological approaches. All the key diagrams and curves present N and S₁/S₀ values to allow for a comparative analysis of the contribution each factor makes to the main characteristics of secondary droplet atomization (liquid atomization is a primary task in the above applications). A comparative analysis can optimize secondary atomization if simpler and less costly approaches are chosen.

The parameters of the gaseous medium have a significant effect on the regimes of collisions of liquid droplets [45,46], since the ratios of inertial forces, viscosity, and surface tension change. In the present work, the air was used as a gaseous medium. The properties of air (for example, viscosity and density) within the varied ranges did not change significantly. Therefore, in this work, this factor could be neglected. In other environments, for example, in a gas-vapor mixture based on combustion products, droplets and vapor of liquids, the density, viscosity, and component composition of the gas mixture can have a significant effect on the modes of collisions.

3. Results and Discussion

Table 2. Registered and calculated parameters of droplet interaction.

No. of collision under study	1	…	1012
ɑd—impact angle, °	5	…	0
Rd1—radius of the first droplet, mm	0.253	…	0.151
Rd2—radius of the first droplet, mm	0.301	…	0.334
Ud1—velocity of the first droplet, m/s	1.823	…	2.93
Ud2—velocity of the second droplet, m/s	2.431	…	3.13
b—distance between droplet centers of mass, mm	0.234	…	0.409
Interaction mode	Bounce	…	Disruption
No. of frame	22	…	3297
Shape of the first droplet	sphere	…	sphere
Shape of the second droplet	sphere	…	sphere
N—number of post-collision droplets	2	…	14
Type of droplet interaction	co-directional	…	head-on
Rd1/Rd2	0.841	…	0.452
Urel—resulting velocity of droplets after interaction, m/s	0.6	…	6.06
B [b/(Rd1 + Rd2)]	0.423	…	0.844005
β [cos(ɑd)]	0.996	…	1
…	…	…	…

presents an example of typical primary results of the experiments and generalizing criteria derived from them. In our study, we used this technique to process the records of more than 1000 liquid droplet collisions. We can generally assume that an extensive database has been formed to analyze the influence of the above ten groups of factors and the corresponding processes characteristic of gas-vapor-droplet applications. Three important factors can have the most powerful and predictable influence on the modes and outcomes of liquid droplet collision: size, velocity, and impact angle. The first two are traditionally the constituents of the general criterion expression—the Weber number.

Figure 3 and Figure 4 present the curves illustrating the influence of these factors on the frequency of each of these four interaction modes. The overview of experimental findings made it obvious that the role of droplet size and velocity should be analyzed using the respective ratios shown in Figure 3 and Figure 4, rather than the absolute values. Apart from the three above factors, changes in the droplet surface shape due to continuous transformation and droplet roles (target or projectile) can have considerable influence as well.

Figure 3 and Figure 4 present the differences in the frequency of collision modes (P₁, P₂, P₃, and P₄) when the ratios of radii and velocities are less than 1 (the values of the corresponding parameters for the projectile are lower than those for the target) and more than 1 (the opposite situation). The numerical values of process characteristics (research findings) for the dominant outcomes of droplet interaction in aerosols are of the greatest value in the conducted experiments. If necessary, the established values of P₁, P₂, P₃, P₄ (Figure 3 and Figure 4) can be used to outline the region of parameters ensuring stable coalescence, bounce, separation, and disruption of droplets of different shapes and roles (target and projectile). The main feature of such regions is in the dominance of different outcomes of the collision of droplets having the shape of a sphere, ellipsoid, and flat disk. Thus, in the interaction of spheres, coalescence, and bounce (high P₁ and P₄ values) dominate. Colliding ellipsoids feature high values of separation (P₂), whereas flat disks have high P₂ and P₃. These patterns mainly stem from different values of forces (inertia, friction, etc.) acting on droplets of different shapes during their motion in the gas medium. In particular, disk-shaped droplets are subjected to several times greater resistance force than sphere-shaped droplets are. This results in the instability of the non-spherical droplet surface even with lower (as compared to spheres) values of velocity and size (lower Weber number, accordingly).

Ellipsoid-shaped droplets have rather high values of P₂ throughout the whole range of collision angles. This nontrivial result indicates that the position of ellipsoids relative to each other or to a spherical droplet does not actually have an effect on the interaction outcomes. When the projectile hit the central part of the ellipsoid-shaped target at any angle, separation was observed. Intensive disruption, corresponding to droplet breakup, only occurred when the projectile hit the side (tail) parts.

Consistent patterns have been established for disk-shaped targets, which are similar to the ones outlined for ellipsoids. However, an increase in the collision angle resulted in a severalfold higher frequency of separation. This results from the fact that a flat disk is basically a conglomerate of a large number of water chains, which get thinner at higher velocity (this increases the transversal dimensions and reduces the longitudinal ones, i.e., thickness). When the projectile hits such chains, it breaks through them and usually retains its initial size, thus causing a typical separation of colliding fragments of liquid (so, the values of P₂ are high). At smaller initial dimensions and velocities of droplets, frequent coalescence (higher P₁ values) was recorded for the collisions of spheres and flat disks. At a narrow angle of collisions of spheres and flat disks, the interaction between the projectile droplet and water chains in flat disks occurred at a tangent. Thus, the contact area increased. This led to a lower frequency of separation and a more intensive breakup (usually considerable fragmentation) of both of the droplets.

It was established that in the whole variation range of the impact angle (0°–90°), interactions are recorded that result in a complete or partial fragmentation (breakup) of droplets. Such conditions were recorded for large dimensions (0.5–1 mm) and velocities (7–10 m/s) of at least one of the droplets. Nonspherical droplets have lower values of radii R_d1, R_d2 and velocities U_d1, U_d2. This result might seem quite obvious, but we were the first to establish the differences in the collision angle ranges for droplets having the shape of spheres, flat disks, and ellipsoids, where bounce, coalescence, separation, and disruption dominate. High values of velocity (over 7 m/s) and size (over 0.5 mm) of droplets (the Weber number over 50) are characterized not only by the interaction with the breakup, as it could be expected. High frequency values were recorded for separation and coalescence. This result can be explained by the influence of collision angles and droplet shapes, which are not taken into account when calculating the Weber number.

A good agreement between our experiments and those in [25,26] is only established when We > 50. At lower values of We, the probability of transition between coalescence and separation and then disruption differs by 20%–30%. This result is likely to reflect the roles of collision angles and shapes of the interacting droplets. Unlike the experiments in [25,26], we recorded different interaction schemes in all the Weber number variation ranges (at impact angles from 0° to 90°). Thus, even at We < 15, conditions were established with a high frequency of coalescence, as well as separation and disruption (of projectiles and targets).

Figure 5, Figure 6 and Figure 7 present the results of studying the contribution of yet understudied effects and factors, such as the relative concentration of droplets in the aerosol, the temperature in the droplet collision region, and the degree of turbulence of the droplet flow. Overall, the generalization of Figure 5, Figure 6 and Figure 7 shows that each of these factors influences the aerosol structure and intensifies droplet collisions.

It can be clearly seen in Figure 5 that the number of droplet collisions rises significantly when their relative concentration in aerosol is increased. Predictably, however, the droplet disruption does not dominate (the trends are more complicated due to a strong connection with the relative velocity of droplets, as well as ratios of their sizes). The growth of droplet concentration intensifies all the interaction modes, especially coalescence and disruption, as shown in Figure 5. Only when the We values are high, the frequencies of disruption and separation predominate significantly over bounce and coalescence. Figure 5 can be used to predict the conditions when the flow changes greatly in the disruption and coalescence modes, and weakly during separation and bounce.

The gas-droplet medium temperature in the region of liquid fragment collision can change both due to different initial temperatures of droplets and various temperatures of the gas medium. Heating the gas-vapor-droplet medium leads to an increase in the number of collisions in the regimes of coalescence, and especially bounce, and to a reduction in the number of interactions with separation and disruption of droplets. Such trends are particularly obvious in the range of average and low values of We in Figure 6. This effect is explained by the vapor concentration growth promoted by the intensification of droplet heating in the gas medium. This results in a higher pressure of the gas-vapor mixture acting on each of the droplets. Since the vector of vapor jetting from the droplet surface is always in the opposite direction to the droplet movement, this effect slows down the latter process. Consequently, the kinetic energy of moving liquid fragments decreases. Droplets bounce off each other without breakup or coalescence. Bounces become more frequent. The formation of a buffer vapor layer around liquid fragments can fail to have a significant effect only at high initial velocities of droplets, because the linear velocities of vapor outflow cannot exceed several decimeters per s, even during rapid vapor formation.

The gas-vapor-droplet flow agitation leads to a substantial violation of trends of changing P₁, P₂, P₃, and P₄ as functions of We (Figure 7). In particular, at low values of the Reynolds number of gases (under 1100), we recorded predictable trends of growing relative frequency of disruption and separation, and of decreasing coalescence and bounce at higher We. At average (2400) and high (2800) values of the Reynolds number of gases in Figure 7, we can see that the disruption and separation frequency variations are no longer steady, whereas the trends are retained for coalescence and bounce. This is likely to be caused by the fact that the agitation of the gas-vapor-droplet flow leads to a significant change not as much in the linear velocities of droplets as in the velocities of rotational motion and deformation. Consequently, rotating droplets interact more often in the separation regime, especially when their velocity goes up (Figure 7). Thus, even under severe turbulence, a stable structure of the gas-vapor-droplet flow can be maintained (as separation does not lead to a growth in the droplet number or changes in their initial sizes).

Figure 8 and Figure 9 present droplet interaction regime maps obtained using the angular (β) and linear (B) parameters of droplet collision. They are intended to illustrate the variation ranges of the key characteristics of collisions, in which each of the four regimes is always realized: bounce, coalescence, separation, and disruption. The Weber number takes into account the droplet velocity and size, whereas β and B are based on the impact angle and impact parameter.

The maps in Figure 8 and Figure 9 demonstrate that if we take into account the range of the Weber number variation alone, it is impossible to provide a reliable prediction of coalescence, separation, disruption, or even bounce (in [25,26], conclusions were drawn that the latter occurs only at 0.5 < We < 1.5). In our experiments, depending on β and B values, bounce occurred at much higher We values as well, especially under the conditions of intensive droplet evaporation. Unlike the known data of other authors presented in Figure 8 and Figure 9, the regime maps in this research were obtained by recording more than 1000 collisions of aerosol cloud elements. The motion of droplet groups in different directions and with a relatively high droplet concentration results in their significant influence on collisions between one another and even many of the droplets moving around them. This explains why the transient areas in Figure 8 and Figure 9 (obtained when recording the collisions of two single droplets) do not look the same as other authors’ data. However, the common trend remains for these transient areas to shift when varying We from 0 to 200 and β and B from 0 to 1 in this study and in [32,39]. In particular, the droplet coalescence mode is clearly seen to dominate throughout the whole β and B range, and at We < 40; disruption dominates at We > 150 and for any given β and B. In the range 30 < We < 120, three modes can be realized: disruption, separation, and coalescence. The parameters β and B have a decisive influence.

The analysis of recent studies on the characteristics of heterogeneous droplet collision (emulsions, solutions, slurries, and immiscible fluids) [33,44] shows that not only inertia and surface tension but also internal friction (viscosity) have a dominant influence. Figure 10 and Figure 11 present interaction regime maps with criterial processing using the Weber number (We) (which considers both velocity and size, but changes differently when they are varied; the outcomes change differently), the Reynolds number (Re) (which considers velocity, size, and viscosity), the Ohnesorge number (Oh) (which considers density, size, viscosity, and surface tension), the Laplace number (La) also known as the Suratman number (which considers density, size, viscosity, and surface tension), and the capillary number (Ca) (which considers viscosity, velocity, and surface tension). According to [33,44], the most typical coordinate systems to define regime maps of droplet interaction are Re(Oh), We(Oh), and We(Ca). La is often used instead of Oh, considering that La = 1/Oh² = Re²/We. Using such similarity criteria, we can analyze the joint influence of the main liquid properties (density, surface tension, and viscosity) and forces on droplet collision modes. Our objective in this study was to draw up the regime maps of Re(Oh), We(Oh), and We(Ca) using the statistical approach rather than the phenomenological one used in the experiments in [33,44]. This is the reason why the transient areas between droplet coalescence, separation, and disruption established in this study are different from the data in [33,44].

In the Re(Oh) and We(Oh) charts, we can evaluate the contribution of inertia, viscosity, and surface tension when defining any given droplet interaction mode. In the We(Ca) chart, we can evaluate the contribution of inertia, friction, and surface tension. The analysis of Figure 10 and Figure 11 shows that the liquids under study have a considerable difference in the ratio of these forces when varying the key experimental parameters discussed above and when comparing the experimental results for water at room temperature and high temperatures, as well as for slurries (the difference is especially noticeable in viscosity, density, and surface tension).

Under normal conditions, the differences in the surface tension coefficients for water and slurries with the relative mass fraction of solid particles of less than 5% do not exceed 4%–7%. At high concentrations of the disperse phase, the surface tension increases substantially, and droplet disruption requires more energy. However, the experiments have shown that the higher the concentration of solid inclusions in a slurry droplet, the greater the surface transformation of the latter. This illustrates the impact of other forces (not only those related to surface tension), in particular, inertia and internal friction due to the nonuniform distribution of disperse phase particles in the droplet. During heating, the surface tension of water and water-based slurries decreases significantly (2–3 times). This is supposed to contribute to a rapid transformation of the droplet surface; however, the experiments show a somewhat different result. It is conditioned by the fact that liquid or slurry droplets, when injected into the flue gas flow, are under higher pressure than the air flow (they compress), and their shape changes negligibly from the spherical one. The higher the temperature and velocity of the gas flow, the greater the slowdown of aerosol droplets in the flow. Hence, this is another case when not all the aspects of the droplet surface transformation are determined by the liquid surface tension.

The analysis of the regime maps obtained for homogeneous droplet interaction (water under normal conditions and when heated rapidly) in the Re(Oh) and We(Oh) coordinate systems shows that the lower the viscosity, the more rapidly the coalescence occurs. This holds true even at high We numbers, corresponding to separation and breakup in the β(We) and B(We) coordinate system, i.e., when inertia dominates over surface tension. This effect is highly prominent when viscosity forces dominate over surface tension, as well as when the temperature in the collision region increases, as the growth of the latter reduces viscosity and surface tension (e.g., in the case of water, 2–3 times when the temperature changes from 20 °C to 80–90 °C). If the ratio of viscosity forces to surface tension rises (illustrated by a higher Oh), a noticeable transition occurs from coalescence to disruption and separation. The reason for that is that under such conditions, the molecular bonds, ensuring the integrity of the near-surface layer weaken, and droplet breakup becomes quite difficult to avoid. However, due to high viscosity, the newly-formed liquid fragments quickly take a stable shape.

The experiments showed that the higher the surface tension of the liquid, the less often a rapid breakup occurs (separation being more frequent), but at high viscosity, droplet collisions produce more fragments than at low viscosity. This is because viscous fragments take stable spherical shapes quite fast, whereas low-viscosity droplets deviate from the spherical shape significantly when moving. This results in the slowdown of their motion and disruption. Thus, fewer liquid fragments are formed in collisions.

Analyzing the established experimental values in the We(Ca) coordinate system, we can see regions of stable coalescence (when surface tension forces dominate over friction and inertia). On the contrary, when We and Ca increase, there is a stable transition from coalescence to separation and disruption, as we would expect in accordance with the balance of the acting forces and their influence on the droplet surface transformation.

When generalizing the experimental data for droplet collisions, we established some important consistent patterns: the transition to the breakup (which contributes to a severalfold growth of S₁/S₀) is possible even at high surface tension and viscosity of the liquid. In line with the known concepts [27,28] of surface transformations of different liquid droplets in the field of the main forces, a rapid breakup is unavoidable at low viscosity and surface tension of the liquids. Under such conditions, the molecular forces, resulting from tension and internal friction, are weak. The experiments without collisions showed that the velocity of droplets under 5 m/s and their radii ranging from 1 to 3 mm are sufficient for their significant transformation and breakup with the formation of numerous fragments. In the case of droplet collisions, we found out that the interacting slurry droplets are characterized by minimal critical Weber numbers, which are enough for droplets to break up, despite the maximum values of surface tension and viscosity. When water is heated to 60–80 °C, viscosity and surface tension are, on the contrary, several times lower, whereas the critical Weber numbers are higher than for suspensions. This is explained by different modes of droplet collisions and the formation of differently-shaped structures in the interaction. To consider these specific features, we can use the obtained interaction regime maps (Figure 10 and Figure 11) in dimensionless We(Oh), Re(Oh), and We(Ca) coordinate systems.

The comparative analysis of slurry and water droplet collisions showed an important pattern: under identical interaction parameters, slurry droplets separated and broke up, while water droplets coalesced or separated. This result cannot be explained only by the difference between the surface tension of slurry and water since with the mass concentration of solid particles in the droplet under 10%, this parameter is almost identical to that of water (with 3%–5% differences). The local concentration of solid particles in one of the droplet parts (due to different densities) plays a great role; thus, the kinetic energy of the slurry droplet increases as compared to the water droplet. The video frames captured a direct contact of solid particles in the thin near-surface layer. Due to their collisions and bounces, the near-surface layers of both droplets were destroyed, which promoted droplet breakup (the higher the solid phase concentration, the larger-scale these effects). At moderate velocities (under 2 m/s) and relatively small droplet dimensions (under 1 mm), the colliding fragments separated, whereas, at higher ones (We > 40), they broke up.

The values N and S₁/S₀, established in the experiments, illustrate great prospects for using droplet collision effects for the growth of the interphase surface area and intensification of heat and mass transfer processes (Figure 12). Each of the factors (overheating, acceleration, and collision of droplets with one another or with a barrier), reviewed in the experiments in [42] and in this research, contribute effectively to an increase in the S₁/S₀ ratio. This result is remarkable for the development of heat and mass transfer technologies requiring intensification of phase transformations due to the secondary atomization of droplets. The latter can be achieved by a combined influence of the three factors above. It is important to take into account the consumption of energy for droplet acceleration, collision, or mixing of heterogeneous compositions. At the first approximation, the cheapest technologies appear to be the ones of secondary atomization of droplets, based on their collisions, as there is no need for more heat supply or significant flow acceleration. By varying the impact angles, shapes, dimensions, and concentrations of droplets, it is possible to ensure high values of S₁ to achieve the S₁/S₀ ratio of no less than 10. In this case (severalfold decrease in droplet size or total area of the liquid surface), the secondary atomization of droplets can be considered efficient and feasible.

It is clearly seen in Figure 12 that the normal distribution of new liquid fragments, obtained from the primary droplet collisions, remains the same for different compositions and ratios of inertia and surface tension. This result is essential for predicting the droplet dimensions of the aerosol obtained in the secondary atomization. Some shifts in the extrema relative to the central region of the size range in Figure 12 are explained by the generalization of all the experimental results, i.e., we averaged the values of all the experimental series while varying a large group of the above factors. If we select frames where only one of the 10 factors described in Section 2.2 is varied, the normal size distribution of newly-formed liquid fragments is maintained, with the average-sized droplets prevailing.

Thus, the conducted experiments made it possible to establish the variation ranges of two interaction parameters (β, B) and the Weber, Reynolds, Ohnesorge, Laplace, and capillary numbers, in which the conditions of stable bounce, coalescence, separation, and disruption were recorded for the most typical liquid compositions. Also, we defined the ranges of parameters, in which the realization of one of four interaction schemes has a non-deterministic nature (in the most commonly used coordinate systems based on β, B, We, Re, Oh, La, Ca parameters). Such experimental data push forward the development of droplet interaction models (in particular, the ones analyzed in [33,39,44,47].

4. Conclusions

(i) The scientific novelty and practical significance of the results are that a statistical database with droplet collision characteristics in aerosols has been created for the first time. It takes into account a wide group of factors: droplet size ratio, relative velocity, impact angles, concentration, surface area and shapes, angular and linear parameters of interaction, as well as typical similarity numbers (Weber, Reynolds, Ohnesorge, Laplace, capillary). In the case of droplet collisions in aerosols, there is major variability of experimental data. This is explained by a significant influence of neighboring droplets. Under such conditions, it is rational to use the statistical approach to process the experimental results, calculating the relative frequency of a given droplet collision mode. We used this scheme to show the contribution of each of the effects and factors under study and determine the conditions under which each of the four droplet collision modes (bounce, separation, coalescence, and disruption) dominates. This data is useful to develop primary and secondary atomization systems for different liquids.

(ii) Charts were obtained illustrating the influence of the factors, effects, and parameters under study. Relative dimensions and velocities of droplets featured the most significant effect, as well as dimensionless parameters of interaction (angular and linear). Thus, using the conventional regime maps of droplet interaction, for example, β(We), B(We), We(Oh), We(Ca), Re(Oh), it is rather difficult to describe the parameter variation ranges at which only one interaction regime occurs. In all the experiments, there were at least two or three collision regimes recorded under identical conditions of all the key parameters.

(iii) When comparing the data of other authors, obtained under ideal conditions, i.e., by recording the collisions of only two moving droplets (the phenomenological approach), conditions were defined when stable bouncing, coalescence, disruption, and separation occurred, as well as the parameter variation ranges, in which factors have a countervailing influence. Therefore, under identical interaction parameters, modern recording and processing techniques produce quite different results. The comparison of the experimental data shows the feasibility of using the phenomenological and statistical approaches for a more comprehensive understanding of the physics of droplet interaction in real-life gas-vapor-droplet technologies. In this case, it is possible to reliably predict the values of N and S₁/S₀ for any interaction regime and with any parameters (R_d, U_d, α_d, γ_d, β, T_a, T_d, We, Re, Oh, La, Ca, etc.) determining the ratios of inertia, surface tension, and viscosity.