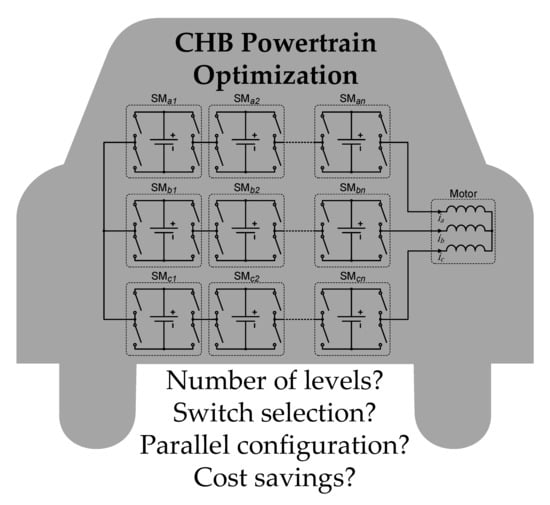
Optimization of a Cascaded H-Bridge Inverter for Electric Vehicle Applications Including Cost Consideration
Abstract
:1. Introduction
2. Method
2.1. Load Model
2.2. Inverter Loss Model
2.3. Cost Model
3. Results
3.1. Maximum Theoretical Savings Consideration
3.2. Optimal Results with “HC Model” Cost Consideration
3.3. Optimal Results with “LC Model” Cost Consideration
3.4. Optimal Results with “DSC Model”
3.5. Optimal Results with “VIC Model”
3.6. Optimal Results with “TOS Model” Cost Consideration
3.7. Summary of Optimal Results
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature and Abbreviation Glossary
| Variable | Definition | Abbrev. | Definition |
| Drain-source voltage | CHB | Cascaded H-Bridge | |
| Drain current | BEV | Battery Electric Vehicles | |
| Temperature coefficient | EV | Electric Vehicles | |
| Drain-source on resistance | MMC | Modular Multilevel Converters | |
| Resistance of the diode | SM | Sub-Modules | |
| Diode on-state voltage | OEM | Original Equipment Manufacturer | |
| Recovered charge of the diode | LC Model | Low cost model | |
| Gate-drain capacitance | HC Model | High cost model | |
| Gate-drain capacitance | DSC Model | Die size cost model | |
| Plateau voltage | VIC Model | Voltage-Current cost model | |
| Current time | TOS Model | Theoretical Optimal Switch Model |
References
- Kochhan, R.; Fuchs, S.; Reuter, B.; Burda, P.; Matz, S.; Lienkamp, M. An Overview of Costs for Vehicle Components, Fuels and Greenhouse Gas Emissions. Available online: http://www.researchgate.net/publication/260339436_An_Overview_of_Costs_for_Vehicle_Components_Fuels_and_Greenhouse_Gas_Emissions (accessed on 17 June 2019).
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. From Li-ion single cell model to battery pack simulation. In Proceedings of the 2008 IEEE International Conference on Control Applications, San Antonio, TX, USA, 3–5 September 2008; pp. 708–713. [Google Scholar]
- Rumpf, K.; Naumann, M.; Jossen, A. Experimental investigation of parametric cell-to-cell variation and correlation based on 1100 commercial lithium-ion cells. J. Energy Storage 2017, 14, 224–243. [Google Scholar] [CrossRef]
- Schuster, S.F.; Brand, M.J.; Berg, P.; Gleissenberger, M.; Jossen, A. Lithium-ion cell-to-cell variation during battery electric vehicle operation. J. Power Sources 2015, 297, 242–251. [Google Scholar] [CrossRef]
- Zhou, L.; Zheng, Y.; Ouyang, M.; Lu, L. A study on parameter variation effects on battery packs for electric vehicles. J. Power Sources 2017, 364, 242–252. [Google Scholar] [CrossRef]
- Baumann, M.; Wildfeuer, L.; Rohr, S.; Lienkamp, M. Parameter variations within Li-Ion battery packs—Theoretical investigations and experimental quantification. J. Energy Storage 2018, 18, 295–307. [Google Scholar] [CrossRef]
- Baumhöfer, T.; Brühl, M.; Rothgang, S.; Sauer, D.U. Production caused variation in capacity aging trend and correlation to initial cell performance. J. Power Sources 2014, 247, 332–338. [Google Scholar] [CrossRef]
- Chang, F.; Roemer, F.; Baumann, M.; Lienkamp, M. Modelling and Evaluation of Battery Packs with Different Numbers of Paralleled Cells. World Electr. Veh. J. 2018, 9, 8. [Google Scholar] [CrossRef]
- Cao, J.; Schofield, N.; Emadi, A. Battery balancing methods: A comprehensive review. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1–6. [Google Scholar]
- Thomitzek, M.; Schmidt, O.; Röder, F.; Krewer, U.; Herrmann, C.; Thiede, S. Simulating Process-Product Interdependencies in Battery Production Systems. Procedia CIRP 2018, 72, 346–351. [Google Scholar] [CrossRef]
- Helling, F.; Gotz, S.; Weyh, T. A battery modular multilevel management system (BM3) for electric vehicles and stationary energy storage systems. In Proceedings of the 2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 26–28 August 2014; pp. 1–10. [Google Scholar]
- Li, Y.; Han, Y. A Module-Integrated Distributed Battery Energy Storage and Management System. IEEE Trans. Power Electron. 2016, 31, 8260–8270. [Google Scholar] [CrossRef]
- Peng, F.Z.; Qian, W.; Cao, D. Recent advances in multilevel converter/inverter topologies and applications. In Proceedings of the 2010 International Power Electronics Conference—ECCE ASIA-, Sapporo, Japan, 21–24 June 2010; pp. 492–501. [Google Scholar]
- Tolbert, L.M.; Peng, F.Z.; Habetler, T.G. Multilevel converters for large electric drives. IEEE Trans. Ind. Appl. 1999, 35, 36–44. [Google Scholar] [CrossRef]
- Tolbert, L.M.; Peng, F.Z.; Habetler, T.G. Multilevel inverters for electric vehicle applications. In Proceedings of the Power Electronics in Transportation (Cat. No.98TH8349), Dearborn, MI, USA, 22–23 October 1998; pp. 79–84. [Google Scholar]
- Li, N.; Gao, F.; Yang, T.; Zhang, L.; Zhang, Q.; Ding, G. An integrated electric vehicle power conversion system using modular multilevel converter. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 5044–5051. [Google Scholar]
- Quraan, M.; Yeo, T.; Tricoli, P. Design and Control of Modular Multilevel Converters for Battery Electric Vehicles. IEEE Trans. Power Electron. 2016, 31, 507–517. [Google Scholar] [CrossRef]
- Chang, F.; Ilina, O.; Lienkamp, M.; Voss, L. Improving the Overall Efficiency of Automotive Inverters Using a Multilevel Converter Composed of Low Voltage Si MOSFETs. IEEE Trans. Power Electron. 2019, 34, 3586–3602. [Google Scholar] [CrossRef]
- Chang, F.; Ilina, O.; Hegazi, O.; Voss, L.; Lienkamp, M. Adopting MOSFET multilevel inverters to improve the partial load efficiency of electric vehicles. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.13. [Google Scholar]
- Sarrazin, B.; Rouger, N.; Ferrieux, J.; Crebier, J. Cascaded Inverters for electric vehicles: Towards a better management of traction chain from the battery to the motor? In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 153–158. [Google Scholar]
- Patel, D.; Saravanakumar, R.; Ray, K.K.; Ramesh, R. Design and implementation of three level CHB inverter with phase shifted SPWM using TMS320F24PQ. In Proceedings of the India International Conference on Power Electronics 2010 (IICPE2010), New Delhi, India, 28–30 January 2011; pp. 1–6. [Google Scholar]
- Xiao, M.; Xu, Q.; Ouyang, H. An Improved Modulation Strategy Combining Phase Shifted PWM and Phase Disposition PWM for Cascaded H-Bridge Inverters. Energies 2017, 10, 1327. [Google Scholar] [CrossRef]
- Lee, J.-S.; Sim, H.-W.; Kim, J.; Lee, K.-B. Combination Analysis and Switching Method of a Cascaded H-Bridge Multilevel Inverter Based on Transformers With the Different Turns Ratio for Increasing the Voltage Level. IEEE Trans. Ind. Electron. 2018, 65, 4454–4465. [Google Scholar] [CrossRef]
- Miranbeigi, M.; Neyshabouri, Y.; Iman-Eini, H. State feedback control strategy and voltage balancing scheme for a transformer-less STATic synchronous COMpensator based on cascaded H-bridge converter. IET Power Electron. 2015, 8, 906–917. [Google Scholar]
- Majed, A.; Salam, Z.; Amjad, A.M. Harmonics elimination PWM based direct control for 23-level multilevel distribution STATCOM using differential evolution algorithm. Electr. Power Syst. Res. 2017, 152, 48–60. [Google Scholar] [CrossRef]
- Pereda, J.; Dixon, J. 23-Level Inverter for Electric Vehicles Using a Single Battery Pack and Series Active Filters. IEEE Trans. Veh. Technol. 2012, 61, 1043–1051. [Google Scholar] [CrossRef]
- Maharjan, L.; Yamagishi, T.; Akagi, H.; Asakura, J. Fault-Tolerant Operation of a Battery-Energy-Storage System Based on a Multilevel Cascade PWM Converter with Star Configuration. IEEE Trans. Power Electron. 2010, 25, 2386–2396. [Google Scholar] [CrossRef]
- Monopoli, V.G.; Ko, Y.; Buticchi, G.; Liserre, M. Performance Comparison of Variable-Angle Phase-Shifting Carrier PWM Techniques. IEEE Trans. Ind. Electron. 2018, 65, 5272–5281. [Google Scholar] [CrossRef]
- Vahedi, H.; Sharifzadeh, M.; Al-Haddad, K.; Wilamowski, B.M. Single-DC-source 7-level CHB inverter with multicarrier level-shifted PWM. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 4328–4333. [Google Scholar]
- Xiao, B.; Hang, L.; Riley, C.; Tolbert, L.M.; Ozpineci, B. Three-phase modular cascaded H-bridge multilevel inverter with individual MPPT for grid-connected photovoltaic systems. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 468–474. [Google Scholar]
- Yu, Y.; Konstantinou, G.; Hredzak, B.; Agelidis, V.G. Operation of Cascaded H-Bridge Multilevel Converters for Large-Scale Photovoltaic Power Plants Under Bridge Failures. IEEE Trans. Ind. Electron. 2015, 62, 7228–7236. [Google Scholar] [CrossRef]
- Ebadpour, M.; Bagher, M.; Sharifian, B. Cascade H-Bridge Multilevel Inverter with Low Output Harmonics for Electric/Hybrid Electric Vehicle Applications. Int. Rev. Electr. Eng. (IREE) 2012, 7, 3248–3256. [Google Scholar]
- Sarrazin, B.; Rouger, N.; Ferrieux, J.P.; Avenas, Y. Benefits of cascaded inverters for electrical vehicles’ drive-trains. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 1441–1448. [Google Scholar]
- Pavlovic, J.; Ciuffo, B.; Fontaras, G.; Valverde, V.; Marotta, A. How much difference in type-approval CO2 emissions from passenger cars in Europe can be expected from changing to the new test procedure (NEDC vs. WLTP)? Transp. Res. Part A Policy Pract. 2018, 111, 136–147. [Google Scholar] [CrossRef]
- Advanced Powertrain Research Facility (APRF) at Argonne National Laboratory. Test Summary Sheet of BMW i3 BEV. Available online: https://www.anl.gov/es/energy-systems-d3-2014-bmw-i3bev (accessed on 17 June 2019).
- United States Environmental Protection Agency. EPA Fuel Economy Estimates. Available online: https://www.fueleconomy.gov/feg/PowerSearch.do?action=noform&path=1&year1=1984&year2=2019&vtype=Electric (accessed on 3 May 2019).
- Graovac, D.; Pürschel, M.; Andreas, K. MOSFET Power Losses Calculation Using the Data-Sheet Parameters. Infineon Appl. Note 2006, 1, 1–23. [Google Scholar]
- IPC—Association Connecting Electronics Industries. IPC-9592 Performance Parameters for Power Conversion Devices; IPC: Bannockburn, IL, USA, 2007; p. 93. [Google Scholar]
- Burkart, R.; Kolar, J.W. Component Cost Models for Multi-Objective Optimizations of Switched-Mode Power Converters. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 2139–2146. [Google Scholar]
- Domingues-Olavarria, G.; Fyhr, P.; Reinap, A.; Andersson, M.; Alakula, M. From Chip to Converter: A Complete Cost Model for Power Electronics Converters. IEEE Trans. Power Electron. 2017, 32, 8681–8692. [Google Scholar] [CrossRef]
- Octopart Inc. Octopart—Search Engine for Electronic Parts. Available online: https://octopart.com/ (accessed on 6 May 2019).
- Xiao, Y.; Shah, H.N.; Natarajan, R.; Rymaszewski, E.J.; Chow, T.P.; Gutmann, R.J. Integrated Flip-Chip Flex-Circuit Packaging for Power Electronics Applications. IEEE Trans. Power Electron. 2004, 19, 515–522. [Google Scholar] [CrossRef]
- Liu, X.; Jing, X.; Lu, G.-Q. Chip-scale packaging of power devices and its application in integrated power electronics modules. IEEE Trans. Adv. Packag. 2001, 24, 206–215. [Google Scholar]
- United Nations Addendum 99: Regulation No. 100; United Nations: New York City, NY, USA, 2013; Volume 2, pp. 1–82.
- BMW Group PressClub. The New BMW i3 94Ah. Available online: https://www.press.bmwgroup.com/united-kingdom/article/detail/T0259612EN_GB/the-new-bmw-i3-94ah?language=en_GB (accessed on 7 May 2019).
- BMW AG. Service and Warranty Information 2016 BMW i3. Available online: https://www.bmwusa.com/content/dam/bmwusa/warranty-books/2016/2016 BMW i3 SW.pdf (accessed on 17 June 2019).
- BMW Group PressClub. The New 2017 BMW i3 (94 Ah): More Range Paired to High-Level Dynamic Performance. Available online: https://www.press.bmwgroup.com/usa/article/detail/T0259560EN_US/the-new-2017-bmw-i3-94-ah-more-range-paired-to-high-level-dynamic-performance (accessed on 17 June 2019).
- Lima, P. Samsung SDI 94 Ah Battery Cell Full Specifications. Available online: https://pushevs.com/2018/04/05/samsung-sdi-94-ah-battery-cell-full-specifications/ (accessed on 17 June 2019).
- Harlow, J.E.; Ma, X.; Li, J.; Logan, E.; Liu, Y.; Zhang, N.; Ma, L.; Glazier, S.L.; Cormier, M.M.E.; Genovese, M.; et al. A Wide Range of Testing Results on an Excellent Lithium-Ion Cell Chemistry to be used as Benchmarks for New Battery Technologies. J. Electrochem. Soc. 2019, 166, A3031–A3044. [Google Scholar] [CrossRef]










| Attribute | HC Model | LC Model | DSC Model | VIC Model |
|---|---|---|---|---|
| Min. cost in USD | 0.38 | 0.02 | 0.31 | 0.33 |
| Max. cost in USD | 6.88 | 3.65 | 1.21 | 1.76 |
| Avg. cost in USD | 2.61 | 0.87 | 0.84 | 0.87 |
| Attribute | No Cost | HC Model | LC Model | DSC Model | VIC Model | TOS Model | Avg. of Cost Models |
|---|---|---|---|---|---|---|---|
| Min. Number of Modules | 10 | 3 | 3 | 2 | 2 | 2 | 2.4 |
| Max. Number of Modules | 27 | 6 | 5 | 5 | 5 | 7 | 5.6 |
| Avg. Number of Modules | 17.45 | 4.08 | 4.12 | 3.62 | 3.62 | 4.18 | 3.9 |
| Best Number of Modules | 17 | 3 | 4 | 3 | 3 | 3 | 3.2 |
| Most Number of Modules | 13 | 3 | 5 | 3 | 3 | 3 | 3.4 |
| Freq. of Most Module | 12 | 43 | 44 | 52 | 46 | 23 | 41.6 |
| Min. Num. of Parallel Sw. | 19 | 2 | 2 | 2 | 2 | 4 | 2.4 |
| Max. Num. of Parallel Sw. | 30 | 30 | 30 | 24 | 20 | 26 | 26 |
| Avg. Num. of Parallel Sw. | 26.56 | 11.67 | 15.12 | 9.09 | 7.16 | 13.33 | 11.27 |
| Most Num. of Parallel Sw. | 30 | 7 | 7 | 6 | 6 | 10 | 7.2 |
| Max. Efficiency in % | 99.8 | 99.4 | 99.44 | 99.33 | 99.35 | 99.2 | 99.34 |
| Avg. Efficiency in % | 99.77 | 99.00 | 98.6 | 99.00 | 99.00 | 98.69 | 98.86 |
| Max. Cost Savings in USD | 3488 | 2776 | 3065 | 2911 | 2998 | 2634 | 2877 |
| Avg. Switch Costs in USD | 0 | 1371 | 946 | 1102 | 1107 | 1167 | 1139 |
| Avg. Cost Savings in USD | 3476 | 2422 | 2925 | 2705 | 2708 | 2473 | 2647 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roemer, F.; Ahmad, M.; Chang, F.; Lienkamp, M. Optimization of a Cascaded H-Bridge Inverter for Electric Vehicle Applications Including Cost Consideration. Energies 2019, 12, 4272. https://doi.org/10.3390/en12224272
Roemer F, Ahmad M, Chang F, Lienkamp M. Optimization of a Cascaded H-Bridge Inverter for Electric Vehicle Applications Including Cost Consideration. Energies. 2019; 12(22):4272. https://doi.org/10.3390/en12224272
Chicago/Turabian StyleRoemer, Felix, Massab Ahmad, Fengqi Chang, and Markus Lienkamp. 2019. "Optimization of a Cascaded H-Bridge Inverter for Electric Vehicle Applications Including Cost Consideration" Energies 12, no. 22: 4272. https://doi.org/10.3390/en12224272
APA StyleRoemer, F., Ahmad, M., Chang, F., & Lienkamp, M. (2019). Optimization of a Cascaded H-Bridge Inverter for Electric Vehicle Applications Including Cost Consideration. Energies, 12(22), 4272. https://doi.org/10.3390/en12224272