An Orderly Power Utilization Scheme Based on an Intelligent Multi-Agent Apanage Management System
Abstract
:1. Introduction
- (1)
- The initiative IMAS can achieve coordinated optimization within the jurisdiction, make decisions and adjustments to the power usage plan, and improve the efficiency of information transmission;
- (2)
- The proposed MAM can participate in the adjustment of the OPU plan, realize the mutual coordination between users, improve the user’s interactive ability and establish a aid order table to ensure the fairness of electricity consumption;
- (3)
- The proposed I-CFSFDP algorithm can effectively reduce the difficulty of modeling and solving, and can fully consider its time based on uncertain modeling of electricity consumption behavior;
- (4)
- The established multi-objective OPU decision model comprehensively considers the interests of both users and the grid, users’ willingness and taps the potential of users. FSS is used to solve the proposed model. It is verified by the load data from the Open Energy Information (Open EI) website of the U.S. Department of Energy [26]. The results show that the model is reasonable and the algorithm is effective. Definition of nomenclature are showed in Table 1.
2. IMAS for OPU
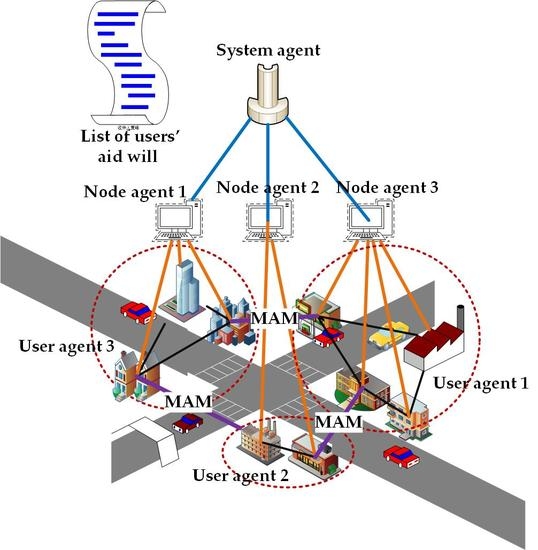
2.1. System Architecture
- (1)
- The system agent is responsible for calculating the system gap index. First, it collects the energy-saving characteristics of the subordinate nodes (including energy-saving potential and energy-saving loss coefficient) from each node agent. Then, according to the energy-saving characteristics, it calls the orderly allocation algorithm of the power gap index. Finally, the gap index is allocated to each node agent.
- (2)
- First, the node agent reports energy-saving characteristics to the system agent. Secondly, after getting the allocated gap indicators from the system agent, the node agent collects the energy-saving characteristics from the subordinate user agents and then, assigns the gap indicators to the user agents.
- (3)
- The user agents are the lowest layers in a IMAS. It abstracts the user and collects the user’s energy-saving features and reports them to the node agent.
- (4)
- In the interactive module, the negotiation agent first collects the aid willingness of users to form a list. When a user is unable to perform the tasks as planned, the user agent can issue an aid request on the interactive platform. After querying the request, the negotiation agent quickly adjusts the OPU plan according to the user’s aid willingness table. Then the agent updates the table according to the aid situation to ensure the fairness of electricity consumption.
2.2. Indicator Distribution Mechanism
- (1)
- Each layer of agent reports the energy-saving feature to the upper layer agent, and the upper layer agent summarizes the equivalent energy-saving characteristics;
- (2)
- After obtaining the energy-saving characteristics of the lower layer agent, the upper layer agent completes the gap index assignment task from the upper level to the lower level according to the allocated OPU gap indicator.
3. I-CFSFDP
3.1. CFSFDP Algorithm
3.2. I-CFSFDP Algorithm
3.2.1. KNN Algorithms and Their k-d Tree Implementation
3.2.2. Principal Component Analysis for Dimension Reduction
3.3. Improvement of the CFSFDP Algorithm
- (1)
- The local sample density of the dataset is sorted in descending order and set to , , so that i = 2.
- (2)
- Calculate the distance of density according to Equation (5), i = i + 1.
- (3)
- If i n, return to step (2); otherwise, i = 1. The distance corresponding to the density is calculated according to Equation (6).
3.4. I-CFSFDP Algorithm Step
- (1)
- The dataset X is normalized. This treatment fully reflects the morphological characteristics of each load curve, avoiding the influence of dimension and amplitude difference on the load curve clustering.
- (2)
- The normalized dataset is dimensionally reduced by PCA to ;
- (3)
- The KNN matrix of is established by the k-d tree algorithm.
- (4)
- Calculate the and of samples according to Equations (4)–(7);
- (5)
- Since the difference between the order of magnitude and makes the weights of the two different, the first and are normalized, and the resulting decision curve avoids this problem. The larger point is selected as the cluster center.
- (6)
- The remaining samples are assigned, and each sample belongs to the same category as the denser and closest sample.
4. OPU Model Considering DSM
4.1. Establishment of Objective Function Model
4.2. Load Regulation Model
4.3. Modeling of Household PV Generation Devices
4.4. Modeling of EV
4.5. User Load Curve after OPU
4.6. Constraints Condition
- (1)
- Maximum output constraints of the system
- (2)
- Constraints of peak shifting and peak clippingThe number of hours of the peak staggering should not exceed and and the peak clipping level should not exceed the maximum tolerable level .
- (3)
- Peak avoidance constraintEach user uses at most one peak avoidance method one day.In the formula, takes 1 to indicate that i-user participates in peak shifting on k-day; takes 0 to indicate i-user participates in peak shifting and valley filling on k-day; takes 1 to indicate i-user participates in peak clipping on k-day; takes 0 to indicate that i-user participates in peak shifting on k-day as a rest day.
- (4)
- The constraint of peak rotatingdenotes the number of working days one week for the user. The above formula means that the total number of working days per user a week is fixed. Usually, .
- (5)
- Daily participation restriction.The meaning of the Formula (30) is that each user can only participate in one peak avoidance mode every day.
4.7. Solution Algorithm
4.8. Adjustment of OPU Scheme
5. Examples and Analysis of Planning Results
5.1. Scenario 1: In the First Week, the Region Was Allocated to Eliminate 10% of the Power Supply Gap, and the OPU Decision-Making Scheme in this Study Was Analyzed
5.2. Scenario 2: In the Process of Implementation, the User Needs to be Aided
5.3. Comparison of Algorithm
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| OPU | orderly power utilization | KNN | k-nearest neighbors |
| EV | electric vehicle | IMAS | intelligent multi-agent system |
| CFSFDP | clustering by fast search and find of density peaks | I-CFSFDP | improved clustering by fast search and find of density peaks |
| FSS | forbearing stratified sequencing | MAM | mutual aid mechanism |
| M2OM | multi-objective optimization model | Open EI | Open Energy Information |
| PV | photovoltaic | PCA | principal component analysis |
| DSM | demand-side management | DSR | demand-side resources |
References
- Gellings, C.W. Evolving practice of demand-side management. J. Mod. Power Syst. Clean Energy 2017, 5, 1–9. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand Side Management: Demand Response, Intelligent Energy Systems, and Smart Loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Su, C.L.; Kirschen, D. Quantifying the effect of demand response on electricity markets. IEEE Trans. Power Syst. 2009, 24, 1199–1207. [Google Scholar]
- Ahmed, N.; Levorato, M.; Li, G.P. Residential Consumer-Centric Demand Side Management. IEEE Trans. Smart Grid 2017, 9, 4513–4524. [Google Scholar] [CrossRef]
- Han, S.; Han, S.; Sezaki, K. Development of an Optimal Vehicle-to-Grid Aggregator for Frequency Regulation. IEEE Trans. Smart Grid 2010, 1, 65–72. [Google Scholar]
- Xiao, X.; Min, P.; Si, L. A Personalized Orderly Charging Strategy for Electric Vehicles Considering Users’ Needs. In Proceedings of the IEEE International Conference on Power System Technology, Guangzhou, China, 6–8 November 2018. [Google Scholar]
- Hamed, S.G.; Kazemi, A. Multi-objective cost-load optimization for demand side management of a residential area in smart grids. Sustain. Cities Soc. 2017, 32, 171–180. [Google Scholar]
- Chavali, P.; Yang, P.; Nehorai, A. A Distributed Algorithm of Appliance Scheduling for Home Energy Management System. IEEE Trans. Smart Grid 2014, 5, 282–290. [Google Scholar] [CrossRef]
- Hadian, A.; Haghifam, M.R.; Zohrevand, J.; Akhavan-Rezai, E. Probabilistic approach for renewable DG placement in distribution systems with uncertain and time varying loads. In Proceedings of the IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Zeng, B.; Zhang, J.H.; Yang, X.; Wang, J.H.; Dong, J.; Zhang, Y.Y. Intergrated planning for transition to low-carbon distribution systems with renewable energy generation and demand response. IEEE Trans. Power Syst. 2014, 29, 1153–1165. [Google Scholar] [CrossRef]
- Kaloudas, C.G.; Ochoa, L.F.; Marshall, B.; Majithia, S.; Fletcher, I. Assessing the feature trends of reactive power demand of distribution networks. IEEE Trans. Power Syst. 2017, 32, 4278–4288. [Google Scholar] [CrossRef]
- Shen, X.W.; Shahidehpour, M.; Zhu, S.Z.; Han, Y.D.; Zheng, J.H. Multi-stage planning of active distribution networks considering the co-optimization of operation strategies. IEEE Trans. Smart Grid 2018, 9, 1425–1433. [Google Scholar] [CrossRef]
- Chicco, G.; Napoli, R.; Piglione, F. Comparisons Among Clustering Techniques for Electricity Customer Classification. IEEE Trans. Power Syst. 2006, 21, 933–940. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Azzag, H.; Venturini, G.; Oliver, A. A hierarchical ant based clustering algorithm and its use in three real-world applications. Eur. J. Oper. Res. 2007, 179, 906–922. [Google Scholar] [CrossRef]
- He, Y.; Tan, H.; Luo, W. MR-DBSCAN: An Efficient Parallel Density-based Clustering Algorithm using MapReduce. In Proceedings of the IEEE International Conference on Parallel & Distributed Systems, Singapore, 17–19 December 2012. [Google Scholar]
- Rodriguez, A.; Laio, A. Machine learning. Clustering by fast search and find of density peaks. Science 2014, 344, 1492. [Google Scholar] [CrossRef] [PubMed]
- Pilevar, A.H.; Sukumar, M. GCHL: A grid-clustering algorithm for high-dimensional very large spatial data bases. Pattern Recognit. Lett. 2005, 26, 999–1010. [Google Scholar] [CrossRef]
- Zhang, Y.; Brady, M.; Smith, S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans. Med. Imaging 2002, 20, 45–57. [Google Scholar] [CrossRef]
- Davidson, E.M.; Mcarthur, S.D.J.; Mcdonald, J.R. Applying multi-agent system technology in practice: Automated management and analysis of SCADA and digital fault recorder data. IEEE Trans. Power Syst. 2006, 21, 559–567. [Google Scholar] [CrossRef]
- Li, W.; Logenthiran, T.; Phan, V.-T.; Woo, W.L. Intelligent Multi-Agent System for Power Grid Communication. In Proceedings of the IEEE TENCON 2016-2016 IEEE Region 10 Conference, Singapore, 22–25 November 2016. [Google Scholar]
- Wilkosz, K. Utilization of multi-agent system for power system topology verification. In Proceedings of the IEEE 2014 15th International Scientific Conference on Electric Power Engineering (EPE), Brno-Bystrc, Czech Republic, 12–14 May 2014. [Google Scholar]
- Deng, R.; Yang, Z.; Chow, M.Y. A Survey on Demand Response in Smart Grids: Mathematical Models and Approaches. IEEE Trans. Ind. Inform. 2015, 11, 570–582. [Google Scholar] [CrossRef]
- Farid, A.M. Multi-Agent System Design Principles for Resilient Coordination & Control of Future Power Systems. Intell. Ind. Syst. 2015, 1, 255–269. [Google Scholar]
- Multazam, T.; Putri, R.I.; Pujiantara, M. Wind farm Site Selection Base On Fuzzy Analytic Hierarchy Process Method; Case Study Area Nganjuk. In Proceedings of the International Seminar on Intelligent Technology and Its Applications (ISITIA), Mataram, Indonesia, 28–30 July 2016. [Google Scholar]
- Commercial and Residential Hourly Load Profiles for all TMY3 Locations in the United States. Available online: https://openei.org/doe-opendata/dataset/commercial-and-residential-hourly-load-profiles-for-all-tmy3-locations-in-the-united-states (accessed on 1 September 2014).
- Wang, S.; Wang, D.; Li, C. Comment on “Clustering by fast search and find of density peaks”. arXiv 2015, arXiv:1501.04267. [Google Scholar]
- Du, M.; Ding, S.; Jia, H. Study on Density Peaks Clustering Based on k-Nearest Neighbors and Principal Component Analysis. Knowl. Based Syst. 2016, 99, 135–145. [Google Scholar] [CrossRef]
- Duch, A.; Jiménez, R.M.; Martínez, C. Selection by rank in K-dimensional binary search trees. Random Struct. Algorithms 2014, 45, 14–37. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1953, 13, 21–27. [Google Scholar] [CrossRef]
- Kambhatla, N.; Leen, T.K. Dimension Reduction by Local Principal Component Analysis. Neural Comput. 1997, 9, 1493–1516. [Google Scholar] [CrossRef]
- Baldi, P.; Hornik, K. Neural networks and principal component analysis: Learning from examples without local minima. Neural Netw. 1989, 2, 53–58. [Google Scholar] [CrossRef]
- Tipping, M.E.; Bishop, C.M. Probabilistic Principal Component Analysis. J. R. Stat. Soc. 2010, 61, 611–622. [Google Scholar] [CrossRef]
- Nomikos, P.; Macgregor, J.F. Monitoring batch processes using multiway principal component analysis. Aiche J. 2010, 40, 1361–1375. [Google Scholar] [CrossRef]
- Bie, R.; Mehmood, R.; Ruan, S. Adaptive fuzzy clustering by fast search and find of density peaks. Pers. Ubiquitous Comput. 2016, 20, 785–793. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, M.; Zheng, J. Optimization of clustering by fast search and find of density peaks. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Kansas City, MO, USA, 13–16 November 2017. [Google Scholar]
- Wang, J.; Neskovic, P.; Cooper, L.N. Improving nearest neighbor rule with a simple adaptive distance measure. Pattern Recognit. Lett. 2007, 28, 207–213. [Google Scholar] [CrossRef]
- Jégou, H.; Douze, M.; Schmid, C. Product Quantization for Nearest Neighbor Search. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 117–128. [Google Scholar] [CrossRef]
- Pasetti, M.; Rinaldi, S.; Flammini, A. Assessment of Electric Vehicle Charging Costs in Presence of Distributed Photovoltaic Generation and Variable Electricity Tariffs. Energies 2019, 12, 499. [Google Scholar] [CrossRef]
- Richardson, P.; Flynn, D.; Keane, A. Optimal Charging of Electric Vehicles in Low-Voltage Distribution Systems. IEEE Trans. Power Syst. 2012, 27, 268–279. [Google Scholar] [CrossRef]
- Babich, O.A.; Pershin, O.Y.; Mushtonin, A.V. A Method to Design a Hierarchical Network of Field Pipelines by Solving a Sequence of Extremal Problems. Autom. Remote Control 2003, 64, 806–814. [Google Scholar] [CrossRef]
- Song, Y.; Morency, L.P.; Davis, R. Action Recognition by Hierarchical Sequence Summarization. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Columbus, OH, USA, 24–27 June 2014. [Google Scholar]










| Nomenclature | |||
|---|---|---|---|
| distance between sample i and j (Euclidean distance) | control cost coefficient of peak clipping | ||
| truncation distance | peak clipping grade | ||
| whole data set | PV conversion rate | ||
| recipient capacity | contact area of the battery plate | ||
| historical aid score. | light radiation intensity | ||
| recipient capacity matrix | number of the battery plates | ||
| m | number of recipient users | external environment temperature. | |
| aid capacity matrix | charging power of the EV in t-period | ||
| n | number of aid users | rated charging power | |
| local density of each sample | charging state, and 1 means charging | ||
| local distance of each sample | charging state of the battery in t-period | ||
| KNN (i) | KNN sample set of sample i | charging state of the battery | |
| loads at the time t | maximum power supply on the k-day | ||
| values at the time t after normalization of the load curve | , , | maximum/minimum tolerable hours | |
| total number of users | Y | aid user set | |
| total number of residents | price of different periods in a day | ||
| daily maximum/minimum load | a load of users in the k-day t-period after OPU | ||
| number of users with weekly rest | value score of i-user |
| Time (h) | Electricity Price/($/(kW·h)) |
|---|---|
| Valley time (0:00–7:00, 22:00–24:00) | 0.051 |
| Peak period (7:00–9:00, 14:00–16:00, 18:00–20:00) | 0.13 |
| Ordinary hours (9:00–14:00, 16:00–18:00, 20:00–22:00) | 0.0977 |
| User | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
|---|---|---|---|---|---|---|---|
| 1 | 2 h | 1 h | -- | -- | rest | rest | -- |
| 2 | rest | -- | -- | -- | -- | rest | -- |
| 3 | 1 h | rest | -- | -- | -- | -- | rest |
| 4 | −2 h | -- | -- | −1 h | rest | -- | rest |
| 5 | -- | -- | -- | -- | -- | rest | rest |
| 6 | -- | - | rest | -- | -- | rest | -- |
| Program | User | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
|---|---|---|---|---|---|---|---|---|
| Before adjustment | 1 | -- | -- | 1 | -- | rest | rest | -- |
| 5 | -- | -- | -- | -- | -- | rest | rest | |
| After adjustment | 1 | -- | -- | -- | -- | -- | rest | rest |
| 5 | -- | -- | -- | rest | -- | rest |
| User | Number of Aid for this Method | Number of Aid from Traditional Methods |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 0 |
| 3 | 1 | 2 |
| 4 | 1 | 5 |
| 5 | 2 | 0 |
| 6 | 1 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, R.; Zuo, D.; Zhang, X.; Sun, W. An Orderly Power Utilization Scheme Based on an Intelligent Multi-Agent Apanage Management System. Energies 2019, 12, 4563. https://doi.org/10.3390/en12234563
Jin R, Zuo D, Zhang X, Sun W. An Orderly Power Utilization Scheme Based on an Intelligent Multi-Agent Apanage Management System. Energies. 2019; 12(23):4563. https://doi.org/10.3390/en12234563
Chicago/Turabian StyleJin, Ruijiu, Dongsheng Zuo, Xiangfeng Zhang, and Wengang Sun. 2019. "An Orderly Power Utilization Scheme Based on an Intelligent Multi-Agent Apanage Management System" Energies 12, no. 23: 4563. https://doi.org/10.3390/en12234563
APA StyleJin, R., Zuo, D., Zhang, X., & Sun, W. (2019). An Orderly Power Utilization Scheme Based on an Intelligent Multi-Agent Apanage Management System. Energies, 12(23), 4563. https://doi.org/10.3390/en12234563