Prediction of the Energy Consumption Variation Trend in South Africa based on ARIMA, NGM and NGM-ARIMA Models
Abstract
:1. Introduction
2. Research Method and Data Source
2.1. Research Method
2.1.1. ARIMA Prediction Model
2.1.2. NGM Prediction Model
2.1.3. NGM-ARIMA Prediction Model
2.1.4. Characteristics and Limitations of Each Model
2.2. Data Source
3. Empirical Results and Discussion
3.1. Operation Process of the Three Models
3.1.1. ARIMA Model Fitting Process
3.1.2. NGM Model Fitting Process
3.1.3. NGM-ARIMA Model Fitting Process
3.2. Model Goodness Inspection
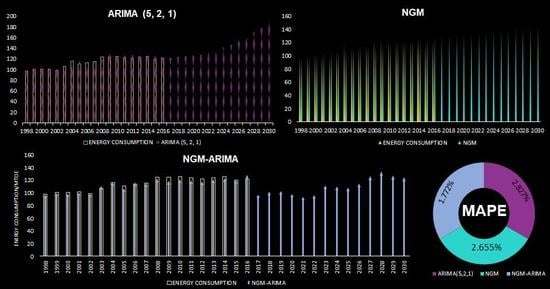
3.3. Prediction Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dudley, B. Statistical Review of World Energy; BP Statistical Review: London, UK, 2018. [Google Scholar]
- Ebohon, O.J. Energy, economic growth and causality in developing countries: A case study of Tanzania and Nigeria. Energy Policy 2007, 24, 447–453. [Google Scholar] [CrossRef]
- Gessner, U.; Knauer, K.; Machwitz, M.; Dech, S.; Kuenzer, C. Impacts of Socio-economic Development and Urbanization on Natural Resources-Case Studies from Africa. In Proceedings of the Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016. [Google Scholar]
- Oyedepo, S.O. On energy for sustainable development in Nigeria. Renew. Sustain. Energy Rev. 2012, 16, 2583–2598. [Google Scholar] [CrossRef]
- Adom, P.K.; Bekoe, W. Conditional dynamic forecast of electrical energy consumption requirements in Ghana by 2020: A comparison of ARDL and PAM. Energy 2012, 44, 367–380. [Google Scholar] [CrossRef]
- Bazilian, M.; Nussbaumer, P.; Rogner, H.H.; Brew-Hammond, A.; Foster, V.; Pachauri, S.; Williams, E.; Howells, M.; Niyongabo, P.; Musaba, L.; et al. Energy access scenarios to 2030 for the power sector in sub-Saharan Africa. Util. Policy 2012, 20, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Mentis, D.; Hermann, S.; Howells, M.; Welsch, M.; Siyal, S.H. Assessing the technical wind energy potential in Africa a GIS-based approach. Renew. Energy 2015, 83, 110–125. [Google Scholar] [CrossRef]
- Sigauke, C.; Chikobvu, D. Prediction of daily peak electricity demand in South Africa using volatility forecasting models. Energy Econ. 2011, 33, 882–888. [Google Scholar] [CrossRef]
- Thopil, G.A.; Pouris, A. A 20 year forecast of water usage in electricity generation for South Africa amidst water scarce conditions. Renew. Sustain. Energy Rev. 2016, 62, 1106–1121. [Google Scholar] [CrossRef] [Green Version]
- Tsikata, M.; Sebitosi, A.B. Struggling to wean a society away from a century-old legacy of coal based power: Challenges and possibilities for South African Electric supply future. Energy 2010, 35, 1281–1288. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Jimoh, A.A.; Munda, J.L.; Agee, J.T. A Statistical Analysis of Wind Distribution and Wind Power Potential in the Coastal Region of South Africa. Int. J. Green Energ. 2013, 10, 814–834. [Google Scholar] [CrossRef]
- Walwyn, D.R.; Brent, A.C. Renewable energy gathers steam in South Africa. Renew. Sustain. Energy Rev. 2015, 41, 390–401. [Google Scholar] [CrossRef] [Green Version]
- Malondkar, A.; Corizzo, R.; Kiringa, I.; Ceci, M.; Japkowicz, N. Spark-GHSOM: Growing Hierarchical Self-Organizing Map for large scale mixed attribute datasets. Inf. Sci. 2019, 496, 572–591. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O. Prediction of wind speed for the estimation of wind turbine power output from site climatological data using artificial neural network. Int. J. Ambient. Energy 2015, 38, 29–36. [Google Scholar] [CrossRef]
- Sotomane, C.; Asker, L.; Boström, H.; Massingue, V. Short-term Forecasting of Electricity Consumption in Maputo. In Proceedings of the International Conference on Advances in ICT for Emerging Regions. (ICTer), Colombo, Sri Lanka, 11–15 December 2013; pp. 132–136. [Google Scholar]
- Inglesi, R. Aggregate electricity demand in South Africa: Conditional forecasts to 2030. Appl. Energy 2010, 87, 197–204. [Google Scholar] [CrossRef] [Green Version]
- Ahjum, F.; Merven, B.; Cullis, J.; Goldstein, G.; DeLaquil, P.; Stone, A. Development of a national water-energy system model with emphasis on the power sector for south africa. Environ. Prog. Sustain. Energy 2018, 37, 132–147. [Google Scholar] [CrossRef]
- Fadare, D.A. Modelling of solar energy potential in Nigeria using an artificial neural network model. Appl. Energy 2009, 86, 1410–1422. [Google Scholar] [CrossRef]
- Bessa, R.J.; Trindade, A.; Miranda, V. Spatial-temporal solar power forecasting for smart grids. IEEE Trans. Ind. Inform. 2014, 11, 232–241. [Google Scholar] [CrossRef]
- Ceci, M.; Corizzo, R.; Malerba, D.; Rashkovska, A. Spatial autocorrelation and entropy for renewable energy forecasting. Data Min. Knowl. Discov. 2019, 33, 698–729. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Li, R. China’s Dependency on Foreign Oil Will Exceed 80% by 2030: Developing a Novel NMGM-ARIMA to Forecast China’s Foreign Oil Dependence from Two Dimensions. Energy 2018, 163, 151–167. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Li, R. Forecasting Energy Demand in China and India: Using Single-linear, Hybrid-linear, and Non-linear Time Series Forecast Techniques. Energy 2018, 161, 821–831. [Google Scholar] [CrossRef]
- Bartholomew, D.J. Time Series Analysis Forecasting and Control. J. Oper. Res. Soc. 1971, 22, 199–201. [Google Scholar] [CrossRef]
- Ramakrishna, G.; Kumari, R.V. Arima Model for Forecasting of Rice Production in India by Using Sas. Siam J. Appl. Math. 2018, 6, 67–72. [Google Scholar]
- Sen, P.; Roy, M.; Pal, P. Application of ARIMA for forecasting energy consumption and GHG emission: A case study of an Indian pig iron manufacturing organization. Energy 2016, 116, 1031–1038. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, S. An optimized grey model for annual power load forecasting. Energy 2016, 107, 272–286. [Google Scholar] [CrossRef]
- Li, S.; Li, R. Comparison of forecasting energy consumption in Shandong, China Using the ARIMA model, GM model, and ARIMA-GM model. Sustainability 2017, 9, 1181. [Google Scholar]
- Yuan, C.; Liu, S.; Fang, Z. Comparison of China’s primary energy consumption forecasting by using ARIMA (the autoregressive integrated moving average) model and GM (1, 1) model. Energy 2016, 100, 384–390. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Z.; Snowling, S.; Siam, A.; El-Dakhakhni, W. Predictive models for wastewater flow forecasting based on time series analysis and artificial neural network. Water Sci. Technol. 2019, 80, 243–253. [Google Scholar] [CrossRef]
- Lu, B.; Zhao, S.; Tian, Y.; Yang, Y.; Li, B.; Chen, X. Mid-long term electricity consumption forecasting based on improved NGM (1, 1, k) gray model. Power Syst. Prot. Control 2015, 43, 98–103. [Google Scholar]
- Du, Y.; Liang, W.; Wang, H.; Hua, W. Coal consumption forecast in anhui province-based on GM (1, 1). J. Tonghua Normal Univ. 2016, 37, 25–26. [Google Scholar]
- Guo, X.; Liu, S.; Wu, L.; Tang, L. A grey NGM (1, 1, k) self-memory coupling prediction model for energy consumption prediction. Sci. World J. 2014, 2014, 327. [Google Scholar] [CrossRef]
- Wang, Z.X. Nonlinear Grey Prediction Model with Convolution Integral NGMC (1, n) and Its Application to the Forecasting of China’s Industrial SO2 Emissions. J. Appl. Math. 2014, 2014, 174–178. [Google Scholar]
- Ren, S.; Chan, H.L.; Ram, P. A Comparative Study on Fashion Demand Forecasting Models with Multiple Sources of Uncertainty. Ann. Oper. Res. 2016, 257, 1–21. [Google Scholar] [CrossRef]
- Boyd, G.; Na, D.; Li, Z.; Snowling, S.; Zhang, Q.; Zhou, P. Influent Forecasting for Wastewater Treatment Plants in North America. Sustainability 2019, 11, 1764. [Google Scholar] [CrossRef] [Green Version]
- Khair, U.; Fahmi, H.; Al Hakim, S.; Rahim, R. Forecasting Error Calculation with Mean Absolute Deviation and Mean Absolute Percentage Error. J. Phys. Conf. Ser. IOP Publ. 2017, 930, 012002. [Google Scholar] [CrossRef]
- Odhiambo, N.M. Savings and economic growth in South Africa: A multivariate causality test. J. Policy Model. 2009, 31, 708–718. [Google Scholar] [CrossRef]







| Augmented Dickey–Fuller | Confidence Level | t-Statistic | Probability * |
|---|---|---|---|
| Test statistic | 3.639257 | 0.0665 | |
| Test critical values | 1% level | 4.886426 | |
| 5% level | 3.828975 | ||
| 10% level | 3.362984 |
| Model | Number of Predictors | Model Fit Statistics | Number of Outliers |
|---|---|---|---|
| Stationary R2 | |||
| ARIMA (5,2,1) | 1 | 0.523 | 0 |
| Year | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| Power coefficient | 1 | 1 | 1 | 1 | 0.001 | 0.001 | 0.571 | 1 |
| Year | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | |
| Power coefficient | 1 | 1 | 1 | 1 | 0.001 | 0.934 | 1 |
| Year | MAPE | MSPE | MSE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ARIMA | NGM | NGM-ARIMA | ARIMA | NGM | NGM-ARIMA | ARIMA | NGM | NGM-ARIMA | |
| 1998 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 1.0000 | 1.0000 |
| 1999 | 0.0000 | 0.0140 | 0.0066 | 0.0000 | 0.0002 | 0.0000 | 1.0000 | 0.9997 | 0.9999 |
| 2000 | 0.0262 | 0.0126 | 0.0183 | 0.0007 | 0.0002 | 0.0003 | 0.9995 | 0.9998 | 0.9996 |
| 2001 | 0.0024 | 0.0312 | 0.0021 | 0.0000 | 0.0010 | 0.0000 | 1.0000 | 0.9994 | 1.0000 |
| 2002 | 0.0300 | 0.0819 | 0.0099 | 0.0009 | 0.0067 | 0.0001 | 0.9994 | 0.9983 | 0.9998 |
| 2003 | 0.0853 | 0.0151 | 0.0391 | 0.0073 | 0.0002 | 0.0015 | 0.9984 | 0.9997 | 0.9993 |
| 2004 | 0.0847 | 0.0536 | 0.0072 | 0.0072 | 0.0029 | 0.0001 | 0.9985 | 0.9991 | 0.9999 |
| 2005 | 0.0479 | 0.0148 | 0.0218 | 0.0023 | 0.0002 | 0.0005 | 0.9991 | 0.9997 | 0.9996 |
| 2006 | 0.0294 | 0.0052 | 0.0345 | 0.0009 | 0.0000 | 0.0012 | 0.9995 | 0.9999 | 0.9994 |
| 2007 | 0.0114 | 0.0000 | 0.0047 | 0.0001 | 0.0000 | 0.0000 | 0.9998 | 1.0000 | 0.9999 |
| 2008 | 0.0419 | 0.0604 | 0.0078 | 0.0018 | 0.0036 | 0.0001 | 0.9993 | 0.9990 | 0.9999 |
| 2009 | 0.0333 | 0.0475 | 0.0396 | 0.0011 | 0.0023 | 0.0016 | 0.9995 | 0.9992 | 0.9994 |
| 2010 | 0.0191 | 0.0436 | 0.0228 | 0.0004 | 0.0019 | 0.0005 | 0.9997 | 0.9993 | 0.9996 |
| 2011 | 0.0271 | 0.0193 | 0.0243 | 0.0007 | 0.0004 | 0.0006 | 0.9996 | 0.9997 | 0.9996 |
| 2012 | 0.0465 | 0.0052 | 0.0227 | 0.0022 | 0.0000 | 0.0005 | 0.9992 | 0.9999 | 0.9996 |
| 2013 | 0.0067 | 0.0022 | 0.0054 | 0.0000 | 0.0000 | 0.0000 | 0.9999 | 1.0000 | 0.9999 |
| 2014 | 0.0067 | 0.0006 | 0.0051 | 0.0000 | 0.0000 | 0.0000 | 0.9999 | 1.0000 | 0.9999 |
| 2015 | 0.0311 | 0.0527 | 0.0122 | 0.0010 | 0.0028 | 0.0001 | 0.9995 | 0.9991 | 0.9998 |
| 2016 | 0.0071 | 0.0443 | 0.0527 | 0.0001 | 0.0020 | 0.0028 | 0.9999 | 0.9993 | 0.9991 |
| Average | 0.0283 | 0.0265 | 0.0177 | 0.0086 | 0.0082 | 0.0053 | 0.9995 | 0.9995 | 0.9997 |
| YEAR | ARIMA (5, 2, 1) | NGM | NGM-ARIMA |
|---|---|---|---|
| 2017 | 121.6615 | 128.9256 | 97.7957 |
| 2018 | 124.5612 | 130.1407 | 102.4731 |
| 2019 | 125.1492 | 131.3387 | 103.3278 |
| 2020 | 126.6525 | 132.5208 | 98.5698 |
| 2021 | 128.3105 | 133.6881 | 93.6602 |
| 2022 | 133.1727 | 134.8415 | 96.3183 |
| 2023 | 136.0278 | 135.982 | 112.6159 |
| 2024 | 142.0273 | 137.1102 | 110.6475 |
| 2025 | 145.8276 | 138.2269 | 108.5081 |
| 2026 | 153.6211 | 139.3328 | 115.2856 |
| 2027 | 160.2464 | 140.4284 | 127.6118 |
| 2028 | 169.8985 | 141.5143 | 134.5952 |
| 2029 | 178.2913 | 142.5909 | 128.2806 |
| 2030 | 190.0362 | 143.6588 | 125.6522 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, M.; Wang, Z. Prediction of the Energy Consumption Variation Trend in South Africa based on ARIMA, NGM and NGM-ARIMA Models. Energies 2020, 13, 10. https://doi.org/10.3390/en13010010
Ma M, Wang Z. Prediction of the Energy Consumption Variation Trend in South Africa based on ARIMA, NGM and NGM-ARIMA Models. Energies. 2020; 13(1):10. https://doi.org/10.3390/en13010010
Chicago/Turabian StyleMa, Minglu, and Zhuangzhuang Wang. 2020. "Prediction of the Energy Consumption Variation Trend in South Africa based on ARIMA, NGM and NGM-ARIMA Models" Energies 13, no. 1: 10. https://doi.org/10.3390/en13010010
APA StyleMa, M., & Wang, Z. (2020). Prediction of the Energy Consumption Variation Trend in South Africa based on ARIMA, NGM and NGM-ARIMA Models. Energies, 13(1), 10. https://doi.org/10.3390/en13010010