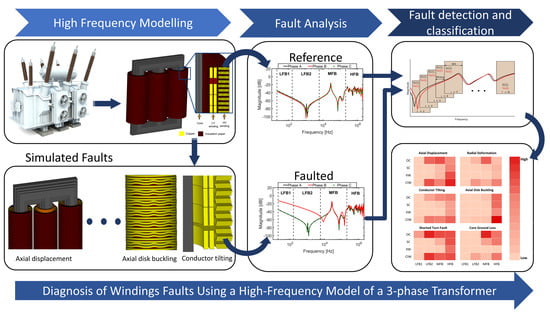
A Comprehensive Analysis of Windings Electrical and Mechanical Faults Using a High-Frequency Model
Abstract
:1. Introduction
2. Principle of FRA
3. High-Frequency Transformer Modelling
4. Validation of 3D HF Transformer Model
5. Evaluation Method
5.1. Transformer Winding Assessment Algorithm
- Increased fault detectability;
- Removes the issue of fixed frequency sub-bands for FRA interpretation;
- Plotting deviation between two TFs as a function of frequency;
- Possibility to set a threshold to the lowest value of SDD function, i.e., MSDD;
- Possibility of faults classification.
5.2. Division of Frequency Sub-Bands for Fault Classification
6. Fault Mechanism in Transformer Windings
6.1. Mechanical Failure Modes
6.1.1. Axial Displacement Fault (ADF)
6.1.2. Radial Deformation Fault (RDF)
6.1.3. Conductor Tilting Fault (CTF)
6.1.4. Axial Disk Buckling Fault (ADBF)
6.2. Electrical Faults
6.2.1. Turn-To-Turn Short Circuit Fault (TSCF)
6.2.2. Missing Core Ground Fault (MCGF)
7. Future Work
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Details |
|---|---|
| LV winding | Layer winding: 24 turns, 12 parallel conductors in each turn |
| HV winding | Disc winding: 60 discs, 11 turns in each disc |
| Radius of core | 10.5 cm |
| Inner radius of LV | 11.5 cm |
| Inner radius of HV | 14.57 cm |
| Height of core | 134 cm |
| Windings height | 85 cm |
| Tank height | 136 cm |
| Tank width | 52.8 cm |
| Tank length | 132 cm |
| Employed vector group | YNyn0 |
References
- Transformer Reliability Survey; CIGRÉ A2.37; Vol. Technical Brochure 642; CIGRÉ: Paris, France, 2015; ISBN 978-2-85873-346-0.
- Tenbohlen, S.; Coenen, S.; Djamali, M.; Müller, A.; Samimi, M.; Siegel, M. Diagnostic Measurements for Power Transformers. Energies 2016, 9, 347. [Google Scholar] [CrossRef]
- Van Bolhuis, J.P.; Gulski, E.; Smit, J.J. Monitoring and Diagnostic of Transformer Solid Insulation. IEEE Trans. Power Deliv. 2002, 17, 528–536. [Google Scholar] [CrossRef]
- Rahimpour, E.; Christian, J.; Feser, K.; Mohseni, H. Transfer Function Method to Diagnose Axial Displacement and Radial Deformation of Transformer Windings. IEEE Trans. Power Deliv. 2003, 18, 493–505. [Google Scholar] [CrossRef]
- Christian, J.; Feser, K. Procedures for Detecting Winding Displacements in Power Transformers by the Transfer Function Method. IEEE Trans. Power Deliv. 2004, 19, 214–220. [Google Scholar] [CrossRef]
- Miyazaki, S.; Tahir, M.; Tenbohlen, S. Detection and Quantitative Diagnosis of Axial Displacement of Transformer Winding by Frequency Response Analysis. IET Gener. Transm. Distrib. 2019, 13, 3493–3500. [Google Scholar] [CrossRef]
- Rahimpour, E.; Jabbari, M.; Tenbohlen, S. Mathematical Comparison Methods to Assess Transfer Functions of Transformers to Detect Different Types of Mechanical Faults. IEEE Trans. Power Deliv. 2010, 25, 2544–2555. [Google Scholar] [CrossRef]
- IEEE Guide for the Application and Interpretation of Frequency Response Analysis for Oil-Immersed Transformers; IEEE Std. C57.149-2012; IEEE Standard Association: New York, NY, USA, 2013.
- Measurement of Frequency Response, ED. 1’; IEC60076-18; IEC Std.: Geneva, Switzerland, 2012.
- Picher, P.; Tenbohlen, S.; Lachman, M.; Scardazzi, A.; Patel, P. Current State of Transformer FRA Interpretation. Procedia Eng. 2017, 202, 3–12. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, S.; Yuan, D.; Tao, X. Double-Ladder Circuit Model of Transformer Winding for Frequency Response Analysis Considering Frequency-Dependent Losses. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Larin, V.S.; Matveev, D.A. Analysis of Transformer Frequency Response Deviations Using White-Box Modelling; CIGRE: Cracow, Poland, 2017. [Google Scholar]
- Abed, N.Y.; Mohammed, O.A. Physics-Based High-Frequency Transformer Modeling by Finite Elements. IEEE Trans. Magn. 2010, 46, 3249–3252. [Google Scholar] [CrossRef]
- Samimi, M.H.; Tenbohlen, S. FRA Interpretation Using Numerical Indices: State-Of-The-Art. Int. J. Electr. Power Energy Syst. 2017, 89, 115–125. [Google Scholar] [CrossRef]
- Weiland, T. A Discretization Method for the Solution of Maxwell’s Equations for Six-Component Fields. Electron. Commun. AEU 1977, 31, 116–120. [Google Scholar]
- CST MICROWAVE STUDIO® 5 User’s Manual. Available online: www.cst.com (accessed on 24 December 2019).
- Kulkarni, S.V.; Khaparde, S.A. Transformer Engineering: Design and Practice; Power Engineering; Marcel Dekker, Inc.: New York, NY, USA, 2004; ISBN 978-0-8247-5653-6. [Google Scholar]
- Reykherdt, A.A.; Davydov, V. Case Studies of Factors Influencing Frequency Response Analysis Measurements and Power Transformer Diagnostics. IEEE Electr. Insul. Mag. 2011, 27, 22–30. [Google Scholar] [CrossRef]
- Tenbohlen, S.; Tahir, M.; Rahimpour, E.; Poulin, B.; Miyazaki, S. A New Approach for High Frequency Modelling of Disc Windings; Cigre Paris: Paris, France, 2018; pp. A2–A214. [Google Scholar]
- Tahir, M.; Tenbohlen, S.; Miyazaki, S. Optimization of FRA by an Improved Numerical Winding Model: Disk Space Variation; VDE-Hochspannungstechnik: Berlin, Germany, 2018. [Google Scholar]
- IEEE Guide for Failure Investigation, Documentation, Analysis, and Reporting for Power Transformers and Shunt Reactors; IEEE std. C57.125-2015; IEEE Standard Association: New York, NY, USA, 2015.
- Mechanical Condition Assessment of Transformer Windings using Frequency Response Analysis (FRA); CIGRÉ WG A2.26; Technical Brochure 342; CIGRE: Paris, France, 2008; ISBN 978-2-85873-030-8.




























© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tahir, M.; Tenbohlen, S. A Comprehensive Analysis of Windings Electrical and Mechanical Faults Using a High-Frequency Model. Energies 2020, 13, 105. https://doi.org/10.3390/en13010105
Tahir M, Tenbohlen S. A Comprehensive Analysis of Windings Electrical and Mechanical Faults Using a High-Frequency Model. Energies. 2020; 13(1):105. https://doi.org/10.3390/en13010105
Chicago/Turabian StyleTahir, Mehran, and Stefan Tenbohlen. 2020. "A Comprehensive Analysis of Windings Electrical and Mechanical Faults Using a High-Frequency Model" Energies 13, no. 1: 105. https://doi.org/10.3390/en13010105
APA StyleTahir, M., & Tenbohlen, S. (2020). A Comprehensive Analysis of Windings Electrical and Mechanical Faults Using a High-Frequency Model. Energies, 13(1), 105. https://doi.org/10.3390/en13010105