Fast Terminal Sliding Mode Control of Permanent Magnet In-Wheel Motor Based on a Fuzzy Controller
Abstract
:1. Introduction
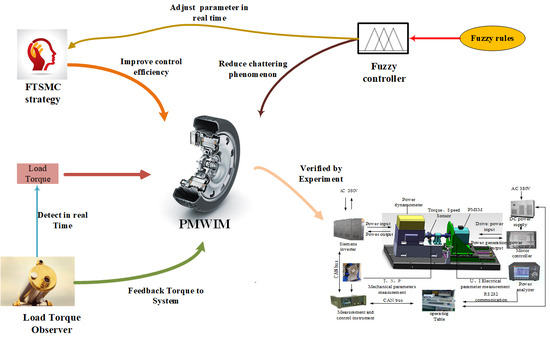
- A novel FTSMC strategy is proposed to realize the rapidity and enhance the robustness of the control system.
- A torque disturbance observer is designed to compensate for the external torque, which improves the control accuracy of the system.
- Fuzzy rules are presented to overcome the chattering phenomenon of the FTSMC, which improves the dynamic performance of the system.
2. Mathematical Model of PMIWMs Fed by a Three-Phase Voltage Source Inverter (VSI)
2.1. Mathematical Model of PMIWMs
2.2. PMIWM Control System Fed by Three-Phase VSI
3. Novel Fuzzy FTSMC Strategy Based on a Load Torque Observer for the PMIWM System
3.1. FTSMC Algorithm for Controlling the System
3.2. Design of the Load Torque Observer
3.3. Design of the Fuzzy Controller
- , then should increase
- , then should decrease
- , then should decrease
- , then should decrease
4. Simulation and Experimentation
- had a better start response performance
- had a smaller overshot phenomenon
- had ideal steady-state performance
- when increasing and decreasing the load, saved about 68% of the adjust time which was needed in the SMC strategy.
- had ideal robust performance
- had a smaller chattering phenomenon because of the design of fuzzy rules.
5. Conclusions
- by implementing the FTSMC approaching law, the main finding is that the proposed method can accelerate the approaching speed of the control system effectively, which can increase the start-up speed and response performance of PMIWMs;
- through torque disturbance observer, the PMIWM control can detect the torque load and compensate it in real time, which effectively decreases the control error and improves the control accuracy;
- the fuzzy controller proposed in this paper can reduce the chattering phenomenon significantly, which can improve the control stability and robust performance of the PMWIM.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Martinez, C.M.; Hu, X.; Cao, D.; Wellers, M. Energy Management in Plug-in Hybrid Electric Vehicles: Recent Progress and a Connected Vehicles Perspective. IEEE Trans. Veh. Technol. 2017, 66, 4534–4549. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Martinez, C.M.; Yang, Y. Charging, power management, and battery degradation mitigation in plug-in hybrid electric vehicles: A unified cost-optimal approach. Mech. Syst. Signal Process. 2017, 87, 4–16. [Google Scholar] [CrossRef]
- Jain, M.; Williamson, S.S. Suitability analysis of in-wheel motor direct drives for electric and hybrid electric vehicles. In Proceedings of the Electrical Power & Energy Conference, Halifax, NS, Canada, 25–27 August 2010. [Google Scholar]
- Shokri, M.; Kebriaei, H. Mean Field Optimal Energy Management of Plug-In Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2018, 68, 113–120. [Google Scholar] [CrossRef]
- Donato, G.D.; Scelba, G.; Pulvirenti, M.; Scarcella, G.; Capponi, F.G. Low-Cost, High-Resolution, Fault-Robust Position and Speed Estimation for PMSM Drives Operating in Safety-Critical Systems. IEEE Trans. Power Electron. 2018, 34, 550–564. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Chen, G. Predictive DTC Strategy with Fault-Tolerant Function for Six-Phase and Three-Phase PMSM Series-Connected Drive System. IEEE Trans. Ind. Electron. 2018, 65, 9101–9112. [Google Scholar] [CrossRef]
- Yong, L.; Li, B.; Xing, X.; Sun, X. A Nonlinear Decoupling Control Approach Using RBFNNI-Based Robust Pole Placement for a Permanent Magnet In-Wheel Motor. IEEE Access 2017, 6, 1844–1854. [Google Scholar]
- Zhou, K.; Sun, Y.C.; Wang, X.D.; Yan, D. Active disturbance rejection control of PMSM speed control system. Electr. Mach. Control 2018, 22, 57–63. [Google Scholar]
- Qin, Y.; He, C.; Shao, X.; Du, H.; Xiang, C.; Dong, M. Vibration mitigation for in-wheel switched reluctance motor driven electric vehicle with dynamic vibration absorbing structures. J. Sound Vib. 2018, 419, 249–267. [Google Scholar] [CrossRef]
- Ouhab, M.; Khatir, Z.; Ibrahim, A.; Ousten, J.; Mitova, R.; Wang, M. New Analytical Model for Real-Time Junction Temperature Estimation of Multi-Chip Power Module Used in a Motor Drive. IEEE Trans. Power Electron. 2018, 33, 5292–5301. [Google Scholar] [CrossRef]
- Li, X.; Sun, Y.; Shen, T. Vibration stability analysis of dual motor harmonic synchronous excitation nonlinear vibration conveyer. Trans. Can. Soc. Mech. Eng. 2018, 42, 419–426. [Google Scholar] [CrossRef]
- Xu, G.; Liu, G.; Shan, J.; Chen, Q. Analysis of a Hybrid Rotor Permanent Magnet Motor Based on Equivalent Magnetic Network. IEEE Trans. Magn. 2018, 54, 8202109. [Google Scholar] [CrossRef]
- Lei, Y.; Ke, W.; Lu, Z.; Ge, Q.; Li, Z.; Li, Y. An Improved Torque and Current Pulsation Suppression Method for Railway Traction Drives Under Fluctuating DC-link Voltage. IEEE Trans. Power Electron. 2017, 33, 8565–8577. [Google Scholar] [CrossRef]
- Yan, R.; Li, B.; Fu, Z. Sensorless control of PMSMs based on parameter-optimized MRAS speed observer. In Proceedings of the IEEE International Conference on Automation & Logistics, Qingdao, China, 1–3 September 2008. [Google Scholar]
- Calligaro, S.; Petrella, R. Accuracy and robustness improvement in sensorless PMSM drives at low-speed by direct-axis current injection. In Proceedings of the IEEE International Conference on Sensorless Control for Electrical Drives, Munich, Germany, 17–19 October 2013. [Google Scholar]
- Jeon, H.; Lee, J.; Han, S.; Kim, J.H.; Hyeon, C.J.; Kim, H.M.; Kang, H.; Ko, T.K.; Yoon, Y.S. PID control of an Electromagnet-based Rotary HTS Flux Pump for maintaining constant field in HTS Synchronous Motors. IEEE Trans. Appl. Supercond. 2018, 28, 5207605. [Google Scholar] [CrossRef]
- Jung, J.W.; Leu, V.Q.; Do, T.D.; Kim, E.; Choi, H.H. Adaptive PID Speed Control Design for Permanent Magnet Synchronous Motor Drives. IEEE Trans. Power Electron. 2014, 30, 900–908. [Google Scholar] [CrossRef]
- Cai, B.; Zhao, Y.; Liu, H.; Xie, M. A Data-Driven Fault Diagnosis Methodology in Three-Phase Inverters for PMSM Drive Systems. IEEE Trans. Power Electron. 2017, 32, 5590–5600. [Google Scholar] [CrossRef]
- Dinardo, L.; Brown, V.; Perez, E.; Bunin, N.; Sullivan, K.E. A single-center study of hematopoietic stem cell transplantation for primary immune deficiencies (PIDD). Pediatr. Transplant. 2012, 16, 63–72. [Google Scholar] [CrossRef]
- Zheng, W.; Wang, X.; Cao, J.; Cheng, M.; Hu, Y. Direct Torque Control of T-NPC Inverters Fed Double-Stator-Winding PMSM Drives With SVM. IEEE Trans. Power Electron. 2018, 33, 1541–1553. [Google Scholar]
- Lin, S.; Zhang, W. An adaptive sliding-mode observer with a tangent function-based PLL structure for position sensorless PMSM drives. Int. J. Electr. Power Energy Syst. 2017, 88, 63–74. [Google Scholar] [CrossRef]
- Qi, Y.; Bostanci, E.; Gurusamy, V.; Akin, B. A Comprehensive Analysis of Short Circuit Current Behavior in PMSM Inter Turn Short Circuit Faults. IEEE Trans. Power Electron. 2018, 33, 10784–10793. [Google Scholar] [CrossRef]
- Aljehaimi, A.M.; Pillay, P. Novel Flux Linkage Estimation Algorithm for a Variable Flux PMSM. IEEE Trans. Ind. Appl. 2018, 54, 2319–2335. [Google Scholar] [CrossRef]
- Liu, B.; Badcock, R.; Hang, S.; Fang, J. A Superconducting Induction Motor with a High Temperature Superconducting Armature: Electromagnetic Theory, Design and Analysis. Energies 2018, 11, 792. [Google Scholar] [CrossRef] [Green Version]
- Malvezzi, F.; Coelho TA, H. Error analysis for an active geometry control suspension system. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 558. [Google Scholar] [CrossRef]
- Schoonhoven, G.; Uddin, M.N. Harmonic Injection-Based Adaptive Control of IPMSM Motor Drive for Reduced Motor Current THD. IEEE Trans. Ind. Appl. 2017, 53, 483–491. [Google Scholar] [CrossRef]
- Jon, U.; Kim, J.; Lee, H. DC Motor Current Control Algorithm Using Proportional-Integral LQT with Disturbance Observer. Int. J. Automot. Technol. 2018, 19, 959–967. [Google Scholar] [CrossRef]
- Wu, Z.; Du, C. The Parameter Identification of PMSM Based on Improved Cuckoo Algorithm. Neural Process. Lett. 2019, 50, 2701–2715. [Google Scholar] [CrossRef]
- Dursun, M.; Boz, A.F.; Kale, M.; Karabacak, M. Sensorless control application of PMSM with a novel adaptation mechanism. Neural Comput. Appl. 2018, 29, 87–103. [Google Scholar] [CrossRef]
- Lukichev, D.V.; Demidova, G.L. Speed control in PMSM drive with non-stiff load and unknown parameters using PI- and fuzzy adaptive PID controllers. In Proceedings of the International Conference on Industrial Engineering, Rome, Italy, 3–5 January 2017. [Google Scholar]
- Chaoui, H.; Khayamy, M.; Aljarboua, A.A. Adaptive Interval Type-2 Fuzzy Logic Control for PMSM Drives with a Modified Reference Frame. IEEE Trans. Ind. Electron. 2017, 64, 3786–3797. [Google Scholar] [CrossRef]
- Saihi, L.; Bouhenna, A.; Chenafa, M.; Mansouri, A. A robust sensorless SMC of PMSM based on sliding mode observer and extended Kalman filter. In Proceedings of the International Conference on Electrical Engineering, Boumerdes, Algeria, 13–15 December 2015. [Google Scholar]
- Huang, H.; Bhuiyan, A.M.Z.; Tu, Q.; Jiang, C.; Xue, J.; Ming, P.; Li, P. Fuzzy sliding mode control of servo control system based on variable speeding approach rate. Soft Comput. 2019, 23, 13477. [Google Scholar] [CrossRef]
- Zhu, J.G.; Lei, G.; Guo, Y.G.; Wang, T.S.; Ma, B. A robust design optimization method for manufacturing SMC-PMSMs and drive systems of six sigma quality. In Proceedings of the 2017 7th International Conference on Power Electronics Systems and Applications—Smart Mobility, Power Transfer & Security (PESA), Hong Kong, China, 12–14 December 2018. [Google Scholar]
- Liu, Z.; Wei, H.; Liu, K.; Zhong, Q.-C. Global Identification of Electrical and Mechanical Parameters in PMSM Drive based on Dynamic Self-Learning PSO. IEEE Trans. Power Electron. 2018, 33, 10858–10871. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, B.; Mao, D. Robust Sliding Mode Control of PMSM Based on a Rapid Nonlinear Tracking Differentiator and Disturbance Observer. Sensors 2018, 18, 1031. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.; Liang, Z.; Zhang, W.; He, X. Research on the Integration of Hybrid Energy Storage System and Dual Three-Phase PMSM Drive in EV. IEEE Trans. Ind. Electron. 2017, 65, 6602–6611. [Google Scholar] [CrossRef]
- Jiang, Y.; Wei, X.; Mu, C.; Liu, Y. Improved Deadbeat Predictive Current Control Combined Sliding Mode Strategy for PMSM Drive System. IEEE Trans. Veh. Technol. 2017, 67, 251–263. [Google Scholar] [CrossRef]
- Mendoza-Mondragón, F.; Hernández-Guzmán, V.M.; Rodríguez-Reséndiz, J. Robust Speed Control of Permanent Magnet Synchronous Motors Using Two-Degrees-of-Freedom Control. IEEE Trans. Ind. Electron. 2018, 65, 6099–6108. [Google Scholar] [CrossRef]
- Yan, J.; Wang, H.; Huang, S.; Lan, Y. Load Disturbance Observer-Based Complementary Sliding Mode Control for PMSM of the Mine Traction Electric Locomotive. Int. J. Fuzzy Syst. 2019, 21, 1051–1058. [Google Scholar] [CrossRef]
- Hao, Y.; Xu, Y.; Cai, F.; Zhang, H.; Zhao, W.; Gerada, C. PWM-VSI Fault Diagnosis for PMSM Drive Based on Fuzzy Logic Approach. IEEE Trans. Power Electron. 2018, 34, 759–768. [Google Scholar]
- Choi, G.; Jahns, T.M. Analysis and Design Recommendations to Mitigate Demagnetization Vulnerability in Surface PM Synchronous Machines. IEEE Trans. Ind. Appl. 2018, 99, 1. [Google Scholar] [CrossRef]
- Guzinski, J.; Abu-Rub, H.; Diguet, M.; Krzeminski, Z.; Lewicki, A. Speed and Load Torque Observer Application in High-Speed Train Electric Drive. IEEE Trans. Ind. Electron. 2010, 57, 565–574. [Google Scholar] [CrossRef]















| K(t) | |||||||
|---|---|---|---|---|---|---|---|
| s | |||||||
| NM | PM | ||||||
| PM | |||||||
| Symbol | Quantity | Value |
|---|---|---|
| B | Viscous friction coefficient | 0.006 Nms |
| Lq | Inductance of q axis | 8.0 mH |
| Ld | Inductance of d axis | 8.0 mH |
| J | Moment of inertia | 0.002 kgm2 |
| ψ | Rotor’s magnetic flux | 0.185 Wb |
| R | Nominal phase resistance | 2.315 Ω |
| P | Number of pole pairs | 4 |
| f | Switching frequency | 8 kHz |
| Q | Rated power | 5 kw |
| Change Parameters | SMC Strategy | FTSMC Strategy |
|---|---|---|
| Startup time (s) | 0.207 | 0.055 |
| Fluctuation | 2.5% | 1.2% |
| Adjust time (15 N·m) (s) | 0.113 | 0.037 |
| Adjust time (−15 N·m) (s) | 0.121 | 0.034 |
| Overshoot | 5.76% | 3.7% |
| Change Parameters | SMC Strategy | FSMC Strategy | FTSMC Strategy |
|---|---|---|---|
| Approaching time (x1) (s) | 2.832 | 2.125 | 1.121 |
| Approaching time (x2) (s) | 2.821 | 1.986 | 1.861 |
| Approaching time (U) (s) | 2.829 | 2.045 | 1.831 |
| Fluctuation (U) | 2.112 | 2.102 | 1.980 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Tu, Q.; Pan, M.; Jiang, C.; Xue, J. Fast Terminal Sliding Mode Control of Permanent Magnet In-Wheel Motor Based on a Fuzzy Controller. Energies 2020, 13, 188. https://doi.org/10.3390/en13010188
Huang H, Tu Q, Pan M, Jiang C, Xue J. Fast Terminal Sliding Mode Control of Permanent Magnet In-Wheel Motor Based on a Fuzzy Controller. Energies. 2020; 13(1):188. https://doi.org/10.3390/en13010188
Chicago/Turabian StyleHuang, Hao, Qunzhang Tu, Ming Pan, Chenming Jiang, and Jinhong Xue. 2020. "Fast Terminal Sliding Mode Control of Permanent Magnet In-Wheel Motor Based on a Fuzzy Controller" Energies 13, no. 1: 188. https://doi.org/10.3390/en13010188
APA StyleHuang, H., Tu, Q., Pan, M., Jiang, C., & Xue, J. (2020). Fast Terminal Sliding Mode Control of Permanent Magnet In-Wheel Motor Based on a Fuzzy Controller. Energies, 13(1), 188. https://doi.org/10.3390/en13010188