Control of Heat Pumps with CO₂ Emission Intensity Forecasts

Abstract

An optimized heat pump control for building heating was developed for minimizing CO${}_2$ emissions from related electrical power generation. The control is using weather and CO${}_2$ emission forecasts as inputs to a Model Predictive Control (MPC)—a multivariate control algorithm using a dynamic process model, constraints and a cost function to be minimized. In a simulation study, the control was applied using weather and power grid conditions during a full-year period in 2017–2018 for the power bidding zone DK2 (East, Denmark). Two scenarios were studied; one with a family house and one with an office building. The buildings were dimensioned based on standards and building codes/regulations. The main results are measured as the CO${}_2$ emission savings relative to a classical thermostatic control. Note that this only measures the gain achieved using the MPC control, that is, the energy flexibility, not the absolute savings. The results show that around 16% of savings could have been achieved during the period in well-insulated new buildings with floor heating. Further, a sensitivity analysis was carried out to evaluate the effect of various building properties, for example, level of insulation and thermal capacity. Danish building codes from 1977 and forward were used as benchmarks for insulation levels. It was shown that both insulation and thermal mass influence the achievable flexibility savings, especially for floor heating. Buildings that comply with building codes later than 1979 could provide flexibility emission savings of around 10%, while buildings that comply with earlier codes provided savings in the range of 0–5% depending on the heating system and thermal mass.

1. Introduction

Energy flexibility on the electricity market is a high focus area in modern energy policies scoping in on storage (e.g., batteries, fuel cells, hydro reservoirs, thermal) and flexible demand (e.g., heat pumps, electric cars) [1]. The aim is to decrease CO${}_2$ emissions by meeting the fluctuating proportion of renewable sources (e.g., solar, wind) vs nonrenewable sources (e.g., coal, gas, nuclear). Ideally, in the future, electricity users (the demand) will respond to the renewable power generation levels in an attempt to minimize emissions—in a 100% renewable scenario storage and flexibility is a must for operating the power system [2].

Therefore, methods for identifying the flexibility potential in various applications are developed. In Reference [3], the energy flexibility potential in buildings is identified by the so-called Flexibility Index, which is the energy cost, from a penalty-aware control, relative to a penalty-ignorant control. The penalty could be for example, a CO${}_2$ or price signal. The present paper investigates the energy flexibility potential in buildings with a focus on heat pumps.

Heat pumps have different sizes and applications, from small single building heat pumps to large heat pumps for district heating. The scope of the present study is limited to investigate the increasing potential in single building heat pumps—which has been almost four-fold from 2011 to 2019 while the number of oil-fired boilers have decreased by roughly one third in the same period [4]. Many oil-fired boilers are replaced with heat pumps—due to both economic and environmental benefits and political pressure (bans of oil-fired boilers in certain districts for new buildings [5].) The control of the heating, however, are often simple thermostatic controls. This often results in heating when electricity demand is high (e.g., afternoon and evening peaks), leading to increased system stress, resulting in increased fossil fuel consumption. It is, therefore, an opportunity to shift the demand away from peak hours using the heat-storing potential of the buildings.

In a power system, the generator which is responding to small changes in demand (e.g., start-up of a heat pump) is called the marginal generator. A reasonable estimate of the marginal generator is achieved by using price signals, see Figure 1—the merit order illustrated with a supply/demand curve; the x-axis has the accumulated supply generators and the y-axis is the corresponding price. A small increase in demand (dashed blue line) illustrates the marginal generator—in this case, a coal fired Combined Heat and Power (CHP) plant.

Due to both grid stability, economic and environmental benefits, day-ahead spot price-based control strategies have been proposed in recent papers [6,7,8], using occupancy mode detection and rule-based price control and Model Predictive Control (MPC) (a multivariate predictive control algorithm using a dynamic process model, constraints and a cost function to be minimized). In Reference [6], MPC is used with varying electricity prices to minimize the cost of operating a heat pump connected to a storage unit and a floor heating system. The control only heats at night, where the prices are low, and it is assumed that the heat pump and storage are large enough to accumulate enough heat for the whole day. Cost savings of between 25% to 30% are obtained. MPC is a well-known concept in building automation control literature [9,10,11,12,13], and proven to be promising with respect to minimizing costs, but a broad practical implementation still has various challenges discussed in Reference [14].

In Reference [10], the importance of occupancy information is highlighted and evaluated on a daily basis. However, a higher resolution is needed to incorporate variations throughout the day (e.g., when people are at work). In the study in Reference [7] occupancy modes are used together with price signals to control a heat pump. The occupancy modes were developed in The Olympic Peninsula project [15] and describe work, night and home mode, each with a corresponding set point and price sensitivity. The study showed a significant level of load shifting, leveling out the normal peaks in the daily demand curve. A self-learning controller was applied and adapts easily to changing consumer habits.

There is a problem with spot prices though, known as the merit order emission dilemma, as illustrated in Reference [16] for the German-Austrian power market: The price for coal is low but the emissions are high. A price-based control, therefore, only leads to a decrease in emissions if there is a surplus of renewable energy (more renewable energy than needed)—otherwise coal is favored, and it is therefore encouraged to use CO${}_2$ emission signals instead.

For CO${}_2$ emissions, two distinct measures are used: average and marginal emission intensities, both with the units $\left(\frac{{\mathrm{kgCO}}_2-\mathrm{eq}}{\mathrm{MWh}}\right)$. Average emissions correspond to the overall, for example, region-wide, electricity production including net imports. The marginal reflects the emissions of the marginal generator. The concepts are compared in Reference [17] and the importance of distinguishing between the two is highlighted due to their very opposing patterns. It is emphasized that the marginal emission is the most optimal signal to use for control.

In Reference [8], the average CO${}_2$ emission intensity and price signals are used in heat pump control of residential buildings in Norway (known for low emissions due to large amount of hydropower) with Predictive Rule-Based Control (uses predefined thresholds to give information about when the emissions are low). it is concluded that with price-based control, the overall CO${}_2$ emissions have actually increased (evaluated using the average emissions). It is argued to result from the load being shifted to the night time, where cheap carbon-intensive electricity is imported from the continental European power grid. This is either a great example of the merit order dilemma or a result that may have been different if marginal emissions had been used.

A recent study [18] investigated marginal emissions and uses estimates provided by Tomorrow (www.tmrow.com) to develop a 24-h forecast using a machine learning approach on historical data. The CO${}_2$ estimates are calculated with the empirical method developed in Reference [19] using historical data from European bidding zones. The chain of imports (the so-called flow tracing, originally introduced in Reference [20,21]) is followed to assess the impact of a specific generator or load on the power system. This is a large scale solution using data from the majority of bidding zones around the world.

In the present study, MPC is used for control for heating a building. This allows using knowledge of future indoor climate states, CO${}_2$ emissions and weather conditions to schedule heat pump operation. It is a linear approach, which has its limits and requires simplifications, investigated and discussed in Reference [22]. The simplifications include neglecting the effect on the efficiency from factors, for example, frequency variations in the compressor (a main component in a heat pump) and temperature variations. The paper concludes that neglecting these factors can lead to significant errors. The frequency variations are, however, are not used in this study. From Reference [22], the frequency is noticed to be the least important factor and is specifically justified when using varying electricity prices, because the heat pump mostly operates at nominal speed to maximize the heat output when prices are low. The impact from the outdoor temperature is accounted for—this is important because it means the efficiency is lower during the night, where also the emissions are low.

In order to model the heat dynamics in the building, a lumped dynamic process model is applied [23]. A tricky part is to determine the values of the parameters appropriately, for example, insulation level and heat capacity: if the right type of measured data is available, the parameters can be estimated [24], or they can be calculated according to physics. In the present study physics are used and a sensitivity analysis is carried out to map the impact of parameters on the CO${}_2$ savings potential. Such a sensitivity analysis is lacking in the literature. In some papers transparency is lost, since the impact of the parameters is not elucidated, thus increasing the risk of biased results. This paper addresses both of these issues by using historic danish building codes from 1977 and later to describe the insulation thickness as a parameter along with the heat pump size and thermal capacity of floor in two hypothetical buildings: a family house and an office building. Further, the impact of using forecasts is assessed by comparing the savings achieved with known future weather (perfect forecasts) vs. real forecasts.

It is noted that the emission saving potential using an MPC, that is, flexible demand, is measured as CO${}_2$ emission savings relative to classical thermostatic control, that is, non-flexible demand. Hence, the results express only the potential of energy flexibility, not the absolute emission savings.

In Section 2, the weather data and marginal CO${}_2$ emissions are presented. The dynamic process model is presented in Section 3 as an RC-diagram together with the MPC which is written up as a linear programming formulation. The efficiency of the heat pump is modelled as a temperature-dependent variable but neglects the compressor frequency. In Section 4 the building codes, temperature settings and model parameters are discussed. The results are presented in Section 5 as graphs showing the CO${}_2$ emission reductions vs selected parameters—for example, heat pump size, concrete and building regulation year.

2. Data

Data provided by Tomorrow (www.tmrow.com) is used in the study. It comprises the marginal CO${}_2$ emission data and weather forecasts (temperature and solar irradiation) to model the building thermodynamics and heat pump planning—see Figure 2. The emissions show close to none seasonality except the winter, where the intensity peaks. Both the temperature and solar radiation are highly seasonal with a hot climate and high solar radiation in the summer—reversed in the winter.

Only the CO${}_2$ emissions are provided in both real-time values and forecasts. The real-time weather conditions are, however, also essential for the model to describe the actual building thermodynamics. The solar irradiation forecast is plotted in Figure 3 (left plot) for the 21st of June. Every sixth hour a new forecast is provided, at 2 a.m., 8 a.m., 2 p.m. and 8 p.m. The gaps between the forecasts are significant and illustrate the inaccuracy of the prediction for long horizons.

For modelling purposes, the real-time weather conditions are modelled from the forecasts. Assuming horizons for $h=1$ are the most accurate forecasts, a kernel smoothing process using splines and a weight for short horizon favouritism is applied—see Appendix A for a description of the approach. The result for solar radiation is the smoothing curve seen in Figure 3, right plot. The temperature forecasts did not show any significant gaps, suggesting all horizons, 1–6, are more correct models of the real-time condition than the solar radiation.

3. Model

The model is a state-space model, derived from thermodynamic state equations describing the heat dynamics in the building as a lumped dynamic process model [25]. The model parameters are defined based on the building composition and structure. However, if the correct measurement data is available the model parameters could be estimated as in Reference [26], thus it would be easy to use the applied control setup in existing buildings, without the need for information about the building composition.

3.1. Assumptions

It is assumed that the building is just one big room with a flat roof. Thereto the following assumptions have been made; one uniform air temperature; no ventilation; no influence from the humidity of the air; no influence from the wind. The heat pump is assumed to be static because its dynamics are much faster than those of the building. Heat pumps require power to move heat from a cold space to a hot space using a refrigerant (it extracts heat from a cold space through an evaporator and delivers that heat to the hot space through a condenser). The heat pump efficiency is described using the COP-factor (Coefficient Of Performance). The maximum efficiency is modelled as the Carnot Efficiency [27] by

$$\begin{array}{c}\hfill {\mathrm{COP}}_{\mathrm{Carnot}}={\left(1-\frac{T_{\mathrm{cold}}}{T_{\mathrm{hot}}}\right)}^{-1},\end{array}$$

(1)

where $T_{\mathrm{hot}}$ represents the condensation temperature, which is the temperature of the water flowing in the heating system (fluctuating in reality, but simplified to a constant = 40 ${}^{\circ }$C). $T_{cold}$ is the ambient evaporation temperature. However, the COP-factor is smaller in reality and therefore it is multiplied by another efficiency $\eta$, which can be assumed to be between 50% and 70% [28]. To be conservative, it has been set to 50% in the calculations. Therefore, the COP factor is expressed as

$$\begin{array}{c}\hfill f_{\mathrm{cop}}(T_{\mathrm{hot}},T_{\mathrm{cold}})=\eta ·{\mathrm{COP}}_{\mathrm{Carnot}}.\end{array}$$

(2)

3.2. State Space Equations

The state-space model is defined by dividing the building into three sections; ‘Floor’, ‘Interior’, and ‘Inner envelope’. Inner refers to the part of the walls and roof that is on the inside of the insulation.

The goal is to determine the temperature dynamics in the three sections. Thermodynamics can very well be explained in the same way as electric circuits, which will provide a nice analytic approach. The model is shown as the commonly used RC-diagram [24], in Figure 4.

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{T}_t^f}{\mathrm{dt}}& =\frac{1}{C_{\mathrm{f}}}\left(\frac{T_t^i-T_t^f}{R_{\mathrm{f},\mathrm{i}}}+(1-{\mathsf{\Psi }}_s)g_{\mathrm{A}}{\mathsf{\Phi }}_t^s+(1-{\mathsf{\Psi }}_h){\mathsf{\Phi }}_t^h\right)\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{T}_t^i}{\mathrm{dt}}& =\frac{1}{C_{\mathrm{i}}}\left(\frac{T_t^f-T_t^i}{R_{\mathrm{f},\mathrm{i}}}+\frac{T_t^w-T_t^i}{R_{\mathrm{i},\mathrm{e}}}+{\mathsf{\Psi }}_s{g}_{\mathrm{A}}{\mathsf{\Phi }}_t^s+{\mathsf{\Phi }}_t^h{\mathsf{\Psi }}_h\right)\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{T}_t^w}{\mathrm{dt}}& =\frac{1}{C_{\mathrm{e}}}\left(\frac{T_t^i-T_t^w}{R_{\mathrm{i},\mathrm{e}}}+\frac{T_a-T_t^w}{R_{\mathrm{e},\mathrm{a}}}\right)\hfill \end{array}$$

(5)

Refer to the nomenclature in Section 1 for variable definitions. ${\mathsf{\Psi }}_h$ is a logic variable integer (0,1) defining the heat system ($\mathsf{\Psi }=1$ for radiators and $\mathsf{\Psi }=0$ for floor heating). The heat delivered to the respective zones from the heat pump is

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_t^h=f_{\mathrm{cop}}(40,T_t^a)·P_t^e,\end{array}$$

(6)

where $P_t^e$ is the electrical power used by the heat pump. The solar irradiation $P_t^s$ is going through the windows and heating both the floor and the room. ${\mathsf{\Psi }}_s$ describes the fraction that heats the room.

3.3. MPC

The model is transformed from continuous into discrete-time, see Reference [24]. The discrete-time linear state space model is written as

$$\begin{array}{cc}\hfill {\mathit{x}}_t& =\mathit{A}{\mathit{x}}_{t-1}+\mathit{B}{u}_{t-1}+\mathit{E}{\mathbf{d}}_{t-1}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill y& =\mathit{C}{\mathit{x}}_{t-1}+{ϵ}_{t-1},\hfill \end{array}$$

(8)

where $\mathit{x}$ is the state vector (building temperatures) and u is the controllable input vector describing is the electrical power to the heat pump, since the heat output from the heat pump, ${\mathsf{\Phi }}_{\mathrm{h}}$, is a function of both the power input signal and the COP factor. $\mathbf{d}$ is the disturbances, which in this case is the outdoor temperature and solar irradiation. $y_t$ is thus the controllable variable $T_t^i$ plus some error ${ϵ}_t$. Hence

$${\mathit{x}}_t=\left[\begin{array}{c}{T}_t^i\\ T_t^f\\ T_t^w\end{array}\right]u_t=\left[\begin{array}{c}{P}_t^e\end{array}\right]{\mathit{d}}_t=\left[\begin{array}{c}{T}_t^a\\ G_t\end{array}\right].$$

(9)

The matrix A states the dynamic behavior of the system, whereas matrix B specifies how the controllable input signals enter the system, and E specifies the uncontrollable input signals. Furthermore, $\mathit{C}$ is a constant matrix that specifies the controllable state(s), in this case, $\mathit{C}=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]$. For a deeper explanation, please refer to References [6,24].

The MPC then becomes a linear programming problem formulated as

$$\begin{array}{cc}\underset{u_s,v_k}{\arg \min }\hfill & {\displaystyle \sum _{k=1}^N{\lambda }_{t+k}{u}_{t+k}+p_k{v}_{t+k}}\hfill \\ \mathrm{subject}\mathrm{to}\hfill & {\mathit{X}}_{s+1}=\mathit{A}{\mathit{X}}_s+\mathit{B}{\mathit{u}}_s+\mathit{E}{\mathit{D}}_s\hfill \\ \hfill & T_{\min }\le \mathit{C}{\mathit{X}}_{s+1}+v_{s+1}\hfill \\ \hfill & T_{\max }\ge \mathit{C}{\mathit{X}}_{s+1}-v_{s+1}\hfill \\ \hfill & 0\le u_s\le P_{\max }\hfill \\ \hfill & v_s\ge 0\hfill \\ \hfill & \forall s\in \{t,t+1,t+2,...,t+N\}\hfill \end{array},$$

(10)

where ${\lambda }_{t+k}$ is the penalty at time $t+k$, which in this case is the marginal CO${}_2$ emission intensity. N is the prediction horizon. At each sampling time, the linear program is solved to obtain the heating schedule $[u_{t+1},u_{t+2},...,u_{t+N}]$. P_max is the maximum power input signal the heat pump can receive. As it may not always be possible to meet the temperature demand, a slack variable $v_k$ is introduced and connected to the violation penalty $p_v$. This value is set relatively high to avoid temperature violations.

This linear program is solved using lpsolve interfaced with the R-package lpSolve, [29].

4. Inputs for the Model

In this section, the reference buildings and input data are presented.

The Danish building codes specify the building law requirements and contain detailed requirements for all construction work. This study evaluates the building codes from 1977 to 2018, denoted BC_year. The minimum requirements for outer walls, roof, windows and doors are listed by year in

Table 1. Building code requirements to insulation properties by year. Windows requirements are speficied with both U-values, glazing (g) and the estimated net heat transfer through the window into the room, $E_{\mathrm{ref}}$ (follows; $E_{\mathrm{ref}}=194.4$ g$-90.36$ U ).

BC	Walls	Roof	Doors	Windows
Year	$\mathit{U}\left[\frac{\mathbf{W}}{{\mathbf{m}}^2\mathbf{K}}\right]$	$\mathit{U}\left[\frac{\mathbf{W}}{{\mathbf{m}}^2\mathbf{K}}\right]$	$\mathit{U}\left[\frac{\mathbf{W}}{{\mathbf{m}}^2\mathbf{K}}\right]$	$\mathit{U}\left[\frac{\mathbf{W}}{{\mathbf{m}}^2\mathbf{K}}\right]$	${\mathit{E}}_{\mathit{r}\mathit{e}\mathit{f}}\left[\frac{\mathbf{kWh}}{{\mathbf{m}}^2}\right]$	$\mathit{g}[-]$
1977	1	0.45	3.6	3.6	−174.314 **	0.777 **
1979–1985	0.4	0.2	2	2.9	−117.378 **	0.744 **
1995–1998	0.4	0.2	2	2.3	−69.934 **	0.709 **
2008	0.4	0.2	2	2	−46.909 **	0.688 **
2010	0.3	0.2	2	1.8 **	−33	0.673 **
2015–2018	0.14 *	0.1 *	2	1.6 **	−17	0.654 **

* U-values from ROCKWOOL A/S [30] needed to comply with the building envelope requirements. For the considered buildings the given U-values in BC${}_{1977:2010}$ are strict enough to comply with the respective envelope requirements.

** Estimated values: From 2010, the windows insulation properties are described by $E_{\mathrm{ref}}$. An exponential relationship between U and the glazing (g) is found from key numbers of different window types to be; $U=0.0205e^{6.6545g}$ [31]. This essentially allows U and g to be calculated from $E_{\mathrm{ref}}$.

.

Two different types of buildings are considered; a family house and an office building, they differ in size and minimum temperature time settings during a nightly setback. The night time setpoint is 18 ${}^{\circ }$C for (11 p.m.:5 a.m.) and (6 p.m.:7 a.m.) respectively for the family house and office building. During the day, the set point is 20 ${}^{\circ }$C. The specific model parameters for each building are listed in

Table 2. Building dimensions and model parameters for both buildings based on BC${}_{2018}$—calculations are  as specified in Appendix C.

		Family House	Office Building
$A_f$	${\mathrm{m}}^2$	156	1250
$A_w$	${\mathrm{m}}^2$	107	302
$A_{\mathrm{doors}}$	${\mathrm{m}}^2$	4	13
$A_{\mathrm{windows}}$	${\mathrm{m}}^2$	14	39
$R_{\mathrm{e},\mathrm{a}}$	$\frac{\mathrm{K}}{\mathrm{kW}}$	10.398	2.379
$R_{\mathrm{i},\mathrm{e}}$	$\frac{\mathrm{K}}{\mathrm{kW}}$	1.190	0.269
$R_{\mathrm{f},\mathrm{i}}$	$\frac{\mathrm{K}}{\mathrm{kW}}$	1.442	0.180
$C_{\mathrm{e}}$	$\frac{\mathrm{kWh}}{\mathrm{K}}$	7.508	39.527
$C_{\mathrm{f}}$	$\frac{\mathrm{kWh}}{\mathrm{K}}$	3.198	25.623
$C_{\mathrm{i}}$	$\frac{\mathrm{kWh}}{\mathrm{K}}$	0.876	6.944

* The window and door area is determined from a window-to-wall ratio of 0.11 and a door-to-wall ratio of 0.04.

for a default case complying with BC${}_{2015:2018}$.

For the sake of simplicity, the buildings are squares with one story. Typical building part constructions are used, illustrated in Appendix B. The thickness of the concrete layers will be varied in the analysis.

The construction material properties are listed in

Table A1. Thickness ($\zeta$), density ($\rho$), heat capacity ($\mathbf{C}$), thermal conductivity ($\mathit{k}$) and thermal resistance ($\mathit{R}$) of all the building parts. The thermal resistance is; $\mathit{R}=\frac{\zeta }{\mathit{k}}$. Thicknesses are examples for a BR18 building.

in Appendix C, where also the building dimensions and model parameters are defined.

The windows are defined as equal sizes on each side of the house pointing in north, east, south and west respectively with a window-to-wall ratio of 0.11 (the proportion of the wall that is windows). The R-package solaR is used for solar radiation inclination angle calculations. ${\mathsf{\Psi }}_s$ is set to 0.1 as in Reference [6].

Dimensioning of the heat pump is based on the heat loss from the buildings, specified in Appendix C.

Forecasts

24 h horizon CO${}_2$ emission forecasts presented in the related paper, [18], are used. The real-time values are presented in Section 2 along with estimated real-time values of the temperature and solar radiation. The weather forecasts have horizons of 24 h too.

To evaluate the MPC and the impact of using forecasts, different extreme cases are defined:

• Case_Ideal: This takes the exact value of a future CO${}_2$ emission intensity as prediction hence, a perfect forecast. This provides an upper limit of CO${}_2$ savings.
• Case_Real: This takes the CO${}_2$ emission forecast developed in Reference [18] and represents the performance of the MPC with real forecasts.
• Case_Trivial: This makes no use of forecasts and will thus result in a non predictive controller that simply controls the heat pump keeping the temperature at the lower limit if possible.

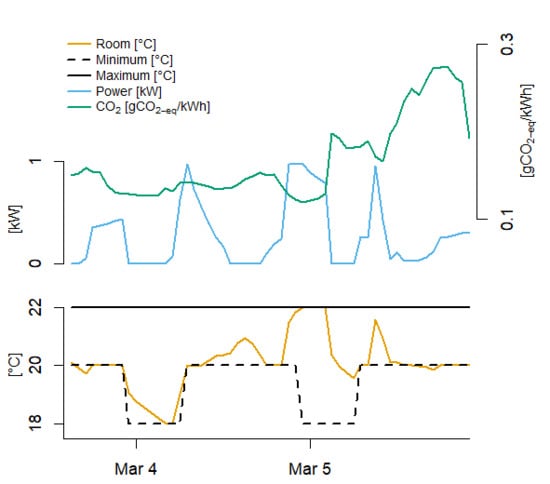
5. Results and Discussion

In this section, various conditions and parameters are evaluated, for example, effect of horizon length, heat pump size, insulation and concrete thicknesses. The radiator and floor heating system is compared throughout the analysis along with the family house versus the office building. The criteria to be optimized is the CO${}_2$ emission savings. The total emissions are calculated from: $\mathsf{\Lambda }\left(\mathrm{Case}\right)={\sum }_{t=1}^{n-N}{u}_{\mathrm{Case},t}{\lambda }_t$, where n is the number of data points presented in Section 2 ($n=8688$) and the ‘Case’ denotes one of the three cases defined in Section 4. The savings are thus calculated as the flexibility index [32] by

$$\mathit{Savings}\left(\mathit{Case}\right)=\frac{\mathsf{\Lambda }\left({\mathrm{Case}}_{\mathrm{Trivial}}\right)-\mathsf{\Lambda }\left(\mathrm{Case}\right)}{\mathsf{\Lambda }\left({\mathrm{Case}}_{\mathrm{Trivial}}\right)}$$

(11)

As previously noted, this measure indicates the relative savings from utilizing the energy flexibility, hence not the absolute savings. If not otherwise stated the results are calculated with a building complying with BC₂₀₁₈, see Table 1.

The parameters that will be investigated are:

• Heating system and varying set points: Both radiator and floor heating are considered and the use of varying set points (lower temperature during the night).
• Horizon of forecasts: To get an idea about how long horizons actually are needed to get a well performing MPC.
• Size of heat pumps: Essential for comparing the buildings and to know whether the potential is reached. Also economically, this is important because as the price increases with larger heat pumps. This will become a compromise between price and CO${}_2$ emission. The default values for the family house and office are the minimum sizes required to meet the heat demand on the coldest day (−12 ${}^{\circ }$C); 3 and 13 kW_heat respectively Appendix (see Appendix C for calculations). Requirements are thus a 1 and 4.3 kW input signal respectively according to Equation (1).
• Insulation and concrete thicknesses: These will be adjusted to see the impact of levels of insulation and heat capacity. The default thicknesses and material properties are shown in Appendix C.

An example of the differences between the cases, and the radiator and floor heating, is illustrated in Figure 5. The resulting electrical power and temperature for Case_Trivial and Case_Real on a four day period for the family house is shown. The result of Case_Trivial is slightly different for the two heating systems. With radiators, it needs to heat more continuously than the floor heating throughout the day. This is because the radiators transfer the heat directly to the internal air, and not through the large heat capacity in the floor, resulting in a much faster response. In both cases, the heating is switched off during the night time to reach the lower set point. However, the floor heating violates the temperature restrictions more during the morning while heating the house, which is due to its slow response. Case_Real seeks to only switch on the heat pump during low emission periods. The radiator system does this well, but it is clearly limited by the maximum indoor temperature limit and the power input decays immediately to avoid temperature violation. In the floor heating system, the heat pump can operate at full load for a longer time using the floor as storage. An interesting point is that using day and night profiles, Case_Real has no benefits of letting the temperature drop during the night because of: (i) the temperature response is too slow and (ii) the emissions are usually lowest during the night, so this is the best time to use the heat pump. Contrarily, the indoor temperature in the radiator system occasionally drops during the night if there is no significant drop in CO${}_2$ emissions.

As expected, throughout almost a year ($n=8688$ h) the floor heating system provides slightly more flexibility and reaches savings of 11% against 9% using radiators for the whole year for Case_Real.

The control horizon needs to be sufficiently long for the MPC to provide flexibility to the system (Figure 6). Note, the savings from floor heating become negative when using low control horizons. The nightly setback causes that; Case_Trivial switches on at six AM every morning and the emission peak is happening already at four AM (Figure 7). For example, when using a two-hour control horizon, the heat pump will be forced to switch on at four AM instead and thus increase the emissions.

Interesting to note is the changing behaviour of the curves around the eight hours horizon: Case${}_{Ideal}$ in the family house with radiators has no savings up until this point. Like any other energy storage, a loss is introduced, in this case, by an increase in temperature resulting in a higher heat loss. Therefore, the MPC will only store heat if the CO${}_2$ variations are large enough for the resulting emissions to break even with the increased losses. These variations become sufficiently large around eight hours. This is less of a problem for the floor heating system, as the loss is much lower. This behaviour is less pronounced in the office building with radiators because the volume to surface area increases with larger buildings, hence the heat capacity increases relative to the surface area.

The loss in savings due to forecast errors, can be found from the difference between Ideal and Real. The radiator system is close to reaching its full potential, where the floor heating still can improve maximum about 5% savings from better forecasts.

Finally, it is noted, that there is still an increase in savings at the 24 h horizon, for all scenarios, indicating that even longer horizons will lead to further increase in savings.

Increasing the heat pump size can lead to slightly higher savings (Figure 8), as more heat can be produced around the small-time slots with low emission. This is especially true when using floor heating, due to the high heat capacity in the floor. For the radiator systems, there is no significant gain for either the family house nor the office building. For the family house with floor heating, there is a relatively large gain when considering Case${}_{Ideal}$, while Case${}_{Real}$ only reaches a slight improvement. There are significantly higher savings to achieve from Case${}_{Real}$ in the office building; because of the larger floor to wall area ratio (more heat capacity relative to the area the heat can escape through), a larger heat pump can accumulate more heat and thereby increase the flexibility.

The impact from insulation is evaluated with respect to the development of building codes from 1977 and forward, which has been an increase in insulation, window and door requirements (see Table 1 for building code specs and corresponding physical values). Another important aspect is the concrete thickness in the floor because it increases the heat capacity and thus the heat storage capabilities. Generally, BC${}_{1977}$ houses have very minimal because of the low insulation restrictions—significantly improved in BC${}_{1979}$ (Figure 9 and

Table 3. Min. savings are derived from a concrete thickness of 10 mm. Max. savings are derived from concrete thicknesses of 200 mm by default.

	Floor		Radiator
	BC${}_{\mathbf{1977}}$	BC${}_{\mathbf{2015}:\mathbf{2018}}$	BC${}_{\mathbf{1977}}$	BC${}_{\mathbf{2015}:\mathbf{2018}}$
Family house
Min. savings	0.5%	9.4%	1.8%	9.9%
Max. savings	2.7%	17.4%	2.8%	12.4%
Office building
Min. savings	1.4%	7.8%	2.4%	8.1%
Max. savings	9.2%	16.0%	4.1%	12.3%

* Optimal concrete thickness of 50 mm. ** Optimal concrete thickness of 80 mm.

). However, the office building using floor heating can provide savings of around 9% with 200 mm of floor concrete and following BC${}_{1977}$ restrictions. This is due to the floor to wall ratio—the larger it is, the more the concrete thickness in the floor can contribute, and the less the insulation in the walls contributes.

For radiator heating, the concrete thickness in the floor is not very important for the savings. Still, adding 50–80 mm can increase the savings by around 2.5–4% (Table 3), but any thicker layer will not increase the savings at all (i.e., the red colored area in the graphs for radiator heating can hardly be seen— Figure 9). The insulation thickness in the office building using radiators seems saturated after BC${}_{1979}$. This may seem counter-intuitive, but in reality, with high thermal resistance, the model becomes more rigid and therefore, less flexibility is allowed to occur. Of course, the absolute CO₂ emission savings will increase with more insulation.

Floor heating in a thick concrete floor provides the most flexibility in both buildings (around 16–17% in both with 200 mm concrete and BC${}_{2015:2018}$). This setup exploits the full potential of the large heat storage in the floor, but lacks to exploit the nightly decrease in set point, because of the slow temperature response. With only 10 mm of concrete, the savings are almost identical for radiator and floor heating (about 6% with BC${}_{2015:2018}$ in all cases). Note that a concrete thickness of 10 mm is not common practise.

This study only measured the relative savings, but the absolute savings will, of course, also increase with more insulation. Therefore, if a house is not well insulated, the first attempt to decrease CO${}_2$ emissions should be to reduce the heat demand by adding insulation before trying to optimize the control. As a result of new regulations in BC${}_{1979}$, buildings in Denmark built before 1979 have been increasingly re-insulated to decrease the heat demand and costs. In Reference [33], it is found that the actual heat demand is on average lower than the theoretical calculations based on registered building data. This could imply that buildings indeed are re-insulated without further registration.

Most buildings in Denmark are built before 1979 [4], and this group is therefore the best representative for the potential buildings—floor heating is rarely the main heating system in this group. It would thus follow the early end of the radiator curves in Figure 9 with re-insulated buildings likely to comply with BC${}_{1979}$. Therefore, between 4% and 7% of savings can be expected. However, new buildings complying with BC${}_{2015–2018}$ envelope requirements and floor heating installed may reach savings of nearly 17%. Often, buildings combine radiators and floor heating and rely not only on one or the other, thus in reality have the advantages from both systems can be utilized depending on the heated rooms. Recall from Figure 5, the radiators are good at quick responses and therefore allows the temperature to decrease during the night contrarily to the floor heating. However, it has little capability of storing heat for more extended periods. The potential for this is open to further studies.

The average daily load for a BC${}_{2015–2018}$ family house has shifted significantly (Figure 7). The trivial control follows to a certain degree the emissions throughout a day. The natural need for heating is therefore very inconvenient for the emissions and illustrates why energy flexibility is important. The MPC smooths the load during the day, decreasing it at otherwise peak hours and shifts most of the load to operate at midnight despite the lower temperature set point. This illustrates the importance of predictive control—if all houses follow the same schedule, there will be a need for much more additional storage capacity.

In general, this study can be relevant to buildings and scenarios with similar characteristic and climate conditions. Especially in the Nordic countries where the heating system comprises a large chunk of the electricity consumption. In warmer climates the study could be converted into air conditioning rather than heating. The wind and solar power production share was 36% in the examined region for the one year period in 2017 and 2018. The results will change depending on the conditions for example, with higher levels of fluctuating renewable generation in the future [34]. In a 100% renewable scenario it is of course not meaningful to use the CO${}_2$ emissions as minimizing objective, however utilizing energy flexibility will be vital [35].

Model Simplification

The results are based on calculations using a simplified building model of a simplified building with only a single room. If more rooms are considered, it would add more heat capacity from walls dividing the rooms. This could increase the savings. Furthermore, a storage tank could have been added, which also could increase the savings as it would boost energy flexibility.

Disturbances, other than solar radiation and ambient temperatures, have been neglected in this study, for example, human activity. It is left as a point for future studies to include and assess the impact of building usage in the models and analysis.

6. Conclusions

The potential of achieving CO${}_2$ savings using the energy flexibility of buildings has been analysed in a range of relevant scenarios including, both a family house and an office building. The simulated buildings were heated with heat pumps and the characteristics were varied according to the historical development of Danish building codes. The CO${}_2$ level of the electricity generation for a year-long period in the Danish area DK2 was used as input, together with weather data from the area.

The results show considerable CO${}_2$ savings for both radiator and floor heating systems. Forecast horizons should be 24 h or longer to obtain the full savings potential. Over-dimensioning the heat pump to increase flexibility turns out only to yield significant savings with floor heating, especially in the office building due to its larger storage area relative to the wall area.

Complying with BC${}_{2015:2018}$ requirements, savings can reach around 17% using floor heating with 200 mm of floor concrete and 12% using radiators (Table 3). Generally, buildings must comply with building codes later than 1977 to achieve any considerable savings due to the low requirements in BC${}_{1977}$.

Predictive control is vital to eliminate the peak hours, especially happening in the morning after the nightly setback, which is common practise. It is able to shift the demand to periods, where the coal power production is low, typically out of cooking peaks and during night time.