Cost-Aware Design and Simulation of Electrical Energy Systems
Abstract
:1. Introduction
2. Background
2.1. Cost Estimation for EES Systems
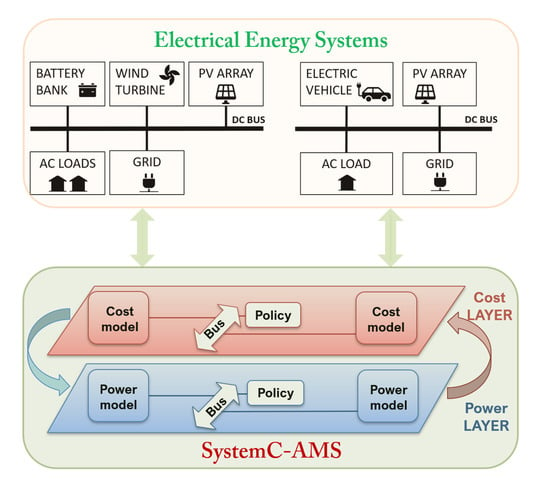
2.2. A Multi-Layered Approach for Functional and Extra-Functional Simulation
3. Modeling of Cost
3.1. Main Characteristics of the Cost Layer
- Each component computes its “local” costs over time;
- All individual costs are conveyed to the cost bus;
- The cost bus estimates additional global costs, i.e., due to energy balance with respect to the grid;
- The cost bus determines and keeps track of the total balance over time.
3.2. Cost Models
3.2.1. Component-Specific Costs
Initial Capital Cost
Time-Dependent Capital Cost
Operation and Maintenance Cost
3.2.2. Bus Models
Electricity Cost
Net Cost
Annualized Cost
Profit
3.3. Interaction with the Power Layer
- The time-dependent capital cost requires information about the current loss of functionality of the component L, and the maximum accepted loss (Equation (4)). Both values are known at the power layer: is a configuration value used by policies to determine when the component reached the end of its lifetime; L is a value that is constantly updated at simulation time to correctly estimate the behavior of the component. Using again the example of a battery, this would be approximated by the full cycle equivalent [41], i.e., the number of equivalent full charge-discharge cycles, which can be computed by just knowing the nominal battery capacity and the instantaneous power drawn.
- The operation and maintenance cost strictly depends on the power produced or stored by a component over a given time interval (Equation (5)); the power layer naturally keeps track of this quantity during simulation.
- The energy balance over time , taking into account the difference between the power provided by power sources and the power demand to guarantee the load operations. This quantity allows one to compute the electricity cost over time (Equation (6));
- The total power produced over time by power sources , useful for the estimation of the annualized cost (Equation (8)).
- The current price of electricity: at times, the price of electricity may be so low that it makes convenient to recharge all energy storage elements (e.g., battery packs), and use the stored energy to power the system when electricity price is higher.
- Data on wear-out and/or depreciation in the form of alarms or warnings that can be used to force the replacement of some components.
4. SystemC-AMS Implementation
4.1. SystemC-AMS
4.2. SystemC-AMS Implementation of the Proposed Solution
5. Simulation Results
5.1. EES Case Study 1
5.1.1. Power Layer
- The wind turbine is modeled with a mechanical model, proposed in [47];
- The PV array is modeled with a model of a single PV module, built by adopting the solution in [48], scaled up to the size of the PV array;
- The battery pack is based on the circuit-equivalent model in [38] (which models a single battery cell), scaled up to the size of the pack;
- AC loads reproduce power consumption of a residential community including 15 houses [49];
- Converters are modeled in terms of their conversion efficiency as introduced in [50];
- The grid component is used only to keep track of the power balance between demand and supply, and of any inefficiency introduced by the presence of a transformer between the grid and the power bus.
5.1.2. Cost Layer
- The wind turbine and the PV array are considered as fixed lifetime components (with lifetime 20 years, as derived from their datasheets); thus, their time-dependent capital is modeled as in Equation (2).
- The battery pack has a variable lifetime, depending on its usage profile; thus, its time-dependent capital cost is modeled as in Equation (4), by considering the loss of functionality L as a aging degradation of battery capacity over time. The state of health (SOH) of the battery pack is represented by .
5.1.3. One-Month Example Simulation Traces
Evolution of the Power Layer
Evolution of the Cost Layer
Evolution of Component-Specific Costs
Comparisons with Previous Works
5.1.4. Design Space Exploration through Proposed Simulation Framework
Comparison of Different Power Bus Policies
Exhaustive Exploration of Different Configurations
- The number of PV modules varies from 0 to 100 in steps of 10 when the wind turbine is present, and from 0 to 150 when there is no wind turbine in the EES;
- The number of battery cells varies from 0 to 10,000, in steps of 1000.
Exploration with Fixed Initial Capital Cost
5.2. EES Case Study 2
5.2.1. One-Week Example Simulation Traces
Evolution of the Power Layer
Evolution of the Cost Layer
5.2.2. Comparison of Different EVs in the EES
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Ref. | Goal | Energy Models | Cost Models | Proposed Solution |
|---|---|---|---|---|
| [13] | Optimize energy storage configuration to minimize fuel costs | Simple linear models, e.g., PV power as function of area and rated power | Operation and maintenance, replacement, capital | Comparison of alternative configurations |
| [14] | Find sizing of EES components that minimizes levelized cost of electricity | Based on linear equations of rated power and capacity | Capital, operation and maintenance, replacement | HOMER [58] and artificial bee colony optimization |
| [15] | Optimal configuration while minimizing total net present cost | Simplified models of EES components (e.g., battery as a function of efficiency and depth of discharge) | Capital, replacement, operation and maintenance | Hybrid optimization genetic algorithm |
| [16] | Optimization of levelized energy cost and payback time, emission reduction | Simple linear models | Annual investment and replacement, emission reduction benefit | Particle swarm optimization to identify optimal component sizing |
| [17] | Minimize cost and improve reliability | Simple linear models, e.g., power sources as linear function of environmental quantity | Investment, replacement, operation and maintenance, electricity | Constrained optimization problem to determine capacity of power sources and storage |
| [18] | Optimization of annualized cost through dimensioning of EES components | Power sources as simple linear function of environmental quantities | Operation and maintenance, capital, replacement, electricity | Mixed integer linear programming applied to different scenarios |
| [19] | Optimal sizing of EES components to minimize levelized cost of energy | Accurate models, fixed power management policy | Capital, operation and maintenance, replacement | Genetic algorithm |
| [20] | Maximize electricity bill savings with optimal sizing of energy storage | Accurate model only of energy storage devices | Capital, electricity, replacement | Non-convex optimization problem plus exhaustive-search solution |
| [21] | Optimal sizing of EES components given pricing policies | Focus only on power source capacity and battery state of charge | Capital, operation and maintenance, electricity | Cataclysm genetic algorithm |
| [22] | Reduce cost of microgrid expansion considering impact of battery dynamics | Focuses on batteries, simple model of power sources | Capital, electricity, annualized cost | Mixed integer linear programming |
| [23] | Optimize battery sizing given battery bank degradation cost | Models only battery aging, fixed power management policy | Electricity, battery degradation | Linear optimization method |
| [24] | Optimize battery size and scheduling taking into account costs and loads | Simple linear models, input traces for power sources | Electricity, battery capital cost | Convex programming method |
| [25] | Find sizing of EES components plus operating strategy to minimize costs | Simple models, based on rated power, efficiency coefficients, area occupied by PV modules, etc. | Annualized system cost | Mixed integer linear programming model solved with CPLEX |
| [26] | Optimization of battery management to minimize electricity cost and carbon dioxide emissions | Focuses on battery state of charge, no model of other EES components | Electricity, emissions equivalent cost | Multi-objective optimization (energy cost and emissions) |
| [27] | Co-scheduling problem of HVAC control and battery management | Detailed model only of batteries (power sources as input traces, converters as efficiency coefficients) | Electricity, battery degradation | Minimize total cost with the convex optimization tool CVX |
| [28] | Utility scheduling to minimize total operational cost | Storage devices modeld only as their lifetime, power sources as input traces | Electricity, degradation, pricing schemes | Nonlinear mixed integer optimization to determine schedule of batteries and supercapacitors |
| [29] | Determine optimal power management policy to reduce operation and emission costs | EES components as min-max constraints for the optimization | Operation and maintenance, electricity | Particle swarm optimization |
| [30] | Balance total power generation w.r.t. load and minimize total operation cost | Capacity and scheduling as goal of optimization | Capital, operation and maintenance, electricity | Integer linear programming with CPLEX |
| [31] | Construction of optimal scheduling to optimize usage of storage and grid | EES capacity as constraints and object of optimization | Levelized cost of energy | Predictive optimization given a graph of alternatives |
| [32] | Techno-economic model to determine optimal capacity of PV system and battery storage | Simple models, e.g., PV as linear function of irradiance and temperature | Capital, operation, payback time | Particle swarm optimization |
| [33] | Optimal sizing of EES components to maximize profit | Accurate model only of PV modules | Capital, operation and maintenance, electricity | Dynamic simulation to evaluate impact of electricity tariffs |
| [34] | Feasibility study of wind/PV hybrid system | Accurate model only for PV modules | Capital, operation and maintenance, replacement | Simulation based on MATLAB and HOMER [58] |
| [35] | Operation cost minimization with different pricing mechanisms | Simple linear models | Annualized cost of system components | Based on HOMER [58] |
| This | Estimate mutual impact of power dynamics and costs to reach effective design of EES (Section 3.3 and Section 5) | Level of detail can be tuned by user, allows one to have high level of accuracy of component dynamics (Section 2.2 and Section 4) | Capital, profit, depreciation, operation and maintenance, electricity, net and annualized cost (Section 3) | Simulation-based, allows efficient construction and evaluation of alternative configurations (Section 5) |
References
- Ahadi, A.; Liang, X. A stand-alone hybrid renewable energy system assessment using cost optimization method. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 376–381. [Google Scholar]
- Zhu, D.; Yue, S.; Park, S.; Wang, Y.; Chang, N.; Pedram, M. Cost-effective design of a hybrid electrical energy storage system for electric vehicles. In Proceedings of the International Conference on Hardware/Software Codesign and System Synthesis (CODES-ISS), New Delhi, India, 12–17 October 2014; pp. 1–8. [Google Scholar]
- Nelson, D.; Nehrir, M.; Wang, C. Unit sizing of stand-alone hybrid wind/PV/fuel cell power generation systems. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 16 June 2005; pp. 2116–2122. [Google Scholar]
- Shi, X.; Li, Y.; Cao, Y.; Tan, Y. Cyber-physical electrical energy systems: Challenges and issues. CSEE J. Power Energy Syst. 2015, 1, 36–42. [Google Scholar] [CrossRef]
- Ilic, M.D.; Xie, L.; Khan, U.A.; Moura, J.M. Modeling future cyber-physical energy systems. In Proceedings of the IEEE Power and Energy Society General Meeting, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–9. [Google Scholar]
- Al Faruque, M.A.; Ahourai, F. A model-based design of cyber-physical energy systems. In Proceedings of the IEEE Asia and South Pacific Design Automation Conference (ASP-DAC), Singapore, 20–23 January 2014; pp. 97–104. [Google Scholar]
- Kim, Y.; Shin, D.; Petricca, M.; Park, S.; Poncino, M.; Chang, N. Computer-aided design of electrical energy systems. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 18–21 November 2013; pp. 194–201. [Google Scholar]
- Molina, J.M.; Pan, X.; Grimm, C.; Damm, M. A framework for model-based design of embedded systems for energy management. In Proceedings of the IEEE Workshop on Modeling and Simulation of Cyber-Physical Energy Systems (MSCPES), Berkeley, CA, USA, 20–20 May 2013; pp. 1–6. [Google Scholar]
- Vinco, S.; Chen, Y.; Fummi, F.; Macii, E.; Poncino, M. A layered methodology for the simulation of extra-functional properties in smart systems. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2017, 36, 1702–1715. [Google Scholar] [CrossRef]
- Song, W.J.; Mukhopadhyay, S.; Yalamanchili, S. KitFox: Multiphysics Libraries for Integrated Power, Thermal, and Reliability Simulations of Multicore Microarchitecture. IEEE Trans. Compon. Packag. Manuf. Technol. 2015, 5, 1590–1601. [Google Scholar] [CrossRef]
- Fummi, F.; Lora, M.; Stefanni, F.; Trachanis, D.; Vanhese, J.; Vinco, S. Moving from co-simulation to simulation for effective smart systems design. In Proceedings of the Design, Automation Test in Europe Conference Exhibition (DATE), Dresden, Germany, 24–28 March 2014; pp. 1–4. [Google Scholar]
- Görgen, R.; Grüttner, K.; Herrera, F.; Peñil, P.; Medina, J.; Villar, E.; Palermo, G.; Fornaciari, W.; Brandolese, C.; Gadioli, D.; et al. Contrex: Design of embedded mixed-criticality control systems under consideration of extra-functional properties. In Proceedings of the 2016 Euromicro Conference on Digital System Design (DSD), Limassol, Cyprus, 31 August–2 September 2016; pp. 286–293. [Google Scholar]
- Gbadegesin, A.O.; Sun, Y.; Nwulu, N.I. Techno-economic analysis of storage degradation effect on levelised cost of hybrid energy storage systems. Sustain. Energy Technol. Assess. 2019, 36, 100536. [Google Scholar] [CrossRef]
- Singh, S.; Chauhan, P.; Aftab, M.; Ali, I.; Hussain, S.; Ustun, T. Cost Optimization of a Stand-Alone Hybrid Energy System with Fuel Cell and PV. Energies 2020, 13, 1295. [Google Scholar] [CrossRef] [Green Version]
- Fulzele, J.B.; Daigavane, M. Design and Optimization of Hybrid PV-Wind Renewable Energy System. Mater. Today Proc. 2018, 5, 810–818. [Google Scholar] [CrossRef]
- Mao, M.; Jin, P.; Chang, L.; Xu, H. Economic Analysis and Optimal Design on Microgrids With SS-PVs for Industries. IEEE Trans. Sustain. Energy 2014, 5, 1328–1336. [Google Scholar] [CrossRef]
- Akram, U.; Khalid, M.; Shafiq, S. An Innovative Hybrid Wind-Solar and Battery-Supercapacitor Microgrid System—Development and Optimization. IEEE Access 2017, 5, 25897–25912. [Google Scholar] [CrossRef]
- Atia, R.; Yamada, N. Sizing and Analysis of Renewable Energy and Battery Systems in Residential Microgrids. IEEE Trans. Smart Grid 2016, 7, 1204–1213. [Google Scholar] [CrossRef]
- Alramlawi, M.; Souidi, Y.; Li, P. Optimal design of PV-Battery Microgrid Incorporating Lead-acid Battery Aging Model. In Proceedings of the IEEE EEEIC/ICPS, Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar]
- Zhu, D.; Yue, S.; Chang, N.; Pedram, M. Toward a Profitable Grid-Connected Hybrid Electrical Energy Storage System for Residential Use. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2016, 35, 1151–1164. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, Y.; Lin, X.; Li, C.; Cai, Z.; Yang, P. Optimal Sizing of PV and BESS for a Smart Household Considering Different Price Mechanisms. IEEE Access 2018, 6, 41050–41059. [Google Scholar] [CrossRef]
- Alsaidan, I.; Khodaei, A.; Gao, W. A Comprehensive Battery Energy Storage Optimal Sizing Model for Microgrid Applications. IEEE Trans. Power Syst. 2018, 33, 3968–3980. [Google Scholar] [CrossRef]
- Hesse, H.; Martins, R.; Musilek, P.; Naumann, M.; Truong, C.; Jossen, A. Economic optimization of component sizing for residential battery storage systems. Energies 2017, 10, 835. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Yin, X.; Zhang, C.; Qian, S. Optimal battery sizing of smart home via convex programming. Energy 2017, 140, 444–453. [Google Scholar] [CrossRef]
- Luo, X.; Liu, Y.; Liu, J.; Liu, X. Optimal design and cost allocation of a distributed energy resource (DER) system with district energy networks: A case study of an isolated island in the South China Sea. Sustain. Cities Soc. 2019, 51, 101726. [Google Scholar] [CrossRef]
- Olivieri, Z.T.; McConky, K. Optimization of residential battery energy storage system scheduling for cost and emissions reductions. Energy Build. 2020, 210, 109787. [Google Scholar] [CrossRef] [Green Version]
- Cui, T.; Chen, S.; Wang, Y.; Zhu, Q.; Nazarian, S.; Pedram, M. Optimal co-scheduling of HVAC control and battery management for energy-efficient buildings considering state-of-health degradation. In Proceedings of the IEEE Asia and South Pacific Design Automation Conference (ASP-DAC), Macau, China, 25–28 January 2016; pp. 775–780. [Google Scholar]
- Ju, C.; Wang, P.; Goel, L.; Xu, Y. A Two-Layer Energy Management System for Microgrids With Hybrid Energy Storage Considering Degradation Costs. IEEE Trans. Smart Grid 2018, 9, 6047–6057. [Google Scholar] [CrossRef]
- Esfahanian, H.M.M.; Abtahi, A.; Zilouchian, A. Modeling a Hybrid Microgrid Using Probabilistic Reconfiguration under System Uncertainties. Energies 2017, 10, 1430. [Google Scholar]
- Lotfi, H.; Khodaei, A. Hybrid AC/DC microgrid planning. Energy 2017, 118, 37–46. [Google Scholar] [CrossRef]
- Gupta, N.; Francis, G.; Ospina, J.; Newaz, A.; Collins, E.G.; Faruque, O.; Meeker, R.; Harper, M. Cost Optimal Control of Microgrids Having Solar Power and Energy Storage. In Proceedings of the IEEE/PES Transmission and Distribution, Denver, CO, USA, 16–19 April 2018; pp. 1–9. [Google Scholar]
- Bandyopadhyay, S.; Chandra Mouli, G.R.; Qin, Z.; Elizondo, L.R.; Bauer, P. Techno-economical Model based Optimal Sizing of PV-Battery Systems for Microgrids. IEEE Trans. Sustain. Energy 2019, 1. [Google Scholar] [CrossRef]
- Buonomano, A.; Calise, F.; d’Accadia, M.D.; Vicidomini, M. A hybrid renewable system based on wind and solar energy coupled with an electrical storage: Dynamic simulation and economic assessment. Energy 2018, 155, 174–189. [Google Scholar] [CrossRef]
- Ramli, M.A.; Hiendro, A.; Al-Turki, Y.A. Techno-economic energy analysis of wind/solar hybrid system: Case study for western coastal area of Saudi Arabia. Renew. Energy 2016, 91, 374–385. [Google Scholar] [CrossRef]
- Khormali, S.; Niknam, E. Operation Cost Minimization of Domestic Microgrid under the Time of Use Pricing Using HOMER. In Proceedings of the Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 15–17 May 2019; pp. 1–6. [Google Scholar]
- Chen, Y.; Vinco, S.; Pagliari, D.J.; Montuschi, P.; Macii, E.; Poncino, M. Modeling and Simulation of Cyber-Physical Electrical Energy Systems with SystemC-AMS. IEEE Trans. Sustain. Comput. 2020, 1. [Google Scholar] [CrossRef]
- Capital Recovery Factor. 2018. Available online: https://www.homerenergy.com/products/pro/docs/latest/capital_recovery_factor.html (accessed on 6 June 2020).
- Chen, Y.; Macii, E.; Poncino, M. A circuit-equivalent battery model accounting for the dependency on load frequency. In Proceedings of the Design, Automation Test in Europe Conference (DATE), Lausanne, Switzerland, 27–31 March 2017; pp. 1177–1182. [Google Scholar]
- Bocca, A.; Chen, Y.; Macii, A.; Macii, E.; Poncino, M. Aging and Cost Optimal Residential Charging for Plug-In EVs. IEEE Des. Test 2017, 35, 16–24. [Google Scholar] [CrossRef]
- Lambert, T.; Gilman, P.; Lilienthal, P. Micropower System Modeling With Homer. In Integration of Alternative Sources of Energy; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Baek, D.; Chen, Y.; Chang, N.; Macii, E.; Poncino, M. Optimal Battery Sizing for Electric Truck Delivery. Energies 2020, 13, 709. [Google Scholar] [CrossRef] [Green Version]
- IEEE. Standard for Standard SystemC Analog/Mixed-Signal Extensions Language Reference Manual; Std 1666.1-2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–236. [Google Scholar]
- Chen, Y.; Vinco, S.; Macii, E.; Poncino, M. SystemC-AMS thermal modeling for the co-simulation of functional and extra-functional properties. ACM Trans. Des. Autom. Electron. Syst. TODAES 2018, 24, 1–26. [Google Scholar] [CrossRef]
- Unterrieder, C.; Huemer, M.; Marsili, S. SystemC-AMS-based design of a battery model for single and multi cell applications. In Proceedings of the PRIME Conference on Ph.D. Research in Microelectronics Electronics, Aachen, Germany, 12–15 June 2012; pp. 1–4. [Google Scholar]
- Vinco, S.; Sassone, A.; Fummi, F.; Macii, E.; Poncino, M. An open-source framework for formal specification and simulation of electrical energy systems. In Proceedings of the IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED), La Jolla, CA, USA, 11–13 August 2014; pp. 287–290. [Google Scholar]
- Kim, S.K.; Jeon, J.H.; Cho, C.H.; Ahn, J.B.; Kwon, S.H. Dynamic modeling and control of a grid-connected hybrid generation system with versatile power transfer. IEEE Trans. Ind. Electron. 2008, 55, 1677–1688. [Google Scholar] [CrossRef]
- Ohyama, K.; Nakashima, T. Wind turbine emulator using wind turbine model based on blade element momentum theory. In Proceedings of the IEEE Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Pisa, Italy, 14–16 June 2010; pp. 762–765. [Google Scholar]
- Vinco, S.; Chen, Y.; Macii, E.; Poncino, M. A unified model of power sources for the simulation of electrical energy systems. In Proceedings of the Great Lakes Symposium on VLSI (GLSVLSI), Boston, MA, USA, 18–20 May 2016; pp. 281–286. [Google Scholar]
- Kelly, J.; Knottenbelt, W. The UK-DALE dataset, domestic appliance-level electricity demand and whole-house demand from five UK homes. Sci. Data 2015, 2, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Baek, D.; Kim, J.; Di Cataldo, S.; Chang, N.; Macii, E.; Vinco, S.; Poncino, M. A systemc-ams framework for the design and simulation of energy management in electric vehicles. IEEE Access 2019, 7, 25779–25791. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory (NREL). Measurement and Instrumentation Data Center. Available online: https://midcdmz.nrel.gov/ (accessed on 6 June 2020).
- Liu, N.; Yu, X.; Wang, C.; Li, C.; Ma, L.; Lei, J. Energy-Sharing Model With Price-Based Demand Response for Microgrids of Peer-to-Peer Prosumers. IEEE Trans. Power Syst. 2017, 32, 3569–3583. [Google Scholar] [CrossRef]
- Magnani, S.; Pezzola, L.; Danti, P. Design optimization of a heat thermal storage coupled with a micro-CHP for a residential case study. Energy Procedia 2016, 101, 830–837. [Google Scholar] [CrossRef]
- Jabir, H.; Ishak, D.; Abunima, H. Impacts of Demand-Side Management on Electrical Power Systems: A Review. Energies 2018, 11, 1050. [Google Scholar] [CrossRef] [Green Version]
- Eid, C.; Koliou, E.; Valles, M.; Reneses, J.; Hakvoort, R. Time-based pricing and electricity demand response: Existing barriers and next steps. Util. Policy 2016, 40, 15–25. [Google Scholar] [CrossRef] [Green Version]
- Telaretti, E.; Dusonchet, L.; Massaro, F.; Mineo, L.; Pecoraro, G.; Milazzo, F. A simple operation strategy of battery storage systems under dynamic electricity pricing: An Italian case study for a medium-scale public facility. In Proceedings of the Renewable Power Generation Conference (RPG), Naples, Italy, 24–25 September 2014; pp. 1–7. [Google Scholar]
- Electric Vehicle (EV). 2019. Available online: https://batteryuniversity.com/learn/article/electric_vehicle_ev/ (accessed on 6 June 2020).
- Efficient, Informed Decisions about Distributed Generation and Distributed Energy Resources. 2018. Available online: https://www.homerenergy.com/ (accessed on 6 June 2020).

















| Component | Unit Rated Electric Characteristic | Cardinality (#) | Overall Rated Electric Characteristic |
|---|---|---|---|
| Wind Turbine | 10 kVA | 1 | 10 kVA |
| PV Module | 57 V 5.49 A | 30 | 10 kW |
| Battery Cell | 3400 mA 3.7 V | 40 × 60 | 200 Ah 144 V |
| Component | Unit Capital Cost ($) | O&M Cost ($/kW/Year) | Nominal Lifetime |
|---|---|---|---|
| Wind Turbine | 19,500.00 | 15 | 20 Years |
| PV Module | 675.00 | 15 | 20 Years |
| Battery Cell | 2.50 | 10 | SOH |
| Operation | Rate | Value ($/kWh) | Time Slot of Day |
|---|---|---|---|
| Buying | F1 | 0.220 | 10 a.m.–3 p.m., 6 p.m.–9 p.m. |
| F2 | 0.215 | 7 a.m.–10 a.m., 3 p.m.–6 p.m., 9 p.m.–11 p.m. | |
| F3 | 0.200 | 11 p.m.–7 a.m. | |
| Selling | - | 0.030 | all day |
| Cost Type | Cost-Aware Policy ($) | Non Cost-Aware Policy ($) | |
|---|---|---|---|
| Electricity cost | Buy | 2445.34 | 1855.35 |
| Sell | −507.34 | −416.51 | |
| Own (provided by EES) | 9146.64 | 9736.63 | |
| Battery | Time-dependent capital cost | 470.86 | 662.14 |
| Operation and maintenance cost | 17.46 | 24.73 | |
| PV array | Time-dependent capital cost | 1903.35 | 1903.35 |
| Operation and maintenance | 55.88 | 55.88 | |
| Wind turbine | Time-dependent capital cost | 1832.79 | 1832.79 |
| Operation and maintenance cost | 123.57 | 123.57 | |
| Net Cost | 6341.97 | 6041.30 | |
| Profit | 2804.67 | 3695.33 | |
| Config. | PV Modules (#) | Batteris (#) | Wind Turbines (#) | Config. | PV Modules (#) | Batteries (#) | Wind Turbines (#) |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 16,200 | 1 | 11 | 50 | 2700 | 1 |
| 2 | 5 | 14,850 | 1 | 12 | 55 | 1350 | 1 |
| 3 | 10 | 13,500 | 1 | 13 | 60 | 0 | 1 |
| 4 | 15 | 12,150 | 1 | 14 | 0 | 8400 | 2 |
| 5 | 20 | 10,800 | 1 | 15 | 5 | 7050 | 2 |
| 6 | 25 | 9450 | 1 | 16 | 10 | 5700 | 2 |
| 7 | 30 | 8100 | 1 | 17 | 15 | 4350 | 2 |
| 8 | 35 | 6750 | 1 | 18 | 20 | 3000 | 2 |
| 9 | 40 | 5400 | 1 | 19 | 25 | 1650 | 2 |
| 10 | 45 | 4050 | 1 | 20 | 30 | 300 | 2 |
| Year | Eugene, Oregon | Tucson, Arizona | Absolute Difference ($) | Relative Difference (%) | ||
|---|---|---|---|---|---|---|
| Config. | Profit ($) | Config. | Profit ($) | |||
| 1 | 19 | 2402.92 | 18 | 6062.42 | 3659.50 | 152.29% |
| 5 | 19 | 11,997.35 | 18 | 30,282.70 | 18,285.35 | 152.41% |
| 10 | 19 | 23,971.38 | 18 | 60,679.42 | 36,708.04 | 153.13% |
| 15 | 19 | 35,432.53 | 18 | 90,469.58 | 55,037.05 | 155.32% |
| 20 | 19 | 49,118.32 | 18 | 122,508.33 | 73,390.01 | 149.41% |
| EES No. | PV Modules Number | Electric Vehicle | |
|---|---|---|---|
| EV Model | Battery Pack Size (kWh) | ||
| 1 | 0 | NaN | 0 |
| 2 | 10 | NaN | 0 |
| 3 | 10 | Mitsubishi MiEV | 16 |
| 4 | 10 | GM Spark | 21 |
| 5 | 10 | Nissan Leaf | 30 |
| 6 | 10 | BMW i3 (2019) | 42 |
| 7 | 10 | Tesla S 60 | 30 |
| No. | Electricity Cost ($) | PV Array Cost ($) | Battery Pack Cost ($) | Net Cost ($) | Profit ($) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Buy | Own | Sell | Time- Dependent Capital Cost | O&M | Time- Dependent Capital Cost | O&M | |||
| 1 | 1513.08 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1513.08 | −1513.08 |
| 2 | 833.48 | 672.17 | 385.03 | 52.15 | 1.98 | 0.00 | 0.00 | 1097.27 | −425.11 |
| 3 | 812.71 | 689.20 | 385.03 | 52.15 | 1.98 | 20.58 | 0.10 | 1097.95 | −408.75 |
| 4 | 796.10 | 1051.30 | 385.03 | 52.15 | 1.98 | 445.34 | 2.09 | 1508.09 | −456.79 |
| 5 | 793.08 | 1087.52 | 385.03 | 52.15 | 1.98 | 477.59 | 2.30 | 1537.52 | −450.00 |
| 6 | 793.08 | 1087.52 | 385.03 | 52.15 | 1.98 | 471.80 | 2.30 | 1531.82 | −444.30 |
| 7 | 793.08 | 1087.52 | 385.03 | 52.15 | 1.98 | 467.80 | 2.30 | 1527.73 | −440.21 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Vinco, S.; Baek, D.; Quer, S.; Macii, E.; Poncino, M. Cost-Aware Design and Simulation of Electrical Energy Systems. Energies 2020, 13, 2949. https://doi.org/10.3390/en13112949
Chen Y, Vinco S, Baek D, Quer S, Macii E, Poncino M. Cost-Aware Design and Simulation of Electrical Energy Systems. Energies. 2020; 13(11):2949. https://doi.org/10.3390/en13112949
Chicago/Turabian StyleChen, Yukai, Sara Vinco, Donkyu Baek, Stefano Quer, Enrico Macii, and Massimo Poncino. 2020. "Cost-Aware Design and Simulation of Electrical Energy Systems" Energies 13, no. 11: 2949. https://doi.org/10.3390/en13112949
APA StyleChen, Y., Vinco, S., Baek, D., Quer, S., Macii, E., & Poncino, M. (2020). Cost-Aware Design and Simulation of Electrical Energy Systems. Energies, 13(11), 2949. https://doi.org/10.3390/en13112949