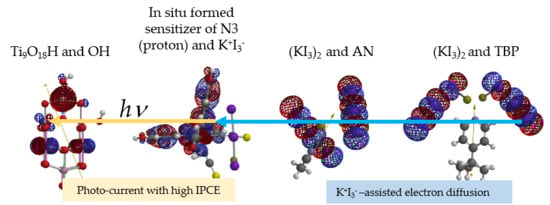
Density Functional Theory-Based Molecular Modeling: Verification of Decisive Roles of Van der Waals Aggregation of Triiodide Ions for Effective Electron Transfer in Wet-Type N3-Dye-Sensitized Solar Cells

Abstract

Density functional theory-based molecular modeling (DFT/MM) validates that KI and I₂ undergo exothermic van der Waals (vdW) aggregation in acetonitrile (AN) or in the presence of 4-tert-butylpyridine (TBP), forming potassium triiodide (KI₃) and, further mutual vdW aggregation leads to the formation of (KI₃)₂ and AN, (KI₃)₂ and (AN)₂ and (KI₃)₂ and TBP in the AN-based Dye sensitized solar cells (DSSC) electrolytes. All KI₃ aggregates have a very low energy gap, 0.17 eV, 0.14 eV and 0.05 eV of lowest unoccupied molecular orbital (LUMO) + 1 and LUMO, respectively, verifying efficient electron diffusion in μm-thick DSSC electrolytes. Hydrogen-bonding aggregation of anatase TiO₂ model, Ti₉O₁₈H and OH, with N3 (proton) dye is also validated by DFT/MM, and the energy structure verifies unidirectional electron flow from highest occupied molecular orbital (HOMO) on thiocyanide (SCN) groups of N3 dye to LUMO on the TiO₂ model at the aggregates. Further, DFT/MM for the aggregation of K⁺I₃⁻ with N3 verifies the most exothermic formation of the aggregate of N3 (proton) and K⁺I₃⁻. The UV-Vis spectra of N3 (proton) and K⁺I₃⁻ is consistent with reported incident photocurrent efficiency (IPCE) action spectra (λ = 450–800 nm) of N3-sensitized DSSC, verifying that the N3 dye of N3 (proton) and K⁺I₃⁻ becomes an effective sensitizer in the anode / TiO₂ / N3 (proton) / KI/I₂ / acetonitrile (AN) / cathode structured DSSC. The energy structure of LUMO and LUMO + 1 of the aggregates, Ti₉O₁₈H and OH and N3 (proton), N3 and K⁺I₃⁻, (KI₃)₂ and AN and (KI₃)₂ and TBP verifies high IPCE photocurrent and effective electron diffusion via KI₃-aggregates in the DSSC of Ti₉O₁₈H and OH and N3 (proton) and K⁺I₃⁻.

1. Introduction

As reported in the preceding papers [1,2,3,4,5,6], quantum chemistry molecular modeling, i.e., density functional theory-based molecular modeling (DFT/MM) can be regarded as theory-based “experiments”. DFT/MM can be carried out very quickly using high-end supercomputer-like personal computers. DFT/MM are applicable to molecular aggregates which are induced by van der Waals (vdW) force (including hydrogen bonding and Coulomb interactions). DFT/MM for the structuring of aggregates gives the heat of formation, dipole moment for understanding solubility in polar solvent like water and acetonitrile (AN) and the energy structures of aggregates, i.e., surface orbital electron energy structures [almost degenerate highest molecular orbitals [HOMO (n), n = 0–4)] and the lowest unoccupied molecular orbitals [LUMO + n, n = 0–2)]. Their molecular orbital configurations are evaluated as theory-based “experimental” data for verification and prediction of interacting molecules. Semiconducting property of the aggregates can be verified by the orbital energy gap between LUMO and LUMO + 1 [2,3]. We performed DFT/MM using the B3LYP exchange correlation functional and the 6–31G(d) basis set with Spartan’18 (Wavefunction, Inc. Irvine, CA). Prior to the DFT calculation for electronic properties, the geometries of the molecular aggregates were determined by the molecular mechanics employing the Merck molecular force field (MMFF).

Since the first report of its high-performance by O’Regan and Grätzel [7], the dye-sensitized solar cell (DSSC) using KI / I₂ / acetonitrile electrolyte has been a focus for a fundamental understanding of microscopic electronic phenomena of TiO₂, dye molecules and electrolytes [8]. As for wet-type DSSC electrolytes of acetonitrile (AN), KI and I₂, redox couple of I^−/I₃⁻was introduced to explain electron diffusion by electron hopping and exchange mechanisms [9]. Recently, we reported that DFT/MM verifies the semiconducting properties for quasi-solid state I₅⁻N(CH₃)₄⁺ -based electrolytes of DSSC [1]. In addition, we clarified that PbI₆⁴⁻/MeNH₃⁺ -based perovskite solar cells have excellent electron diffusion among panchromatic PbI₆⁴⁻/MeNH₃⁺ matrixes in the solar cells [2,3]. We have ascribed excellence of perovskite solar cells to PbI₆⁴⁻/MeNH₃⁺ -induced vdW aggregation. Here, we corroborate that the iodine element-based vdW aggregations also play an important role in unidirectional electron diffusion in wet-type DSSC using KI/I₂/acetonitrile electrolytes.

2. Results

2.1. DFT-Based Electrostatic Potential Map (EPM) and Van der Waals Aggregation

Figure 1 shows the EPM of I₂, KI, and AN.

In the colorful electrostatic potential map (ESPM), the property range (kJ/mol, eV) indicates potential energy of surface electron density of molecules and of vdW aggregates. Blue surface color is particularly electron poor and subject to electrophilic attack (electron poor vdW surface), and red surface color is particularly electron rich, subject to nucleophilic attack (electron rich vdW surface). As quantitative structured activity, volume (ų) of molecules is determined by the CPK model, reflecting surface electron number of molecules and aggregates. It may be added that the blue region corresponds to the LUMO rich region, and the red region to the HOMO rich region.

Pale blue EPM of I₂ indicates its electrophilic nature and the top surface is particularly electrophilic. Colorful EPM of KI and AN indicate the presence of both electrophilic and nucleophilic surface, reflecting large dipole, 10.68 debye and 3.81 debye, respectively. It is worth noting that the volumes of I₂ and KI are much larger than that of AN. Van der Waals aggregation occurs between electrophilic electron surface and nucleophilic one.

2.2. Verification of KI₃ Formation by Van der Waals Aggregation of I₂ and KI in Electrolytes

We speculate that the minimum number of molecules which may form vdW aggregates in AN should be three, and one of them is AN. Figure 2 shows ESPM of equilibrium geometry of vdW aggregates of (I₂)₂AN, (KI)₂AN, and acetonitrile (AN)₃. When compared to ESPM of I₂, and KI and AN in Figure 1, all of trimeric aggregates result from vdW aggregation between the electron-poor electrophilic surface and the electro-rich nucleophilic surface.

All vdW aggregates form exothermically, suggesting stability in AN. The most stable vdW aggregate of (KI)₂AN (heat of formation is −49.6 kcal/mol) gives a colorful ESPM, predicting further vdW aggregation with KI and I₂ in AN.

Figure 3 shows ESPM of I₂ and KI and AN, KI₃ and I₂ and KI, and KI₃ and (AN)₂. All vdW aggregates give large heat of formation and, interestingly, I₂ aggregates with KI in aggregate of I₂ and KI and AN. Geometry of I₃⁻ gives angle of 172° comparable to that of geometry I₃⁻ in KI₃ and (AN)₂. DFT/MM-determined UV-Vis spectrum comparison (λmax: 447 nm and 414 nm) verifies in situ formation of KI₃ from I₂ and KI in AN. In situ formation of KI₃ from I₂ and KI is also confirmed in vdW aggregate of KI₃ and I₂ and KI.

2.3. Van der Waals Aggregation of Potassium Triiodide (KI₃) and 4-Tertbyutylpyridine (TB) Effect on DSSC Electrolytes

Interestingly, DFT/MM of vdW aggregate of KI₃ and I₂ and KI reveals that the energy gap of ELUMO + 1 and ELUMO is 0.19 eV, predicting that the aggregate is semiconducting once it is formed. With this prediction in mind, DFT/MM is extended to vdW aggregates of (KI₃)₂ and AN, and of (KI₃)₂ and (AN)₂ to clarify the reason why the electrolyte of KI /I₂ /AN become semiconducting. In addition, since it is well-known that presence of 4-tert-butylpyridine (TBP) in the electrolytes improves open circuit voltage (Voc) of DSSC. Open circuit voltage depends on electron leak-free unidirectional photocurrent [8,10]. DFT/MM is also extended to vdW aggregate of (KI₃)₂ and TBP.

Figure 4 shows the EPSM of equilibrium geometry of vdW aggregates of (KI₃)₂ and AN, (KI₃)₂ and (AN)₂, (KI₃)₂ and TBP. The heat of formation values verify exclusive formation of vdW dimer of KI₃ in wet type DSSC electrolytes. UV-Vis spectra support the orange color of the electrolytes. Energy gaps of LUMO + 1 and LUMO are all less than 0.2 eV, and their configurations explain unidirectional electron flow from LUMO + 1 to LUMO. Interestingly, the vdW aggregate of (KI₃)₂ and TBP gives the smallest energy gap of 0.05 eV.

In order to validate conductivity of electron-running state of the vdW aggregates of KI₃ -based electrolytes, EPM and energy structures of electron injected [(KI₃)₂ and AN]^.− and [(KI₃)₂ and TBP]^.− are examined (Figure 5). Reddish ESPM indicates nucleophilic surface state, both negative values of heat of their electron acceptance verify their electron acceptability, and hopping between them is favorable in the electrolytes. As for surface energy structures, Ea (HOMO) is identical with electron singly occupied molecular orbital (SOMO). Accepted electron (spin density) is located in bLUMO. We understand that spin may run on bLUMO at electron running process. The energy gap of bLUMO and SOMO (0.46 eV and 0.35 eV, respectively), is small enough for spin (unpaired electron) to run under irradiance of solar energy (hν).

2.4. Electrostatic Potential Map (ESPM) of TiO₂ Anatase Nanoparticle and Conductivity

Figure 6 shows the ESPM of anatase TiO₂ model of Ti₉O₁₈H and OH proposed by Jono and Yamashita (Jono-Yamashita model) [11]. The validity of the Jono-Yamashita model for TiO₂ nanoparticle (NP) has been confirmed elsewhere [12]. Colorful ESPM verifies that three-dimensional vdW aggregates may form TiO₂ thin films and result in giving porous structures when sintered at high temperature.

To understand the nature of electron acceptability and electron-transfer in TiO₂, electron running molecular orbital configurations of LUMO and LUMO + 1 are shown as the side view (a) and the view from the top (b) of the TiO₂ model. The energy gap of LUMO + 1 and LUMO is 0.43 eV, which verifies and predicts that TiO₂ model and their vdW aggregates become semiconducting when LUMO and LUMO + 1 accept photoelectron.

2.5. Electrostatic Potential Map (ESPM) of Sensitizing N3 Dyes and Perspective of Van der Waals Aggregation

Figure 7 shows ESPM of two kinds of N3 (tetramethylammonium) (a homolog of N719) and N3 (proton) with UV-Vis spectra and electron energy structures. Colorful ESPM suggests that they are likely not to aggregate each other, but orange-colored SCN group sites may be vdW-aggregated by electrophilic potassium triiodide (K⁺I₃⁻). Each energy gap of LUMO + 1 and LUMO, 0.36 eV and 0.10 eV predicts that both N3 dyes are conductive.

Recently we reported that DFT/MM predict that DFT/MM-determined UV-Vis absorption spectra are strongly affected by vdW aggregation with other molecules, which was exemplified by UV-Vis spectrum of benzene solution [3]. Figure 7 reveals that DFT/MM-based UV-Vis spectrum of N3 (tetramethylammonium) is quite comparable to the incident photocurrent efficiency (IPCE) action spectra of N3-sensitized DSSC [13]. However, UV-Vis spectrum of N3 (proton) gives 380 nm red shifted one with decreased strength of absorption. DFT/MM-determined three-dimensional molecular structures verify that the difference comes from a change of coordination structure of ligands, bipyridyl and SCN ligands around Ru(II) ion (see Section 3).

2.6. Verification of Van der Waals Aggregation of N3 Dye with Anatase TiO₂ Model

Here, let us consider vdW aggregation of anatase TiO₂ and N3 dye molecule, which may allow us to gain insights into the electronic natures of the TiO₂ /N3 (proton) dye interface in DSSC. The problem of dye-anchoring on anatase TiO₂ had been argued several times in the past, e.g., ester formation with bipyridyl carboxylic acid ligand (bpy-dca), coordination of the bipyridyl ligand to Ti(IV), and hydrogen bonding with the bipyridyl ligand [14,15,16]. DFT/MM now verifies that N3 dye can be anchored by van der Waals force of hydrogen bonding between the hydroxyl group on TiO₂ and the carboxyl group of N3 dye (Figure 8). Heat of formation of −13.1 kcal/mol is not large enough to form strong vdW aggregation. We failed to obtain UV-Vis absorption spectra of the aggregate. However, surface electron energy structures, EHOMO and ELUMO and their configurations verify that photoexcitation of N3 dye induces electron injection from HOMO’s on SCN ligands to LUMO’s on anatase TiO₂.

2.7. Van der Waals Aggregation of N3 Dye with Potassium Triiodide

Remarkable vdW aggregation power of in situ formed potassium triiodide works on N3 (proton) dye molecules (Figure 9). Formation of vdW-aggregate of N3 (proton) and (KI₃)₂ and of N3(proton) and K⁺I₃⁻ are both exothermic (ΔE = −79.7 kcal/mol and ∆E = −142 kcal/mol respectively) and UV-Vis absorption maxima shift from near IR region to visible region. Interestingly, the UV-Vis spectra of the KI aggregates are consistent with reported IPCE action spectra (λ = 600–700 nm) of N3-sensitized DSSC [13].

The most stabilized vdW aggregate of N3 (proton) and K⁺I₃⁻ can be regarded as a new type of triiodide aggregated ruthenium dye. DFT/MM assigns the absorption maximum to molecular orbital components. All of them are regarded as results of photoexcitation from HOMO’s on SCN ligands to LUMO’s on bipyridyl ligands (Figure 10).

3. Discussion

Photoconversion efficiency (η) of solar cells of DSSC is determined by the following Equation:

η = J_sc × V_oc × ff / E

(1)

where J_sc is the short circuit photocurrent, V_oc is the open circuit voltage, ff is fill factor and E is solar energy 100 mW/cm².

Nazeeruddin, who invented a series of N3 dyes, reported that N3-dye-sensitized DSSC give J_sc = 16.8–19.0 mA/cm², V_oc = 600–770 mV, and ff 0.65–0.72, and photoconversion efficiency (η) at AM 1.5, 7.4–9.3%. In addition, he successfully measured excellent IPCE spectra (λ = 500–630 nm (70–80%)) of DSSC sensitized by respective N3 (proton) and N3 (tetrabutylammonium) (N719) [13].

In Figure 11, DSSC key components, anatase TiO₂ model, in situ-formed I₃⁻ -aggregated N3 dye of N3 and K⁺I₃⁻, KI₃-dimer aggregates, (KI₃)₂ and AN, and (KI₃)₂ and TBP, are aligned referring to the electrostatic potential map (ESPM). The pale green colored ESPM of (KI₃)₂ and AN, and (KI₃)₂ and TBP predict further vdW aggregation. Especially, vdW aggregation between N3 and K⁺I₃⁻, and (KI₃)₂ and AN or (KI₃)₂ and TBP is apparent in view of ESPM.

The above-mentioned high V_oc = 0.6–0.77 mV and the fill factors 0.65–0.72 of DSSC are validated as follows: Photo-formed electron runs through degenerate LUMO and LUMO + 1. Each LUMO + 1 and LUMO configuration visualize effective electron transfer in DSSC devices by following comparable potential energy of the KI₃-assisted aggregates (Figure 11).

Photoelectron on irradiated Ti₉O₁₈H and OH and N3 (proton) has a potential from −3.22 eV to −3.53 eV and transfer to LUMO + 1 and LUMO with potential from −4.20 eV to −4.63 eV. Photoelectron may have potential energy of 0.98–1.1 eV on anode to cathode. In general, clear-cut V_oc becomes measurable by effective electron transfer via electrolytes of (KI₃)₂ and AN, and of (KI₃)₂ and TBP. The measured V_oc = 0.6–0.77 mV is less than theoretical ones of 0.98–1.1 eV, and means that photoelectron leakage is not suppressed enough on N3-anchored TiO₂ NP electrodes. Improved conductivity of (KI₃)₂ and TBP (energy gap: 0.05 eV) is consistent with enhancement of conversion efficiency of solar cells.

The IPCE action spectrum ranges are 350–800 nm; at 350 nm (about 50%), at 500–630 nm (70–80%) and at 800 nm (about 5%) [13]. The excellent IPCE action spectra for N3-sensitized DSSC is now validated theoretically due to effective visible light-absorption of N3 and K⁺I⁻ dyes on porous TiO₂ films.

Figure 12 shows a comparison of the UV-Vis spectra of N3 (proton), N3 and K⁺I₃⁻, and N3 (tetramethylammonium) as a homologue of N719. UV-Vis allowed transition occurs between highest occupied molecular orbital (HOMO), HOMO − 1, and HOMO − 2 on SCN ligands to lowest unoccupied molecular orbital (LUMO), LUMO + 1, and LUMO + 2 on bpy-dca ligands. In addition, when the molecular structures are compared, the coordination structures of N3 and K⁺I₃⁻ and N3 (tetramethylammonium) are quite comparable, explaining that the respective 280 nm and 380 nm blue shift (bathochromic shift) comes from ligand-coordination change induced by vdW and Coulomb interaction of N3 with I₃⁻ and tetramethylammonium. The hyperchromic effect of increase of strength (ε) and the bathochromic effect (the red shift) in absorption spectrum of N3 (tetramethylammonium) validates that N719 is a respectable sensitizer of DSSC.

4. Conclusions

Experimental and theoretical UV-Vis spectral analyses of sensitizing dyes on TiO₂ NPs were not successful enough so far [17,18,19,20]. As we reported [3,5], Spartan (Q-Chem) (Wavefunction, Inc. Irvin. CA, USA) is a comprehensive ab-initio quantum-chemistry software for accurate predictions of molecular structures, reactivities, and vibrational, electronic and NMR spectra. We are very proud of the verification power of density functional theory-based molecular modeling (DFT/MM) using Spartan (involving Q-Chem), and now demonstrate that vdW aggregation power of triiodide ion contributes to solar light harvesting of N3 and effective electron diffusion in in situ formed triiodide ion-based electrolytes. The strong tendency of vdW aggregation via I₃⁻ at interfaces of DSSC facilitates DSSC fabrication with high performance of fill factor (ff) and respectable open circuit voltage (V_oc).

As a perspective conclusion, DFT/MM is a useful tool for verifying and predicting conductivity of electronic molecular aggregates, IPCE action spectra and theoretical V_oc of solar cells, as mentioned in the DFT/MM of perovskite solar cells [3].

During editing period of the article, we succeeded to obtain DFT/MM-based UV-Vis spectrum of van der Waals aggregate of N3(proton) with two acetonitrile (AN) molecules (see Supplementary).

It is now verified that the aggregation of N3 with AN, i.e. solvation of AN to N3, also affect energy structures of N3, giving four λmax: 692 nm (0.0008), 823 nm (0.0242), 875 nm (0.0164), 875 nm (0.0164). Compared to λmax of N3 (proton)K+I₃⁻, we conclude that the K⁺I₃⁻ aggregation to N3 is much more dramatic, causing favorable energy structure change of N3 (proton) followed by coordination geometry change.

5. Materials and Methods

The DFT-based MM with the SPARTAN’18 (Wavefunction, Inc. Irving, CA, USA) program code can be conducted by using high-end personal computers, deriving equilibrium geometries of van der Waals (vdW) aggregates such as I₂ and KI, and their aggregates with a Ru complex (N3 dye) and TiO₂ NP, along with the isosurface of the electrostatic potential based on the electronic charge distribution, thus helping us to gain insights into the nature of the iodine-based vdW bonds. Similar to the previous works [1,2,3,4,5,6], the DFT-based MM with B3LYP/6-31G(d) was employed to obtain the equilibrium geometry and electronic structure of vdW aggregates. Prior to the DFT calculation, the geometries of the molecular aggregates were determined by the molecular mechanics with the Merck molecular force field (MMFF) [21], so that the intermolecular vdW interaction and the electrostatic interaction was taken into account. The following calculation at the B3LYP/6-31G(d) level results in equilibrium geometry, van der Waals bonding is correctly described.

To simulate UV-Vis spectra revealing allowed electronic transitions with wavelength and intensity, we used the time-dependent DFT within the linear response regime [22,23]. The surface electron density and electrostatic potential map were used to elucidate molecular aggregation with vdW and electrostatic Coulomb interaction without covalent bonding. For a review of the quantum mechanical methods used in SPARTAN, see reference [24,25,26,27].