Near Real-Time Global Solar Radiation Forecasting at Multiple Time-Step Horizons Using the Long Short-Term Memory Network
Abstract
:1. Introduction
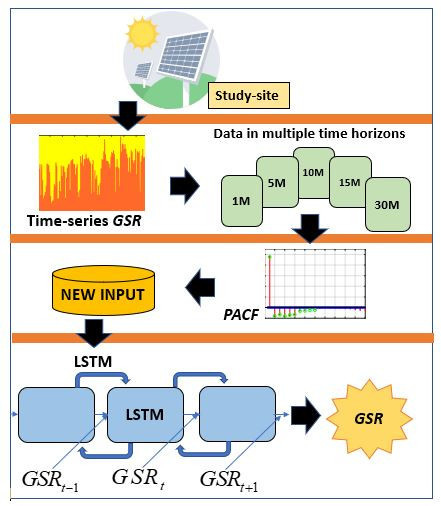
- Development and optimization of a near-real-time GSR forecasting method by implementing the LSTM algorithm for 1 min using lagged combinations of the aggregated GSR data as the predictor variables.
- Evaluation of the performance of the proposed model against benchmarked models (DNN, MLP, ARIMA, SVR) by a range of model evaluation metrics.
- Implementation of the proposed models for multi-minute ahead (e.g., 5 M, 10 M, 15 M, 30 M) and evaluation of the performance of LSTM over multiple forecast horizons.
2. Related Work
3. Theoretical Overview
3.1. Objective Predictive Model: Long Short-Term Memory (LSTM) Network
3.1.1. Computational Aspects of LSTM Network Model
3.1.2. Benchmark Model: Autoregressive Integrated Moving Average (ARIMA)
3.1.3. Benchmark Model: Support Vector Regression (SVR)
3.1.4. Benchmark Model: Deep Neural Network (DNN)
3.1.5. Benchmark Model: Multilayer Perceptron Network (MLP)
4. Materials and Method
4.1. Study Region
4.2. Data Preparation
4.3. LSTM Model Implementation
- Epoch defines the number of times that the learning algorithm will work through the entire training dataset. The number of epochs is usually hundreds or thousands, allowing the learning algorithm to run until the error from the learning model is minimized. In this study, the number of epochs is set to a maximum of 2000 (Table 4).
- Batch size defines the number of data points that are propagated through the network. The batch size can be seen as a for-loop iterating over one or more data points. At the end of each batch, the predicted values are compared to the actual values and the errors are calculated. From these errors, the update algorithm is used to improve the model. Depending on data length, to determine whether a greater batch size can provide the better performance, the batch size is set as in Table 3.
- Dropout is a regularization layer that blocks a random set of cell units in one iteration of LSTM training. Since over-fitting is prone during training, the dropout layer creates blocked units which can remove connections in the network. Therefore, it possibly decreases the number of free data points to be predicted and the complexity of the network. The dropout rate is often set between 0 and 1. In this study, this parameter was tested between two values, 0.1 and 0.2, to determine whether a greater value of dropout rate improves LSTM performance (Table 4a).
- Least absolute deviations and least square error (L1 and L2 regulation): In addition to dropout, the L1 and L2 regularization parameter is also used such that the L1 and L2 penalization parameter decreases the sum of absolute differences and the sum of square of differences between observed and forecasted values. In principle, adding a regularization term to the loss will facilitate a better network mapping (by penalizing large values of parameters which minimize the amount of nonlinearity of GSR values).
- Activation function: With the exception of the output layer, all the layers within a network typically use the same activation function known as the rectified linear unit (ReLU).
4.4. Benchmark Models Implementations
5. Model Performance Criteria
6. Statistical Significance Testing
7. Results and Discussion
8. Further Discussion, Limitations and Future Scope
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ACF | Autocorrelation |
| AR | Autoregressive |
| ARMA | Autoregressive Moving Average |
| ARIMA | Autoregressive Integrated Moving Average |
| FFNN | Feed Forward Neural Networks. |
| CPU | Central Processing Unit |
| d | Degree of differencing in ARIMA |
| DL | Deep Learning |
| DNN | Deep Neuron Network |
| GSR | Global Solar Radiation |
| Actual Global Solar Radiation | |
| Normalised Global Solar Radiation | |
| Maximum value of Global Solar Radiation | |
| Minimum value of Global Solar Radiation | |
| Observed Global Solar Radiation | |
| Average value of Observed Global Solar Radiation | |
| Forecasted Global Solar Radiation | |
| Average value of Forecasted Global Solar Radiation | |
| Nash-Sutcliffe Efficiency | |
| LM | Legate & McCabe’s Index |
| CNN | Convolutional Neural Network |
| NARX | Nonlinear autoregressive network with exogenous inputs |
| RBF | Radial Basis Function |
| ARIMAX | ARIMA with exogenous variables |
| LSTM | Long Short-Term Memory |
| MA | Moving Average |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MSE | Mean Squared Error |
| MLP | Multilayer Perceptron Network |
| PACF | Partial Auto-Correlation Function |
| p | Autoregressive term in ARIMA |
| Absolute Forecasted Error | |
| q | Moving average term in ARIMA |
| r | Pearson’s Correlation Coefficient |
| Coefficient of determination | |
| ReLU | Rectified Linear Unit |
| RMSE | Root Mean Square Error |
| RRMSE | Relative Root Mean Square Error |
| RNN | Recurrent Neural Networks |
| N | Number of values in a data series |
| SVR | Support vector regression |
| BPNN | Back-Propagation Neural Networks |
| ELM | Extreme Learning Machine |
| ANN | Artificial Neural Network |
| B-ELM | Bayesian extreme learning machine |
| RW | Rescorla–Wagner |
| ES | Evolution strategy |
References
- Färe, R.; Grosskopf, S.; Tyteca, D. An activity analysis model of the environmental performance of firms—Application to fossil-fuel-fired electric utilities. Ecol. Econ. 1996, 18, 161–175. [Google Scholar] [CrossRef]
- Agarwal, A.K. Biofuels (alcohols and biodiesel) applications as fuels for internal combustion engines. Prog. Energy Combust. Sci. 2007, 33, 233–271. [Google Scholar] [CrossRef]
- Ezra, D. Coal and Energy: The Need to Exploit the World’s Most Abundant Fossil Fuel; Wiley: Hoboken, NJ, USA, 1978. [Google Scholar]
- Amponsah, N.Y.; Troldborg, M.; Kington, B.; Aalders, I.; Hough, R.L. Greenhouse gas emissions from renewable energy sources: A review of lifecycle considerations. Renew. Sustain. Energy Rev. 2014, 39, 461–475. [Google Scholar] [CrossRef]
- Meinel, A.B.; Meinel, M.P. Applied solar energy: An introduction. NASA STI/Recon Tech. Rep. A 1977, 77, 33445. [Google Scholar]
- Luong, N.D. A critical review on energy efficiency and conservation policies and programs in Vietnam. Renew. Sustain. Energy Rev. 2015, 52, 623–634. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2016 Executive Summary; International Energy Agency: Paris, France, 2012. [Google Scholar]
- Shem, C.; Simsek, Y.; Hutfilter, U.F.; Urmee, T. Potentials and opportunities for low carbon energy transition in Vietnam: A policy analysis. Energy Policy 2019, 134, 110818. [Google Scholar] [CrossRef]
- Polo, J.; Bernardos, A.; Martínez, S.; Peruchena, C.F. Maps of Solar Resource and Potential in Vietnam; Ministry of Industry and Trade of the Socialist Republic of Vietnam: Hanoi, Vietnam, 2015.
- Al-Musaylh, M.S.; Deo, R.C.; Li, Y.; Adamowski, J.F. Two-phase particle swarm optimized-support vector regression hybrid model integrated with improved empirical mode decomposition with adaptive noise for multiple-horizon electricity demand forecasting. Appl. Energy 2018, 217, 422–439. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Qin, J.; Chen, Z.; Yang, K.; Liang, S.; Tang, W. Estimation of monthly-mean daily global solar radiation based on MODIS and TRMM products. Appl. Energy 2011, 88, 2480–2489. [Google Scholar] [CrossRef]
- Yang, H.-T.; Huang, C.-M.; Huang, Y.-C.; Pai, Y.-S. A weather-based hybrid method for 1-day ahead hourly forecasting of PV power output. IEEE Trans. Sustain. Energy 2014, 5, 917–926. [Google Scholar] [CrossRef]
- Pierro, M.; Bucci, F.; Cornaro, C.; Maggioni, E.; Perotto, A.; Pravettoni, M.; Spada, F. Model output statistics cascade to improve day ahead solar irradiance forecast. Sol. Energy 2015, 117, 99–113. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M. A 24-h forecast of solar irradiance using artificial neural network: Application for performance prediction of a grid-connected PV plant at Trieste, Italy. Sol. Energy 2010, 84, 807–821. [Google Scholar] [CrossRef]
- Alzahrani, A.; Shamsi, P.; Dagli, C.; Ferdowsi, M. Solar irradiance forecasting using deep neural networks. Procedia Comput. Sci. 2017, 114, 304–313. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Paulescu, E.; Blaga, R. Regression models for hourly diffuse solar radiation. Sol. Energy 2016, 125, 111–124. [Google Scholar] [CrossRef]
- Coulibaly, O.; Ouedraogo, A. Correlation of global solar radiation of eight synoptic stations in Burkina Faso based on linear and multiple linear regression methods. J. Sol. Energy 2016, 2016, 9. [Google Scholar] [CrossRef] [Green Version]
- Benmouiza, K.; Cheknane, A. Small-scale solar radiation forecasting using ARMA and nonlinear autoregressive neural network models. Theor. Appl. Climatol. 2016, 124, 945–958. [Google Scholar] [CrossRef]
- Sfetsos, A.; Coonick, A. Univariate and multivariate forecasting of hourly solar radiation with artificial intelligence techniques. Sol. Energy 2000, 68, 169–178. [Google Scholar] [CrossRef]
- Hocaoğlu, F.O. Stochastic approach for daily solar radiation modeling. Sol. Energy 2011, 85, 278–287. [Google Scholar] [CrossRef]
- Rigler, E.; Baker, D.; Weigel, R.; Vassiliadis, D.; Klimas, A. Adaptive linear prediction of radiation belt electrons using the Kalman filter. Space Weather 2004, 2, 1–9. [Google Scholar] [CrossRef]
- Bracale, A.; Caramia, P.; Carpinelli, G.; Di Fazio, A.; Ferruzzi, G. A Bayesian method for short-term probabilistic forecasting of photovoltaic generation in smart grid operation and control. Energies 2013, 6, 733–747. [Google Scholar] [CrossRef] [Green Version]
- Ming, D.; Ningzhou, X. A method to forecast short-term output power of photovoltaic generation system based on Markov chain. Power Syst. Technol. 2011, 35, 152–157. [Google Scholar]
- Wenbin, H.; Ben, H.; Changzhi, Y. Building thermal process analysis with grey system method. Build. Environ. 2002, 37, 599–605. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.; Alsamamra, H.; Tovar-Pescador, J.; Pozo-Vázquez, D. Proposal of a regressive model for the hourly diffuse solar radiation under all sky conditions. Energy Convers. Manag. 2010, 51, 881–893. [Google Scholar] [CrossRef]
- Martín, L.; Zarzalejo, L.F.; Polo, J.; Navarro, A.; Marchante, R.; Cony, M. Prediction of global solar irradiance based on time series analysis: Application to solar thermal power plants energy production planning. Sol. Energy 2010, 84, 1772–1781. [Google Scholar] [CrossRef]
- Moreno-Munoz, A.; De la Rosa, J.; Posadillo, R.; Bellido, F. Very short term forecasting of solar radiation. In Proceedings of the 2008 33rd IEEE Photovoltaic Specialists Conference, San Diego, CA, USA, 11–16 May 2008; pp. 1–5. [Google Scholar]
- Colak, I.; Yesilbudak, M.; Genc, N.; Bayindir, R. Multi-period prediction of solar radiation using ARMA and ARIMA models. In Proceedings of the 2015 IEEE 14th international conference on machine learning and applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 1045–1049. [Google Scholar]
- Rao, K.S.K.; Rani, B.I.; Ilango, G.S. Estimation of daily global solar radiation using temperature, relative humidity and seasons with ANN for Indian stations. In Proceedings of the 2012 International Conference on Power, Signals, Controls and Computation, Thrissur, Kerala, India, 3–6 January 2012; pp. 1–6. [Google Scholar]
- Kaplani, E.; Kaplanis, S. A stochastic simulation model for reliable PV system sizing providing for solar radiation fluctuations. Appl. Energy 2012, 97, 970–981. [Google Scholar] [CrossRef]
- Lauret, P.; Boland, J.; Ridley, B. Bayesian statistical analysis applied to solar radiation modelling. Renew. Energy 2013, 49, 124–127. [Google Scholar] [CrossRef]
- Ramedani, Z.; Omid, M.; Keyhani, A.; Shamshirband, S.; Khoshnevisan, B. Potential of radial basis function based support vector regression for global solar radiation prediction. Renew. Sustain. Energy Rev. 2014, 39, 1005–1011. [Google Scholar] [CrossRef]
- Nguyen, B.; Pryor, T. A computer model to estimate solar radiation in Vietnam. Renew. Energy 1996, 9, 1274–1278. [Google Scholar] [CrossRef]
- Nguyen, B.T.; Pryor, T.L. The relationship between global solar radiation and sunshine duration in Vietnam. Renew. Energy 1997, 11, 47–60. [Google Scholar] [CrossRef]
- Polo, J.; Gastón, M.; Vindel, J.; Pagola, I. Spatial variability and clustering of global solar irradiation in Vietnam from sunshine duration measurements. Renew. Sustain. Energy Rev. 2015, 42, 1326–1334. [Google Scholar] [CrossRef]
- Polo, J.; Bernardos, A.; Navarro, A.; Fernandez-Peruchena, C.; Ramírez, L.; Guisado, M.V.; Martínez, S. Solar resources and power potential mapping in Vietnam using satellite-derived and GIS-based information. Energy Convers. Manag. 2015, 98, 348–358. [Google Scholar] [CrossRef]
- Qin, W.; Wang, L.; Lin, A.; Zhang, M.; Xia, X.; Hu, B.; Niu, Z. Comparison of deterministic and data-driven models for solar radiation estimation in China. Renew. Sustain. Energy Rev. 2018, 81, 579–594. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Zhu, Z.; Gong, W.; Niu, Z.; Liu, H.; Liu, Z. Prediction of solar radiation in China using different adaptive neuro-fuzzy methods and M5 model tree. Int. J. Climatol. 2017, 37, 1141–1155. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Deo, R.C.; Cornejo-Bueno, L.; Camacho-Gómez, C.; Ghimire, S. An efficient neuro-evolutionary hybrid modelling mechanism for the estimation of daily global solar radiation in the Sunshine State of Australia. Appl. Energy 2018, 209, 79–94. [Google Scholar] [CrossRef]
- Kabir, E.; Kumar, P.; Kumar, S.; Adelodun, A.A.; Kim, K.-H. Solar energy: Potential and future prospects. Renew. Sustain. Energy Rev. 2018, 82, 894–900. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms. Appl. Energy 2019, 253, 113541. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Ryu, A.; Ito, M.; Ishii, H.; Hayashi, Y. Preliminary Analysis of Short-term Solar Irradiance Forecasting by using Total-sky Imager and Convolutional Neural Network. In Proceedings of the 2019 IEEE PES GTD Grand International Conference and Exposition Asia (GTD Asia), Bangkok, Thailand, 19–23 March 2019; pp. 627–631. [Google Scholar]
- Manohar, M.; Koley, E.; Ghosh, S.; Mohanta, D.K.; Bansal, R. Spatio-temporal information based protection scheme for PV integrated microgrid under solar irradiance intermittency using deep convolutional neural network. Int. J. Electr. Power Energy Syst. 2020, 116, 105576. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Liang, Z.; Wei, Z.; Sun, G. Hybrid method for short-term photovoltaic power forecasting based on deep convolutional neural network. IET Gener. Transm. Distrib. 2018, 12, 4557–4567. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Liu, C.; Yu, Y.; Pang, S.; Duić, N.; Shafie-Khah, M.; Catalao, J.P. Generative adversarial networks and convolutional neural networks based weather classification model for day ahead short-term photovoltaic power forecasting. Energy Convers. Manag. 2019, 181, 443–462. [Google Scholar] [CrossRef]
- Awan, S.M.; Khan, Z.A.; Aslam, M. Solar Generation Forecasting by Recurrent Neural Networks Optimized by Levenberg-Marquardt Algorithm. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 276–281. [Google Scholar]
- Mishra, S.; Palanisamy, P. Multi-time-horizon Solar Forecasting Using Recurrent Neural Network. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 18–24. [Google Scholar]
- Wang, M.; Zang, H.; Cheng, L.; Wei, Z.; Sun, G. Application of DBN for estimating daily solar radiation on horizontal surfaces in Lhasa, China. Energy Procedia 2019, 158, 49–54. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network. Appl. Energy 2019, 251, 113315. [Google Scholar] [CrossRef]
- Caballero, R.; Zarzalejo, L.F.; Otero, Á.; Piñuel, L.; Wilbert, S. Short term cloud nowcasting for a solar power plant based on irradiance historical data. J. Comput. Sci. Technol. 2018, 18, 186–192. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Cao, J.; Zhu, J. An LSTM Short-Term Solar Irradiance Forecasting Under Complicated Weather Conditions. IEEE Access 2019, 7, 145651–145666. [Google Scholar] [CrossRef]
- Mukherjee, A.; Ain, A.; Dasgupta, P. Solar Irradiance Prediction from Historical Trends Using Deep Neural Networks. In Proceedings of the 2018 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 12–15 August 2018; pp. 356–361. [Google Scholar]
- Lee, H.; Lee, B.-T. Bayesian deep learning-based confidence-aware solar irradiance forecasting system. In Proceedings of the 2018 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Korea, 17–19 October 2018; pp. 1233–1238. [Google Scholar]
- Zhou, H.; Zhang, Y.; Yang, L.; Liu, Q.; Yan, K.; Du, Y. Short-term photovoltaic power forecasting based on long short term memory neural network and attention mechanism. IEEE Access 2019, 7, 78063–78074. [Google Scholar] [CrossRef]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for solar power forecasting—An approach using AutoEncoder and LSTM Neural Networks. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 002858–002865. [Google Scholar]
- Wang, F.; Yu, Y.; Zhang, Z.; Li, J.; Zhen, Z.; Li, K. Wavelet decomposition and convolutional LSTM networks based improved deep learning model for solar irradiance forecasting. Appl. Sci. 2018, 8, 1286. [Google Scholar] [CrossRef] [Green Version]
- Muhammad, A.; Lee, J.M.; Hong, S.W.; Lee, S.J.; Lee, E.H. Deep Learning Application in Power System with a Case Study on Solar Irradiation Forecasting. In Proceedings of the 2019 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Okinawa, Japan, 11–13 February 2019; pp. 275–279. [Google Scholar]
- Siddiqui, T.A.; Bharadwaj, S.; Kalyanaraman, S. A deep learning approach to solar-irradiance forecasting in sky-videos. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; pp. 2166–2174. [Google Scholar]
- Lee, W.; Kim, K.; Park, J.; Kim, J.; Kim, Y. Forecasting solar power using long-short term memory and convolutional neural networks. IEEE Access 2018, 6, 73068–73080. [Google Scholar] [CrossRef]
- Srivastava, S.; Lessmann, S. A comparative study of LSTM neural networks in forecasting day-ahead global horizontal irradiance with satellite data. Sol. Energy 2018, 162, 232–247. [Google Scholar] [CrossRef]
- Gao, M.; Li, J.; Hong, F.; Long, D. Day-ahead power forecasting in a large-scale photovoltaic plant based on weather classification using LSTM. Energy 2019, 187, 115838. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, Y.; Mao, S.; Chen, X.; Zou, H. LASSO and LSTM integrated temporal model for short-term solar intensity forecasting. IEEE Internet Things J. 2018, 6, 2933–2944. [Google Scholar] [CrossRef]
- Zaouali, K.; Rekik, R.; Bouallegue, R. Deep learning forecasting based on auto-LSTM model for Home Solar Power Systems. In Proceedings of the 2018 IEEE 20th International Conference on High Performance Computing and Communications; IEEE 16th International Conference on Smart City; IEEE 4th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Exeter, UK, 28–30 June 2018; pp. 235–242. [Google Scholar]
- Deo, R.C.; Şahin, M.; Adamowski, J.F.; Mi, J. Universally deployable extreme learning machines integrated with remotely sensed MODIS satellite predictors over Australia to forecast global solar radiation: A new approach. Renew. Sustain. Energy Rev. 2019, 104, 235–261. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Tong, C.W.; Arif, M.; Petković, D.; Ch, S. A new hybrid support vector machine–wavelet transform approach for estimation of horizontal global solar radiation. Energy Convers. Manag. 2015, 92, 162–171. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep learning neural networks trained with MODIS satellite-derived predictors for long-term global solar radiation prediction. Energies 2019, 12, 2407. [Google Scholar] [CrossRef] [Green Version]
- Geurts, M. Time Series Analysis: Forecasting and Control. JMR J. Mark. Res. (pre-1986) 1977, 14, 269. [Google Scholar] [CrossRef]
- Ballabio, D.; Consonni, V.; Todeschini, R. The Kohonen and CP-ANN toolbox: A collection of MATLAB modules for self organizing maps and counterpropagation artificial neural networks. Chemom. Intell. Lab. Syst. 2009, 98, 115–122. [Google Scholar] [CrossRef]
- Hui, C.L.P. Artificial Neural Networks: Application; IntechOpen: London, UK, 2011. [Google Scholar]
- Martinez-Anido, C.B.; Botor, B.; Florita, A.R.; Draxl, C.; Lu, S.; Hamann, H.F.; Hodge, B.-M. The value of day-ahead solar power forecasting improvement. Sol. Energy 2016, 129, 192–203. [Google Scholar] [CrossRef] [Green Version]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef] [Green Version]
- Inman, R.H.; Pedro, H.T.; Coimbra, C.F. Solar forecasting methods for renewable energy integration. Prog. Energy Combust. Sci. 2013, 39, 535–576. [Google Scholar] [CrossRef]
- Raza, M.Q.; Nadarajah, M.; Ekanayake, C. On recent advances in PV output power forecast. Sol. Energy 2016, 136, 125–144. [Google Scholar] [CrossRef]
- Sivaneasan, B.; Yu, C.; Goh, K. Solar forecasting using ANN with fuzzy logic pre-processing. Energy Procedia 2017, 143, 727–732. [Google Scholar] [CrossRef]
- Golestaneh, F.; Pinson, P.; Gooi, H.B. Very short-term nonparametric probabilistic forecasting of renewable energy generation—With application to solar energy. IEEE Trans. Power Syst. 2016, 31, 3850–3863. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Venugopal, V.; Brandt, A.R. Convolutional neural network for short-term solar panel output prediction. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC)(A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa Village, HI, USA, 10–15 June 2018; pp. 2357–2361. [Google Scholar]
- Khelifi, R.; Guermoui, M.; Rabehi, A.; Lalmi, D. Multi-step-ahead forecasting of daily solar radiation components in the Saharan climate. Int. J. Ambient Energy 2020, 41, 707–715. [Google Scholar] [CrossRef]
- Paulescu, M.; Paulescu, E. Short-term forecasting of solar irradiance. Renew. Energy 2019, 143, 985–994. [Google Scholar] [CrossRef]
- Vaz, A.; Elsinga, B.; Van Sark, W.; Brito, M. An artificial neural network to assess the impact of neighbouring photovoltaic systems in power forecasting in Utrecht, the Netherlands. Renew. Energy 2016, 85, 631–641. [Google Scholar] [CrossRef] [Green Version]
- Nobre, A.M.; Severiano, C.A., Jr.; Karthik, S.; Kubis, M.; Zhao, L.; Martins, F.R.; Pereira, E.B.; Rüther, R.; Reindl, T. PV power conversion and short-term forecasting in a tropical, densely-built environment in Singapore. Renew. Energy 2016, 94, 496–509. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Jieni, X.; Zhongke, S. Short-time traffic flow prediction based on chaos time series theory. J. Transp. Syst. Eng. Inf. Technol. 2008, 8, 68–72. [Google Scholar]
- Hand, D.J. Classifier technology and the illusion of progress. Stat. Sci. 2006, 21, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Kubat, M. Neural networks: A comprehensive foundation by Simon Haykin, Macmillan, 1994, ISBN 0-02-352781-7. Knowl. Eng. Rev. 1999, 13, 409–412. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Yang, J.; Kim, J. An accident diagnosis algorithm using long short-term memory. Nucl. Eng. Technol. 2018, 50, 582–588. [Google Scholar] [CrossRef]
- Gers, F.A.; Schraudolph, N.N.; Schmidhuber, J. Learning precise timing with LSTM recurrent networks. J. Mach. Learn. Res. 2002, 3, 115–143. [Google Scholar]
- Box, G.E.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, Revised Edition; Holden Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Al-Musaylh, M.S.; Deo, R.C.; Adamowski, J.F.; Li, Y. Short-term electricity demand forecasting using machine learning methods enriched with ground-based climate and ECMWF Reanalysis atmospheric predictors in southeast Queensland, Australia. Renew. Sustain. Energy Rev. 2019, 113, 109293. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Forecasting long-term global solar radiation with an ANN algorithm coupled with satellite-derived (MODIS) land surface temperature (LST) for regional locations in Queensland. Renew. Sustain. Energy Rev. 2017, 72, 828–848. [Google Scholar] [CrossRef]
- Fentis, A.; Bahatti, L.; Mestari, M.; Chouri, B. Short-term solar power forecasting using Support Vector Regression and feed-forward NN. In Proceedings of the 2017 15th IEEE International New Circuits and Systems Conference (NEWCAS), Strasbourg, France, 25–28 June 2017; pp. 405–408. [Google Scholar]
- Alfadda, A.; Adhikari, R.; Kuzlu, M.; Rahman, S. Hour-ahead solar PV power forecasting using SVR based approach. In Proceedings of the 2017 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 23–26 April 2017; pp. 1–5. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.J.; Vapnik, V. Support vector regression machines. In Proceedings of the Advances in Neural Information Processing Systems 9, Denver, CO, USA, 3–5 December 1996; pp. 155–161. [Google Scholar]
- Díaz–Vico, D.; Torres–Barrán, A.; Omari, A.; Dorronsoro, J.R. Deep neural networks for wind and solar energy prediction. Neural Process. Lett. 2017, 46, 829–844. [Google Scholar] [CrossRef]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Schmidt-Thomé, P.; Nguyen, T.H.; Pham, T.L.; Jarva, J.; Nuottimäki, K. Climate Change Adaptation Measures in Vietnam: Development and Implementation; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Nguyen, T.N.; Wongsurawat, W. Multivariate cointegration and causality between electricity consumption, economic growth, foreign direct investment and exports: Recent evidence from Vietnam. Int. J. Energy Econ. Policy 2017, 7, 287–293. [Google Scholar]
- Kies, A.; Schyska, B.; Viet, D.T.; von Bremen, L.; Heinemann, D.; Schramm, S. Large-scale integration of renewable power sources into the Vietnamese power system. Energy Procedia 2017, 125, 207–213. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Global solar radiation prediction by ANN integrated with European Centre for medium range weather forecast fields in solar rich cities of Queensland Australia. J. Clean. Prod. 2019, 216, 288–310. [Google Scholar] [CrossRef]
- Kotsiantis, S.; Kanellopoulos, D.; Pintelas, P. Data preprocessing for supervised leaning. Int. J. Comput. Sci. 2006, 1, 111–117. [Google Scholar]
- Keras-team, K.D. The Python Deep Learning Library. Available online: https://keras.io (accessed on 5 May 2019).
- Nawi, N.; Atomi, W.; Rehman, M. The effect of data pre-processing on optimized training of artificial neural networks. Procedia Technol. 2013, 11, 32–39. [Google Scholar] [CrossRef] [Green Version]
- Yu, R.; Gao, J.; Yu, M.; Lu, W.; Xu, T.; Zhao, M.; Zhang, J.; Zhang, R.; Zhang, Z. LSTM-EFG for wind power forecasting based on sequential correlation features. Future Gener. Comput. Syst. 2019, 93, 33–42. [Google Scholar] [CrossRef]
- Steyerberg, E.W.; Vickers, A.J.; Cook, N.R.; Gerds, T.; Gonen, M.; Obuchowski, N.; Pencina, M.J.; Kattan, M.W. Assessing the performance of prediction models: A framework for some traditional and novel measures. Epidemiology (Cambridge Mass.) 2010, 21, 128. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Nearing, G.S.; Peters-Lidard, C.D.; Harrison, K.W.; Tang, L. Performance metrics, error modeling, and uncertainty quantification. Mon. Weather Rev. 2016, 144, 607–613. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K.; Robeson, S.M. Ambiguities inherent in sums-of-squares-based error statistics. Atmos. Environ. 2009, 43, 749–752. [Google Scholar] [CrossRef]
- Willmott, C.J. On the evaluation of model performance in physical geography. In Spatial Statistics and Models; Springer: Dordrecht, The Netherlands, 1984; pp. 443–460. [Google Scholar]
- Wilcox, B.P.; Rawls, W.; Brakensiek, D.; Wight, J.R. Predicting runoff from rangeland catchments: A comparison of two models. Water Resour. Res. 1990, 26, 2401–2410. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Garrick, M.; Cunnane, C.; Nash, J. A criterion of efficiency for rainfall-runoff models. J. Hydrol. 1978, 36, 375–381. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- Ertekin, C.; Yaldiz, O. Comparison of some existing models for estimating global solar radiation for Antalya (Turkey). Energy Convers. Manag. 2000, 41, 311–330. [Google Scholar] [CrossRef]
- Tayman, J.; Swanson, D.A. On the validity of MAPE as a measure of population forecast accuracy. Popul. Res. Policy Rev. 1999, 18, 299–322. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Faber, N.K.M. Estimating the uncertainty in estimates of root mean square error of prediction: Application to determining the size of an adequate test set in multivariate calibration. Chemom. Intell. Lab. Syst. 1999, 49, 79–89. [Google Scholar] [CrossRef]
- Coyle, E.J.; Lin, J.-H. Stack filters and the mean absolute error criterion. IEEE Trans. Acoust. Speechand Signal Process. 1988, 36, 1244–1254. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 2002, 20, 134–144. [Google Scholar] [CrossRef]
- Chen, H.; Wan, Q.; Wang, Y. Refined Diebold-Mariano test methods for the evaluation of wind power forecasting models. Energies 2014, 7, 4185–4198. [Google Scholar] [CrossRef] [Green Version]
- Diebold, F.X. Comparing predictive accuracy, twenty years later: A personal perspective on the use and abuse of Diebold–Mariano tests. J. Bus. Econ. Stat. 2015, 33, 1. [Google Scholar] [CrossRef] [Green Version]
- Makridakis, S.; Wheelwright, S.C.; Hyndman, R.J. Forecasting Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Deo, R.C.; Wen, X.; Feng, Q. A wavelet-coupled support vector machine model for forecasting global incident solar radiation using limited meteorological dataset. Appl. Energy 2016, 168, 568–593. [Google Scholar] [CrossRef]








| Study | Data Source | Time Resolution | Forecast Horizon | The Number of Data Points | Method | ||
|---|---|---|---|---|---|---|---|
| Training Set | Testing Set | Proposed Method | Benchmark | ||||
| [78] | GSR | 5 min | 5 min | 24,260 | 8640 | BPNN | Fuzzy Logic-BPNN |
| [79] | GSR | 10 min | 10 min | 52,560 | 52,560 | ELM | Persistent, BELM |
| [80] | TSI | 1 min | 15 min | 68,833 | 8075 | CNN | N/A |
| [81] | GSR | 1 min | 10 min | N/A | N/A | MLP | RBF |
| [82] | TSI | 10 min | 20 min | 38,371 | 33,644 | ARIMA | RW, MA, ES |
| [83] | GSR | 15 min | 15 min | 21,170 | 1798 | ANN | ANN, MLP, NARX |
| [84] | GSR | 15 min | 15 min | 35,040 | 35,040 | ARIMA | Persistence |
| [46] | TSI, GSR | 1 min | 5, 10, 15, 20 min | 2016 | 864 | CNN | Persistence |
| [58] | GSR | 7.5 min | 7.5, 15, 30, 60 | 201, 480 | 67, 160 | LSTM | ARIMAX, MLP, Persistence |
| Forecasting Horizon | Data Period | Minimum Wm−2 | Maximum Wm−2 | Mean Wm−2 | Standard Deviation Wm−2 |
|---|---|---|---|---|---|
| 1 min (1 M) | 1 June 2019 to 30 June 2019 | 0 | 1376 | 207 | 283 |
| 5 min (5 M) | 1 March 2019 to 30 June 2019 | 0 | 6047 | 730 | 1157 |
| 10 min (10 M) | 27 September 2017 to 30 June 2019 | 0 | 11,889 | 1416 | 2297re |
| 15 min (15 M) | 27 September 2017 to 30 June 2019 | 0 | 16,574 | 2124 | 3430 |
| 30 min (30 M) | 27 September 2017 to 30 June 2019 | 0 | 32,042 | 4249 | 6804 |
| (a) | ||||||
| Forecast Horizon | Significant Lagged GSR | Number of Data Point | Training | Validation | Testing | |
| 80% | Percentage of Training Data | 20% | ||||
| 1 M | 18 | 43,197 | 34,558 | 10% | 8637 | |
| 5 M | 6 | 35,133 | 49,518 | 12,376 | ||
| 10 M | 3 | 92,874 | 24,757 | 6187 | ||
| 15 M | 19 | 61,897 | 34,558 | 8637 | ||
| 30 M | 10 | 30,946 | 28,106 | 7025 | ||
| (b) | ||||||
| Model | Training-Testing Proportion | r | RMSE (Wm−2) | MAE (Wm−2) | ||
| LSTM | 80–20 | 0.9957 | 32.086 | 13.670 | ||
| - | 70–30 | 0.9901 | 43.7088 | 15.715 | ||
| - | 60–40 | 0.9799 | 60.9179 | 23.402 | ||
| (a) | ||||||
| Model | Model Hyperparameters | Search Space for Optimal Hyperparameters | ||||
| LSTM | Hidden neurons | (100, 200, 300, 400, 500) | ||||
| - | Epochs | (1000, 1200, 1500, 2000) | ||||
| - | Optimizer | (Adam) | ||||
| - | Drop rate | (0.1, 0.2) | ||||
| - | Activation function | (ReLu) | ||||
| - | Layer 1 (L1) and Layer 2 (L2), Layer 3 (L3) | (50, 40, 40) | ||||
| - | Batch size | (400, 600, 700, 750, 800) | ||||
| (b) | ||||||
| Sequence | Initial Set-Up Epoch | Actual Used Epoch | Drop Rate | Batch Size | r | RMSE (Wm−2) |
| 1 | 2000 | 54 | 0.1 | 500 | 0.9874 | 33.201 |
| 2 | 2000 | 55 | 0.1 | 750 | 0.9875 | 33.178 |
| 3 | 2000 | 53 | 0.1 | 800 | 0.9884 | 33.098 |
| 4 | 2000 | 62 | 0.1 | 1000 | 0.9876 | 33.096 |
| 5 | 2000 | 64 | 0.2 | 800 | 0.9956 | 32.086 |
| (c) | ||||||
| Time-Horizon | GSR Model | Design Parameter | r | RMSE (Wm−2) | ||
| 1 M | LSTM | Number of epochs-Drop rate-Batch size | 64-0.1-800 | 0.9956 | 33.2012 | |
| DNN | Number of epochs-Drop rate-Batch size | 162-0.1-500 | 0.990 | 44.0424 | ||
| MLP | - | - | 0.9821 | 61.7642 | ||
| ARIMA | p-d-q | 0-1-0 | 0.9808 | 57.6876 | ||
| SVR | Cost Function (C), Epsilon (ε) | 1.0-1.0 | 0.9846 | 59.2223 | ||
| 5 M | LSTM | Number of epochs-Drop rate-Batch size | 59-0.2-800 | 0.9714 | 265.5456 | |
| DNN | Number of epochs-Drop rate-Batch size | 199-0.1-500 | 0.9650 | 1338.4922 | ||
| MLP | - | - | 0.9721 | 361.7641 | ||
| ARIMA | p-d-q | 0-1-0 | 0.9724 | 287.7479 | ||
| SVR | Cost Function (C), Epsilon (ε) | 1.0-1.0 | 0.9218 | 389.6317 | ||
| 10 M | LSTM | Number of epochs-Drop rate-Batch size | 59-0.2-800 | 0.9914 | 26.4411 | |
| DNN | Number of epochs-Drop rate-Batch size | 194-0.1-500 | 0.9871 | 26.6411 | ||
| MLP | - | - | 0.9599 | 26.3175 | ||
| ARIMA | p-d-q | 0-1-0 | 0.9205 | 22.622 | ||
| SVR | Cost Function (C), Epsilon (ε) | 1.0-1.0 | 0.9514 | 51.6976 | ||
| 15 M | LSTM | Number of epochs-Drop rate-Batch size | 70-0.2-500 | 0.9653 | 76.9883 | |
| DNN | Number of epochs-Drop rate-Batch size | 162-0.1-500 | 0.9657 | 88.9887 | ||
| MLP | - | - | 0.9547 | 220.7234 | ||
| ARIMA | p-d-q | 0-1-0 | 0.9618 | 1033.4372 | ||
| SVR | Cost Function (C), Epsilon (ε) | 0.8983 | 117.7362 | |||
| 30 M | LSTM | Number of epochs-Drop rate-Batch size | 62-0.2-500 | 0.9572 | 710.7477 | |
| DNN | Number of epochs-Drop rate-Batch size | 28-0.1-700 | 0.9067 | 709.0347 | ||
| MLP | - | - | 0.9192 | 900.1132 | ||
| ARIMA | p-d-q | 0-1-0 | 0.8859 | 952.8502 | ||
| SVR | Cost Function (C), Epsilon (ε) | 1.0-1.0 | 0.8314 | 1270.7158 | ||
| Predictive Model | r | RMSE | MAE | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 M | 5 M | 10 M | 15 M | 30 M | 1 M | 5 M | 10 M | 15 M | 30 M | 1 M | 5 M | 10 M | 15 M | 30 M | |
| LSTM | 0.9920 | 0.9999 | 0.9999 | 0.9578 | 0.9531 | 40.9125 | 1400 | 18.6627 | 79.7273 | 731.7482 | 21.6428 | 1059 | 12.3368 | 43.8383 | 409.7196 |
| MLP | 0.9780 | 0.9266 | 0.9062 | 0.9246 | 0.8554 | 65.7511 | 1852 | 88.9537 | 218.7543 | 1254.3440 | 34.2960 | 1326 | 53.8914 | 106.8205 | 778.1039 |
| DNN | 0.9910 | 0.9606 | 0.9998 | 0.9568 | 0.9094 | 44.4086 | 1570 | 61.8762 | 86.6580 | 940.4280 | 25.5140 | 1134 | 40.9027 | 49.0178 | 576.9220 |
| ARIMA | 0.9902 | 0.9607 | 0.9989 | 0.9584 | 0.9094 | 52.9785 | 1589 | 37.8037 | 161.1655 | 937.1356 | 31.9632 | 1149 | 24.9898 | 100.5221 | 571.3325 |
| SVR | 0.9856 | 0.9266 | 0.9358 | 0.9247 | 0.8555 | 56.1271 | 1619 | 74.8298 | 99.9360 | 1244.6963 | 31.5000 | 1136 | 42.1483 | 70.2232 | 773.6047 |
| Predictive Model | WI | RRMSE (%) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 M | 5 M | 10 M | 15 M | 30 M | 1 M | 5 M | 10 M | 15 M | 30 M | 1 M | 5 M | 10 M | 15 M | 30 M | |
| LSTM | 0.9984 | 0.9409 | 0.9989 | 0.9770 | 0.9811 | 0.9831 | 0.6420 | 0.9920 | 0.8712 | 0.8931 | 9.9278 | 51.7123 | 10.1362 | 42.1591 | 41.0858 |
| MLP | 0.9959 | 0.8816 | 0.9721 | 0.9167 | 0.9347 | 0.9563 | 0.3737 | 0.8188 | 0.0306 | 0.6859 | 15.9581 | 68.3986 | 48.3132 | 115.6755 | 70.4282 |
| DNN | 0.9981 | 0.9227 | 0.9844 | 0.9717 | 0.9718 | 0.9800 | 0.5500 | 0.9123 | 0.8479 | 0.8235 | 10.7782 | 57.9785 | 33.6067 | 45.8240 | 52.8026 |
| ARIMA | 0.9972 | 0.9202 | 0.9947 | 0.9500 | 0.9700 | 0.9716 | 0.5386 | 0.9673 | 0.4738 | 0.8247 | 12.8582 | 58.7073 | 20.5322 | 85.2231 | 52.6178 |
| SVR | 0.9969 | 0.9179 | 0.9801 | 0.9635 | 0.9364 | 0.9681 | 0.5212 | 0.8718 | 0.7977 | 0.6907 | 13.6223 | 59.8060 | 40.6421 | 52.8454 | 69.8865 |
| Predictive Model | LM | MAPE (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 M | 5 M | 10 M | 15 M | 30 M | 1 M | 5 M | 10 M | 15 M | 30 M | |
| LSTM | 0.9204 | 0.4658 | 0.9275 | 0.7575 | 0.7741 | 16 | 48 | 100 | 86 | 116 |
| MLP | 0.8739 | 0.3311 | 0.6832 | 0.4090 | 0.5710 | 47 | 54 | 127 | 143 | 49 |
| DNN | 0.9062 | 0.4279 | 0.7596 | 0.7288 | 0.6819 | 49 | 58 | 60 | 62 | 67 |
| ARIMA | 0.8825 | 0.4203 | 0.8531 | 0.4438 | 0.6850 | 233 | 267 | 151 | 127 | 85 |
| SVR | 0.8842 | 0.4272 | 0.7522 | 0.6115 | 0.5734 | 56 | 91 | 143 | 120 | 262 |
| Diebold–Mariano (DM) Test Statistics Forecast Horizon | LSTM vs. DNN | LSTM vs. ARIMA | LSTM vs. MLP | LSTM vs. SVR |
|---|---|---|---|---|
| 1 Min (1 M) | - | - | - | - |
| DM statistic | −0.272 | −24.381 | −25.824 | −16.933 |
| p-value | 0.785 | 0.000 | 0.000 | 0.000 |
| Reject Null Hypothesis | No | Yes | Yes | Yes |
| 5 Min (5 M) | - | - | - | - |
| DM statistic | 46.585 | 46.394 | −50.779 | 43.614 |
| p-value | 0.000 | 0.000 | 0.000 | 0.000 |
| Reject Null Hypothesis | Yes | Yes | Yes | Yes |
| 10 Min (10 M) | - | - | - | - |
| DM statistic | 62.231 | 27.318 | 62.231 | 32.816 |
| p-value | 0.000 | 0.000 | 0.000 | 0.000 |
| Reject Null Hypothesis | Yes | Yes | Yes | Yes |
| 15 Min (15 M) | - | - | - | - |
| DM statistic | −51.638 | −29.999 | 39.581 | −0.268 |
| p-value | 0.000 | 0.000 | 0.000 | 0.789 |
| Reject Null Hypothesis | Yes | Yes | Yes | No |
| Half Hourly (30 M) | - | - | - | - |
| DM statistic | −9.209 | 18.234 | −19.558 | 17.000 |
| p-value | 0.000 | 0.000 | 0.000 | 0.000 |
| Reject Null Hypothesis | Yes | Yes | Yes | Yes |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huynh, A.N.-L.; Deo, R.C.; An-Vo, D.-A.; Ali, M.; Raj, N.; Abdulla, S. Near Real-Time Global Solar Radiation Forecasting at Multiple Time-Step Horizons Using the Long Short-Term Memory Network. Energies 2020, 13, 3517. https://doi.org/10.3390/en13143517
Huynh AN-L, Deo RC, An-Vo D-A, Ali M, Raj N, Abdulla S. Near Real-Time Global Solar Radiation Forecasting at Multiple Time-Step Horizons Using the Long Short-Term Memory Network. Energies. 2020; 13(14):3517. https://doi.org/10.3390/en13143517
Chicago/Turabian StyleHuynh, Anh Ngoc-Lan, Ravinesh C. Deo, Duc-Anh An-Vo, Mumtaz Ali, Nawin Raj, and Shahab Abdulla. 2020. "Near Real-Time Global Solar Radiation Forecasting at Multiple Time-Step Horizons Using the Long Short-Term Memory Network" Energies 13, no. 14: 3517. https://doi.org/10.3390/en13143517
APA StyleHuynh, A. N. -L., Deo, R. C., An-Vo, D. -A., Ali, M., Raj, N., & Abdulla, S. (2020). Near Real-Time Global Solar Radiation Forecasting at Multiple Time-Step Horizons Using the Long Short-Term Memory Network. Energies, 13(14), 3517. https://doi.org/10.3390/en13143517