A Data-Driven Approach for Lithology Identification Based on Parameter-Optimized Ensemble Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Studied Data
2.2. Methods
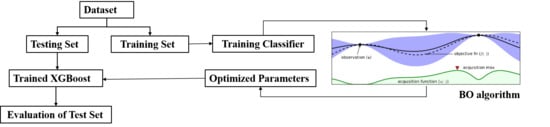
2.2.1. Extreme Gradient Boosting
2.2.2. Bayesian Optimization
- (1)
- Explore. Select unevaluated parameter combinations as much as possible to avoid local optimal values, so the posterior probability of will reach the true value of .
- (2)
- Exploit. Based on the optimal values found, after searching the parameters around, the global optimum can be found faster.
2.2.3. Details of Implementation
3. Performance Measure
4. Results and Discussion
4.1. Tuning Process
4.2. Evaluation Matrix
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| XGBoost | Extreme Gradient Boosting |
| BO | Bayesian Optimization |
| AUC | Rceiver operating characteristic curve |
| GTB-DE | Gradient Tree Boosting-Differential Evolution |
| PCA | Principal component analysis |
| ANN | Artificial neural networks |
| SVM | Support vector machine |
| RF | Random Forest |
| DGF | Daniudi gas field |
| HGF | Hangjinqi gas field |
| AC | Acoustic log |
| CAL | Caliper log |
| GR | Gamma ray log |
| LLD | Deep latero log |
| LLS | Shallow latero log |
| DEN | Density log |
| Q1 | The first quartiles |
| Q3 | The third quartiles |
| IQR | The interquartile range |
| LIF | Lower Inner Fence |
| UIF | Upper Inner Fence |
| CR | Carbonate rock |
| C | Coarse sandstone |
| PS | Pebbly sandstone |
| CS | Coarse sandstone |
| MS | Medium sandstone |
| FS | Fine sandstone |
| S | Siltstone |
| M | Mudstone |
| TP | True positive |
| FP | False positive |
| TN | True negative |
| FN | False negative |
| ROC | Receiver operating characteristics |
| TPR | True positive rate |
| FPR | False positive rate |
References
- Chen, G.; Chen, M.; Hong, G.; Lu, Y.; Zhou, B.; Gao, Y. A New Method of Lithology Classification Based on Convolutional Neural Network Algorithm by Utilizing Drilling String Vibration Data. Energies 2020, 13, 888. [Google Scholar] [CrossRef] [Green Version]
- Santos, S.M.G.; Gaspar, A.T.F.S.; Schiozer, D.J. Managing reservoir uncertainty in petroleum field development: Defining a flexible production strategy from a set of rigid candidate strategies. J. Pet. Sci. Eng. 2018, 171, 516–528. [Google Scholar] [CrossRef]
- Liu, H.; Wu, Y.; Cao, Y.; Lv, W.; Han, H.; Li, Z.; Chang, J. Well Logging Based Lithology Identification Model Establishment Under Data Drift: A Transfer Learning Method. Sensors 2020, 20, 3643. [Google Scholar] [CrossRef] [PubMed]
- Obiadi, I.I.; Okoye, F.C.; Obiadi, C.M.; Irumhe, P.E.; Omeokachie, A.I. 3-D structural and seismic attribute analysis for field reservoir development and prospect identification in Fabianski Field, onshore Niger delta, Nigeria. J. Afr. Earth Sci. 2019, 158, 12. [Google Scholar] [CrossRef]
- Saporetti, C.M.; da Fonseca, L.G.; Pereira, E.; de Oliveira, L.C. Machine learning approaches for petrographic classification of carbonate-siliciclastic rocks using well logs and textural information. J. Appl. Geophys. 2018, 155, 217–225. [Google Scholar] [CrossRef]
- Logging, C. Reservoir characteristics of oil sands and logging evaluation methods: A case study from Ganchaigou area, Qaidam Basin. Lithol. Reserv. 2015, 27, 119–124. [Google Scholar]
- Harris, J.R.; Grunsky, E.C. Predictive lithological mapping of Canada’s North using Random Forest classification applied to geophysical and geochemical data. Comput. Geosci. 2015, 80, 9–25. [Google Scholar] [CrossRef]
- Vasini, E.M.; Battistelli, A.; Berry, P.; Bonduà, S.; Bortolotti, V.; Cormio, C.; Pan, L. Interpretation of production tests in geothermal wells with T2Well-EWASG. Geothermics 2018, 73, 158–167. [Google Scholar] [CrossRef] [Green Version]
- Wood, D.A. Lithofacies and stratigraphy prediction methodology exploiting an optimized nearest-neighbour algorithm to mine well-log data. Mar. Pet. Geol. 2019, 110, 347–367. [Google Scholar] [CrossRef]
- Bressan, T.S.; Kehl de Souza, M.; Girelli, T.J.; Junior, F.C. Evaluation of machine learning methods for lithology classification using geophysical data. Comput. Geosci. 2020, 139, 104475. [Google Scholar] [CrossRef]
- Tewari, S.; Dwivedi, U.D. Ensemble-based big data analytics of lithofacies for automatic development of petroleum reservoirs. Comput. Ind. Eng. 2019, 128, 937–947. [Google Scholar] [CrossRef]
- Konaté, A.A.; Ma, H.; Pan, H.; Qin, Z.; Ahmed, H.A.; Dembele, N.d.d.J. Lithology and mineralogy recognition from geochemical logging tool data using multivariate statistical analysis. Appl. Radiat. Isotopes 2017, 128, 55–67. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Pan, H.; Ma, H.; Konaté, A.A.; Yao, J.; Guo, B. Performance of the synergetic wavelet transform and modified K-means clustering in lithology classification using nuclear log. J. Pet. Sci. Eng. 2016, 144, 1–9. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Carr, T.R.; Pal, M. Comparison of supervised and unsupervised approaches for mudstone lithofacies classification: Case studies from the Bakken and Mahantango-Marcellus Shale, USA. J. Nat. Gas. Sci. Eng. 2016, 33, 1119–1133. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.; Asante-Okyere, S.; Ziggah, Y.Y.; Wang, L.; Zhu, X. Group Method of Data Handling (GMDH) Lithology Identification Based on Wavelet Analysis and Dimensionality Reduction as Well Log Data Pre-Processing Techniques. Energies 2019, 12, 1509. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Hou, J.; Song, S.; Liu, Y.; Chen, D.; Wang, X.; Dou, L. Lithology identification using well logs: A method by integrating artificial neural networks and sedimentary patterns. J. Pet. Sci. Eng. 2019, 182, 106336. [Google Scholar] [CrossRef]
- Wang, G.; Carr, T.R.; Ju, Y.; Li, C. Identifying organic-rich Marcellus Shale lithofacies by support vector machine classifier in the Appalachian basin. Comput. Geosci. 2014, 64, 52–60. [Google Scholar] [CrossRef]
- Sun, J.; Li, Q.; Chen, M.; Ren, L.; Huang, G.; Li, C.; Zhang, Z. Optimization of models for a rapid identification of lithology while drilling-A win-win strategy based on machine learning. J. Pet. Sci. Eng. 2019, 176, 321–341. [Google Scholar] [CrossRef]
- Xie, Y.; Zhu, C.; Zhou, W.; Li, Z.; Liu, X.; Tu, M. Evaluation of machine learning methods for formation lithology identification: A comparison of tuning processes and model performances. J. Pet. Sci. Eng. 2018, 160, 182–193. [Google Scholar] [CrossRef]
- Torun, H.M.; Swaminathan, M.; Davis, A.K.; Bellaredj, M.L.F. A global Bayesian optimization algorithm and its application to integrated system design. IEEE Trans. Very Large Scale Integr. Syst. 2018, 26, 792–802. [Google Scholar] [CrossRef]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452–459. [Google Scholar] [CrossRef] [PubMed]
- Tukey, J.W. Mathematics and the picturing of data. In Proceedings of the International Congress of Mathematicians, Vancouver, BC, USA, 1975; pp. 523–531. [Google Scholar]
- Zhu, X. Sedimentary Petrology; Petroleum Industry Press: Beijing, China, 2008. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Zhang, L.; Zhan, C. Machine Learning in Rock Facies Classification: An Application of XGBoost. In Proceedings of the International Geophysical Conference, Qingdao, China, 17–20 April 2017; Society of Exploration Geophysicists and Chinese Petroleum Society: Beijing, China, 2017; pp. 1371–1374. [Google Scholar]
- Wang, Z.; Hutter, F.; Zoghi, M.; Matheson, D.; de Feitas, N. Bayesian optimization in a billion dimensions via random embeddings. J. Artif. Intell. Res. 2016, 55, 361–387. [Google Scholar]
- Wang, J.; Hertzmann, A.; Fleet, D.J. Gaussian process dynamical models. In Advances in Neural Information Processing Systems; A Bradford Book: Cambridge, MA, USA, 2006; pp. 1441–1448. [Google Scholar]
- Muhuri, P.K.; Biswas, S.K. Bayesian optimization algorithm for multi-objective scheduling of time and precedence constrained tasks in heterogeneous multiprocessor systems. Appl. Soft Comput. 2020, 92, 106274. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Babchishin, K.M.; Helmus, L.M. The influence of base rates on correlations: An evaluation of proposed alternative effect sizes with real-world data. Behav. Res. Methods 2016, 48, 1021–1031. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saporetti, C.M.; da Fonseca, L.G.; Pereira, E. A Lithology Identification Approach Based on Machine Learning with Evolutionary Parameter Tuning. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1819–1823. [Google Scholar] [CrossRef]








| Parameter | Mean | Min | Q1 | Median | Q3 | Max | IQR |
|---|---|---|---|---|---|---|---|
| AC (μs/m) | 238.99 | 159 | 214.04 | 232.3 | 251.92 | 608.6 | 56.82 |
| CAL (cm) | 25.04 | 21.39 | 22.85 | 24.28 | 26.28 | 44.78 | 5.14 |
| GR (API) | 93.03 | 24.27 | 63.58 | 83.71 | 118.93 | 771.34 | 83.03 |
| LLD (Ωm) | 931.53 | 5.35 | 14.50 | 31.85 | 73.59 | 99,990.00 | 88.64 |
| LLS (Ωm) | 291.73 | 5.54 | 15.28 | 32.56 | 71.43 | 26,057.18 | 84.23 |
| DEN (g/cm3) | 2.46 | 1.21 | 2.42 | 2.53 | 2.601 | 2.97 | 0.27 |
| CNL (%) | 21.48 | 0.4 | 14.24 | 17.96 | 26.27 | 92.77 | 18.05 |
| Tuned Parameters | Search Range | Optimum Value in the DGF | Optimum Value in the HGF |
|---|---|---|---|
| Number of estimators | 10–1000 | 978 | 18 |
| Max depth | 1–20 | 18 | 10 |
| Learning rate | 1 × 10−3–5 × −1 | 0.08 | 0.14 |
| Subsample | 0.1–1 | 0.93 | 0.77 |
| Min child weight | 1–10 | 3.9 | 1 |
| Gamma | 0.1–0.6 | 0.35 | 0.11 |
| Colsample bytree | 0.5–1 | 0.51 | 0.52 |
| Reg alpha | 1 × 10−5–1 × 10−2 | 0.003 | 0.008 |
| Class | Precision | Recall | F1 Score |
|---|---|---|---|
| PS | 0.802 | 0.789 | 0.800 |
| CS | 0.603 | 0.648 | 0.622 |
| FS | 0.985 | 0.737 | 0.843 |
| M | 0.799 | 0.923 | 0.854 |
| MS | 0.711 | 0.809 | 0.760 |
| C | 0.999 | 0.935 | 0.961 |
| S | 0.992 | 0.928 | 0.954 |
| CR | 1 | 0.920 | 0.955 |
| avg | 0.861 | 0.836 | 0.843 |
| Class | Precision | Recall | F1 Score |
|---|---|---|---|
| PS | 0.862 | 0.919 | 0.889 |
| CS | 0.893 | 0.900 | 0.887 |
| FS | 0.894 | 0.875 | 0.897 |
| M | 0.936 | 0.932 | 0.934 |
| MS | 0.909 | 0.867 | 0.888 |
| C | 0.982 | 0.979 | 0.969 |
| S | 0.976 | 0.816 | 0.888 |
| avg | 0.922 | 0.898 | 0.908 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Jiang, B.; Li, X.; Li, J.; Xiao, K. A Data-Driven Approach for Lithology Identification Based on Parameter-Optimized Ensemble Learning. Energies 2020, 13, 3903. https://doi.org/10.3390/en13153903
Sun Z, Jiang B, Li X, Li J, Xiao K. A Data-Driven Approach for Lithology Identification Based on Parameter-Optimized Ensemble Learning. Energies. 2020; 13(15):3903. https://doi.org/10.3390/en13153903
Chicago/Turabian StyleSun, Zhixue, Baosheng Jiang, Xiangling Li, Jikang Li, and Kang Xiao. 2020. "A Data-Driven Approach for Lithology Identification Based on Parameter-Optimized Ensemble Learning" Energies 13, no. 15: 3903. https://doi.org/10.3390/en13153903
APA StyleSun, Z., Jiang, B., Li, X., Li, J., & Xiao, K. (2020). A Data-Driven Approach for Lithology Identification Based on Parameter-Optimized Ensemble Learning. Energies, 13(15), 3903. https://doi.org/10.3390/en13153903