Application of the 2-D Trefftz Method for Identification of Flow Boiling Heat Transfer Coefficient in a Rectangular MiniChannel
Abstract
:1. Introduction
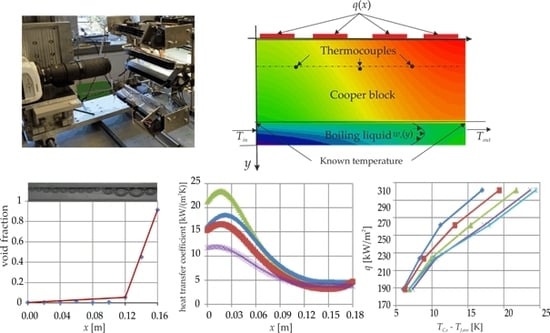
2. Experimental Facility
2.1. Design of the Flow Loop, Experimental Equipment and Data Collecting Procedure
2.2. Procedure of Void Fraction Measurement and Computation in Rectangular Minichannel
- Small vapor bubbles: Rsb, i ≤ b/2.
- 2.
- Large, elongated bubbles, fully visible: ellipse semi-axes P1 lb, i= a/2 and P2 lb, i= b/2.
- 3.
- Large, elongated bubbles, partially visible: ellipse semi-axes P1 lb, i= a/2 and P2 lb, i= b/2.
3. Mathematical Model and Numeric Solution
- -
- The flow in the horizontal minichannel was laminar (Re < 2000) and stationary with a constant volumetric flow rate,
- -
- Liquid flow in the minichannel was a nonslip flow and the velocity of the fluid had only one non-zero parabolic component wx(y), parallel to the heating block and satisfying the condition:where the wave was known
- -
- The fluid temperatures at the inlet Tf, in and outlet Tf, out of the minichannel were known,
- -
- The fluid temperature at the contact with the heater block fulfilled the condition:
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Nomenclature | |
| A | area, cross-section, m2 |
| a | channel width, m |
| b | channel depth, m |
| cp | specific heat, J/(kgK) |
| D | domain, mm |
| f | Fanning friction factor |
| G | mass flux, kg/(m2 s) |
| H | height, m |
| L | length, m |
| MRE | mean relative error |
| p | pressure, Pa |
| P | ellipse semi-axis, m |
| Pr | Prandtl number |
| q | heat flux, kW/m2 |
| R | radius, m |
| Re | Reynolds number |
| T | temperature, K, °C |
| w | velocity, m/s |
| x | coordinate in the flow direction, m |
| y | coordinate perpendicular to the flow direction, m |
| V | volume, m3 |
| Laplacian in Cartesian coordinates | |
| Greek symbol | |
| α | heat transfer coefficient, W/(m2 K) |
| Δ | difference |
| Φ | Rayleigh dissipation function, s-2 |
| ϕ | void fraction |
| λ | thermal conductivity, W/(m K) |
| μ | dynamic viscosity, Pa s |
| ρ | density, kg/m3 |
| Ω | negative heat source, W/m3 |
| Subscripts | |
| approx | approximation |
| ave | average |
| b | bubble |
| C | copper block |
| cam | observed part of the minichannel |
| con | convection |
| f | fluid |
| h | hydraulic |
| i | i–th bubble, |
| in | inlet |
| lb | large bubble |
| out | outlet |
| s | surface |
| sat | saturation |
| sb | small bubble |
| T | thermal |
| X | in the flow direction |
References
- Kim, S.-M.; Mudawar, I. Review of databases and predictive methods for heat transfer in condensing and boiling mini/micro-channel flows. Int. J. Heat Mass Transf. 2014, 77, 627–652. [Google Scholar] [CrossRef]
- Grabowski, M.; Hożejowska, S.; Poniewski, M.E. Trefftz method-based identification of heat transfer coefficient and temperature fields in flow boiling in an asymmetrically heated rectangular mini-channel. In Proceedings of the XV Symposium on Heat and Mass Transfer 2019 (SOHAMT 2019), Kołobrzeg, Poland, 16–19 September 2019; Volume 1, pp. 179–192. [Google Scholar]
- Karayiannis, T.G.; Mahmoud, M.M. Flow boiling in microchannels: Fundamentals and applications. Appl. Therm. Eng. 2017, 115, 1372–1397. [Google Scholar] [CrossRef]
- Płaczkowski, K.; Poniewski, M.E.; Grabowski, M.; Alabrudziinski, S. Photographic technique application to the determination of void fraction in two-phase flow boiling in minichannels. Appl. Mech. Mater. 2015, 797, 299–306. [Google Scholar] [CrossRef]
- Saisorn, S.; Kaew-On, J.; Wongwises, S. Flow pattern and heat transfer characteristics of R-134a refrigerant during flow boiling in a horizontal circular mini-channel. Int. J. Heat Mass Transf. 2010, 53, 4023–4038. [Google Scholar] [CrossRef]
- Trefftz, E. Ein Gegenstück zum Ritzschen Verfahren. In Proceedings of the International Kongress für Technische Mechanik, Zürich, Switzerland, 12–17 September 1926; pp. 131–137. [Google Scholar]
- Piasecka, M.; Hożejowska, S.; Poniewski, M.E. Experimental evaluation of flow boiling incipience of subcooled fluid in a narrow channel. Int. J. Heat Fluid Flow 2004, 25, 159–172. [Google Scholar] [CrossRef]
- Hożejowska, S.; Piasecka, M.; Poniewski, M.E. Boiling heat transfer in vertical minichannels. Liquid crystal experiments and numerical investigations. Int. J. Therm. Sci. 2009, 48, 1049–1059. [Google Scholar] [CrossRef]
- Hożejowska, S.; Kaniowski, R.; Poniewski, M.E. Trefftz method for calculating temperature field of the boiling liquid flowing in a minichannel. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 811–824. [Google Scholar] [CrossRef]
- Grabowski, M.; Hożejowska, S.; Pawinska, A.; Poniewski, M.E.; Wernik, J. Heat Transfer Coefficient Identification in Mini-Channel Flow Boiling with the Hybrid Picard-Trefftz Method. Energies 2018, 11, 2057. [Google Scholar] [CrossRef] [Green Version]
- Fan, C.-M.; Chan, H.-F.; Kuo, C.-L.; Yeih, W. Numerical solutions of boundary detection problems using modified collocation Trefftz method and exponentially convergent scalar homotopy algorithm. Eng. Anal. Bound. Elem. 2012, 36, 2–8. [Google Scholar] [CrossRef]
- Płaczkowski, K. Application of Photographic Technology to the Two-Phase Flow Regime Recording and Concurrent Void Fraction Quantification (In Polish). Ph.D. Thesis, Warsaw University of Technology, Płock, Poland, 2020. [Google Scholar]
- Hożejowska, S.; Grabowski, M.; Poniewski, M.E. Implementation of a three-dimensional model for the identification of flow boiling heat transfer coefficient in rectangular mini-channel. In Proceedings of the International Conference on Experimental Fluid Mechanics, Franzensbad, Czech Republic, 19–22 November 2019; Dančová, P., Ed.; Technical University of Liberec and MiTpp: Liberec, Czech Republic, 2001; pp. 178–182. [Google Scholar]
- Bilicki, Z. Latent heat transport in forced boiling flow. Int. J. Heat Mass Transf. 1983, 26, 559–565. [Google Scholar] [CrossRef]
- Bilicki, Z. The relation between the experiment and theory for nucleate forced boiling, Invited lecture. In Proceedings of the 4th ExHFT, Brussels, Belgium, 2–6 June 1997; pp. 571–578. [Google Scholar]
- Bohdal, T. Modeling the process of bubble boiling on flows. Arch. Thermodyn. 2000, 21, 34–75. [Google Scholar]
- Tolubinski, V.I.; Kostanchuk, D.M. Vapour bubbles growth rate and heat transfer intensity at subcooled water boiling. In Proceedings of the 4th International Heat Transfer Conference, Paris-Versailles, France, 31 August–5 September 1970; pp. 1–11. [Google Scholar]
- Labuncov, D.A. Obobščennyie zavisimosti dla teplootdači pri puzirkovom kipenii židkosti. Teploenergetika 1960, 5, 76–81. [Google Scholar]
- Shah, R.K.; London, A.L. Laminar Flow Forced Convection in Ducts; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Hożejowski, L.; Hożejowska, S. Trefftz method in an inverse problem of two-phase flow boiling in a minichannel. Eng. Anal. Bound. Elem. 2019, 98, 27–34. [Google Scholar] [CrossRef]
- Layssac, T.; Lips, S.; Revellin, R. Effect of inclination on heat transfer coefficient during flow boiling in a mini-channel. Int. J. Heat Mass Transf. 2019, 132, 508–518. [Google Scholar] [CrossRef]















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grabowski, M.; Hożejowska, S.; Maciejewska, B.; Płaczkowski, K.; Poniewski, M.E. Application of the 2-D Trefftz Method for Identification of Flow Boiling Heat Transfer Coefficient in a Rectangular MiniChannel. Energies 2020, 13, 3973. https://doi.org/10.3390/en13153973
Grabowski M, Hożejowska S, Maciejewska B, Płaczkowski K, Poniewski ME. Application of the 2-D Trefftz Method for Identification of Flow Boiling Heat Transfer Coefficient in a Rectangular MiniChannel. Energies. 2020; 13(15):3973. https://doi.org/10.3390/en13153973
Chicago/Turabian StyleGrabowski, Mirosław, Sylwia Hożejowska, Beata Maciejewska, Krzysztof Płaczkowski, and Mieczysław E. Poniewski. 2020. "Application of the 2-D Trefftz Method for Identification of Flow Boiling Heat Transfer Coefficient in a Rectangular MiniChannel" Energies 13, no. 15: 3973. https://doi.org/10.3390/en13153973
APA StyleGrabowski, M., Hożejowska, S., Maciejewska, B., Płaczkowski, K., & Poniewski, M. E. (2020). Application of the 2-D Trefftz Method for Identification of Flow Boiling Heat Transfer Coefficient in a Rectangular MiniChannel. Energies, 13(15), 3973. https://doi.org/10.3390/en13153973