Battery Models for Battery Powered Applications: A Comparative Study
Abstract
:1. Introduction
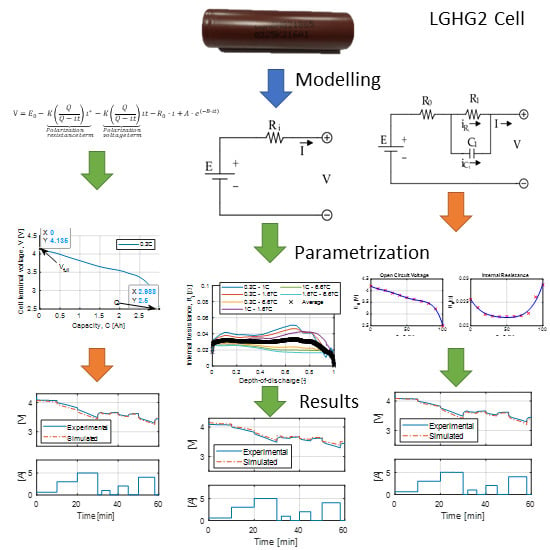
2. Battery Modeling and Parametrization
2.1. Shepherd Model
- represents the open circuit voltage of a battery at full capacity (V);
- is the polarization resistance coefficient ;
- is the battery capacity ;
- is the battery current ;
- is the internal resistance ;
- is the removed charge ;
- are empirical constants (V), (1/Ah).
- fully charged voltage , first point of the characteristic;
- end of the exponential zone ;
- end of the nominal zone (when the voltage starts to decrease quickly);
- maximum capacity , last point of the characteristic.
- ;
- ;
- ;
- ;
2.2. Rint Model
- is the Peukert Capacity (Ah);
- is the Peukert coefficient (-);
- is the discharge current (A);
- is the discharge time for discharge current (h).
2.3. Thevenin Model
3. Test-Bench Description
- a LG18650HG2 cell, whose characteristics are reported in Table 5;
- a Fluke PM2812 Programmable Power Supply, whose characteristics are reported in Table 6, used to charge the cells;
- an Agilent 6060B Single Input Electronic Load, whose characteristics are reported in Table 7, used on the discharge phase of the cell;
- a NI 9215 16-Bit Data Acquisition Board (placed in a NI cDAQ 9172 chassis), whose characteristics are reported in Table 8, used to acquire the cell voltage signal;
- a SRD05VDCSl-C 4-Channels Optical Isolated Relay;
- a NI 9401 Digital Module (placed in the NI cDAQ 9172 chassis), used to control the relay.
Measurement Uncertainty Evaluation
- considering a recutangular distribution for the offset error;
- considering a rectangular distribution for the gain error and considering the worst case that corresponds to the maximum measured value (4.2 V);
- considering a gaussian distribution for the noise and considering that each measured values is the mean of 1000 acquired samples.
- considering a rectangular distribution for the offset error;
- considering a rectangular distribution for the gain error and considering the worst case that corresponds to the maximum measured value (5 A);
- the noise error is expressed as rms value.
4. Validation of Models
- is the actual value at the considered instant ;
- is the simulated value at the considered instant ;
- is the maximum observed value.
- is the experimental value at the considered instant ;
- is the simulated vale at the considered instant ;
- is the number of samples of the experimental and simulated data.
4.1. Datasheet Discharge Curves
4.1.1. Shepherd Model Validation
4.1.2. Rint Model Validation
4.1.3. Thevenin Model Validation
4.2. Battery CC/CV Charge
4.3. Battery Pulse Discharge
4.4. Battery Dynamic Discharge
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Saldaña, G.; San Martín, J.I.; Zamora, I.; Asensio, F.J.; Oñederra, O. Analysis of the Current Electric Battery Models for Electric Vehicle Simulation. Energies 2019, 12, 2750. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Qin, H.; Sun, X.; Shui, Y. Comparison Study on the Battery SoC Estimation with EKF and UKF Algorithms. Energies 2013, 6, 5088. [Google Scholar] [CrossRef]
- Wang, D.; Bao, Y.; Shi, J. Online Lithium-Ion Battery Internal Resistance Measurement Application in State-of-Charge Estimation Using the Extended Kalman Filter. Energies 2017, 10, 1284. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Qiu, Y.; Guo, X. Prediction of State-of-Health for Nickel-Metal Hydride Batteries by a Curve Model Based on Charge-Discharge Tests. Energies 2015, 8, 2322. [Google Scholar] [CrossRef] [Green Version]
- Gismero, A.; Schaltz, E.; Stroe, D.-I. Recursive State of Charge and State of Health Estimation Method for Lithium-Ion Batteries Based on Coulomb Counting and Open Circuit Voltage. Energies 2020, 13, 1811. [Google Scholar] [CrossRef] [Green Version]
- Samadani, S.E.; Fraser, R.A.; Fowler, M. A Review Study of Methods for Lithium-ion Battery Health Monitoring and Remaining Life Estimation in Hybrid Electric Vehicles. SAE Tech. Paper Ser. 2012. [Google Scholar] [CrossRef]
- Raszmann, E.; Baker, K.; Shi, Y.; Christensen, D. Modeling stationary lithium-ion batteries for optimization and predictive control. In Proceedings of the 2017 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 23–24 February 2017; pp. 1–7. [Google Scholar]
- Jongerden, M.R.; Haverkort, B.R.H.M. Battery Modeling; Design and Analysis of Communication Systems (DACS): Enschede, The Netherlands, 2008. [Google Scholar]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modelling: From Lithium-ion toward Lithium–Sulphur. Renew. Sustain. Energy Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef] [Green Version]
- Barcellona, S.; Piegari, L. Lithium Ion Battery Models and Parameter Identification Techniques. Energies 2017, 10, 2007. [Google Scholar] [CrossRef] [Green Version]
- Damiano, A.; Porru, M.; Salimbeni, A.; Serpi, A.; Castiglia, V.; Di Tommaso, A.O.; Miceli, R.; Schettino, G. Batteries for Aerospace: A Brief Review. In Proceedings of the 2018 AEIT International Annual Conference, Bari, Italy, 3–5 October 2018; pp. 1–6. [Google Scholar]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and Optimization of the Dual Lithium Ion Insertion Cell. J. Electrochem. Soc. 1994, 141, 1. [Google Scholar] [CrossRef] [Green Version]
- Newman, J.; Tiedemann, W. Porous-electrode theory with battery applications. AIChE J. 1975, 21, 25–41. [Google Scholar] [CrossRef] [Green Version]
- Smith, K.; Wang, C.-Y. Solid-state diffusion limitations on pulse operation of a lithium ion cell for hybrid electric vehicles. J. Power Sources 2006, 161, 628–639. [Google Scholar] [CrossRef]
- Ahmed, R.; Sayed, M.E.; Arasaratnam, I.; Tjong, J.; Habibi, S. Reduced-Order Electrochemical Model Parameters Identification and SOC Estimation for Healthy and Aged Li-Ion Batteries Part I: Parameterization Model Development for Healthy Batteries. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 659–677. [Google Scholar] [CrossRef]
- Ahmed, R.; Sayed, M.E.; Arasaratnam, I.; Tjong, J.; Habibi, S. Reduced-Order Electrochemical Model Parameters Identification and State of Charge Estimation for Healthy and Aged Li-Ion Batteries—Part II: Aged Battery Model and State of Charge Estimation. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 678–690. [Google Scholar] [CrossRef]
- Fan, G.; Li, X.; Canova, M. A Reduced-Order Electrochemical Model of Li-Ion Batteries for Control and Estimation Applications. IEEE Trans. Veh. Technol. 2018, 67, 76–91. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J. The use of mathematical modeling in the design of lithium/polymer battery systems. Electrochim. Acta 1995, 40, 2191–2196. [Google Scholar] [CrossRef]
- Li, R.; Wang, Z.; Yu, J.; Lei, Y.; Zhang, Y.; He, J. Dynamic Parameter Identification of Mathematical Model of Lithium-Ion Battery Based on Least Square Method. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–5. [Google Scholar]
- Haoran, L.; Liangdong, L.; Xiaoyin, Z.; Mingxuan, S. Lithium Battery SOC Estimation Based on Extended Kalman Filtering Algorithm. In Proceedings of the 2018 IEEE 4th International Conference on Control Science and Systems Engineering (ICCSSE), Wuhan, China, 21–23 August 2018; pp. 231–235. [Google Scholar]
- Li, S.; Ke, B. Study of battery modeling using mathematical and circuit oriented approaches. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- Hinz, H. Comparison of Lithium-Ion Battery Models for Simulating Storage Systems in Distributed Power Generation. Inventions 2019, 4, 41. [Google Scholar] [CrossRef] [Green Version]
- Nikolian, A.; Firouz, Y.; Gopalakrishnan, R.; Timmermans, J.-M.; Omar, N.; Van den Bossche, P.; Van Mierlo, J. Lithium Ion Batteries—Development of Advanced Electrical Equivalent Circuit Models for Nickel Manganese Cobalt Lithium-Ion. Energies 2016, 9, 360. [Google Scholar] [CrossRef]
- Grandjean, T.R.B.; McGordon, A.; Jennings, P.A. Structural Identifiability of Equivalent Circuit Models for Li-Ion Batteries. Energies 2017, 10, 90. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Barreras, J.V.; Schaltz, E.; Andreasen, S.J.; Minko, T. Datasheet-based modeling of Li-Ion batteries. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, Korea, 9–12 October 2012; pp. 830–835. [Google Scholar]
- Castiglia, V.; Livreri, P.; Miceli, R.; Pellitteri, F.; Schettino, G.; Viola, F. Power Management of a Battery/Supercapacitor System for E-Mobility Applications. In Proceedings of the 2019 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Torino, Italy, 2–4 July 2019; pp. 1–5. [Google Scholar]
- Potrykus, S.; Kutt, F.; Nieznański, J.; Fernández Morales, F.J. Advanced Lithium-Ion Battery Model for Power System Performance Analysis. Energies 2020, 13, 2411. [Google Scholar] [CrossRef]
- Shepherd, C.M. Design of Primary and Secondary Cells: II. An Equation Describing Battery Discharge. J. Electrochem. Soc. 1965, 112, 657. [Google Scholar] [CrossRef]
- Enache, B.; Lefter, E.; Stoica, C. Comparative study for generic battery models used for electric vehicles. In Proceedings of the 2013 8th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 23–25 May 2013; pp. 1–6. [Google Scholar]
- Tremblay, O.; Dessaint, L.-A. Experimental Validation of a Battery Dynamic Model for EV Applications. World Electr. Veh. J. 2009, 3, 289. [Google Scholar] [CrossRef] [Green Version]
- Castiglia, V.; Miceli, R.; Ala, G.; Romano, P.; Viola, F.; Giglia, G.; Imburgia, A.; Schettino, G. Modelling, simulation and characterization of Li-Ion battery cell. In Proceedings of the 2019 IEEE 5th International Forum on Research and Technology for Society and Industry (RTSI), Florence, Italy, 9–12 September 2019; pp. 400–405. [Google Scholar]
- Doerffel, D.; Sharkh, S.A. A critical review of using the Peukert equation for determining the remaining capacity of lead-acid and lithium-ion batteries. J. Power Sources 2006, 155, 395–400. [Google Scholar] [CrossRef]
- Omar, N.; Bossche, P.V.d.; Coosemans, T.; Mierlo, J.V. Peukert Revisited—Critical Appraisal and Need for Modification for Lithium-Ion Batteries. Energies 2013, 6, 5625. [Google Scholar] [CrossRef]
- Plett, G.L. Modeling, Simulation, and Identification of Battery Dynamics. Available online: http://mocha-java.uccs.edu/ECE5710/index.html (accessed on 10 February 2020).
- JCGM 100. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. 2008. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 10 February 2020).


























[V] | Q [Ah] | [V] | [Ah] | [V] | [Ah] | |
|---|---|---|---|---|---|---|
| 4.135 | 2.998 | 3.301 | 2.592 | 3.123 | 2.761 | 0.025 |
[V] | K | A [V] | B [Ah] |
|---|---|---|---|
| 3.488 | 0.0085 | 0.6612 | 0.7716 |
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | Peukert Capacity | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4.18 | 4.08 | 3.98 | 3.88 | 3.78 | 3.69 | 3.63 | 3.57 | 3.46 | 3.24 | 2.5 | [Ah] | 2.97 | |
| 17.3 | 32.0 | 31.0 | 30.7 | 30.1 | 30.2 | 32.0 | 32.8 | 30.4 | 22.4 | 17.1 | k [-] | 1.02 | |
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4.20 | 4.08 | 4.01 | 3.89 | 3.80 | 3.70 | 3.63 | 3.55 | 3.46 | 3.22 | 2.5 | |
| 25.6 | 23.9 | 22.4 | 22.0 | 21.9 | 21.9 | 22.0 | 22.1 | 22.7 | 26.2 | 28.7 | |
| 16.9 | 20.0 | 25.2 | 22.3 | 22.1 | 25.0 | 30.0 | 25.7 | 29.9 | 43.3 | 56.7 | |
| 2.05 | 2.00 | 1.59 | 1.79 | 1.81 | 1.60 | 1.31 | 1.55 | 1.33 | 0.92 | 0.51 |
| Nominal Voltage | 3.7 V | Standard Charge Current | 1.5 A |
| Nominal capacity | 3000 mAh | Fast charge current | 4 A |
| Continuous discharge current | 20 A | Max voltage | 4.2 V |
| Initial internal resistance | 24–26 mΩ |
| Output Voltage Range | 0 to 60 V |
| Output current range | 0 to 5 A |
| Readback current accuracy | ± (0.1% + 15 mA) |
| Current noise | 10 mA |
| Input Voltage Range | 0 to 60 V |
| Input current range | 0 to 60 A |
| Maximum power | 300 W |
| Readback current accuracy | ± (0.05% + 65 mA) |
| Current noise | 4 mA rms |
| Signal Level | ± 10 V |
| Type of ADC | 16-Bit Successive Approximation |
| Channels | 4 Differential (simultaneously acquired) |
| Sample rate | 100 kS/s/ch |
| Accuracy (after calibration) | ± (0.02% + 1.5 mV) |
| Noise (peak-to-peak) | 2.2 mV |
| Model | Datasheet | Experimental Test | |||||
|---|---|---|---|---|---|---|---|
| 0.2 C | 1 C | 1.67 C | 6.67 C | CC/CV | PDT | DDT | |
| Shepherd | 24.9 | 25.8 | 47.8 | 298.4 | 137.6 | 65.2 | 49.2 |
| Rint | 12.9 | 43.5 | 46.5 | 90.2 | 141.6 | 36.2 | 49.9 |
| Thevenin | 18.1 | 33.0 | 0.3 | 208.9 | 69.1 | 14.8 | 43.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campagna, N.; Castiglia, V.; Miceli, R.; Mastromauro, R.A.; Spataro, C.; Trapanese, M.; Viola, F. Battery Models for Battery Powered Applications: A Comparative Study. Energies 2020, 13, 4085. https://doi.org/10.3390/en13164085
Campagna N, Castiglia V, Miceli R, Mastromauro RA, Spataro C, Trapanese M, Viola F. Battery Models for Battery Powered Applications: A Comparative Study. Energies. 2020; 13(16):4085. https://doi.org/10.3390/en13164085
Chicago/Turabian StyleCampagna, Nicola, Vincenzo Castiglia, Rosario Miceli, Rosa Anna Mastromauro, Ciro Spataro, Marco Trapanese, and Fabio Viola. 2020. "Battery Models for Battery Powered Applications: A Comparative Study" Energies 13, no. 16: 4085. https://doi.org/10.3390/en13164085
APA StyleCampagna, N., Castiglia, V., Miceli, R., Mastromauro, R. A., Spataro, C., Trapanese, M., & Viola, F. (2020). Battery Models for Battery Powered Applications: A Comparative Study. Energies, 13(16), 4085. https://doi.org/10.3390/en13164085