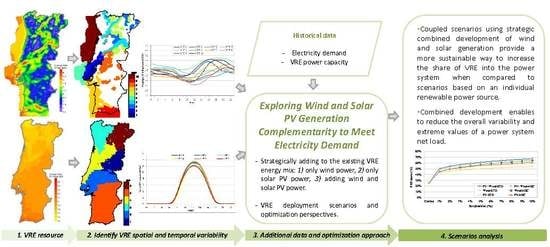
Exploring Wind and Solar PV Generation Complementarity to Meet Electricity Demand
Abstract
:1. Introduction
2. Holistic Renewable and Complementarity Assessment Methodology
2.1. Identification of Power Generation Patterns
2.2. Optimization Greedy Algorithm
3. Case Study and Data
3.1. Characteristics of the Portuguese Power System and Weather Conditions
3.2. Data
4. Identification and Characterization of the Spatial Power Patterns
4.1. Wind Power
4.2. Solar PV Power
5. Scenarios Identification and Renewables Deployment Results
5.1. Scenarios and Optimization Perspectives
5.2. Additional VRE Deployment Capacity and Daily Profiles
5.3. Net Load Duration Curve and Extreme Values
5.4. VRE Share Values in the Final Consumption
6. Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Glossary
| Cluster medoid of the K-th cluster | PV + WindHSC | Scenario using only wind and solar PV technologies and the HSC objective function | |
| CH | Calinski-Harabasz | RES | Renewable energy sources |
| CMSAF | Satellite Application Facility on Climate Monitoring | s | Number of solar PV regions identified using the cluster approach |
| D | Distance between the observations and the medoid of each cluster | Area need to install a 10 MW solar PV park | |
| HSC | Scenarios using the hourly NL step change standard deviation minimization | Existing national aggregated solar PV hourly generation | |
| i | Spatial points of the 5 × 5 km resolution available | Area available for additional solar PV power capacity deployment for the s-th region | |
| it | Number of installations units | SPP | Solar PV production patterns |
| K | Number of clusters | STD | Scenarios using the minimize NL annual variability objective function |
| Percentage of maximum area available in each region. | Percentage allowed VRE energy generation regarding the annual electricity consumption | ||
| MM5 | Fifth-generation mesoscale model | t | Index domain for time |
| n | Number of records available | TSO | Transmission system operator |
| NCEP-CFSv2 | NCEP Climate Forecast System Version 2 reanalysis dataset | VRE | Variable renewable energies |
| NL | Net load | Surplus of VRE energy generation regarding the annual electricity consumption | |
| NWP | Numerical weather prediction | w | Number of wind power regions identified using the cluster approach |
| Number of the it-th installations for the w-th region | Area need to install a 10 MW wind park | ||
| Number of the it-th installations for the s-th region | WindSTD | Scenario using only wind technology and the STD objective function | |
| PHS | Pumped hydro storage | WindHSC | Scenario using only wind technology and the HSC objective function |
| PV | Photovoltaic | Existing national aggregated wind hourly generation | |
| PVGIS | Photovoltaic geographical information system | WPP | Wind production patterns |
| PVSTD | Scenario using only solar PV technology and the STD objective function | Area available for additional wind power capacity deployment for the w-th region | |
| PVHSC | Scenario using only solar PV technology and the HSC objective function | Power production input matrix for clustering analysis | |
| PV + WindSTD | Scenario using only wind and solar PV technologies the STD objective function |
References
- Cucchiella, F.; D’Adamo, I.; Gastaldi, M. A profitability assessment of small-scale photovoltaic systems in an electricity market without subsidies. Energy Convers. Manag. 2016, 129, 62–74. [Google Scholar] [CrossRef]
- Abolhosseini, S.; Heshmati, A. The main support mechanisms to finance renewable energy development. Renew. Sustain. Energy Rev. 2014, 40, 876–885. [Google Scholar] [CrossRef] [Green Version]
- Niesten, E.; Jolink, A.; Chappin, M. Investments in the Dutch onshore wind energy industry: A review of investor profiles and the impact of renewable energy subsidies. Renew. Sustain. Energy Rev. 2018, 81, 2519–2525. [Google Scholar] [CrossRef] [Green Version]
- Arantegui, R.L.; Jäger-Waldau, A. Photovoltaics and wind status in the European Union after the Paris Agreement. Renew. Sustain. Energy Rev. 2018, 81, 2460–2471. [Google Scholar] [CrossRef]
- Shivakumar, A.; Dobbins, A.; Fahl, U.; Singh, A. Drivers of renewable energy deployment in the EU: An analysis of past trends and projections. Energy Strategy Rev. 2019, 26, 100402. [Google Scholar] [CrossRef]
- Kiviluoma, J.; Holttinen, H.; Weir, D.; Scharff, R.; Soder, L.; Menemenlis, N.; Cutululis, N.A.; Lopez, I.D.; Lannoye, E.; Estanqueiro, A.; et al. Variability in large-scale wind power generation. Wind Energy 2016, 19, 1649–1665. [Google Scholar] [CrossRef] [Green Version]
- Deetjen, T.A.; Rhodes, J.D.; Webber, M.E. The impacts of wind and solar on grid flexibility requirements in the Electric Reliability Council of Texas. Energy 2017, 123, 637–654. [Google Scholar] [CrossRef] [Green Version]
- Buttler, A.; Dinkel, F.; Franz, S.; Spliethoff, H. Variability of wind and solar power—An assessment of the current situation in the European Union based on the year 2014. Energy 2016, 106, 147–161. [Google Scholar] [CrossRef]
- Hansen, K.; Breyer, C.; Lund, H. Status and perspectives on 100% renewable energy systems. Energy 2019, 175, 471–480. [Google Scholar] [CrossRef]
- Gorjian, S.; Zadeh, B.N.; Eltrop, L.; Shamshiri, R.R.; Amanlou, Y. Solar photovoltaic power generation in Iran: Development, policies, and barriers. Renew. Sustain. Energy Rev. 2019, 106, 110–123. [Google Scholar] [CrossRef]
- Graabak, I.; Korpås, M. Variability Characteristics of European Wind and Solar Power Resources—A Review. Energies 2016, 9, 449. [Google Scholar] [CrossRef] [Green Version]
- Engeland, K.; Borga, M.; Creutin, J.-D.; François, B.; Ramos, M.-H.; Vidal, J.-P. Space-time variability of climate variables and intermittent renewable electricity production—A review. Renew. Sustain. Energy Rev. 2017, 79, 600–617. [Google Scholar] [CrossRef]
- Han, S.; Zhang, L.; Liu, Y.; Zhang, H.; Yan, J.; Li, L.; Lei, X.; Wang, X. Quantitative evaluation method for the complementarity of wind–solar–hydro power and optimization of wind–solar ratio. Appl. Energy 2019, 236, 973–984. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, Y.; Zhang, Y.; Terzija, V. Quantitative synergy assessment of regional wind-solar energy resources based on MERRA reanalysis data. Appl. Energy 2018, 216, 172–182. [Google Scholar] [CrossRef]
- Ren, G.; Wan, J.; Liu, J.; Yu, D. Spatial and temporal assessments of complementarity for renewable energy resources in China. Energy 2019, 177, 262–275. [Google Scholar] [CrossRef]
- Yan, J.; Qu, T.; Han, S.; Liu, Y.; Lei, X.; Wang, H. Reviews on characteristic of renewables: Evaluating the variability and complementarity. Int. Trans. Electr. Energy Syst. 2020, 30, e12281. [Google Scholar] [CrossRef]
- Gallardo, R.P.; Ríos, A.M.; Ramírez, J.S. Analysis of the solar and wind energetic complementarity in Mexico. J. Clean. Prod. 2020, 268, 122323. [Google Scholar] [CrossRef]
- Jurasz, J.; Canales, F.A.; Kies, A.; Guezgouz, M.; Beluco, A. A review on the complementarity of renewable energy sources: Concept, metrics, application and future research directions. Sol. Energy 2020, 195, 703–724. [Google Scholar] [CrossRef]
- Prasad, A.A.; Taylor, R.A.; Kay, M. Assessment of solar and wind resource synergy in Australia. Appl. Energy 2017, 190, 354–367. [Google Scholar] [CrossRef]
- Bett, P.E.; Thornton, H.E. The climatological relationships between wind and solar energy supply in Britain. Renew. Energy 2016, 87, 96–110. [Google Scholar] [CrossRef] [Green Version]
- Sterl, S.; Liersch, S.; Koch, H.; van Lipzig, N.P.M.; Thiery, W. A new approach for assessing synergies of solar and wind power: Implications for West Africa. Environ. Res. Lett. 2018, 13, 1–11. [Google Scholar] [CrossRef]
- Viviescas, C.; Lima, L.; Diuana, F.A.; Vasquez, E.; Ludovique, C.; Silva, G.N.; Huback, V.; Magalar, L.; Szklo, A.; Lucena, A.F.P.; et al. Contribution of variable renewable energy to increase energy security in Latin America: Complementarity and climate change impacts on wind and solar resources. Renew. Sustain. Energy Rev. 2019, 113, 109232. [Google Scholar] [CrossRef]
- Jerez, S.; Trigo, R.M.; Sarsa, A.; Lorente-Plazas, R.; Pozo-Vázquez, D.; Montávez, J.P. Spatio-temporal complementarity between solar and wind power in the Iberian Peninsula. Energy Procedia 2013, 40, 48–57. [Google Scholar] [CrossRef] [Green Version]
- Castro, R.; Crispim, J. Variability and correlation of renewable energy sources in the Portuguese electrical system. Energy Sustain. Dev. 2018, 42, 64–76. [Google Scholar] [CrossRef]
- Torres, P.J.F.; Ekonomou, L.; Karampelas, P. The correlation between renewable generation and electricity demand: A case study of Portugal. In Electricity Distribution. Energy Systems; Karampelas, P., Ekonomou, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 119–151. ISBN 978-3-662-49434-9. [Google Scholar]
- Simoes, S.; Zeyringer, M.; Mayr, D.; Huld, T.; Nijs, W.; Schmidt, J. Impact of different levels of geographical disaggregation of wind and PV electricity generation in large energy system models: A case study for Austria. Renew. Energy 2017, 105, 183–198. [Google Scholar] [CrossRef]
- Peter, J. How does climate change affect electricity system planning and optimal allocation of variable renewable energy? Appl. Energy 2019, 252, 113397. [Google Scholar] [CrossRef]
- Jurasz, J.; Dąbek, P.B.; Kaźmierczak, B.; Kies, A.; Wdowikowski, M. Large scale complementary solar and wind energy sources coupled with pumped-storage hydroelectricity for Lower Silesia (Poland). Energy 2018, 161, 183–192. [Google Scholar] [CrossRef]
- Blanco, H.; Faaij, A. A review at the role of storage in energy systems with a focus on Power to Gas and long-term storage. Renew. Sustain. Energy Rev. 2018, 81, 1049–1086. [Google Scholar] [CrossRef]
- Tafarte, P.; Eichhorn, M.; Thrän, D. Capacity expansion pathways for a wind and solar based power supply and the impact of advanced technology—A case study for Germany. Energies 2019, 12, 23. [Google Scholar] [CrossRef] [Green Version]
- Lorente-Plazas, R.; Montávez, J.P.; Jimenez, P.A.; Jerez, S.; Gómez-Navarro, J.J.; García-Valero, J.A.; Jimenez-Guerrero, P. Characterization of surface winds over the Iberian Peninsula. Int. J. Climatol. 2015, 35, 1007–1026. [Google Scholar] [CrossRef]
- Gutiérrez, C.; Gaertner, M.Á.; Perpiñán, O.; Gallardo, C.; Sánchez, E. A multi-step scheme for spatial analysis of solar and photovoltaic production variability and complementarity. Sol. Energy 2017, 158, 100–116. [Google Scholar] [CrossRef]
- Huth, R.; Beck, C.; Philipp, A.; Demuzere, M.; Ustrnul, Z.; Cahynová, M.; Kyselý, J.; Tveito, O.E. Classifications of atmospheric circulation patterns: Recent advances and applications. Ann. N. Y. Acad. Sci. 2008, 1146, 105–152. [Google Scholar] [CrossRef] [PubMed]
- Park, H.-S.; Jun, C.-H. A simple and fast algorithm for K-medoids clustering. Expert Syst. Appl. 2009, 36, 3336–3341. [Google Scholar] [CrossRef]
- Calinski, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 27. [Google Scholar]
- Da Luz, T.; Moura, P. Power generation expansion planning with complementarity between renewable sources and regions for 100% renewable energy systems. Int. Trans. Electr. Energy Syst. 2019, 29, 19. [Google Scholar]
- Vince, A. A framework for the greedy algorithm. Discret. Appl. Math. 2002, 121, 247–260. [Google Scholar] [CrossRef] [Green Version]
- Bird, L.; Lew, D.; Milligan, M.; Carlini, E.M.; Estanqueiro, A.; Flynn, D.; Gomez-Lazaro, E.; Holttinen, H.; Menemenlis, N.; Orths, A.; et al. Wind and solar energy curtailment: A review of international experience. Renew. Sustain. Energy Rev. 2016, 65, 577–586. [Google Scholar] [CrossRef] [Green Version]
- Boutsika, T.; Santoso, S. Quantifying Short-Term Wind Power Variability Using the Conditional Range Metric. IEEE Trans. Sustain. Energy 2012, 3, 369–378. [Google Scholar] [CrossRef]
- Couto, A.; Costa, P.; Rodrigues, L.; Lopes, V.V.; Estanqueiro, A. Impact of Weather Regimes on the Wind Power Ramp Forecast in Portugal. IEEE Trans. Sustain. Energy 2015, 6, 934–942. [Google Scholar] [CrossRef]
- REN. National Electric Grid Operator. Available online: http://www.centrodeinformacao.ren.pt/PT/Paginas/CIHomePage.aspx (accessed on 15 November 2019).
- Santos, J.; Corte-real, J.; Leite, S. Atmospheric large-scale dynamics during the 2004/2005 winter drought in Portugal. Int. J. Climatol. 2007, 586, 571–586. [Google Scholar] [CrossRef]
- Rodríguez-Benítez, F.J.; Arbizu-Barrena, C.; Santos-Alamillos, F.J.; Tovar-Pescador, J.; Pozo-Vázquez, D. Analysis of the intra-day solar resource variability in the Iberian Peninsula. Sol. Energy 2018, 171, 374–387. [Google Scholar] [CrossRef]
- Ulbrich, U.; Christoph, M.; Pinto, J.G.; Corte-Real, J. Dependence of winter precipitation over Portugal on NAO and baroclinic wave activity. Int. J. Climatol. 1999, 390, 379–390. [Google Scholar] [CrossRef]
- Hoinka, K.P.; de Castro, M. The Iberian Peninsula thermal low. Q. J. R. Meteorol. Soc. 2003, 129, 1491–1511. [Google Scholar] [CrossRef] [Green Version]
- Soares, P.M.M.; Cardoso, R.M.; Semedo, Á.; Chinita, M.J. Dynamic Meteorology and Oceanography Climatology of the Iberia coastal low-level wind jet: Weather research forecasting model high-resolution results. Tellus A Dyn. Meteorol. Oceanogr. 2014, 66, 22377. [Google Scholar] [CrossRef] [Green Version]
- Huber, M.; Dimkova, D.; Hamacher, T. Integration of wind and solar power in Europe: Assessment of flexibility requirements. Energy 2014, 69, 236–246. [Google Scholar] [CrossRef] [Green Version]
- Grell, G.; Dudhia, J.; Stauffer, D.R. A Description of the Fifth-Generation Penn State/NCAR Mesoscale Model (MM5); National Center for Atmospheric Research: Boulder, CO, USA, 1995; p. 121. [Google Scholar]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.; Iredell, M.; et al. NCEP Climate Forecast System Version 2 (CFSv2) 6-Hourly Products. Available online: https://rda.ucar.edu/datasets/ds094.0/ (accessed on 22 January 2019).
- Couto, A.; Silva, J.; Costa, P.; Santos, D.; Simões, T.; Estanqueiro, A. Towards a high-resolution offshore wind Atlas—The Portuguese case. J. Phys. Conf. Ser. 2019, 1356, 14. [Google Scholar] [CrossRef]
- Huld, T.; Mu, R. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Mueller, R.W.; Matsoukas, C.; Gratzki, A.; Behr, H.D.; Hollmann, R. The CM-SAF operational scheme for the satellite based retrieval of solar surface irradiance—A LUT based eigenvector hybrid approach. Remote Sens. Environ. 2009, 113, 1012–1024. [Google Scholar] [CrossRef]
- Urraca, R.; Gracia-Amillo, A.M.; Koubli, E.; Huld, T.; Trentmann, J.; Riihelä, A.; Lindfors, A.V.; Palmer, D.; Gottschalg, R.; Antonanzas-Torres, F. Extensive validation of CM SAF surface radiation products over Europe. Remote Sens. Environ. 2017, 199, 171–186. [Google Scholar] [CrossRef] [Green Version]
- Psiloglou, B.E.; Kambezidis, H.D.; Kaskaoutis, D.G.; Karagiannis, D.; Polo, J.M. Comparison between MRM simulations, CAMS and PVGIS databases with measured solar radiation components at the Methoni station, Greece. Renew. Energy 2020, 146, 1372–1391. [Google Scholar] [CrossRef]
- Lacerda, M.; Couto, A.; Estanqueiro, A. Wind power ramps driven by windstorms and cyclones. Energies 2017, 10, 1475. [Google Scholar] [CrossRef] [Green Version]
- Brummer, B.; Lange, I.; Konow, H. Atmospheric boundary layer measurements at the 280 m high Hamburg weather mast 1995–2011: Mean annual and diurnal cycles. Meteorol. Z. 2012, 21, 319–335. [Google Scholar] [CrossRef]
- Emeis, S. Current issues in wind energy meteorology. Meteorol. Appl. 2014, 21, 803–819. [Google Scholar] [CrossRef]
- Obi, M.; Bass, R. Trends and challenges of grid-connected photovoltaic systems—A review. Renew. Sustain. Energy Rev. 2016, 58, 1082–1094. [Google Scholar] [CrossRef]
- Hou, Q.; Zhang, N.; Du, E.; Miao, M.; Peng, F.; Kang, C. Probabilistic duck curve in high PV penetration power system: Concept, modeling, and empirical analysis in China. Appl. Energy 2019, 242, 205–215. [Google Scholar] [CrossRef]
- International Renewable Energy Agency. Renewable Power Generation Costs in 2018; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Abrell, J.; Kosch, M.; Rausch, S. Carbon abatement with renewables: Evaluating wind and solar subsidies in Germany and Spain. J. Public Econ. 2019, 169, 172–202. [Google Scholar] [CrossRef]
- Odeh, R.P.; Watts, D. Impacts of wind and solar spatial diversification on its market value: A case study of the Chilean electricity market. Renew. Sustain. Energy Rev. 2019, 111, 442–461. [Google Scholar] [CrossRef]













| Scenarios | Objective Function–Optimization Perspective | Technology (ies) Used | |
|---|---|---|---|
| STD | WindSTD | Minimize net load annual variability by adding: | Wind |
| PVSTD | Solar PV | ||
| PV + WindSTD | Solar PV + Wind | ||
| HSC | WindHSC | Minimize one-hour net load step change standard deviation by adding: | Wind |
| PVHSC | Solar PV | ||
| PV + WindHSC | Solar PV + Wind | ||
| Season | Current | PV + Wind | Wind | PV | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| STD | HSC | STD | HSC | STD | HSC | ||||||||
| 5% | 10% | 5% | 10% | 5% | 10% | 5% | 10% | 5% | 10% | 5% | 10% | ||
| Winter | 8.07 | 7.74 | 7.58 | 7.49 | 7.37 | 7.42 | 7.23 | 7.51 | 7.38 | 8.07 | 8.07 | 8.07 | 8.07 |
| Spring | 6.77 | 6.37 | 6.25 | 6.25 | 6.17 | 6.25 | 6.11 | 6.25 | 6.17 | 6.77 | 6.77 | 6.77 | 6.77 |
| Summer | 5.97 | 5.16 | 5.01 | 4.95 | 4.82 | 5.79 | 5.71 | 5.75 | 5.67 | 5.97 | 5.97 | 5.97 | 5.97 |
| Autumn | 6.67 | 6.43 | 6.39 | 6.25 | 6.17 | 6.26 | 6.17 | 6.29 | 6.21 | 6.67 | 6.67 | 6.67 | 6.67 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Couto, A.; Estanqueiro, A. Exploring Wind and Solar PV Generation Complementarity to Meet Electricity Demand. Energies 2020, 13, 4132. https://doi.org/10.3390/en13164132
Couto A, Estanqueiro A. Exploring Wind and Solar PV Generation Complementarity to Meet Electricity Demand. Energies. 2020; 13(16):4132. https://doi.org/10.3390/en13164132
Chicago/Turabian StyleCouto, António, and Ana Estanqueiro. 2020. "Exploring Wind and Solar PV Generation Complementarity to Meet Electricity Demand" Energies 13, no. 16: 4132. https://doi.org/10.3390/en13164132
APA StyleCouto, A., & Estanqueiro, A. (2020). Exploring Wind and Solar PV Generation Complementarity to Meet Electricity Demand. Energies, 13(16), 4132. https://doi.org/10.3390/en13164132