Quantifying the Demand Response Potential of Inherent Energy Storages in Production Systems
Abstract
:1. Introduction
Related Work
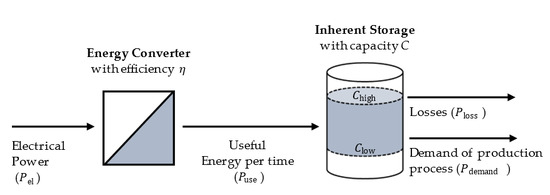
2. Modelling of IES
- electrical power required by the energy converter,
- : efficiency of the converter in the conversion of electricity into useful energy,
- generated useful energy per time,
- : the theoretical storage capacity,
- upper level of usable storage capacity (upper level of storage content),
- lower level of usable storage capacity (lower level of storage content),
- losses per time,
- energy demand per time of the production process.
2.1. Examples for IES in Production
2.2. General Remarks on the Calculation of the Flexibility Potential Calculation for IES
- to : Activation time (from first load change to reach of final load level)
- to : Holding time (constant load level)
- to : Deactivation time (from load level to zero)
- to : Break time (time until load recovery starts)
- to : Regeneration time (time until load recovery is completed)
2.3. Reference Load Profile
2.4. Calling a Flexibility Measure
2.5. Method for Quantifying the State-Dependent Flexibility Potential of IES
3. Case Study
- ▪
- Compressor: Increase of the upper pressure level up to 8 bar possible
- ▪
- Cleaning machine: Extension of the upper hysteresis limit up to 68 °C is possible
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Connolly, D.; Lund, H.; Mathiesen, B.V. Smart Energy Europe: The technical and economic impact of one potential 100% renewable energy scenario for the European Union. Renew. Sustain. Energy Rev. 2016, 60, 1634–1653. [Google Scholar] [CrossRef]
- Samad, T.; Koch, E.; Stluka, P. Automated Demand Response for Smart Buildings and Microgrids: The State of the Practice and Research Challenges. Proc. IEEE 2016, 104, 726–744. [Google Scholar] [CrossRef]
- Ulbig, A.; Andersson, G. Analyzing operational flexibility of electric power systems. Int. J. Electr. Power Energy Syst. 2015, 72, 155–164. [Google Scholar] [CrossRef]
- Alizadeh, M.I.; Parsa Moghaddam, M.; Amjady, N.; Siano, P.; Sheikh-El-Eslami, M.K. Flexibility in future power systems with high renewable penetration: A review. Renew. Sustain. Energy Rev. 2016, 57, 1186–1193. [Google Scholar] [CrossRef]
- BDEW. Stromverbrauch in Deutschland Nach Verbrauchergruppen 2019. Available online: https://www.bdew.de/media/documents/Nettostromverbrauch_nach_Verbrauchergruppen_2019_online_o_jaehrlich_Ki_12032020.pdf (accessed on 22 April 2020).
- Torriti, J.; Hassan, M.G.; Leach, M. Demand response experience in Europe: Policies, programmes and implementation. Energy 2010, 35, 1575–1583. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Shen, J.; Wang, X.; Jiang, C. From controllable loads to generalized demand-side resources: A review on developments of demand-side resources. Renew. Sustain. Energy Rev. 2016, 53, 936–944. [Google Scholar] [CrossRef]
- Council of the EU Directive (EU). 2019/944 on Common Rules for the Internal Market for Electricity and Amending Directive 2012/27/EU: 2019. Available online: https://eur-lex.europa.eu/eli/dir/2019/944/oj (accessed on 10 August 2020).
- Wattjes, F.D.; Janssen, S.L.L.; Slootweg, J.G. Framework for estimating flexibility of commercial and industrial customers in Smart Grids. In Proceedings of the IEEE PES ISGT Europe 2013, Lyngby, Denmark, 6–9 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–5. [Google Scholar]
- Petersen, M.K.; Edlund, K.; Hansen, L.H.; Bendtsen, J.; Stoustrup, J. A taxonomy for modeling flexibility and a computationally efficient algorithm for dispatch in Smart Grids. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1150–1156. [Google Scholar]
- Deng, R.; Yang, Z.; Chow, M.-Y.; Chen, J. A Survey on Demand Response in Smart Grids: Mathematical Models and Approaches. IEEE Trans. Ind. Inf. 2015, 11, 570–582. [Google Scholar] [CrossRef]
- VDI. Energieflexible Fabrik: Grundlagen (VDI 5207 Blatt 1); Beuth Verlag: Berlin, Germany, 2019. [Google Scholar]
- Schoepf, M.; Weibelzahl, M.; Nowka, L. The Impact of Substituting Production Technologies on the Economic Demand Response Potential in Industrial Processes. Energies 2018, 11, 2217. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Hug, G.; Kolter, Z.; Harjunkoski, I. Industrial demand response by steel plants with spinning reserve provision. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Zhang, X.; Hug, G.; Harjunkoski, I. Cost-Effective Scheduling of Steel Plants with Flexible EAFs. IEEE Trans. Smart Grid 2017, 8, 239–249. [Google Scholar] [CrossRef]
- Otashu, J.I.; Baldea, M. Scheduling chemical processes for frequency regulation. Appl. Energy 2020, 260, 114125. [Google Scholar] [CrossRef]
- Bohlayer, M.; Fleschutz, M.; Braun, M.; Zöttl, G. Energy-intense production-inventory planning with participation in sequential energy markets. Appl. Energy 2020, 258, 113954. [Google Scholar] [CrossRef]
- Summerbell, D.L.; Khripko, D.; Barlow, C.; Hesselbach, J. Cost and carbon reductions from industrial demand-side management: Study of potential savings at a cement plant. Appl. Energy 2017, 197, 100–113. [Google Scholar] [CrossRef]
- Rohde, C. Erstellung von Anwendungsbilanzen für die Jahre 2018 bis 2020 für die Sektoren Industrie und GHD; Fraunhofer Society: Karlsruhe, Germany, 2019. [Google Scholar]
- Shoreh, M.H.; Siano, P.; Shafie-khah, M.; Loia, V.; Catalão, J.P.S. A survey of industrial applications of Demand Response. Electr. Power Syst. Res. 2016, 141, 31–49. [Google Scholar] [CrossRef]
- Eisenhauer, S.; Reichart, M.; Sauer, A.; Weckmann, S.; Zimmernann, F. Energieflexibilität in der Industrie: Eine Metastudie; Institut für Energieeffizienz in der Produktion, Universität Stuttgart: Stuttgart, Germany, 2018. [Google Scholar]
- Conte, F.; Massucco, S.; Silvestro, F.; Ciapessoni, E.; Cirio, D. Stochastic modelling of aggregated thermal loads for impact analysis of demand side frequency regulation in the case of Sardinia in 2020. Int. J. Electr. Power Energy Syst. 2017, 93, 291–307. [Google Scholar] [CrossRef]
- Wai, C.H.; Beaudin, M.; Zareipour, H.; Schellenberg, A.; Lu, N. Cooling Devices in Demand Response: A Comparison of Control Methods. IEEE Trans. Smart Grid 2015, 6, 249–260. [Google Scholar] [CrossRef]
- Koch, S.; Zima, M.; Andersson, G. Active Coordination of Thermal Household Appliances for Load Management Purposes. IFAC Proc. Vol. 2009, 42, 149–154. [Google Scholar] [CrossRef] [Green Version]
- Rui, X.; Liu, X.; Meng, J. Dynamic Frequency Regulation Method Based on Thermostatically Controlled Appliances in the Power System. Energy Procedia 2016, 88, 382–388. [Google Scholar] [CrossRef] [Green Version]
- van der Heijde, B.; Sourbron, M.; Arance, F.V.; Salenbien, R.; Helsen, L. Unlocking flexibility by exploiting the thermal capacity of concrete core activation. Energy Procedia 2017, 135, 92–104. [Google Scholar] [CrossRef] [Green Version]
- Stadler, I. Demand Response: Nichtelektrische Speicher für Elektrizitätsversorgungssysteme mit Hohem Anteil Erneuerbarer Energien; Habilitation, der Universität Kassel: Berlin, Germany, October 2006. [Google Scholar]
- Koch, S.; Mathieu, J.; Callaway, D.S. Modeling and control of aggregated heterogeneous thermostatically controlled loads for ancillary services. Proc. PSCC 2011, 1–7. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.460.6240 (accessed on 10 August 2020).
- Sterner, M.; Stadler, I. Energiespeicher-Bedarf, Technologien, Integration; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Bundesamt für Energie BFE. Kälte Effizient Erzeugen: Das Wichtigste Zur kälteerzeugung Nach SIE 382/1; Bern, Switzerland, 2016; Available online: https://pubdb.bfe.admin.ch/de/publication/download/8559 (accessed on 10 August 2020).
- Gloor, R. Druckluftsysteme: Kennzahlen und Informationen über Energiesparmöglichkeiten bei Druckluftanlagen. Available online: https://energie.ch/druckluft/ (accessed on 24 April 2020).
- DIN Deutsches Institut für Normung e.V. Energetische Bewertung von Gebäuden—Lüftung von Gebäuden: Teil 3: Lüftung von Nichtwohngebäuden (DIN EN 16798-3:2017); Beuth Verlag GmbH: Berlin, Germany, 2017. [Google Scholar]
- Kuhrke, B. Methode Zur Energie-und Medienbedarfsbewertung Spanender Werkzeugmaschinen. Zugl.: Darmstadt. Ph.D. Dissertation, Technival University of Darmstadt, Berlin, Germany, 2011. [Google Scholar]
- Heemels, W.; Lehmann, D.; Lunze, J.; Schutter, B. Introduction to hybrid systems. In Handbook of Hybrid Systems Control: Theory, Tools, Applications; Cambridge University Press: Cambridge, UK, 2009; pp. 3–30. [Google Scholar]
- European Network of Transmission System Operators for Electricity (ENTSO-E). Electricity Balancing in Europe: An Overview of the European Balancing Market and Electricity Balancing Guideline; ENTSO-E: Brussels, Belgium, 2018. [Google Scholar]
- Oldewurtel, F.; Borsche, T.; Bucher, M.; Fortenbacher, P.; Gonzalez Vaya, M.; Haring, T.; Mathieu, J.L.; Mégel, O.; Vrettos, E.; Andersson, G. A framework for and assessment of demand response and energy storage in power systems. In Proceedings of the 2013 IREP Symposium Bulk Power System Dynamics and Control-IX Optimization, Security and Control of the Emerging Power Grid, Rethymnon, Crete, Greece, 25–30 August 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–24. [Google Scholar]
- Moura, S.; Bendtsen, J.; Ruiz, V. Parameter identification of aggregated thermostatically controlled loads for smart grids using PDE techniques. Int. J. Control 2014, 87, 1373–1386. [Google Scholar] [CrossRef]
- Qu, Z.; Xu, C.; Ma, K.; Jiao, Z. Fuzzy Neural Network Control of Thermostatically Controlled Loads for Demand-Side Frequency Regulation. Energies 2019, 12, 2463. [Google Scholar] [CrossRef] [Green Version]
- Angeli, D.; Kountouriotis, P.-A. A Stochastic Approach to “Dynamic-Demand” Refrigerator Control. IEEE Trans. Contr. Syst. Technol. 2012, 20, 581–592. [Google Scholar] [CrossRef]
- Postnikov, A.; Albayati, I.M.; Pearson, S.; Bingham, C.; Bickerton, R.; Zolotas, A. Facilitating static firm frequency response with aggregated networks of commercial food refrigeration systems. Appl. Energy 2019, 251, 113357. [Google Scholar] [CrossRef]
- Popp, R.S.-H.; Liebl, C.; Zaeh, M.F. Energy Flexible Machine tool Components—An Investigation of Capabilities. Procedia CIRP 2016, 57, 692–697. [Google Scholar] [CrossRef]
- Xie, K.; Hui, H.; Ding, Y. Review of modeling and control strategy of thermostatically controlled loads for virtual energy storage system. Prot. Control Mod. Power Syst. 2019, 4, 23. [Google Scholar] [CrossRef]
- Abele, E.; Beck, M.; Flum, D.; Schraml, P.; Panten, N.; Junge, F.; Bauerdick, C.; Helfert, M.; Sielaff, T. Gemeinsamer Schlussbericht zum Projekt ETA-Fabrik Energieeffiziente Fabrik für Interdisziplinäre Technologie-und Anwendungsforschung; Technische Universität Darmstadt: Darmstadt, Germany, 2019. [Google Scholar]
- Sonnen. Technische Daten sonnenBatterie 10. Available online: https://media.sonnen.de/de/media/62/download/inline (accessed on 14 May 2020).
- Tesla. Powerwall: Die Powerwall-Ihr Stromspeicher. Available online: https://www.tesla.com/de_DE/powerwall (accessed on 14 May 2020).
- GSMArena. Apple iPhone 11. Available online: https://www.gsmarena.com/apple_iphone_11-9848.php (accessed on 15 May 2020).
- Osthoff, A. Test Lenovo ThinkPad T490s (i5, Low-Power-FHD) Laptop. Available online: https://www.notebookcheck.com/Test-Lenovo-ThinkPad-T490s-i5-Low-Power-FHD-Laptop.416248.0.html (accessed on 15 May 2019).
- VDI Zentrum Ressourceneffizienz. Ökologische und Ökonomische Bewertung des Ressourcenaufwands: Stationäre Energiespeichersysteme in der Industriellen Produktion, 2nd ed.; VDI Zentrum Ressourceneffizienz: Berlin, Germany, 2018. [Google Scholar]
- Arcos-Vargas, Á.; Canca, D.; Núñez, F. Impact of battery technological progress on electricity arbitrage: An application to the Iberian market. Appl. Energy 2020, 260, 114273. [Google Scholar] [CrossRef]
- Nier, H. Preisverfall bei Lithium-Ionen-Batterien. Available online: https://de.statista.com/infografik/20280/preisentwicklung-von-lithium-ionen-batterien/ (accessed on 4 August 2020).

















| SOC Indicator | Example | Typical Converter with Typical Efficiency | Formula for Inherent Storage Capacity 1 | |
|---|---|---|---|---|
| Temperature () | Heated water tank | Heating element 100% | [29] | |
| Temperature () | Machine cooling | Compression chiller 350% 2 | [27] | |
| Pressure () | Compressed air generation with buffer tank | Compressor 60% 3 | [27] 4 | |
| Concentration () | Ventilated hall with CO2-Sensor | Ventilation System 0.35–0.56 Wh/m3 5 | [27] | |
| Filling level () | Lifting pump in machine tool | Pump 55 Wh/m3 6 | [27] |
| 1 | Calculation of the amount of electrical energy consumed by the system (integral of the electrical load profile) |
| 2 | Measurement of the electrical load peak and average electrical power |
| 3 | Counting the full charging cycles in the considered time interval |
| 4 | Determination of the duration and load factor of the respective cycle (according to Formulas (11) and (12)) |
| 5 | Calculation of the maximum shiftable amount of energy per cycle as well as the call times in case of fixed hysteresis limits (according to Formulas (16) and (17)) |
| 6 | Extracting the hysteresis limits in standard operation mode from the measured data |
| 7 | Calculation of the possible flexibility potential by shifting the hysteresis limits (according to Formulas (19) and (23)) |
| Key Indicators | Compressor 04:00–07:30 | Compressor 08:00–16:00 | Cleaning Machine 08:00–16:00 |
|---|---|---|---|
| Electrical energy demand | 2.47 kWh | 29.40 kWh | 26.31 kWh |
| Peak load | 4.13 kW | 7.34 kW | 13.32 kW |
| Mean load | 0.70 kW | 3.80 kW | 3.37 kW |
| Number of full charging cycles | 4 | 99 | 19 |
| Mean cycle time () | 41.75 min | 4.8 min | 21.63 min |
| Mean load factor () | 8.4% | 69.7% | 25.8% |
| Maximum holding time of flexibility measure () | 3.22 min | 1.02 min | 4.12 min |
| Call time for load increase ( ) | 35.01 min | 0.44 min | 11.91 min |
| Call time for load reduction ( ) | 0.30 min | 2.35 min | 1.44 min |
| Shiftable energy amount per cycle () | 0.22 kWh | 0.12 kWh | 0.92 kWh |
| Total shiftable energy amount | 0.88 kWh | 11.88 kWh | 17.48 kWh |
| Share of flexible energy in energy demand | 35.6% | 40.1% | 66.3% |
| Key Indicators | Compressor 04:00–07:30 | Compressor 08:00–16:00 | Cleaning Machine 08:00–16:00 |
|---|---|---|---|
| Upper limit of SOC Indicator | 7.46 bar | 7.45 bar | 60.47 °C |
| Lower limit of SOC Indicator | 6.95 bar | 6.88 bar | 57.29 °C |
| Hysteresis range in normal operation | 0.51 bar | 0.57 bar | 3.18 °C |
| Limit value for the increase factor of energy content 1 | |||
| New possible hysteresis range 1 | 6.07 bar | 0.82 bar | 12.34 °C |
| New possible upper limit of SOC Indicator 1 | 13.53 bar | 8.27 bar | 72.81 °C |
| New upper limit of SOC Indicator 2 | 8.00 bar | 8.00 bar | 68 °C |
| Actual increase factor of the energy content 3 | |||
| Additional amount of energy |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strobel, N.; Fuhrländer-Völker, D.; Weigold, M.; Abele, E. Quantifying the Demand Response Potential of Inherent Energy Storages in Production Systems. Energies 2020, 13, 4161. https://doi.org/10.3390/en13164161
Strobel N, Fuhrländer-Völker D, Weigold M, Abele E. Quantifying the Demand Response Potential of Inherent Energy Storages in Production Systems. Energies. 2020; 13(16):4161. https://doi.org/10.3390/en13164161
Chicago/Turabian StyleStrobel, Nina, Daniel Fuhrländer-Völker, Matthias Weigold, and Eberhard Abele. 2020. "Quantifying the Demand Response Potential of Inherent Energy Storages in Production Systems" Energies 13, no. 16: 4161. https://doi.org/10.3390/en13164161
APA StyleStrobel, N., Fuhrländer-Völker, D., Weigold, M., & Abele, E. (2020). Quantifying the Demand Response Potential of Inherent Energy Storages in Production Systems. Energies, 13(16), 4161. https://doi.org/10.3390/en13164161