Temperature Analysis of the Stand-Alone and Building Integrated Photovoltaic Systems Based on Simulation and Measurement Data
Abstract
:1. Introduction
2. Mathematical Models Determining the Temperature of a Photovoltaic Module
2.1. Standard Model (Nominal Operating Cell Temperature (NOCT))
- Ta—ambient temperature (°C),
- G0—the in-plane irradiance (W/m2),
- G0,NOCT = 800 W/m2—the irradiance at which the NOCT is defined,
- Ta,NOCT = 20 °C—the ambient temperature at which the NOCT is defined and
- Tmod,NOCT = 44 °C–46 °C—the technology-dependent nominal operating cell temperature [10].
2.2. King Model
- a—the coefficient describing the effect of the radiation on the module temperature in the King model,
- b—the coefficient describing the effect of cooling by the wind in the King model and
- vf—the wind speed at a height of 10 meters (m/s).
2.3. Skoplaki Models
- ω—mounting coefficient defined as the ratio of the Ross parameter for the mounting situation at-hand to the Ross parameter for a well-ventilated free-standing case. It takes on the values of 1, 1.2, 1.8 or 2.4, respectively, for free-standing installations, flat roofs, sloping roofs and facade-integrated photovoltaics, and
- vw—the local wind speed around the module (m/s).
- hw—wind convection coefficient (W·m−2 °C−1);
- hw,NOCT—wind convection coefficient (W·m−2·°C−1) for wind speed at NOCT conditions, i.e., vw = 1 m/s;
- v—wind speed (m/s);
- τ∙α—the effective transmittance-absorbance product of the module;
- ηSTC—efficiency coefficient of maximal power under standard test conditions (STC): irradiance G0,STC = 1000 W/m2, ambient temperature Ta,STC = 25 °C and air mass AM = 1.5 and
- βSTC—temperature coefficient of maximal power (Pmax) under STC (%/°C); it is technology-dependent [25].
- Skoplaki 1:
- Skoplaki 2:
- Skoplaki 3:where:
- vw1—wind directions perpendicular (±45°) to the module’s surface, andwhere:
- vw2—wind directions parallel (±45°) to the module’s surface.
2.4. Faiman Model
- U0—coefficient describing the effect of the radiation on the module temperature (W·m−2·°C−1), and
- U1—coefficient describing the cooling by the wind (W·s·m−3·°C−1).
2.5. Mattei Models
- UPV(v)—thermal losses coefficient from module to the surroundings (W·m−2·°C−1).
- Mattei 1:
- Mattei 2:
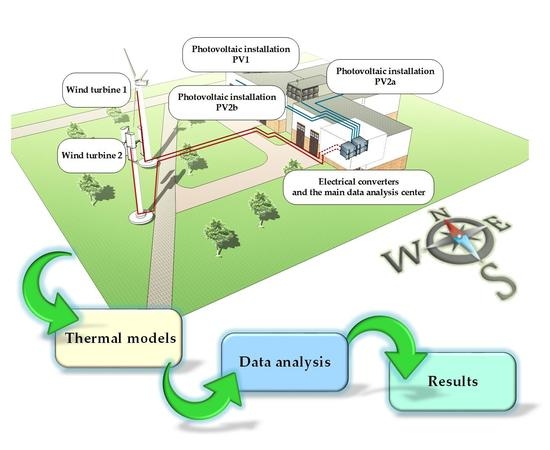
3. The Subject of the Research Description
4. The Analysis of Average Monthly and Daily Estimated Temperatures of the PV Modules
4.1. The Influence of Weather Conditions on the Operating Temperatures of PV Modules
4.2. The Parameters of Mathematical Models Found in the Literature
4.3. The Graphical Comparison of the Selected Models for Estimating the Temperatures of the PV Modules
4.4. Methodology and Data Analysis
- —the estimated value of the temperature,
- —the average value of the estimated temperature,
- —the observed (measured) value of the temperature,
- —the average value of the observed temperature,
- i—the summing index and
- n—the number of data used.
4.5. The Impact of Wind Speed
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alazab, M.; Khan, S.; Krishnan, S.S.R.; Pham, Q.V.; Reddy, M.P.K.; Gadekallu, T.R. A multidirectional LSTM model for predicting the stability of a smart grid. IEEE Access 2020, 8, 85454–85463. [Google Scholar] [CrossRef]
- Markvart, T. (Ed.) Solar Electricity, 2nd ed.; Wiley: Hoboken, NJ, USA, 2000; ISBN 978-0-471-98852-6. [Google Scholar]
- Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G.; Xiao, W. Photovoltaic Sources Modeling; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; ISBN 9781118679036. [Google Scholar]
- Xiao, W. Photovoltaic Power System: Modeling, Design, and Control; Wiley: Hoboken, NJ, USA, 2017; ISBN 9781119280347. [Google Scholar]
- Gökmen, N.; Hu, W.; Hou, P.; Chen, Z.; Sera, D.; Spataru, S. Investigation of wind speed cooling effect on PV panels in windy locations. Renew. Energy 2016, 90, 283–290. [Google Scholar] [CrossRef]
- Kusznier, J.; Wojtkowski, W. Impact of climatic conditions on PV panels operation in a photovoltaic power plant. In Proceedings of the 15th Selected Issues of Electrical Engineering and Electronics, WZEE 2019, Zakopane, Poland, 8–10 December 2019. [Google Scholar]
- Nkurikiyimfura, I.; Safari, B.; Nshingabigwi, E. A simulink model of photovoltaic modules under varying environmental conditions. IOP Conf. Ser. Earth Environ. Sci. 2018, 159, 012024. [Google Scholar] [CrossRef] [Green Version]
- Perovic, B.; Klimenta, D.; Jevtic, M.; Milovanovic, M. A transient thermal model for flat-plate photovoltaic systems and its experimental validation. Elektronika Ir Elektrotechnika 2019, 25, 40–46. [Google Scholar] [CrossRef] [Green Version]
- Mora Segado, P.; Carretero, J.; Sidrach-de-Cardona, M. Models to predict the operating temperature of different photovoltaic modules in outdoor conditions. Prog. Photovolt. Res. Appl. 2015, 23, 1267–1282. [Google Scholar] [CrossRef]
- Schwingshackl, C.; Petitta, M.; Wagner, J.E.; Belluardo, G.; Moser, D.; Castelli, M.; Zebisch, M.; Tetzlaff, A. Wind effect on PV module temperature: Analysis of different techniques for an accurate estimation. Energy Procedia 2013, 40, 77–86. [Google Scholar] [CrossRef] [Green Version]
- Veldhuis, A.J.; Nobre, A.; Reindl, T.; Ruther, R.; Reinders, A.H.M.E. The influence of wind on the temperature of PV modules in tropical environments, evaluated on an hourly basis. In Proceedings of the IEEE Photovoltaic Specialists Conference, Tampa, FL, USA, 16–21 June 2013. [Google Scholar]
- Frydrychowicz-Jastrzebska, G.; Bugała, A. Modeling the distribution of solar radiation on a two-axis tracking plane for photovoltaic conversion. Energies 2015, 8, 1025–1041. [Google Scholar] [CrossRef]
- Armstrong, S.; Hurley, W.G. A thermal model for photovoltaic panels under varying atmospheric conditions. Appl. Eng. 2010, 30, 1488–1495. [Google Scholar] [CrossRef]
- Chen, J.L.; He, L.; Yang, H.; Ma, M.; Chen, Q.; Wu, S.J.; Xiao, Z. Empirical models for estimating monthly global solar radiation: A most comprehensive review and comparative case study in China. Renew. Sustain. Energy Rev. 2019, 108, 91–111. [Google Scholar] [CrossRef]
- Idzkowski, A.; Walendziuk, W.; Borawski, W. Analysis of the temperature impact on the performance of photovoltaic panel. In Proceedings of the SPIE—The International Society for Optical Engineering; Romaniuk, R.S., Ed.; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9662, p. 96620. [Google Scholar]
- Kandemir, E.; Borekci, S.; Cetin, N.S. Conventional and soft-computing based MPPT methods comparisons in direct and indirect modes for single stage PV systems. Elektronika Ir Elektrotechnika 2018, 24, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Jaszczur, M.; Teneta, J.; Hassan, Q.; Majewska, E.; Hanus, R. An experimental and numerical investigation of photovoltaic module temperature under varying environmental conditions. Heat Transf. Eng. 2019. [Google Scholar] [CrossRef]
- Skoplaki, E.; Boudouvis, A.G.; Palyvos, J.A. A simple correlation for the operating temperature of photovoltaic modules of arbitrary mounting. Sol. Energy Mater. Sol. Cells 2008, 92, 1393–1402. [Google Scholar] [CrossRef]
- Mattei, M.; Notton, G.; Cristofari, C.; Muselli, M.; Poggi, P. Calculation of the polycrystalline PV module temperature using a simple method of energy balance. Renew. Energy 2006, 31, 553–567. [Google Scholar] [CrossRef]
- Faiman, D. Assessing the outdoor operating temperature of photovoltaic modules. Prog. Photovolt. Res. Appl. 2008, 16, 307–315. [Google Scholar] [CrossRef]
- King, D.L.; Boyson, W.E.; Kratochvil, J.A. Photovoltaic array performance model. Sandia Rep. 2004, 8, 1–41. [Google Scholar] [CrossRef] [Green Version]
- Koehl, M.; Heck, M.; Wiesmeier, S.; Wirth, J. Modeling of the nominal operating cell temperature based on outdoor weathering. Sol. Energy Mater. Sol. Cells 2011, 95, 1638–1646. [Google Scholar] [CrossRef]
- Kurtz, S.; Whitfield, K.; Miller, D.; Joyce, J.; Wohlgemuth, J.; Kempe, M.; Dhere, N.; Bosco, N.; Zgonena, T. Evaluation of high-temperature exposure of rack-mounted photovoltaic modules. In Proceedings of the 34th IEEE Photovoltaic Specialists Conference, Philadelphia, PA, USA, 7–12 June 2009. [Google Scholar]
- Mavromatakis, F.; Kavoussanaki, E.; Vignola, F.; Franghiadakis, Y. Measuring and estimating the temperature of photovoltaic modules. Sol. Energy 2014, 110, 656–666. [Google Scholar] [CrossRef]
- HOMER Energy. How HOMER Calculates the PV Array Power Output. Available online: https://www.homerenergy.com/products/pro/docs/latest/how_homer_calculates_the_pv_array_power_output.html (accessed on 13 June 2020).
- Bialystok University of Technology. Hybrid Power Plant of the Bialystok University of Technology. Available online: http://elektrownia.pb.edu.pl/ (accessed on 13 June 2020).
- European Commission. JRC Photovoltaic Geographical Information System (PVGIS)—European Commission. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/tools.html (accessed on 13 June 2020).
- Europe Solar Production. Polycrystalline Photovoltaic Module Europe Solar Production Premium Quality Solar Module Data Sheet ESP 6P 240-255 Wp. Available online: http://europe-solarproduction.com/media/690/ESP-Polycrystalline-Solar-Module-Datasheets-ESP-6P-series.pdf (accessed on 17 August 2020).
- SMA Solar Technology AG. SUNNY BOY 2000HF/2500HF/3000HF—Installation Guide. Available online: https://www.solartradesales.co.uk/Cache/Downloads/SunnyBoy-HF-Installation-guide-3.pdf (accessed on 17 August 2020).
- Solahart Goodwe Single Phase Small Domestic Inverter. GW1500-NS & GW3000-NS. Available online: https://www.solahart.com.au/media/5305/ih0113_gw1500-ns-gw3000-ns_single-phase-inverters_june-2019_web.pdf (accessed on 13 June 2020).
- Compact Weather Sensors—WS501-UMB Smart Weather Sensor. Available online: https://www.lufft.com/products/compact-weather-sensors-293/ws501-umb-smart-weather-sensor-1839/ (accessed on 24 July 2020).
- National Instruments. NI 9213 Datasheet. Available online: https://www.ni.com/pdf/manuals/378021a_02.pdf (accessed on 24 July 2020).
- National Instruments. NI 9219 Datasheet. Available online: https://www.ni.com/pdf/manuals/377223a_02.pdf (accessed on 24 July 2020).
- Delta OHM. LP Pyra 02—LP Pyra 03—LP Pyra 12. Available online: https://www.deltaohm.com/ver2012/download/LP_PYRA02_03_12_uk.pdf (accessed on 24 July 2020).












| Company | Europe Solar Production | |
| Model | ESP 250 6P | |
| Dimensions | 1640 × 990 × 40 | |
| Electrical Data at STC | ||
| Module Efficiency ηSTC | 15.3 | % |
| Peak Power Watts Pmax,STC | 250 | Wp |
| Maximum Power Voltage Vmpp,STC | 30.93 | V |
| Maximum Power Current Impp,STC | 8.08 | A |
| Electrical Data at NOCT | ||
| Peak Power Watts Pmax,NOCT | 182 | Wp |
| Maximum Power Voltage Vmpp,NOCT | 28.04 | V |
| Maximum Power Current Impp,NOCT | 6.49 | A |
| Temperatures Ratings | ||
| Temperature Coefficient of Pmax (βSTC) | −0.46 | %/°C |
| Temperature Coefficient of Open-Circuit Voltage VOC | −0.34 | %/°C |
| Temperature Coefficient of Short-Circuit Voltage Isc | 0.07 | %/°C |
| Company | SMA Solar Technology AG | GoodWe | ||
| Model | Sunny Boy 3000 HF | GW 1500-NS | ||
| DC Input | ||||
| Maximum Input Voltage | 700 | V | 500 | V |
| Minimum Input Voltage | 175 | V | 80 | V |
| Rated Input Voltage | 530 | V | 360 | V |
| MPP Voltage Range | 210–560 | V | 80–450 | V |
| Maximum Input Current | 15 | A | 10 | A |
| AC Output | ||||
| Maximum Output Current | 15 | A | 7.5 | A |
| Rated Power at 230 V, 50 Hz | 3000 | W | 1500 | W |
| Maximum Apparent AC Power | 3000 | VA | 1500 | VA |
| Efficiency | ||||
| Maximum efficiency ηmax | 96.3 | % | 97.0 | A |
| European weighted efficiency ηEU | 95.4 | % | 96.0 | W |
| Parameter | Measurement of PV Module Temperature NI-9213—Thermocouple Module, Voltage Measurement with Conversion to Temperature | Pyranometer Data Acquisition NI-9219—Universal Multipurpose Module, Voltage Measurement |
|---|---|---|
| Number of channels | 16 thermocouple channels | 4 analog input channels |
| Analog-to-digital converter (ADC) resolution | 24 bits | 24 bits |
| Type of ADC | Delta-sigma (with analog prefiltering) | Delta-sigma (with analog prefiltering) |
| Sampling rate | 1 S/s | 2 S/s |
| Gain error in high-resolution mode at −40 °C to 70 °C | 0.07% typical, 0.15% maximum | 0.3% typical, 0.4% maximum |
| Offset error in high-resolution mode at −40 °C to 70 °C | 4 μV typical, 6 μV maximum | 6 μV typical, 180 μV maximum |
| Other | Cold-junction compensation −40 °C to 70 °C 1.1 °C typical, 2.1 °C maximum | Stability of the gain drift ± 20 (ppm of reading/°C) |
| Parameter | Value |
|---|---|
| Class | second (ISO 9060) |
| Typical sensitivity | 10 μV/(W/m2) |
| Impedance | 33–45 Ω |
| Measuring range | 0 ÷ 2000 W/m2 |
| Viewing Field | 2π sr |
| Spectral Field | 305–2800 nm |
| Operating temperature | −40 °C–80 °C |
| Month | Average Wind Speed vw (m/s) | Average Ambient Temperature Ta (°C) | Average Irradiance G0 (W/m2) | Average Operating Temperature Tmod (°C) |
|---|---|---|---|---|
| I | 2.84 | −3.27 | 120.20 | 1.24 |
| II | 3.20 | 2.71 | 208.06 | 8.88 |
| III | 3.90 | 5.74 | 339.05 | 15.08 |
| IV | 2.95 | 11.95 | 556.20 | 27.81 |
| V | 2.16 | 10.68 | 310.34 | 20.10 |
| VI | 2.84 | 23.48 | 592.94 | 39.75 |
| VII | 3.20 | 18.95 | 445.28 | 31.28 |
| VIII | 2.22 | 20.60 | 533.60 | 36.37 |
| IX | 3.20 | 15.73 | 458.14 | 28.17 |
| X | 2.40 | 10.76 | 280.39 | 18.98 |
| XI | 2.84 | 5.29 | 66.38 | 8.54 |
| XII | 2.44 | 2.67 | 81.77 | 5.99 |
| Model | Parameter | Value | Quantities | |
|---|---|---|---|---|
| Faiman | U0 | 30.02 | W·m−2·°C−1 | |
| U1 | 6.28 | W·s·m−3·°C−1 | ||
| King | a | Stand-alone power system PV1 | −3.56 | - |
| Building-integrated power systems PV2a and PV2b | −2.81 | |||
| King | b | Stand-alone power system PV1 | −0.0750 | s·m−1 |
| Building-integrated power systems PV2a and PV2b | −0.0455 | |||
| Skoplaki | Stand-alone power system PV1 (flat-roof) | 1.2 | - | |
| Building-integrated power systems PV2a and PV2b | 2.4 (2.2-2.6) | |||
| Skoplaki 1 and 2 | τ·α | 0.90 | - | |
| Mattei 1 and 2 | 0.81 | |||
| PV1 | PV2a | PV2b | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NRMSE (%) | NMBE (%) | k (-) | NRMSE (%) | NMBE (%) | k (-) | NRMSE (%) | NMBE (%) | k (-) | |
| Standard | 8.27 | 5.31 | 1.00 | 20.16 | −19.53 | 1.00 | 10.24 | −8.05 | 1.00 |
| Skoplaki | 5.29 | −4.87 | 1.00 | 7.95 | 1.92 | 1.00 | 16.93 | 10.49 | 0.99 |
| Skoplaki 1 | 24.22 | 19.50 | 0.83 | 10.98 | −10.39 | 0.86 | 9.00 | −0.18 | 0.90 |
| Skoplaki 2 | 53.39 | 44.96 | 0.99 | 12.07 | 6.06 | 0.99 | 20.60 | 14.03 | 0.99 |
| Faiman/Koehl | 14.53 | −13.82 | 1.00 | 33.65 | −31.93 | 1.00 | 19.35 | −18.83 | 1.00 |
| Mattei 1 | 22.72 | −7.92 | 0.98 | 42.98 | −33.49 | 0.98 | 40.48 | −30.07 | 0.95 |
| Mattei 2 | 22.60 | −7.35 | 0.98 | 42.83 | −33.19 | 0.98 | 40.56 | −29.92 | 0.95 |
| King | 52.99 | −47.89 | 0.98 | 58.09 | −53.96 | 0.97 | 39.22 | −37.92 | 0.99 |
| PV1 | PV2a | PV2b | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NRMS E (%) | NMBE (%) | k (-) | NRMSE (%) | NMBE (%) | k (-) | NRMSE (%) | NMBE (%) | k (-) | |
| Standard | 12.75 | 7.99 | 0.96 | 20.44 | −16.63 | 0.90 | 9.43 | −6.81 | 0.97 |
| Skoplaki | 5.93 | −4.92 | 0.99 | 14.49 | 10.30 | 0.97 | 20.34 | 17.88 | 0.96 |
| Skoplaki 1 | 26.49 | 24.43 | 0.48 | 8.63 | −5.44 | 0.52 | 8.73 | 3.76 | 0.56 |
| Skoplaki 2 | 59.69 | 55.58 | 0.94 | 20.34 | 16.00 | 0.97 | 27.12 | 23.32 | 0.91 |
| Faiman/Koehl | 16.20 | −15.67 | 0.99 | 34.29 | −33.09 | 0.95 | 22.08 | −21.25 | 0.97 |
| Mattei 1 | 22.21 | −15.48 | 0.98 | 41.39 | −37.80 | 0.89 | 39.05 | −34.85 | 0.88 |
| PV1 | PV2a | PV2b | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NRMS E (%) | NMBE (%) | k (-) | NRMSE (%) | NMBE (%) | k (-) | NRMSE (%) | NMBE (%) | k (-) | |
| Standard | 8.28 | 6.43 | 0.99 | 14.81 | −13.93 | 0.98 | 8.27 | −4.87 | 0.99 |
| Skoplaki | 3.01 | −0.87 | 1.00 | 9.03 | 4.98 | 0.96 | 16.36 | 13.40 | 0.99 |
| Skoplaki 1 | 24.20 | 22.48 | 0.98 | 7.77 | −5.03 | 0.98 | 6.16 | 4.37 | 0.97 |
| Skoplaki 2 | 52.01 | 48.56 | 0.96 | 13.92 | 9.79 | 0.94 | 24.22 | 18.72 | 0.98 |
| Faiman/Koehl | 9.64 | −9.32 | 1.00 | 23.91 | −23.31 | 0.98 | 15.47 | −12.65 | 0.98 |
| Mattei 1 | 29.87 | −27.84 | 0.99 | 48.43 | −47.28 | 0.77 | 47.33 | −44.93 | 0.93 |
| PV1 | PV2a | PV2b | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NRMSE (%) | NMBE (%) | k (-) | NRMSE (%) | NMBE (%) | k (-) | NRMSE (%) | NMBE (%) | k (-) | |
| Standard | 7.16 | 3.67 | 0.98 | 17.95 | −17.03 | 0.98 | 5.04 | −3.76 | 0.99 |
| Skoplaki | 2.90 | −0.46 | 1.00 | 12.73 | 8.34 | 0.97 | 18.28 | 15.99 | 0.98 |
| Skoplaki 1 | 28.08 | 25.00 | 0.94 | 7.43 | −3.02 | 0.92 | 9.23 | 7.06 | 0.93 |
| Skoplaki 2 | 62.04 | 55.84 | 0.96 | 22.94 | 17.18 | 0.96 | 26.32 | 22.75 | 0.96 |
| Faiman/Koehl | 9.74 | −9.50 | 1.00 | 26.63 | −25.57 | 0.97 | 11.41 | −10.56 | 0.98 |
| Mattei 1 | 27.44 | −24.50 | 0.98 | 46.13 | −43.52 | 0.93 | 43.80 | −40.68 | 0.82 |
| PV1 | PV2a | PV2b | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NRMSE (%) | NMBE (%) | k (-) | NRMSE (%) | NMBE (%) | k (-) | NRMSE (%) | NMBE (%) | k (-) | |
| Standard | 11.25 | 8.78 | 0.98 | 14.56 | −12.70 | 0.97 | 6.44 | −1.83 | 0.97 |
| Skoplaki | 3.75 | −1.98 | 1.00 | 16.34 | 9.28 | 0.96 | 19.49 | 15.77 | 0.97 |
| Skoplaki 1 | 26.14 | 21.69 | 0.56 | 9.96 | −3.65 | 0.59 | 9.23 | 5.23 | 0.66 |
| Skoplaki 2 | 54.78 | 46.42 | 0.96 | 22.23 | 13.59 | 0.93 | 23.92 | 19.15 | 0.96 |
| Faiman/Koehl | 11.32 | −10.68 | 1.00 | 28.34 | −26.21 | 0.94 | 14.62 | −13.08 | 0.97 |
| Mattei 1 | 21.84 | −14.64 | 0.97 | 39.54 | −34.61 | 0.89 | 37.03 | −31.68 | 0.72 |
| PV2a | PV2b | |||
|---|---|---|---|---|
| NRMSE (%) | NRMSE (%) | NRMSE (%) | NRMSE (%) | |
| April | 14.49 | 7.81 | 20.34 | 10.54 |
| June | 9.03 | 6.67 | 16.36 | 7.94 |
| August | 12.73 | 6.86 | 18.28 | 10.64 |
| September | 16.34 | 9.72 | 19.49 | 11.36 |
| whole year 2019 | 7.95 | 8.41 | 16.93 | 10.24 |
| PV2a | PV2b | |||
|---|---|---|---|---|
| NMBE (%) | NMBE (%) | NMBE (%) | NMBE (%) | |
| April | 10.30 | −1.69 | 17.88 | 7.07 |
| June | 4.98 | −2.82 | 13.40 | 6.22 |
| August | 8.34 | −0.99 | 15.99 | 8.68 |
| September | 9.28 | −0.53 | 15.77 | 7.80 |
| whole year 2019 | 1.92 | −7.43 | 10.49 | 2.38 |
| Installation Name and Date | Faiman | Skoplaki | Skoplaki* | Skoplaki 1 | Mattei 1 | Wind Speed | Module and Ambient Temp. | Irradiance |
|---|---|---|---|---|---|---|---|---|
(°C) | (°C) | (°C) | (°C) | (°C) | (m/s) | (°C) | (W/m2) | |
| PV1: 24 Aug. | 4.3 | −1.4 | −1.4 | −18.4 | 17.6 | 1.0 | 47.9; 22.8 | 755.5 |
| PV1: 28 Aug. | 3.1 | −1.1 | −1.1 | −12.6 | 13.6 | 2.7 | 44.5; 25.4 | 750.5 |
| PV2a: 24 Aug. | 13.1 | −9.0 | −3.0 (= 2) | −2.5 | 26.8 | 1.0 | 50.1; 22.8 | 518.6 |
| PV2a: 28 Aug. | 9.9 | −7.5 | −2.7 (= 2) | −1.2 | 21.9 | 2.7 | 46.8; 25.4 | 534.7 |
| PV2b: 24 Aug. | 3.1 | −10.2 | −6.6 (= 2) | −6.3 | 17.2 | 1.0 | 34.4; 22.8 | 311.8 |
| PV2b: 28 Aug. | 5.0 | −5.0 | −2.2 (= 2) | −1.4 | 18.6 | 2.7 | 37.0; 25.4 | 315.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Idzkowski, A.; Karasowska, K.; Walendziuk, W. Temperature Analysis of the Stand-Alone and Building Integrated Photovoltaic Systems Based on Simulation and Measurement Data. Energies 2020, 13, 4274. https://doi.org/10.3390/en13164274
Idzkowski A, Karasowska K, Walendziuk W. Temperature Analysis of the Stand-Alone and Building Integrated Photovoltaic Systems Based on Simulation and Measurement Data. Energies. 2020; 13(16):4274. https://doi.org/10.3390/en13164274
Chicago/Turabian StyleIdzkowski, Adam, Karolina Karasowska, and Wojciech Walendziuk. 2020. "Temperature Analysis of the Stand-Alone and Building Integrated Photovoltaic Systems Based on Simulation and Measurement Data" Energies 13, no. 16: 4274. https://doi.org/10.3390/en13164274
APA StyleIdzkowski, A., Karasowska, K., & Walendziuk, W. (2020). Temperature Analysis of the Stand-Alone and Building Integrated Photovoltaic Systems Based on Simulation and Measurement Data. Energies, 13(16), 4274. https://doi.org/10.3390/en13164274