Electrical Response of Mechanically Damaged Lithium-Ion Batteries
Abstract
:1. Introduction
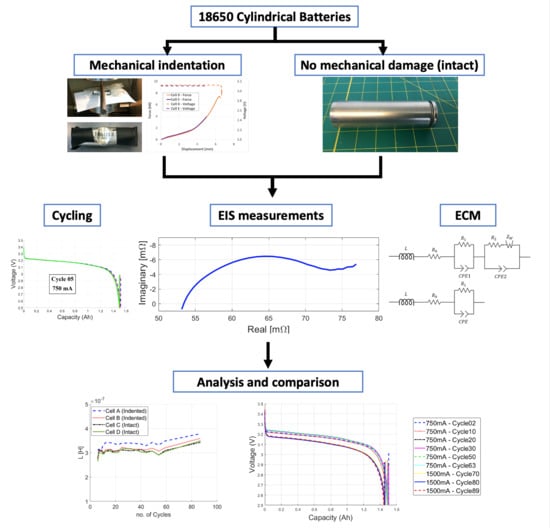
- Investigate the effects of mechanical deformation that does not lead to immediate failure of cells on the electrical performance of battery cells.
- Collect data on charge-discharge cycling, capacity fade rate, and Electrochemical Impedance Spectroscopy to track potential changes in the response of the cell.
- Use nonlinear modeling with distributed CPE elements to achieve very small fitting error to accurately represent impedance spectra of the cells and interpret the results.
- Show trend of changes in cell parameters for mechanically damaged versus intact cells over low and high rate cycling.
2. Modeling Using Impedance Spectra
2.1. Electrochemical Impedance Spectroscopy
2.2. Equivalent Circuit Model
3. Experimental Procedure
3.1. Mechanical Loading
3.2. Cycling Procedure
3.3. EIS Measurements
4. Results
4.1. Battery Cycling Data
4.2. EIS Results
4.3. High-Rate Testing
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wei, Z.; Zou, C.; Leng, F.; Soong, B.H.; Tseng, K. Online Model Identification and State-of-Charge Estimate for Lithium-Ion Battery With a Recursive Total Least Squares-Based Observer. IEEE Trans. Ind. Electron. 2018, 65, 1336–1346. [Google Scholar] [CrossRef]
- Barai, A.; Chouchelamane, G.H.; Guo, Y.; McGordon, A.; Jennings, P. A Study on the Impact of Lithium-Ion Cell Relaxation on Electrochemical Impedance Spectroscopy. J. Power Sources 2015, 280, 74–80. [Google Scholar] [CrossRef]
- Willard, N.; He, W.; Hendricks, C.; Pecht, M. Lessons Learned from the 787 Dreamliner Issue on Lithium-Ion Battery Reliability. Energies 2013, 6, 4682–4695. [Google Scholar] [CrossRef] [Green Version]
- Feng, X.; Sun, J.; Ouyang, M.; Wang, F.; He, X.; Lu, L.; Peng, H. Characterization of penetration induced thermal runaway propagation process within a large format lithium ion battery module. J. Power Sources 2015, 275, 261–273. [Google Scholar] [CrossRef]
- Smith, B. Chevrolet Volt Battery Incident Overview Report; Technical Report; DOT HS 811 573; NHTSA: Washington, DC, USA, 2012.
- Kermani, G.; Sahraei, E. Review: Characterization and Modeling of the Mechanical Properties of Lithium-Ion Batteries. Energies 2017, 10, 1730. [Google Scholar] [CrossRef] [Green Version]
- Kermani, G.; Sahraei, E. Dynamic impact response of lithium-ion batteries, constitutive properties and failure model. RSC Adv. 2019, 9, 2464–2473. [Google Scholar] [CrossRef] [Green Version]
- Sahraei, E.; Campbell, J.; Wierzbicki, T. Modeling and short circuit detection of 18650 Li-ion cells under mechanical abuse conditions. J. Power Sources 2012, 220, 360–372. [Google Scholar] [CrossRef]
- Sahraei, E.; Hill, R.; Wierzbicki, T. Calibration and finite element simulation of pouch lithium-ion batteries for mechanical integrity. J. Power Sources 2012, 201, 307–321. [Google Scholar] [CrossRef]
- Greve, L.; Fehrenbach, C. Mechanical testing and macro-mechanical finite element simulation of the deformation, fracture, and short circuit initiation of cylindrical Lithium ion battery cells. J. Power Sources 2012, 214, 377–385. [Google Scholar] [CrossRef]
- Ali, M.Y.; Lai, W.J.; Pan, J. Computational Models for Simulations of Lithium-Ion Battery Cells under Constrained Compression Tests. J. Power Sources 2013, 242, 325–340. [Google Scholar] [CrossRef]
- Avdeev, I.; Gilaki, M. Structural Analysis and Experimental Characterization of Cylindrical Lithium-Ion Battery Cells Subject to Lateral Impact. J. Power Sources 2014, 271, 382–391. [Google Scholar] [CrossRef]
- Sahraei, E.; Meier, J.; Wierzbicki, T. Characterizing and modeling mechanical properties and onset of short circuit for three types of lithium-ion pouch cells. J. Power Sources 2014, 247, 503–516. [Google Scholar] [CrossRef]
- Gilaki, M.; Avdeev, I. Impact modeling of cylindrical lithium-ion battery cells: A heterogeneous approach. J. Power Sources 2016, 328, 443–451. [Google Scholar] [CrossRef]
- Xu, J.; Liu, B.; Hu, D. State of Charge Dependent Mechanical Integrity Behavior of 18650 Lithium-Ion Batteries. Sci. Rep. 2016, 6, 21829. [Google Scholar] [CrossRef] [Green Version]
- Kisters, T.; Sahraei, E.; Wierzbicki, T. Dynamic Impact Tests on Lithium-Ion Cells. Int. J. Impact Eng. 2017, 108, 205–216. [Google Scholar] [CrossRef]
- Dixon, B.; Mason, A.; Sahraei, E. Effects of Electrolyte, Loading Rate and Location of Indentation on Mechanical Integrity of Li-Ion Pouch Cells. J. Power Sources 2018, 396, 412–420. [Google Scholar] [CrossRef]
- Kermani, G.; Dixon, B.; Sahraei, E. Elliptical lithium-ion batteries: Transverse and axial loadings under wet/dry conditions. Energy Sci. Eng. 2019, 7, 890–898. [Google Scholar] [CrossRef] [Green Version]
- Gilaki, M.; Sahraei, E. Effects of Temperature on Mechanical Response of Lithium Ion Batteries to External Abusive Loads. In Proceedings of the SAE World Congress, Detroit, MI, USA, 9–11 April 2009. SAE Technical Paper. [Google Scholar]
- Zhang, X.; Zhu, J.; Sahraei, E. Degradation of Battery Separators under Charge–Discharge Cycles. RSC Adv. 2017, 7, 56099–56107. [Google Scholar] [CrossRef] [Green Version]
- Luo, H.; Zhu, J.; Sahraei, E.; Xia, Y. Adhesion Strength of the Cathode in Lithium-Ion Batteries under Combined Tension/Shear Loadings. RSC Adv. 2018, 8, 3996–4005. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Li, W.; Xia, Y.; Sahraei, E. Testing and Modeling the Mechanical Properties of the Granular Materials of Graphite Anode. J. Electrochem. Soc. 2018, 165, A1160. [Google Scholar] [CrossRef]
- Sahraei, E.; Kahn, M.; Meier, J.; Wierzbicki, T. Modelling of Cracks Developed in Lithium-Ion Cells under Mechanical Loading. RSC Adv. 2015, 5, 80369–80380. [Google Scholar] [CrossRef]
- Sahraei, E.; Bosco, E.; Dixon, B.; Lai, B. Microscale Failure Mechanisms Leading to Internal Short Circuit in Li-Ion Batteries under Complex Loading Scenarios. J. Power Sources 2016, 319, 56–65. [Google Scholar] [CrossRef]
- Sahraei, E.; Hill, R.L.; Wierzbicki, T. Modeling of Lithium-Ion Cylindrical Batteries for Mechanical Integrity: Experiments, Calibrations, and Validation. In Proceedings of the Battery Congress, Detroit MI, USA, 11–12 April 2011. [Google Scholar]
- Kalnaus, S.; Wang, H.; Watkins, T.R.; Kumar, A.; Simunovic, S.; Turner, J.A.; Gorney, P. Effect of packaging and cooling plates on mechanical response and failure characteristics of automotive Li-ion battery modules. J. Power Sources 2018, 403, 20–26. [Google Scholar] [CrossRef]
- Zhang, X.; Sahraei, E.; Wang, K. Li-Ion Battery Separators, Mechanical Integrity and Failure Mechanisms Leading to Soft and Hard Internal Shorts. Sci. Rep. 2016, 6, 32578. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Sahraei, E.; Wang, K. Deformation and Failure Characteristics of Four Types of Lithium-Ion Battery Separators. J. Power Sources 2016, 327, 693–701. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, X.; Luo, H.; Sahraei, E. Investigation of the Deformation Mechanisms of Lithium-Ion Battery Components Using in-Situ Micro Tests. Appl. Energy 2018, 224, 251–266. [Google Scholar] [CrossRef]
- Mikolajczak, C.; Kahn, M.; White, K.; Long, R.T. Lithium-Ion Batteries Hazard and Use Assessment; SpringerBriefs in Fire; Springer: Boston, MA, USA, 2011. [Google Scholar]
- Stephens, D.; Shawcross, P.; Stout, G.; Sullivan, E.; Saunders, J.; Risser, S.; Sayre, J. Lithium-Ion Battery Safety Issues for Electric and Plug-in Hybrid Vehicles; Technical Report DOT HS 812 418; National Highway Traffic Safety Administration: Washington, DC, USA, 2017.
- Li, Z.; Xiong, R.; Mu, H.; He, H.; Wang, C. A Novel Parameter and State-of-Charge Determining Method of Lithium-Ion Battery for Electric Vehicles. Appl. Energy 2017, 207, 363–371. [Google Scholar] [CrossRef]
- Zeng, Z.; Tian, J.; Li, D.; Tian, Y. An Online State of Charge Estimation Algorithm for Lithium-Ion Batteries Using an Improved Adaptive Cubature Kalman Filter. Energies 2018, 11, 59. [Google Scholar] [CrossRef] [Green Version]
- Xia, B.; Lao, Z.; Zhang, R.; Tian, Y.; Chen, G.; Sun, Z.; Wang, W.; Sun, W.; Lai, Y.; Wang, M.; et al. Online Parameter Identification and State of Charge Estimation of Lithium-Ion Batteries Based on Forgetting Factor Recursive Least Squares and Nonlinear Kalman Filter. Energies 2017, 11, 3. [Google Scholar] [CrossRef] [Green Version]
- Andre, D.; Meiler, M.; Steiner, K.; Wimmer, C.; Soczka-Guth, T.; Sauer, D. Characterization of High-Power Lithium-Ion Batteries by Electrochemical Impedance Spectroscopy. I. Experimental Investigation. J. Power Sources 2011, 196, 5334–5341. [Google Scholar] [CrossRef]
- Lohmann, N.; Weßkamp, P.; Haußmann, P.; Melbert, J.; Musch, T. Electrochemical Impedance Spectroscopy for Lithium-Ion Cells: Test Equipment and Procedures for Aging and Fast Characterization in Time and Frequency Domain. J. Power Sources 2015, 273, 613–623. [Google Scholar] [CrossRef]
- Cui, Y.; Zuo, P.; Du, C.; Gao, Y.; Yang, J.; Cheng, X.; Ma, Y.; Yin, G. State of Health Diagnosis Model for Lithium Ion Batteries Based on Real-Time Impedance and Open Circuit Voltage Parameters Identification Method. Energy 2018, 144, 647–656. [Google Scholar] [CrossRef]
- Chen, L.; Lü, Z.; Lin, W.; Li, J.; Pan, H. A New State-of-Health Estimation Method for Lithium-Ion Batteries through the Intrinsic Relationship between Ohmic Internal Resistance and Capacity. Measurement 2018, 116, 586–595. [Google Scholar] [CrossRef]
- Barsoukov, E.; Macdonald, J.R. (Eds.) Impedance Spectroscopy: Theory, Experiment, and Applications, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Samadani, E.; Farhad, S.; Scott, W.; Mastali, M.; Gimenez, L.E.; Fowler, M.; Fraser, R.A. Empirical Modeling of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy Tests. Electrochim. Acta 2015, 160, 169–177. [Google Scholar] [CrossRef]
- Boukamp, B.A. A Linear Kronig-Kramers Transform Test for Immittance Data Validation. J. Electrochem. Soc. 1995, 142, 1885–1894. [Google Scholar] [CrossRef]
- Stacy, A.; Gilaki, M.; Sahraei, E.; Soudbakhsh, D. Investigating the Effects of Mechanical Damage on Electrical Response of Li-ion Pouch Cells. In Proceedings of the 2020 American Control Conference, Denver, CO, USA, 1–3 July 2020; pp. 1715–1720. [Google Scholar]
- Derakhshan, M.; Gilaki, M.; Stacy, A.; Sahraei, E.; Soudbakhsh, D. Bending Detection of Li-Ion Pouch Cells Using Impedance Spectra. In Proceedings of the DSCC-Dynamic Systems & Control Conference 2020, Pittsburgh, PA, USA, 7–9 October 2020. to appear. [Google Scholar]
- Pastor-Fernández, C.; Uddin, K.; Chouchelamane, G.H.; Widanage, W.D.; Marco, J. A Comparison between Electrochemical Impedance Spectroscopy and Incremental Capacity-Differential Voltage as Li-Ion Diagnostic Techniques to Identify and Quantify the Effects of Degradation Modes within Battery Management Systems. J. Power Sources 2017, 360, 301–318. [Google Scholar] [CrossRef]
- Vector Network Analyzer-Bode 100. Available online: https://www.omicron-lab.com (accessed on 19 August 2020).








| Charge Procedure | Discharge Procedure | |
|---|---|---|
| Cycle 1–63 | CC charge at 750 mA | CC discharge at 750 mA |
| CV charge at 3.65 V | cut-off voltage: 2.5 V | |
| Cycle 64–89 | CC charge at 1500 mA | CC discharge at 1500 mA |
| CV charge at 3.65 V | cut-off voltage: 2.5 V |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soudbakhsh, D.; Gilaki, M.; Lynch, W.; Zhang, P.; Choi, T.; Sahraei, E. Electrical Response of Mechanically Damaged Lithium-Ion Batteries. Energies 2020, 13, 4284. https://doi.org/10.3390/en13174284
Soudbakhsh D, Gilaki M, Lynch W, Zhang P, Choi T, Sahraei E. Electrical Response of Mechanically Damaged Lithium-Ion Batteries. Energies. 2020; 13(17):4284. https://doi.org/10.3390/en13174284
Chicago/Turabian StyleSoudbakhsh, Damoon, Mehdi Gilaki, William Lynch, Peilin Zhang, Taeyoung Choi, and Elham Sahraei. 2020. "Electrical Response of Mechanically Damaged Lithium-Ion Batteries" Energies 13, no. 17: 4284. https://doi.org/10.3390/en13174284
APA StyleSoudbakhsh, D., Gilaki, M., Lynch, W., Zhang, P., Choi, T., & Sahraei, E. (2020). Electrical Response of Mechanically Damaged Lithium-Ion Batteries. Energies, 13(17), 4284. https://doi.org/10.3390/en13174284