Design Space Exploration of Turbulent Multiphase Flows Using Machine Learning-Based Surrogate Model
Abstract
:1. Introduction
2. Gaussian Process-Based Framework for Turbulent Multiphase Flows
2.1. Gaussian Process Regression for Fluid Flows
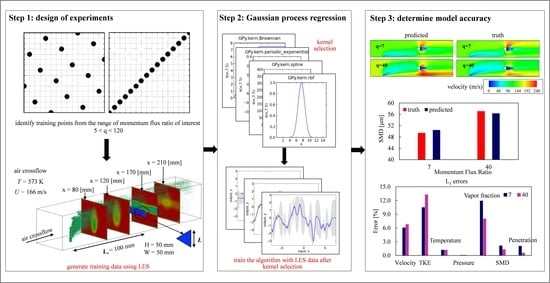
2.2. Framework
- Step 1: generation of training (and testing) data
- Step 2: Gaussian process regression
- Step 3: error quantification
3. Theoretical Formulations and Governing Equations for the Truth Model
3.1. Governing Equations for the Gaseous Phase
3.2. Dispersed Phase Modeling
3.2.1. Spray Closure Modeling
3.2.2. Coupling between Dispersed and Carrier Phase
4. Error Quantification and Speedup
5. Results and Discussion
5.1. Experimental Validation of the Truth Model
5.2. Configuration and Operating Conditions for Training Dataset
5.3. Results of Machine Emulation
5.3.1. Velocity Magnitude
5.3.2. Turbulent Kinetic Energy
5.3.3. Pressure and Temperature
5.3.4. Liquid-Vapor Fraction
5.3.5. Sauter Mean Diameter (SMD) and Jet Penetration Depth
5.4. Speedup
6. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, H.-G.; Khare, P.; Sung, H.-G.; Yang, V. A Large-Eddy-Simulation study of combustion dynamics of Bluff-Body stabilized flames. Combust. Sci. Technol. 2016, 188, 924–952. [Google Scholar] [CrossRef]
- Yoo, Y.-L.; Han, D.-H.; Hong, J.-S.; Sung, H.-G. A large eddy simulation of the breakup and atomization of a liquid jet into a cross turbulent flow at various spray conditions. Int. J. Heat Mass Transf. 2017, 112, 97–112. [Google Scholar] [CrossRef]
- Jiang, X.; Siamas, G.A.; Jagus, K.; Karayiannis, T.G. Physical modelling and advanced simulations of gas-liquid two-phase jet flows in atomization and sprays. Prog. Energy Combust. Sci. 2010, 36, 131–167. [Google Scholar] [CrossRef]
- Moin, P.; Apte, S.V. Large-eddy simulation of realistic gas turbine combustors. AIAA J. 2006, 44, 698–708. [Google Scholar] [CrossRef]
- Madabhushi, R.K. A Model for Numerical Simulation of Breakup of a Liquid Jet in Crossflow. At. Sprays 2003, 13, 413–424. [Google Scholar] [CrossRef]
- Erlebacher, G.; Hussaini, M.Y.; Speziale, C.G.; Zang, T.A. Toward the large-eddy simulations of compressible turbulent flows. J. Fluid Mech. 1992, 238, 155–185. [Google Scholar] [CrossRef] [Green Version]
- Broumand, M.; Birouk, M. Liquid jet in a subsonic gaseous crossflow: Recent progress and remaining challenges. Prog. Energy Combust. Sci. 2016, 57, 1–29. [Google Scholar] [CrossRef]
- Song, J.; Cain, C.C.; Lee, J.G. Liquid Jets in Subsonic Air Crossflow at Elevated Pressure. J. Eng. Gas Turbines Power 2014, 137. [Google Scholar] [CrossRef]
- Lee, K.; Aalburg, C.; Diez, F.J.; Faeth, G.M.; Sallam, K.A. Primary Breakup of Turbulent Round Liquid Jets in Uniform Crossflows. AIAA J. 2007, 45, 1907–1916. [Google Scholar] [CrossRef]
- Vich, G.; Ledoux, M. Investigation of a liquid jet in a subsonic cross-flow. Int. J. Fluid Mech. Res. 1997, 24, 1–12. [Google Scholar] [CrossRef]
- Kihm, K.D.; Lyn, G.M.; Son, S.Y. Atomization of Cross-Injecting Sprays Into Convective Air Stream. At. Sprays 1995, 5, 417–433. [Google Scholar] [CrossRef]
- Zang, Y.; Street, R.L.; Koseff, J.R. A dynamic mixed subgrid—Scale model and its application to turbulent recirculating flows. Phys. Fluids A Fluid Dyn. 1993, 5, 3186–3196. [Google Scholar] [CrossRef]
- Birouk, M.; Lekic, N. Liquid Jet Breakup in Quiescent Atmosphere: A Review. At. Sprays 2009, 19, 501–528. [Google Scholar] [CrossRef]
- Sallam, K.A.; Dai, Z.; Faeth, G.M. Liquid breakup at the surface of turbulent round liquid jets in still gases. Int. J. Multiph. Flow 2002, 28, 427–449. [Google Scholar] [CrossRef]
- Mazallon, J.; Dai, Z.; Faeth, G.M. Primary breakup of nonturbulent round liquid jets in gas crossflows. At. Sprays 1999, 9, 291–311. [Google Scholar] [CrossRef]
- Wu, P.-K.; Kirkendall, K.A.; Fuller, R.P.; Nejad, A.S. Breakup Processes of Liquid Jets in Subsonic Crossflows. J. Propuls. Power 1997, 13, 64–73. [Google Scholar] [CrossRef]
- Ganti, H.; Khare, P. Data-Driven Surrogate Modeling of Multiphase Flows Using Machine Learning Techniques. Comput. Fluids 2020, 211, 104626. [Google Scholar] [CrossRef]
- Wu, P.-K.; Faeth, G.M. Aerodynamic Effects on Primary Breakup of Turbulent Liquids. At. Sprays 1993, 3, 265–289. [Google Scholar] [CrossRef] [Green Version]
- Amighi, A.; Ashgriz, N. Global Droplet Size in Liquid Jet in a High-Temperature and High-Pressure Crossflow. AIAA J. 2019, 57, 1260–1274. [Google Scholar] [CrossRef]
- Oh, J.; Lee, J.G.; Lee, W. Vaporization of a liquid hexanes jet in cross flow. Int. J. Multiph. Flow 2013, 57, 151–158. [Google Scholar] [CrossRef]
- Stenzler, J.N.; Lee, J.G.; Santavicca, D.A.; Lee, W. Penetration of liquid jets in a cross-flow. At. Sprays 2006, 16, 887–906. [Google Scholar] [CrossRef]
- Rachner, M.; Julian, B.; Christoph, H.; Thomas, D. Modelling of the atomization of a plain liquid fuel jet in crossflow at gas turbine conditions. Aerosp. Sci. Technol. 2002, 6, 495–506. [Google Scholar] [CrossRef]
- Wang, Q.; Hesthaven, J.S.; Ray, D. Non-intrusive reduced order modeling of unsteady flows using artificial neural networks with application to a combustion problem. J. Comput. Phys. 2019, 384, 289–307. [Google Scholar] [CrossRef] [Green Version]
- Takbiri-Borujeni, A.; Kazemi, H.; Nasrabadi, N. A data-driven proxy to Stoke’s flow in porous media. arXiv 2019, arXiv:1905.06327. [Google Scholar]
- Yeh, S.-T.; Wang, X.; Sung, C.-L.; Mak, S.; Chang, Y.-H.; Zhang, L.; Wu, C.F.J.; Yang, V. Common Proper Orthogonal Decomposition-Based Spatiotemporal Emulator for Design Exploration. AIAA J. 2018, 56, 2429–2442. [Google Scholar] [CrossRef] [Green Version]
- Moiz, A.A.; Pal, P.; Probst, D.; Pei, Y.; Zhang, Y.; Som, S.; Kodavasal, J.A. A Machine Learning—Genetic Algorithm (ML-GA) Approach for Rapid Optimization Using High-Performance Computing. SAE Int. J. Commer. Veh. 2018, 11, 291–306. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part II): Data-driven Discovery of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Bai, Z.; Brunton, S.L.; Brunton, B.W.; Kutz, J.N.; Kaiser, E.; Spohn, A.; Noack, B.R. Data-Driven Methods in Fluid Dynamics: Sparse Classification from Experimental Data. In Whither Turbulence and Big Data in the 21st Century; Pollard, A., Castillo, L., Danaila, L., Glauser, M., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 323–342. [Google Scholar]
- Brunton, S.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [Green Version]
- Moonen, P.; Allegrini, J. Employing statistical model emulation as a surrogate for CFD. Environ. Model. Softw. 2015, 72, 77–91. [Google Scholar] [CrossRef]
- Bright, I.; Lin, G.; Kutz, J.N. Compressive sensing based machine learning strategy for characterizing the flow around a cylinder with limited pressure measurements. Phys. Fluids 2013, 25. [Google Scholar] [CrossRef]
- Kamin, M.; Khare, P. Liquid jet in crossflow: Effect of momentum flux ratio on spray and vaporization characteristics. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Khare, P.; Wang, S.; Yang, V. Modeling of finite-size droplets and particles in multiphase flows. Chin. J. Aeronaut. 2015, 28, 974–982. [Google Scholar] [CrossRef] [Green Version]
- Hadfield, S.; Lawrence, N.D.; Wilkinson, R.; Durrande, N. Gaussian Process Summer School. 2017. Available online: http://gpss.cc/gpss17/ (accessed on 2 September 2020).
- Ebden, M. Gaussian processes: A quick introduction. arXiv 2015, arXiv:1505.02965. [Google Scholar]
- Rasmussen, C.E. Gaussian Processes in Machine Learning; Springer: Berlin/Heidelberg, Germany, 2004; pp. 63–71. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Wang, B. How priors of initial hyperparameters affect Gaussian process regression models. Neurocomputing 2018, 275, 1702–1710. [Google Scholar] [CrossRef] [Green Version]
- GPSS. GPy: A Gaussian Process Framework in Python. 2014. Available online: http://github.com/SheffieldML/GPy (accessed on 2 September 2020).
- Viana, F.A.C. A Tutorial on Latin Hypercube Design of Experiments. Qual. Reliab. Eng. Int. 2016, 32, 1975–1985. [Google Scholar] [CrossRef]
- Shields, M.D.; Zhang, J. The generalization of Latin hypercube sampling. Reliab. Eng. Syst. Saf. 2016, 148, 96–108. [Google Scholar] [CrossRef] [Green Version]
- Oefelein, J.C.; Yang, V. Modeling High-Pressure Mixing and Combustion Processes in Liquid Rocket Engines. J. Propuls. Power 1998, 14, 843–857. [Google Scholar] [CrossRef]
- Reitz, R. Modeling atomization processes in high-pressure vaporizing sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Liu, A.B.; Mather, D.; Reitz, R.D. Modeling the effects of drop drag and breakup on fuel sprays. SAE Trans. 1993, 102, 83–95. [Google Scholar]
- O’Rourke, P.J.; Amsden, A.A. The TAB Method for Numerical Calculation of Spray Droplet Breakup. SAE Technical Paper 872089. 1987. Available online: https://www.sae.org/publications/technical-papers/content/872089/ (accessed on 10 August 2020). [CrossRef] [Green Version]
- Mundo, C.; Sommerfeld, M.; Tropea, C. Droplet-wall collisions: Experimental studies of the deformation and breakup process. Int. J. Multiph. Flow 1995, 21, 151–173. [Google Scholar] [CrossRef]
















| Non-Vaporizing Case | Vaporization Case | |
|---|---|---|
| Ta (K) | 300 | 600 |
| Ua (m/s) | 116 | 166 |
| Uj (m/s) | 12.01 | 12.3 |
| ρa (kg/m3) | 1.18 | 0.62 |
| σo (N/m) | 7.28 × 10−2 | 7.28 × 10−2 |
| µa (Ns/m2) | 1.86 × 10−5 | 2.98 × 10−5 |
| q | 9 | 9 |
| We | 68 | 68 |
| Re | 2059.3 | 933.7 |
| Training Dataset Identified by the Momentum Flux Ratio, q | ||||||
|---|---|---|---|---|---|---|
| 5 | 8 | 10 | 30 | 50 | 100 | 120 |
| Testing Dataset Identified by the Momentum Flux Ratio, q | ||||||
|---|---|---|---|---|---|---|
| 7 | 9 | 20 | 40 | 65 | 90 | 110 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ganti, H.; Kamin, M.; Khare, P. Design Space Exploration of Turbulent Multiphase Flows Using Machine Learning-Based Surrogate Model. Energies 2020, 13, 4565. https://doi.org/10.3390/en13174565
Ganti H, Kamin M, Khare P. Design Space Exploration of Turbulent Multiphase Flows Using Machine Learning-Based Surrogate Model. Energies. 2020; 13(17):4565. https://doi.org/10.3390/en13174565
Chicago/Turabian StyleGanti, Himakar, Manu Kamin, and Prashant Khare. 2020. "Design Space Exploration of Turbulent Multiphase Flows Using Machine Learning-Based Surrogate Model" Energies 13, no. 17: 4565. https://doi.org/10.3390/en13174565
APA StyleGanti, H., Kamin, M., & Khare, P. (2020). Design Space Exploration of Turbulent Multiphase Flows Using Machine Learning-Based Surrogate Model. Energies, 13(17), 4565. https://doi.org/10.3390/en13174565