Dynamic Pore-Scale Network Modeling of Spontaneous Water Imbibition in Shale and Tight Reservoirs
Abstract
:1. Introduction
2. Dynamic Pore Network Modelling of Water Imbibition
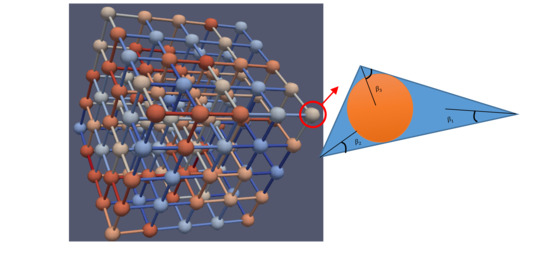
2.1. Pore Network Generation
2.2. Control Equations and Conductance Calculation
2.3. Local Capillary Pressure Function
2.4. Solution Scheme and Boundary Conditions
3. Dynamic Pore-Scale Network Modeling of Water Imbibition in Shale and Tight Formations
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Cross-area of a pore element | |
| Local capillary pressure function coefficient | |
| Coefficient accounting extra resistance of wetting layers | |
| Coefficient of piston-like displacement | |
| Coefficient of snap-off | |
| Shape factor of cross-area | |
| Corner shape factor | |
| Absolute conductance of a pore element | |
| Relative conductance of a pore element | |
| Water saturation | |
| Capillary pressure | |
| The characteristic length of imbibition | |
| The perimeter of the cross-area of a pore element | |
| Pore body volume | |
| Phase pressure | |
| Pore or throat radius | |
| Half angle of the corners | |
| Contact angle | |
| Fluid viscosity | |
| Interfacial tension | |
| Porosity | |
| Time step size | |
| Dimensionless time for imbibition upscaling | |
| Superscript | |
| Non-wetting phase | |
| Wetting phase | |
| Current time step | |
| Next time step | |
| Subscript | |
| th pore element | |
| th pore element | |
| Connecting throat between th and th pore elements | |
References
- Shanley, K.W.; Cluff, R.M.; Robinson, J.W. Factors controlling prolific gas production from low-permeability sandstone reservoirs: Implications for resource assessment, prospect development, and risk analysis. AAPG Bull. 2004, 88, 1083–1121. [Google Scholar] [CrossRef] [Green Version]
- Shaoul, J.R.; van Zelm, L.F.; De Pater, C.J. Damage mechanisms in unconventional-gas-well Stimulation--a new look at an old problem. SPE Prod. Oper. 2011, 26, 388–400. [Google Scholar]
- Hirasaki, G.; Zhang, D.L. Surface chemistry of oil recovery from fractured, oil-wet, carbonate formations. SPE J. 2004, 9, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Austad, T. Wettability and oil recovery from carbonates: Effects of temperature and potential determining ions. Colloids Surf. A Physicochem. Eng. Asp. 2006, 279, 179–187. [Google Scholar] [CrossRef]
- Sheng, J.J. Review of surfactant enhanced oil recovery in carbonate reservoirs. Adv. Pet. Explor. Dev. 2013, 6, 1–10. [Google Scholar]
- Wang, D.; Butler, R.; Zhang, J.; Seright, R. Wettability survey in Bakken shale with surfactant-formulation imbibition. SPE Reserv. Eval. Eng. 2012, 15, 695–705. [Google Scholar] [CrossRef]
- Alvarez, J.O.; Schechter, D.S. Wettability alteration and spontaneous imbibition in unconventional liquid reservoirs by surfactant additives. SPE Reserv. Eval. Eng. 2017, 20, 10117. [Google Scholar] [CrossRef]
- Sheng, J.J. What type of surfactants should be used to enhance spontaneous imbibition in shale and tight reservoirs? J. Pet. Sci. Eng. 2017, 159, 635–643. [Google Scholar] [CrossRef]
- Zhang, X.; Morrow, N.R.; Ma, S. Experimental verification of a modified scaling group for spontaneous imbibition. SPE Reserv. Eng. 1996, 11, 280–285. [Google Scholar] [CrossRef]
- Akin, S.; Schembre, J.M.; Bhat, S.K.; Kovscek, A.R. Spontaneous imbibition characteristics of diatomite. J. Pet. Sci. Eng. 2000, 25, 149–165. [Google Scholar] [CrossRef]
- Zhou, X.; Morrow, N.R.; Ma, S. Interrelationship of wettability, initial water saturation, aging time, and oil recovery by spontaneous imbibition and waterflooding. SPE J. 2000, 5, 199–207. [Google Scholar] [CrossRef]
- Morrow, N.R.; Mason, G. Recovery of oil by spontaneous imbibition. Curr. Opin. Colloid Interface Sci. 2001, 6, 321–337. [Google Scholar] [CrossRef]
- Fischer, H.; Morrow, N.R. Scaling of oil recovery by spontaneous imbibition for wide variation in aqueous phase viscosity with glycerol as the viscosifying agent. J. Pet. Sci. Eng. 2006, 52, 35–53. [Google Scholar] [CrossRef]
- Takahashi, S.; Kovscek, A.R. Spontaneous countercurrent imbibition and forced displacement characteristics of low-permeability, siliceous shale rocks. J. Pet. Sci. Eng. 2010, 71, 47–55. [Google Scholar] [CrossRef]
- Roychaudhuri, B.; Tsotsis, T.T.; Jessen, K. An experimental investigation of spontaneous imbibition in gas shales. J. Pet. Sci. Eng. 2013, 111, 87–97. [Google Scholar] [CrossRef]
- Morsy, S.; Sheng, J.J. Imbibition characteristics of the barnett shale formation. In Proceedings of the SPE Unconventional Resources Conference, The Woodlands, TX, USA, 1–3 April 2014. SPE-168984-MS. [Google Scholar]
- Lucas, R. Rate of capillary ascension of liquids. Kolloid Z 1918, 23, 15–22. [Google Scholar] [CrossRef]
- Li, K.; Horne, R. Characterization of Spontaneous Water Imbibition into Gas-Saturated Rocks. In Proceedings of the SPE/AAPG Western Regional Meeting, Long Beach, CA, USA, 19–22 June 2000. [Google Scholar]
- Cai, J.; Perfect, E.; Cheng, C.L.; Hu, X. Generalized modeling of spontaneous imbibition based on Hagen–Poiseuille flow in tortuous capillaries with variably shaped apertures. Langmuir 2014, 30, 5142–5151. [Google Scholar] [CrossRef]
- Mason, G.; Morrow, N.R. Developments in spontaneous imbibition and possibilities for future work. J. Pet. Sci. Eng. 2013, 110, 268–293. [Google Scholar] [CrossRef]
- Øren, P.E.; Bakke, S.; Arntzen, O.J. Extending predictive capabilities to network models. SPE J. 1998, 3, 324–336. [Google Scholar] [CrossRef]
- Valvatne, P.H.; Blunt, M.J. Predictive pore-scale modeling of two-phase flow in mixed wet media. Water Resour. Res. 2004, 40, W07406. [Google Scholar] [CrossRef] [Green Version]
- Behbahani, H.; Blunt, M.J. Analysis of imbibition in mixed-wet rocks using pore-scale modeling. SPE J. 2005, 10, 466–474. [Google Scholar] [CrossRef] [Green Version]
- Behbahani, H.S.; Di Donato, G.; Blunt, M.J. Simulation of counter-current imbibition in water-wet fractured reservoirs. J. Pet. Sci. Eng. 2006, 50, 21–39. [Google Scholar] [CrossRef]
- Wang, X.; Sheng, J.J. Spontaneous imbibition analysis in shale reservoirs based on pore network modeling. J. Pet. Sci. Eng. 2018, 169, 663–672. [Google Scholar] [CrossRef]
- Wang, X.; Sheng, J.J. A self-similar analytical solution of spontaneous and forced imbibition in porous media. Adv. Geo-Energ. Res. 2018, 2, 260–268. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.H.; Sheppard, A.P.; Knackstedt, M.A.; Pinczewski, W.V. The effect of displacement rate on imbibition relative permeability and residual saturation. J. Pet. Sci. Eng. 2006, 52, 54–70. [Google Scholar] [CrossRef]
- Blunt, M.J. Multiphase Flow in Permeable Media: A Pore-Scale Perspective; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Sheng, Q.; Thompson, K. A unified pore-network algorithm for dynamic two-phase flow. Adv. Water Resour. 2016, 95, 92–108. [Google Scholar] [CrossRef]
- Blunt, M.J.; Scher, H. Pore-level modeling of wetting. Phys. Rev. E 1995, 52, 6387. [Google Scholar] [CrossRef]
- Hughes, R.G.; Blunt, M.J. Pore scale modeling of rate effects in imbibition. Transp. Porous Media 2000, 40, 295–322. [Google Scholar] [CrossRef]
- Idowu, N.A.; Blunt, M.J. Pore-scale modelling of rate effects in waterflooding. Transp. Porous Media 2010, 83, 151–169. [Google Scholar] [CrossRef]
- Aghaei, A.; Piri, M. Direct pore-to-core up-scaling of displacement processes: Dynamic pore network modeling and experimentation. J. Hydrol. 2015, 522, 488–509. [Google Scholar] [CrossRef] [Green Version]
- Aker, E.; Måløy, K.J.; Hansen, A.; Batrouni, G.G. A two-dimensional network simulator for two-phase flow in porous media. Transp. Porous Media 1998, 32, 163–186. [Google Scholar] [CrossRef]
- Al-Gharbi, M.S.; Blunt, M.J. Dynamic network modeling of two-phase drainage in porous media. Phys. Rev. E 2005, 71, 016308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tørå, G.; Øren, P.E.; Hansen, A. A dynamic network model for two-phase flow in porous media. Transp. Porous Media 2012, 92, 145–164. [Google Scholar] [CrossRef]
- Khayrat, K. Modeling Hysteresis for Two-Phase Flow in Porous Media: From Micro to Macro Scale. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2016. [Google Scholar]
- Joekar-Niasar, V.; Hassanizadeh, S.M.; Dahle, H.K. Non-equilibrium effects in capillarity and interfacial area in two-phase flow: Dynamic pore-network modelling. J. Fluid Mech. 2010, 655, 38–71. [Google Scholar] [CrossRef]
- Khayrat, K.; Jenny, P. A multi-scale network method for two-phase flow in porous media. J. Comput. Phys. 2017, 342, 194–210. [Google Scholar] [CrossRef]
- Mason, G.; Morrow, N.R. Capillary behavior of a perfectly wetting liquid in irregular triangular tubes. J. Colloid Interface Sci. 1991, 141, 262–274. [Google Scholar] [CrossRef]
- Ransohoff, T.C.; Radke, C.J. Laminar flow of a wetting liquid along the corners of a predominantly gas-occupied noncircular pore. J. Colloid Interface Sci. 1988, 121, 392–401. [Google Scholar] [CrossRef]
- Bakke, S.; Øren, P.E. 3-D pore-scale modeling of sandstones and flow simulations in the pore networks. SPE J. 1997, 2, 136–149. [Google Scholar] [CrossRef] [Green Version]
- Patzek, T.W. Verification of a complete pore network simulator of drainage and imbibition. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 3–5 April 2000. [Google Scholar]
- Andersen, P.Ø.; Skjæveland, S.M.; Standnes, D.C. A Novel Bounded Capillary Pressure Correlation with Application to Both Mixed and Strongly Wetted Porous Media. In Proceedings of the SPE Abu Dhabi International Petroleum Exhibition & Conference, 13–16 November 2017. SPE-188291-MS. [Google Scholar]
- Aziz, K.; Settari, A. Petroleum Reservoir Simulation; Chapman & Hall: London, UK, 1979. [Google Scholar]
- Moghaddam, R.N.; Jamiolahmady, M. Fluid transport in shale gas reservoirs: Simultaneous effects of stress and slippage on matrix permeability. Int. J. Coal Geol. 2016, 163, 87–99. [Google Scholar] [CrossRef]
- Wang, X.; Sheng, J.J. Pore network modeling of the non-Darcy flows in shale and tight formations. J. Pet. Sci. Eng. 2018, 163, 511–518. [Google Scholar] [CrossRef]
- Morrow, N.R. The effects of surface roughness on contact: Angle with special reference to petroleum recovery. J. Can. Pet. Technol. 1975, 14, 42–53. [Google Scholar] [CrossRef] [Green Version]
- Ma, S.; Zhang, X.; Morrow, N.R. Influence of fluid viscosity on mass transfer between rock matrix and fractures. J. Can. Pet. Technol. 1999, 38, 25–30. [Google Scholar] [CrossRef]















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Sheng, J.J. Dynamic Pore-Scale Network Modeling of Spontaneous Water Imbibition in Shale and Tight Reservoirs. Energies 2020, 13, 4709. https://doi.org/10.3390/en13184709
Wang X, Sheng JJ. Dynamic Pore-Scale Network Modeling of Spontaneous Water Imbibition in Shale and Tight Reservoirs. Energies. 2020; 13(18):4709. https://doi.org/10.3390/en13184709
Chicago/Turabian StyleWang, Xiukun, and James J. Sheng. 2020. "Dynamic Pore-Scale Network Modeling of Spontaneous Water Imbibition in Shale and Tight Reservoirs" Energies 13, no. 18: 4709. https://doi.org/10.3390/en13184709
APA StyleWang, X., & Sheng, J. J. (2020). Dynamic Pore-Scale Network Modeling of Spontaneous Water Imbibition in Shale and Tight Reservoirs. Energies, 13(18), 4709. https://doi.org/10.3390/en13184709