Faraday’s Efficiency Modeling of a Proton Exchange Membrane Electrolyzer Based on Experimental Data
Abstract
:1. Introduction
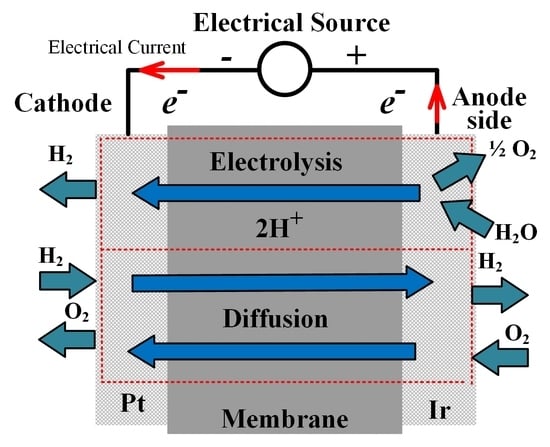
2. Research Background
3. Study of the Faraday’s Efficiency
3.1. Description of the Experimental Test Bench
3.2. Analysis of the Faraday’s Efficiency Based on the Cathode Gas Pressure Change
3.3. Mathematical Modeling of the Faraday’s Efficiency
3.4. Validation of the Developed Models
4. Discussion and Future Challenges
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PEM | proton exchange membrane |
| SO | solid oxide |
Nomenclature
| Hydrogen flow rate (mol.s−1 or slpm) | |
| ηel | energy efficiency |
| ηF | Faraday’s efficiency |
| nc | Number of the electrolyzer cells |
| iel | Electrolyzer current (A) |
| z | Number of electrons exchanged during the reaction |
| F | Faraday’s constant (F = 96485 C.mol−1) |
| ηv | Cell voltage efficiency |
| ΔH | Hydrogen higher heating value (ΔH = 286,000 Joule) |
| vel | Stack voltage (V) |
| vcell | Cell voltage (V) |
| VH2 | Hydrogen volume (m3) |
| ηel | Electrolyzer efficiency |
| t | Total time the constant current has been applied (s) |
| p | Ambient pressure (Pa) |
| R | Universal gas constant (R = 8.314 J. mol−1. K−1) |
| T | Ambient temperature (K) |
References
- Buttler, A.; Spliethoff, H. Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: A review. Renew. Sustain. Energy Rev. 2018, 82, 2440–2454. [Google Scholar] [CrossRef]
- Carmo, M.; Stolten, D. Energy Storage Using Hydrogen Produced From Excess Renewable Electricity. In Science and Engineering of Hydrogen-Based Energy Technologies; Elsevier: Amsterdam, The Netherlands, 2019; pp. 165–199. [Google Scholar]
- Wulf, C.; Linssen, J.; Zapp, P. Power-to-Gas—Concepts, Demonstration, and Prospects. In Hydrogen Supply Chains; Elsevier: Amsterdam, The Netherlands, 2018; pp. 309–345. [Google Scholar]
- Hiva Kumar, S.; Himabindu, V. Hydrogen production by PEM water electrolysis—A review. Mater. Sci. Energy Technol. 2019, 2, 442–454. [Google Scholar] [CrossRef]
- Carmo, M.; Fritz, D.L.; Mergel, J.; Stolten, D. A comprehensive review on PEM water electrolysis. Int. J. Hydrog. Energy 2013, 38, 4901–4934. [Google Scholar] [CrossRef]
- Falcão, D.; Pinto, A. A review on PEM electrolyzer modelling: Guidelines for beginners. J. Clean. Prod. 2020, 261, 121184. [Google Scholar] [CrossRef]
- David, M.; Ocampo-Martínez, C.; Sánchez-Peña, R. Advances in alkaline water electrolyzers: A review. J. Energy Storage 2019, 23, 392–403. [Google Scholar] [CrossRef] [Green Version]
- Nikolaidis, P.; Poullikkas, A. A comparative overview of hydrogen production processes. Renew. Sustain. Energy Rev. 2017, 67, 597–611. [Google Scholar] [CrossRef]
- Brauns, J.; Turek, T. Alkaline Water Electrolysis Powered by Renewable Energy: A Review. Processes 2020, 8, 248. [Google Scholar] [CrossRef] [Green Version]
- Ulleberg, Øystein Modeling of advanced alkaline electrolyzers: A system simulation approach. Int. J. Hydrog. Energy 2003, 28, 21–33. [CrossRef]
- Jupudi, R.S.; Zappi, G.; Bourgeois, R. Prediction of shunt currents in a bipolar electrolyzer stack by difference calculus. J. Appl. Electrochem. 2007, 37, 921–931. [Google Scholar] [CrossRef]
- Colli, A.; Girault, H.H. Compact and General Strategy for Solving Current and Potential Distribution in Electrochemical Cells Composed of Massive Monopolar and Bipolar Electrodes. J. Electrochem. Soc. 2017, 164, E3465–E3472. [Google Scholar] [CrossRef] [Green Version]
- Tang, A.; McCann, J.; Bao, J.; Skyllas-Kazacos, M. Investigation of the effect of shunt current on battery efficiency and stack temperature in vanadium redox flow battery. J. Power Sources 2013, 242, 349–356. [Google Scholar] [CrossRef]
- Kim, S. Vanadium Redox Flow Batteries: Electrochemical Engineering. Energy Storage Devices 2019. [Google Scholar] [CrossRef]
- Hug, W.; Bussmann, H.; Brinner, A. Intermittent operation and operation modeling of an alkaline electrolyzer. Int. J. Hydrog. Energy 1993, 18, 973–977. [Google Scholar] [CrossRef]
- Ulleberg, O. Stand-Alone Power Systems for the Future: Optimal Design, Operation and Control of Solar-Hydrogen Energy Systems. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 1998. [Google Scholar]
- Tijani, A.S.; Rahim, A.A. Numerical Modeling the Effect of Operating Variables on Faraday Efficiency in PEM Electrolyzer. Procedia Technol. 2016, 26, 419–427. [Google Scholar] [CrossRef] [Green Version]
- Ben Makhloufi, A.; Hatti, M.; Taleb, R. Comparative Study of Photovoltaic System for Hydrogen Electrolyzer System. In Proceedings of the 6th International Conference on Systems and Control (ICSC), Batna, Algeria, 7–9 May 2017. [Google Scholar]
- Tlili, N.; Neily, B.; Ben Salem, F. Modeling and Simulation of Hybrid System Coupling a Photovoltaic Generator, A PEM Fuel Cell and An Electrolyzer (Part I). In Proceedings of the IEEE 11th International Multi-Conference on Systems, Signals & Devices (SSD14), Barcelona, Spain, 11–14 February 2014. [Google Scholar]
- Ganguly, A.; Misra, D.; Ghosh, S. Modeling and analysis of solar photovoltaic-electrolyzer-fuel cell hybrid power system integrated with a floriculture greenhouse. Energy Build. 2010, 42, 2036–2043. [Google Scholar] [CrossRef]
- Li, C.-H.; Zhu, X.-J.; Cao, G.-Y.; Sui, S.; Hu, M. Dynamic modeling and sizing optimization of stand-alone photovoltaic power systems using hybrid energy storage technology. Renew. Energy 2009, 34, 815–826. [Google Scholar] [CrossRef]
- Sarrias-Mena, R.; Ramírez, L.M.F.; García-Vázquez, C.A.; Jurado, F.; Sarrias-Mena, R. Electrolyzer models for hydrogen production from wind energy systems. Int. J. Hydrog. Energy 2015, 40, 2927–2938. [Google Scholar] [CrossRef]
- Ribeiro, E.; Cardoso, A.; Boccaletti, C. Power Converters Analysis in a Renewable Energy Based Hybrid System with Hydrogen Storage. In Proceedings of the IET Conference on Renewable Power Generation (RPG 2011), Edinburgh, UK, 6–8 September 2011. [Google Scholar]
- Onar, O.C.; Uzunoglu, M.; Alam, M.S. Dynamic modeling, design and simulation of a wind/fuel cell/ultra-capacitor-based hybrid power generation system. J. Power Sources 2006, 161, 707–722. [Google Scholar] [CrossRef]
- Tjarks, G.; Stolten, D.; Lanzerath, F.; Müller, M.; Bardow, A.; Stolten, D. Energetically-optimal PEM electrolyzer pressure in power-to-gas plants. Appl. Energy 2018, 218, 192–198. [Google Scholar] [CrossRef]
- Khalilnejad, A.; Sundararajan, A.; Sarwat, A.I. Optimal design of hybrid wind/photovoltaic electrolyzer for maximum hydrogen production using imperialist competitive algorithm. J. Mod. Power Syst. Clean Energy 2018, 6, 40–49. [Google Scholar] [CrossRef] [Green Version]
- Tijani, A.S.; Yusup, N.A.B.; Rahim, A.A. Mathematical Modelling and Simulation Analysis of Advanced Alkaline Electrolyzer System for Hydrogen Production. Procedia Technol. 2014, 15, 798–806. [Google Scholar] [CrossRef] [Green Version]
- Zhou, T.; François, B. Modeling and control design of hydrogen production process for an active hydrogen/wind hybrid power system. Int. J. Hydrog. Energy 2009, 34, 21–30. [Google Scholar] [CrossRef]
- Schalenbach, M.; Carmo, M.; Fritz, D.L.; Mergel, J.; Stolten, D. Pressurized PEM water electrolysis: Efficiency and gas crossover. Int. J. Hydrog. Energy 2013, 38, 14921–14933. [Google Scholar] [CrossRef]
- Liso, V.; Savoia, G.; Araya, S.S.; Cinti, G.; Kær, S.K. Modelling and Experimental Analysis of a Polymer Electrolyte Membrane Water Electrolysis Cell at Different Operating Temperatures. Energies 2018, 11, 3273. [Google Scholar] [CrossRef] [Green Version]
- Scheepers, F.; Stähler, M.; Stähler, A.; Rauls, E.; Müller, M.; Carmo, M.; Lehnert, W. Improving the Efficiency of PEM Electrolyzers through Membrane-Specific Pressure Optimization. Energies 2020, 13, 612. [Google Scholar] [CrossRef] [Green Version]
- Yodwong, B.; Guilbert, D.; Kaewmanee, W.; Phattanasak, M. Energy Efficiency Based Control Strategy of a Three-Level Interleaved DC-DC Buck Converter Supplying a Proton Exchange Membrane Electrolyzer. Electronics 2019, 8, 933. [Google Scholar] [CrossRef] [Green Version]
- Guilbert, D.; Vitale, G. Improved Hydrogen-Production-Based Power Management Control of a Wind Turbine Conversion System Coupled with Multistack Proton Exchange Membrane Electrolyzers. Energies 2020, 13, 1239. [Google Scholar] [CrossRef] [Green Version]
- Colli, A.; Bisang, J.M. Combination of Cumulative and Convergent Flows as a Means to Improve the Uniformity of Tertiary Current Distribution in Parallel-Plate Electrochemical Reactors. J. Electrochem. Soc. 2017, 164, E42–E47. [Google Scholar] [CrossRef]
- Colli, A.; Bisang, J. The effect of a perpendicular and cumulative inlet flow on the mass-transfer distribution in parallel-plate electrochemical reactors. Electrochim. Acta 2014, 137, 758–776. [Google Scholar] [CrossRef]
- Colli, A.; Bisang, J.M. Validation of Theory with Experiments for Local Mass Transfer at Parallel Plate Electrodes under Laminar Flow Conditions. J. Electrochem. Soc. 2012, 160, E5–E11. [Google Scholar] [CrossRef]







| Parameters | Value | Unit |
|---|---|---|
| Rated electrical power | 400 | W |
| Stack operating voltage range | 4.4–8 | V |
| Stack current range | 0–50 | A |
| Delivery output pressure | 0.1–10.5 | bar |
| Cells number | 3 | - |
| Active area Section | 50 | cm2 |
| Membrane thickness | 25.4 | µm |
| 1 Bar. | 5 Bar. | 10 Bar. | |||||||
|---|---|---|---|---|---|---|---|---|---|
| iel (A) | VH2exp | VH2th | ηF | VH2exp | VH2th | ηF | VH2exp | VH2th | ηF |
| 1 | 0.0226 | 0.0227 | 0.9949 | 0.0044 | 0.0045 | 0.9814 | 0.0022 | 0.0023 | 0.9644 |
| 3 | 0.0681 | 0.0682 | 0.9983 | 0.0136 | 0.0136 | 0.9938 | 0.0067 | 0.0068 | 0.9881 |
| 5 | 0.1136 | 0.1137 | 0.9990 | 0.0226 | 0.0227 | 0.9963 | 0.0113 | 0.0114 | 0.9929 |
| 7 | 0.1590 | 0.1591 | 0.9993 | 0.0317 | 0.0318 | 0.9973 | 0.0158 | 0.0159 | 0.9949 |
| 10 | 0.2272 | 0.2273 | 0.9995 | 0.0454 | 0.0455 | 0.9981 | 0.0227 | 0.0227 | 0.9964 |
| 20 | 0.4546 | 0.4547 | 0.9997 | 0.0909 | 0.0909 | 0.9991 | 0.0454 | 0.0455 | 0.9982 |
| 30 | 0.6819 | 0.6820 | 0.9998 | 0.1363 | 0.1364 | 0.9994 | 0.0681 | 0.0682 | 0.9988 |
| 40 | 0.9093 | 0.9094 | 0.9999 | 0.1818 | 0.1819 | 0.9995 | 0.0909 | 0.0909 | 0.9991 |
| 50 | 1.1366 | 1.1367 | 0.9999 | 0.2273 | 0.2273 | 0.9996 | 0.1136 | 0.1137 | 0.9993 |
| p (Bar) | a | b | c |
|---|---|---|---|
| 1 | −0.005103 | −1 | 1 |
| 5 | −0.01871 | −1 | 1 |
| 10 | −0.03572 | −1 | 1 |
| a1 | a2 |
|---|---|
| −0.0034 | −0.001711 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yodwong, B.; Guilbert, D.; Phattanasak, M.; Kaewmanee, W.; Hinaje, M.; Vitale, G. Faraday’s Efficiency Modeling of a Proton Exchange Membrane Electrolyzer Based on Experimental Data. Energies 2020, 13, 4792. https://doi.org/10.3390/en13184792
Yodwong B, Guilbert D, Phattanasak M, Kaewmanee W, Hinaje M, Vitale G. Faraday’s Efficiency Modeling of a Proton Exchange Membrane Electrolyzer Based on Experimental Data. Energies. 2020; 13(18):4792. https://doi.org/10.3390/en13184792
Chicago/Turabian StyleYodwong, Burin, Damien Guilbert, Matheepot Phattanasak, Wattana Kaewmanee, Melika Hinaje, and Gianpaolo Vitale. 2020. "Faraday’s Efficiency Modeling of a Proton Exchange Membrane Electrolyzer Based on Experimental Data" Energies 13, no. 18: 4792. https://doi.org/10.3390/en13184792
APA StyleYodwong, B., Guilbert, D., Phattanasak, M., Kaewmanee, W., Hinaje, M., & Vitale, G. (2020). Faraday’s Efficiency Modeling of a Proton Exchange Membrane Electrolyzer Based on Experimental Data. Energies, 13(18), 4792. https://doi.org/10.3390/en13184792