Energy-Based Vibration Modeling and Solution of High-Speed Elevators Considering the Multi-Direction Coupling Property
Abstract
:1. Introduction
2. Structural and Vibrational Characteristics
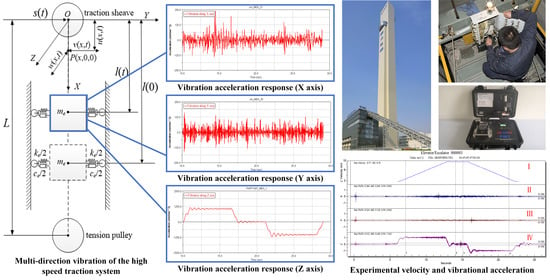
2.1. Basic Structure of a High-Speed Traction System
2.2. Analysis of Multi-Direction Coupling Vibration
- Radial deformation scale could be neglected compared with axial stretch. Small elements on the traction rope share the same scalar of velocity, and physical parameters (such as elasticity modulus, linear density) are generally constant.
- The guide rail and the elevator well do not belong to the traction system. Fabrication uncertainties, installation deviation of the guide rail, and airflow of the elevator well are not the direct causes of traction system vibration, which could be simplified as constant perturbations at the contact point between the traction sheave and the rope.
- The traction sheave and the tension pulley are treated as mass points considering the significant dimensional difference between the length of the traction rope and the radius of pulleys. Therefore, the segmented strings are connected at the mass centers of the traction sheave and the tension pulley.
3. Vibration Modeling Based on Energy Methods
3.1. Formulations of the Vibration Model Based on Energy Analysis
3.2. Basic Energy-Based Vibration Model (EVM)
3.3. EVM with External Perturbations
4. Solution of EVM
4.1. Discretization of the Vibration Model
4.2. Solution of the Discretized EVM
4.2.1. Solving EVM through Gaussian Precise Integration
4.2.2. Computation of the physical property index matrix (PPIM)
5. Case Study
5.1. Operating Parameters of the Example Elevator
5.2. Operating State Equation of the Example Elevator
5.3. EVM of KLK2 High-Speed Elevator
5.4. Solution of the Established EVM
5.5. Comparison and Verification between Vibration Models
6. Conclusions
- The characteristics of the traction system is analyzed and simulated using masses, springs and dampers. A combination of kinematic energy, elastic potential energy and virtual work provides a description of the multi-direction coupling vibration properties, based on which EVM method is established.
- EVM contains a complicated partial differential equation set with unlimited degrees of freedom and time-varying parameters. This paper discretizes the EVM to an ordinary differential equation set through the time-varying element method, and obtain the solutions using the Gaussian precise integration method.
- An example study is conducted using KLK2 high-speed elevator. EVM is then established to obtain the simulation results and the solutions of vibrational acceleration indices, and A95, along X, Y, Z axis. The obtained results are then compared with the conventional DVM method and experimental data of KLK2 prototype. The proposed EVM method could achieve more accurate results than the conventional DVM method, and deviations of these indicators are less than 5%. In this way, efficiency, potential and reliability of the proposed EVM method have been elaborated and verified.
Author Contributions
Funding
Conflicts of Interest
Data Availability Statement
References
- Fung, R.F.; Lin, J.H.; Yao, C.M. Vibration analysis and suppression control of an elevator string actuated by a PM synchronous servo motor. J. Sound Vib. 1997, 206, 399–423. [Google Scholar] [CrossRef]
- Peng, Q.; Jiang, A.; Yuan, H.; Huang, G.; He, S.; Li, S. Study on Theoretical Model and Test Method of Vertical Vibration of Elevator Traction System. Math. Probl. Eng. 2020, 2020. [Google Scholar] [CrossRef] [Green Version]
- Crespo, R.S.; Kaczmarczyk, S.; Picton, P.; Su, H. Modelling and simulation of a stationary high-rise elevator system to predict the dynamic interactions between its components. Int. J. Mech. Sci. 2018, 137, 24–45. [Google Scholar] [CrossRef]
- Kaczmarczyk, S.; Andrew, J.P.; Adams, J.P. The Modelling and Prediction of the Influence of Building Vibration on the Dynamic Response of Elevator Ropes. Mater. Sci. Forum 2003, 440–441, 489–496. [Google Scholar] [CrossRef]
- Yang, D.H.; Kim, K.Y.; Kwak, M.K.; Lee, S. Dynamic modeling and experiments on the coupled vibrations of building and elevator ropes. J. Sound Vib. 2017, 390, 164–191. [Google Scholar] [CrossRef]
- Kobayashi, S.; Yoshimura, T.; Noguchi, N.; Omiya, A. Estimation of dynamic characteristics of an elevator car using operational modal analysis. Nihon Kikai Gakkai Ronbunshu C Hen/Trans. Jpn. Soc. Mech. Eng. Part C 2008, 74, 548–553. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Wang, C.; Zhang, Q. Response analysis of the composite random vibration of a high-speed elevator considering the nonlinearity of guide shoe. J. Braz. Soc. Mech. Sci. Eng. 2018, 40. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, C.; Zhang, Q.; Liu, J. Response analysis of non-linear compound random vibration of a high-speed elevator. J. Mech. Sci. Technol. 2019, 33, 51–63. [Google Scholar] [CrossRef]
- Wee, H.; Kim, Y.Y.; Jung, H.; Lee, G.N. Nonlinear rate-dependent stick-slip phenomena: Modeling and parameter estimation. Int. J. Solids Struct. 2001, 38, 1415–1431. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Q.; Zhang, R.; Zhang, L. Transverse Vibration Response of a Super High-Speed Elevator under Air Disturbance. Int. J. Struct. Stab. Dyn. 2019, 19, 1950103. [Google Scholar] [CrossRef]
- Taplak, H.; Erkaya, S.; Yildirim, Ş.; Uzmay, I. The Use of Neural Network Predictors for Analyzing the Elevator Vibrations. Arab. J. Sci. Eng. 2014, 39, 1157–1170. [Google Scholar] [CrossRef]
- Utsunomiya, K.; Okamoto, K.I.; Yumura, T.; Funai, K.; Kuraoka, H. Active roller guide system for high-speed elevators. Elev. World 2002, 50, 198–205. [Google Scholar]
- Mirabdollah Yani, R.; Ghodsi, R.; Darabi, E. A closed-form solution for nonlinear oscillation and stability analyses of the elevator cable in a drum drive elevator system experiencing free vibration. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4467–4484. [Google Scholar] [CrossRef]
- Teshima, N.; Kamimura, K.; Nagai, M.; Kou, S.; Kamada, T. Vibration Control of Ultra High Speed Elevator by Active Mass Damper: 1st Report, Study by Optimal Control Theory. Nihon Kikai Gakkai Ronbunshu, C Hen/Trans. Jpn. Soc. Mech. Eng. Part C 1999, 65, 3479–3485. [Google Scholar] [CrossRef]
- Gaiko, N.V.; van Horssen, W.T. Resonances and vibrations in an elevator cable system due to boundary sway. J. Sound Vib. 2018, 424, 272–292. [Google Scholar] [CrossRef]
- Otsuki, M.; Ushijima, Y.; Yoshida, K.; Kimura, H.; Nakagawa, T. Application of nonstationary sliding mode control to suppression of transverse vibration of elevator rope using input device with gaps. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2006, 49, 385–394. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, Y.; Tomisawa, M.; Okada, K.; Sugiyama, Y. Vibration control of super-high-speed elevators: (Car vibration control method based on computer simulation and experiment using a full-size car model). JSME Int. J. Ser. C Dyn. Control Robot. Des. Manuf. 1997, 40, 74–81. [Google Scholar] [CrossRef]
- Kimura, H.; Nakagawa, T. Vibration analysis of elevator rope with vibration suppressor. Nihon Kikai Gakkai Ronbunshu C Hen/Trans. Jpn. Soc. Mech. Eng. Part C 2005, 71, 442–447. [Google Scholar] [CrossRef]
- Arrasate, X.; Kaczmarczyk, S.; Almandoz, G.; Abete, J.M.; Isasa, I. The modelling, simulation and experimental testing of the dynamic responses of an elevator system. Mech. Syst. Signal Process. 2014, 42, 258–282. [Google Scholar] [CrossRef]
- Santo, D.R.; Balthazar, J.M.; Tusset, A.M.; Piccirilo, V.; Brasil, R.M.L.R.F.; Silveira, M. On nonlinear horizontal dynamics and vibrations control for high-speed elevators. JVC J. Vib. Control 2018, 24, 825–838. [Google Scholar] [CrossRef]
- Nakano, K.; Hayashi, R.; Suda, Y.; Noguchi, N.; Arakawa, A. Active Vibration Control of an Elevator Car Using Two Rotary Actuators. J. Syst. Des. Dyn. 2011, 5, 155–163. [Google Scholar] [CrossRef]
- Noguchi, N.; Arakawa, A.; Miyoshi, K.; Kawamura, Y.; Yoshimura, T. Active vibration control technology for elevator cars considering controllability. Nihon Kikai Gakkai Ronbunshu C Hen/Trans. Jpn. Soc. Mech. Eng. Part C 2013, 79, 3192–3205. [Google Scholar] [CrossRef] [Green Version]
- Noguchi, N.; Arakawa, A.; Miyata, K.; Yoshimura, T.; Shin, S. Study on Active Vibration Control for High-Speed Elevators. J. Syst. Des. Dyn. 2011, 5, 164–179. [Google Scholar] [CrossRef]
- Utsunomiya, K.; Okamoto, K.; Yumura, T.; Sakuma, Y. Vibration control of high-speed elevators taking account of electricity consumption reduction. Nihon Kikai Gakkai Ronbunshu C Hen/Trans. Jpn. Soc. Mech. Eng. Part C 2006, 72, 2048–2055. [Google Scholar] [CrossRef]
- Utsunomiya, K. Vibration Damping Device for an Elevator. J. Acoust. Soc. Am. 2011, 129, 3419. [Google Scholar] [CrossRef]
- Baek, K.-H.; Kim, K.-Y.; Kwak, M.-K. Dynamic Modeling and Controller Design for Active Control of High-speed Elevator Front-back Vibrations. Trans. Korean Soc. Noise Vib. Eng. 2011, 21, 74–80. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.Y.; Park, M.R.; Sim, J.H.; Hong, J.P. Advanced Method of Selecting Number of Poles and Slots for Low-Frequency Vibration Reduction of Traction Motor for Elevator. IEEE/ASME Trans. Mechatron. 2017, 22, 1554–1562. [Google Scholar] [CrossRef]
- Kang, J.K.; Sul, S.K. Vertical-vibration control of elevator using estimated car acceleration feedback compensation. IEEE Trans. Ind. Electron. 2000, 47, 91–99. [Google Scholar] [CrossRef]
- Nguyen, T.X.; Miura, N.; Sone, A. Analysis and control of vibration of ropes in a high-rise elevator under earthquake excitation. Earthq. Eng. Eng. Vib. 2019, 18, 447–460. [Google Scholar] [CrossRef]
- Dos Santos, L.C.C.; Brasil, R.M.L.R.F.; Balthazar, J.M.; Piccirillo, V.; Tusset, A.M.; Santo, D.R. Active vibration control of an elevator system using magnetorheological damper actuator. Int. J. Nonlinear Dyn. Control 2017, 1, 114. [Google Scholar] [CrossRef]
- Fan, W.; Zhu, W.D. Dynamic analysis of an elevator traveling cable using a singularity-free beam formulation. In Proceedings of the ASME Design Engineering Technical Conference, Cleveland, OH, USA, 6–9 August 2017; Volume 6. [Google Scholar]
- Rijanto, E.; Muramatsu, T.; Tagawa, Y. Control of elevator having parametric vibration using LPV control method: Simulation study in the case of constant vertical velocity. In Proceedings of the IEEE Conference on Control Applications, Kohala Coast, HI, USA, 22–27 August 1999. [Google Scholar]
- Mutoh, N.; Kagomiya, K.; Kurosawa, T.; Konya, M.; Andoh, T. Horizontal Vibration Suppression Method Suitable for Super-High-Speed Elevators. IEEJ Trans. Ind. Appl. 1998, 118, 353–362. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Zhang, J.; Zhao, Y. Modeling and robust control of horizontal vibrations for high-speed elevator. JVC/J. Vib. Control 2009, 15, 1375–1396. [Google Scholar] [CrossRef]
- Zhang, P.; Bao, J.H.; Zhu, C.M. Dynamic analysis of hoisting viscous damping string with time-varying length. J. Phys. Conf. Ser. 2013, 448. [Google Scholar] [CrossRef]
- Kimura, H.; Ito, H.; Fujita, Y.; Nakagawa, T. Forced vibration analysis of an elevator rope with both ends moving. J. Vib. Acoust. Trans. ASME 2007, 129, 471–477. [Google Scholar] [CrossRef]
- Lu, Y. Dynamics of the Flexble Multibody Syestems; Higher Education Press: Beijing, China, 1996. [Google Scholar]
- Irgens, F. Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-74298-2. [Google Scholar]
- Wan-Xie, Z. On precise integration method. J. Comput. Appl. Math. 2004. [Google Scholar] [CrossRef] [Green Version]
- ISO 18738-1:2012, Lifts (Elevators)-Measurement of Ride Quality[S]. 2012. Available online: https://www.iso.org/standard/54395.html (accessed on 7 July 2020).
- Shabana, A.A. Dynamics of Multibody Systems, 2nd ed.; Cambridge University Press: Cambridge, UK, 1998; ISBN 13: 978-0521594462. [Google Scholar]
- The World’s Standard of Measurement Elevator Ride Quality, Vibration & Sound. Available online: https://www.pmtvib.com/eva-625 (accessed on 7 July 2020).










| Phase | Time Used | Description |
|---|---|---|
| 1 | Acceleration increases to | |
| 2 | Acceleration remains constant. | |
| 3 | Acceleration reduces to . Velocity increases to . | |
| 4 | Velocity remains constant. | |
| 5 | Deacceleration decreases to | |
| 6 | Deacceleration remains constant. | |
| 7 | Deacceleration increases to . Velocity increases to . |
| DVM Method | EVM Method | Prototype Experiments | ||
|---|---|---|---|---|
| X axis | 0.363 | 0.376 | 0.384 | |
| Y axis | 0.305 | 0.317 | 0.324 | |
| Z axis | 0.495 | 0.503 | 0.512 | |
| A95 | X axis | 0.245 | 0.251 | 0.264 |
| Y axis | 0.114 | 0.118 | 0.120 | |
| Z axis | 0.417 | 0.429 | 0.440 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, L.; He, C.; Yi, G.; Zhang, S.; Wang, Y.; Rao, Y.; Zhang, L. Energy-Based Vibration Modeling and Solution of High-Speed Elevators Considering the Multi-Direction Coupling Property. Energies 2020, 13, 4821. https://doi.org/10.3390/en13184821
Qiu L, He C, Yi G, Zhang S, Wang Y, Rao Y, Zhang L. Energy-Based Vibration Modeling and Solution of High-Speed Elevators Considering the Multi-Direction Coupling Property. Energies. 2020; 13(18):4821. https://doi.org/10.3390/en13184821
Chicago/Turabian StyleQiu, Lemiao, Ci He, Guodong Yi, Shuyou Zhang, Yang Wang, Yong Rao, and Lichun Zhang. 2020. "Energy-Based Vibration Modeling and Solution of High-Speed Elevators Considering the Multi-Direction Coupling Property" Energies 13, no. 18: 4821. https://doi.org/10.3390/en13184821
APA StyleQiu, L., He, C., Yi, G., Zhang, S., Wang, Y., Rao, Y., & Zhang, L. (2020). Energy-Based Vibration Modeling and Solution of High-Speed Elevators Considering the Multi-Direction Coupling Property. Energies, 13(18), 4821. https://doi.org/10.3390/en13184821