Distributed Economic Dispatch Scheme for Droop-Based Autonomous DC Microgrid
Abstract
:1. Introduction
- Decentralized economic dispatch scheme that requires local information only. This type of optimal control is less expensive because no communication is needed. However, the lack of common information (such as the common bus voltage in DC MG) leads to the challenge in utilizing all available resources in the network. Additionally, the power and voltage oscillation may happen, if every DGs regulate their output power just taking their own generation costs into account.
- Distributed economic dispatch scheme that requires only local computation and information exchange among some neighboring units through a sparse communication network. Based on the well-designed distributed schemes, the EDP can be solved by multiple distributed controllers working in parallel, which increases the reliability, flexibility, and scalability of the system. Therefore, the distributed manners are considered as promising options for the optimal control and management of microgrid. However, there are also many problems remained to be solved before the distributed schemes become more practical for microgrid, such as time delay, the capability of plug and play, the choice of communication topology, and so on.
- The proposed distributed scheme can resolve the problems of power sharing accuracy and voltage oscillation caused by the estimation errors, which cannot be effectively solved by decentralized methods.
- The economical regulator updates the control signal with the newest information in each iteration step, instead of requiring the achievement of consensus. Therefore, the convergence speed of the proposed scheme is faster than the traditional consensus-based economic dispatch scheme, which is important for large-scale system.
- To support the flexible operation of DGs, the proposed scheme also adds the capability of plug and play into cyber layer to promote the reliability and scalability of the distributed scheme.
- The impact of time delay on the voltage estimation is analyzed in detail, and the capability of inhibiting oscillation caused by time delay is used to optimize the topology of the sparse communication network.
2. Preliminaries
2.1. Problem Formation of EDP
2.2. Discrete Consensus Algorithm
3. Proposed Distributed Economic Dispatch Scheme
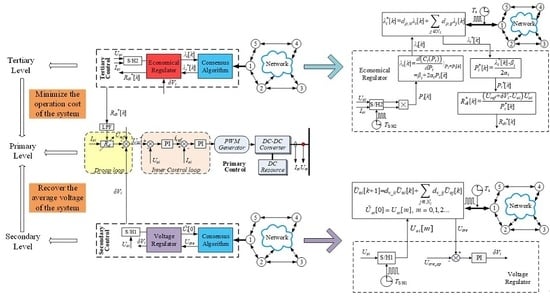
3.1. Primary Control
3.2. Voltage Regulation in Secondary Control
3.3. Economical Regulation in Tertiary Control
3.4. The Consideration of Power Limitation
3.5. The Global Dynamic Model and Parameter Design
4. The Performance of Voltage Estimation and Topology Optimization
4.1. The Impact of Time Delay on Average Voltage Estimation
4.2. Network Topology Optimization
- The Determination of Gf: The total number of network with n nodes is NG = 2[(n − 1)n]/2. The Warshall algorithm is used to judge the connectivity of the NG topologies, which is necessary for consensus algorithm. Then, all connective graphics are classified according to the node degree, and the heterogeneous graphics are selected to form the Gf.
- The Solution of Multi-objective Optimization Model: Searching for the Pareto frontier of multi-objective optimization model (41) subject to the discrete domain Gf determined by (1) based on non-dominated sorting method. At last, the optimal network topology will be selected from the frontier by evaluation function.
5. Case Study Based on the Proposed Scheme
5.1. Simulation Configuration
5.2. Simulation Results
5.2.1. Case 1: Performance of the Scheme with Changing Load
5.2.2. Case 2: The Comparison of Control Scheme in Different Levels
5.2.3. Case 3: The Comparison between the Proposed Scheme and the Mathematical Programming Method
5.2.4. Case 4: Performance of the Scheme Considering Generation Limitation
5.2.5. Case 5: Plug and Play Capability of the Scheme
5.2.6. Case 6: Performance of Optimal Topology
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lasseter, R.H. Smart distribution: Coupled microgrids. Proc. IEEE 2011, 99, 1074–1082. [Google Scholar] [CrossRef]
- Lou, G.; Gu, W.; Wang, W.; Song, X.; Gao, F. Distributed model predictive secondary voltage control of islanded microgrids with feedback linearization. IEEE Access 2018, 6, 50169–50178. [Google Scholar] [CrossRef]
- Anand, S.; Fernandes, B.G.; Guerrero, J. Distributed control to ensure proportional load sharing and improve voltage regulation in low-voltage dc microgrids. IEEE Trans. Power Electron. 2013, 28, 1900–1913. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Lu, X.; Yang, X.; Wang, W.; Xu, D. An improved distributed secondary control method for dc microgrids with enhanced dynamic current sharing performance. IEEE Trans. Power Electron. 2016, 31, 6658–6673. [Google Scholar] [CrossRef]
- Nutkani, I.U.; Loh, P.C.; Blaabjerg, F. Droop scheme with consideration of operating costs. IEEE Trans. Power Electron. 2014, 29, 1047–1052. [Google Scholar] [CrossRef]
- Abido, M.A. Optimal design of power-system stabilizers using particle swarm optimization. IEEE Trans. Energy Convers. 2002, 17, 406–413. [Google Scholar] [CrossRef]
- Linda, M.M.; Nair, N.K. Optimal design of multi-machine power system stabilizer using robust ant colony optimization technique. IEEE Trans. Instrum. Meas. Control 2012, 34, 829–840. [Google Scholar] [CrossRef]
- Meng, L.; Dragicevic, T.; Guerrero, J.M. Stability constrained efficiency optimization for droop-controlled DC-DC conversion system. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 7222–7227. [Google Scholar]
- Yazdanian, M.; Mehrizi-Sani, A. Distributed control techniques in microgrids. IEEE Trans. Smart Grid 2014, 5, 2901–2909. [Google Scholar] [CrossRef]
- Nutkani, I.U.; Loh, P.C.; Wang, P.; Blaabjerg, F. Cost-prioritized droop schemes for autonomous ac microgrids. IEEE Trans. Power Electron. 2015, 30, 1109–1119. [Google Scholar] [CrossRef]
- Nutkani, I.U.; Wang, P.; Loh, P.C.; Blaabjerg, F. Autonomous economic operation of grid connected DC microgrid. In Proceedings of the IEEE 5th International Symposium on PEDG, Galway, Ireland, 24–27 June 2014; pp. 1–5. [Google Scholar]
- Nutkani, I.U.; Wang, P.; Loh, P.C.; Blaabjerg, F. Cost-based droop scheme for DC microgrid. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 765–769. [Google Scholar]
- Xin, H.; Zhao, R.; Zhang, L.; Wang, Z.; Wong, K.P.; Wei, W. A decentralized hierarchical control structure and self-optimizing control strategy for F-P type DGs in islanded microgrids. IEEE Trans. Smart Grid 2016, 7, 3–5. [Google Scholar] [CrossRef]
- Chen, F.; Chen, M.; Li, Q.; Meng, K.; Zheng, Y.; Guerrero, J. Cost-based droop schemes for economic dispatch in islanded microgrids. IEEE Trans. Smart Grid 2017, 8, 63–74. [Google Scholar] [CrossRef] [Green Version]
- Nutkani, I.U.; Loh, P.C.; Wang, P.; Blaabjerg, F. Linear decentralized power sharing schemes for economic operation of AC microgrids. IEEE Trans. Ind. Electron. 2016, 63, 225–234. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, W. Novel Multiagent Based Load Restoration Algorithm for Microgrids. IEEE Trans. Smart Grid 2011, 2, 152–161. [Google Scholar] [CrossRef]
- Li, P.; Zhang, C.; Wu, Z.; Xu, Y.; Hu, M.; Dong, Z. Distributed adaptive robust voltage/var control with network partition in active distribution networks. IEEE Trans. Smart Grid 2019, in press. [Google Scholar] [CrossRef]
- Nasirian, V.; Moayedi, S.; Davoudi, A.; Lewis, F.L. Distributed cooperative control of dc microgrids. IEEE Trans. Power Electron. 2015, 30, 2288–2303. [Google Scholar] [CrossRef]
- Nasirian, V.; Davoudi, A.; Lewis, F.L.; Guerrero, J.M. Distributed adaptive droop control for DC distribution systems. IEEE Trans. Energy Convers. 2014, 29, 944–956. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Zhang, W.; Liu, W. Distributed dynamic programming-based approach for economic dispatch in smart grids. IEEE Trans. Ind. Inform. 2015, 11, 166–175. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, W.; Zhang, B. A fully distributed power dispatch method for fast frequency recovery and minimal generation cost in autonomous microgrids. IEEE Trans. Smart Grid 2016, 7, 19–31. [Google Scholar] [CrossRef]
- Binetti, G.; Davoudi, A.; Naso, D.; Turchiano, B.; Lewis, F.L. A distributed auction-based algorithm for the nonconvex economic dispatch problem. IEEE Trans. Ind. Inform. 2014, 10, 1124–1132. [Google Scholar] [CrossRef]
- Zhang, Z.; Chow, M.Y. Convergence analysis of the incremental cost consensus algorithm under different communication network topologies in a smart grid. IEEE Trans. Power Syst. 2012, 27, 1761–1768. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, Y.; Liu, W.; Zhang, C.; Yu, H. Distributed online optimal energy management for smart grids. IEEE Trans. Ind. Inform. 2015, 11, 717–727. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, W.; Hug, G.; Kar, S.; Li, Z. Cooperative control of distributed energy storage system in a microgrid. IEEE Trans. Smart Grid 2015, 6, 238–248. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z. Distributed optimal resource management based on the consensus algorithm in a microgrid. IEEE Trans. Ind. Electron. 2015, 62, 2584–2592. [Google Scholar] [CrossRef]
- Rahbari-Asr, N.; Ojha, U.; Zhang, Z.; Chow, M.Y. Incremental welfare consensus algorithm for cooperative distributed generation/demand response in smart grid. IEEE Trans. Smart Grid 2014, 5, 2836–2845. [Google Scholar] [CrossRef]
- Hu, J.; Duan, J.; Ma, H.; Chow, M.Y. Distributed adaptive droop control for optimal power dispatch in dc microgrid. IEEE Trans. Ind. Electron. 2018, 65, 778–789. [Google Scholar] [CrossRef]
- Moayedi, S.; Davoudi, A. Unifying distributed dynamic optimization and control of islanded DC microgrids. IEEE Trans. Power Electron. 2017, 32, 2329–2346. [Google Scholar] [CrossRef]
- Das, D.B.; Patvardhan, C. New multi-objective stochastic search technique for economic load dispatch. IEE Proc. Gener. Transm. Distrib. 1998, 145, 747–752. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Xiao, F.; Wang, L.; Wang, A. Consensus problems in discrete-time multiagent systems with fixed topology. J. Math. Anal. Appl. 2006, 322, 587–598. [Google Scholar] [CrossRef] [Green Version]
- Franklin, G.F.; Workman, M.L.; Powell, D. Digital Control of Dynamic System, 2rd ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1990. [Google Scholar]
- Wang, L.; Xiao, F. A new approach to consensus problems in discrete-time multiagent systems with time-delays. Sci. China Ser. F Inf. Sci. 2007, 50, 625–635. [Google Scholar] [CrossRef]
- Braitor, A.; Mills, A.R.; Kadirkamanathan, V.; Konstantopoulos, G.C.; Norman, P.G.; Jones, C.E. Control of DC power distribution system of a hybrid electric aircraft with inherent overcurrent protection. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference, Nottingham, UK, 7–9 November 2018; pp. 1–6. [Google Scholar]
- Cupelli, L.; Schumacher, M.; Monti, A.; Mueller, D.; De Tommasi, L.; Kouramas, K. Simulation Tools and Optimization Algorithms for Efficient Energy Management in Neighborhoods. In Energy Positive Neighborhoods and Smart Energy Districts; Elsevier: Amsterdam, The Netherlands, 2017; pp. 57–100. [Google Scholar]




















| System | α ($/kW2h) | β ($/kWh) | γ ($/h) |
|---|---|---|---|
| PV + BA | 0.01 | 0.1 | 0.0015 |
| MT1 | 0.018 | 0.19 | 0.05 |
| FC1 | 0.011 | 0.15 | 0.015 |
| MT2 | 0.02 | 0.2 | 0.04 |
| FC2 | 0.01 | 0.14 | 0.01 |
| Parameters | Unit | Values |
|---|---|---|
| Nominal dc voltage | V | 500 |
| System reference voltage | V | 505 |
| Filter inductance | mH | 5 |
| DC capacitance | uF | 1600 |
| Initial virtual resistance | Ω | 1.2 |
| Switch frequency | kHz | 10 |
| Load 2, 3, 4, 5 | kW | 5 |
| Load 1 | kW | 10 |
| Line resistance | Ω | 0.4 |
| Maximum output | kW | 15 |
| kp | ki | N | Ts (ms) | Tm (ms) | Uave_op (V) |
|---|---|---|---|---|---|
| 0.3 | 15 | 11 | 2 | 6 | 500 |
| Parameters | Mathematical Programming | The Proposed Scheme | ||||
|---|---|---|---|---|---|---|
| 0.15–0.4 s | 0.4–0.7 s | 0.7–1 s | 0.15–0.4 s | 0.4–0.7 s | 0.7–1 s | |
| P1 (kW) | 10.0 | 11.29 | 12.45 | 10.20 | 11.50 | 12.75 |
| P2 (kW) | 3.10 | 3.82 | 4.42 | 3.16 | 3.87 | 4.58 |
| P3 (kW) | 6.83 | 8.0 | 9.05 | 7.0 | 8.15 | 9.32 |
| P4 (kW) | 2.55 | 3.2 | 3.73 | 2.60 | 3.23 | 3.88 |
| P5 (kW) | 8.0 | 9.3 | 10.45 | 8.18 | 9.45 | 10.74 |
| Uo1 (V) | 501.1 | 500.7 | 501.5 | 500.5 | 499.4 | 500.0 |
| Uo2 (V) | 496.4 | 496.5 | 498.1 | 498.80 | 498.2 | 499.4 |
| Uo3 (V) | 500.9 | 502.3 | 501.3 | 500.25 | 500.91 | 499.5 |
| Uo4 (V) | 498.9 | 500.84 | 500.0 | 498.20 | 499.41 | 498.5 |
| Uo5 (V) | 502.5 | 503.6 | 503.9 | 501.9 | 502.2 | 502.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Z.; Wu, Z.; Dou, X.; Zhou, M.; Hu, W. Distributed Economic Dispatch Scheme for Droop-Based Autonomous DC Microgrid. Energies 2020, 13, 404. https://doi.org/10.3390/en13020404
Lv Z, Wu Z, Dou X, Zhou M, Hu W. Distributed Economic Dispatch Scheme for Droop-Based Autonomous DC Microgrid. Energies. 2020; 13(2):404. https://doi.org/10.3390/en13020404
Chicago/Turabian StyleLv, Zhenyu, Zaijun Wu, Xiaobo Dou, Min Zhou, and Wenqiang Hu. 2020. "Distributed Economic Dispatch Scheme for Droop-Based Autonomous DC Microgrid" Energies 13, no. 2: 404. https://doi.org/10.3390/en13020404
APA StyleLv, Z., Wu, Z., Dou, X., Zhou, M., & Hu, W. (2020). Distributed Economic Dispatch Scheme for Droop-Based Autonomous DC Microgrid. Energies, 13(2), 404. https://doi.org/10.3390/en13020404