An Analytical Model for Production Analysis of Hydraulically Fractured Shale Gas Reservoirs Considering Irregular Stimulated Regions
Abstract
:1. Introduction
2. Method
- The reservoir is homogeneous, isopachous and isothermal in each region.
- Flow process is 1-D linear in each region.
- Flow is single gas phase.
- The high-velocity non-Darcy flow in the hydraulic fracture is considered.
- The bottom-hole pressure is constant.
- The impact of gravity is neglected.
- Gas desorption meets the Langmuir isotherm adsorption equation.
2.1. Gas Adsorption/Desorption Effect
2.2. High-Velocity Non-Darcy Flow Effect
2.3. Non-Darcy Flow in the Matrix
2.4. Derivation of Linearized Gas Diffusivity Equation.
2.5. Model Description in Different Regions.
2.5.1. Model Description in Matrix Region (Region 2)
2.5.2. Model Description in Stimulated Region Volume (Region 1)
2.5.3. Model Description in Hydraulic Fracture Region
3. Results
3.1. Derivation of Analytical Solution.
3.2. Model Validation with Numerical Models
3.3. Irregular Stimulated Region with One Hydraulic Fracture
3.4. Irregular Stimulated Regions with Several Hydraulic Fractures
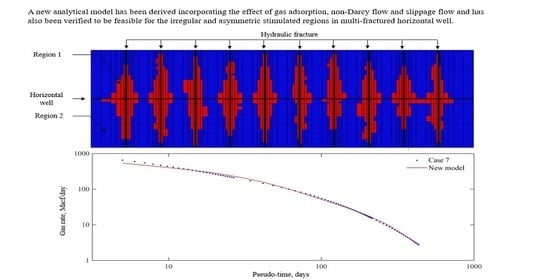
3.5. Application to Field Case
- Apply the given parameters and gas material balance equation to transform the time into pseudo-time and pressure into pseudo-pressure.
- Make a diagnostic plot of production rate vs. pseudo-time.
- Analyze the diagnostic plot to identify flow regimes.
- Fit Equation (75) to the production data to obtain the model parameters τF, τ1, τ2, Tr21/Tr1F, Tr1F/J, and qiF.
- Output the model parameters until a satisfactory matching is obtained.
- Following the step-by-step procedure to calculate the volume of hydraulic fracture region, region 1, and region 2.
- Make forecast of production rate with the model parameters.
4. Discussion
5. Conclusions
- A simple rate versus pseudo-time relationship is presented to account for transient linear and boundary-dominated flow periods in shale gas formation.
- Incorporating the effect of gas adsorption, non-Darcy flow, and slippage flow in the analytical model by defining the modified pseudo-pressure and pseudo-time, accuracy is improved in production forecast in shale gas reservoir.
- Comparing to the Laplace-transform solution, our analytical model is derived in real-time space and it is unnecessary to undertake dimensionless transformation and numerical inversion. It is more applicable in field scale.
- Through the model parameters obtained from history matching the field data, the production rate and cumulative production can be forecasted. In addition, the pore volume of different regions can also be calculated by step-by-step procedure, which was validated to be feasible for the irregular and asymmetric stimulated regions in multifractured horizontal wells. According to the results, the calculation accuracy is less than 10% and meets the engineering requirements.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| the volume of the adsorbed gas, ft3 | |
| the reservoir pressure, Psi | |
| Langmuir volume | |
| Langmuir pressure | |
| rock compressibility, Psi−1 | |
| water compressibility, Psi−1 | |
| free gas compressibility, Psi−1 | |
| adsorbed gas compressibility, Psi−1 | |
| total compressibility, Psi−1 | |
| modified total compressibility, Psi−1 | |
| gas reservoir volume factor | |
| modified compressibility factor | |
| compressibility factor | |
| standard compressibility factor | |
| reservoir temperature, K | |
| standard condition temperature, K | |
| standard condition pressure, Psi | |
| average reservoir pressure, Psi | |
| hydraulic fracture permeability, mD | |
| equivalent hydraulic fracture permeability, mD | |
| matrix permeability, mD | |
| intrinsic permeability, mD | |
| region 1 permeability, mD | |
| region 2 permeability, mD | |
| pore radius, ft | |
| the universal gas constant | |
| the gas molecular weight | |
| Knudsen number | |
| volume of the region | |
| pore volume of the region | |
| initial production rate from the hydraulic fracture region | |
| initial production rate from region 1 | |
| initial production rate from region 2 | |
| production time, days | |
| pseudo-time, days | |
| pseudo-time in fracture region, days | |
| pseudo-time in region 1, days | |
| pseudo-time in region 2, days | |
| approximate pseudo-time, days | |
| pseudo-pressure in region 2 | |
| pseudo-pressure in region 1 | |
| pseudo-pressure in hydraulic region | |
| average pseudo-pressure in region 2 | |
| average pseudo-pressure in region 1 | |
| average pseudo-pressure in fracture region | |
| half-width of hydraulic fracture, ft | |
| region 1 impact distance, ft | |
| half distance between fractures, ft | |
| half-length of macro-fracture, ft | |
| depth of top reservoir, ft | |
| depth of bottom reservoir, ft | |
| region 1 constant time, days | |
| region 2 constant time, days | |
| hydraulic region constant time, days | |
| transmissibility between region 1 and region 2, STB/D/psi | |
| transmissibility between microfracture and matrix, STB/D/psi | |
| hydraulic fracture region production index, STB/D/psi | |
| pore volumes of hydraulic region | |
| pore volumes of region 1 | |
| pore volumes of region 2 | |
| correlation parameter | |
| non-Darcy flow coefficient | |
| porosity | |
| matrix density, g/cm3 | |
| fluid viscosity, cp | |
| gas flow velocity |
Appendix A. Derivation of the Average Pseudo-Pressure
Appendix B. Solution of the System of ODEs
References
- Hu, X.Y.; Li, M.T.; Peng, C.G.; Davarpanah, A. Hybrid Thermal-Chemical Enhanced Oil Recovery Methods—An Experimental Study for Tight Reservoirs. Symmetry 2020, 12, 947. [Google Scholar] [CrossRef]
- Jin, Y.; Davarpanah, A. Using Photo-Fenton and Floatation Techniques for the Sustainable Management of Flow-Back Produced Water Reuse in Shale Reservoirs Exploration. Water Air Soil Pollut. 2020, 231, 1–8. [Google Scholar] [CrossRef]
- Hu, X.; Xie, J.; Cai, W.; Wang, R.; Davarpanah, A. Thermodynamic Effects of Cycling Carbon Dioxide Injectivity in Shale Reservoirs. J. Pet. Sci. Eng. 2020, 195, 107717. [Google Scholar] [CrossRef]
- Wu, M.L.; Ding, M.C.; Yao, J.; Li, C.; Huang, Z.; Xu, S. Production-Performance Analysis of Composite Shale-Gas reservoirs by the Boundary-Element Method. SPE Reserv. Eval. Eng. 2019, 22, 238–252. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.H.; Zhou, M.H.; Lu, W.; Davarpanah, A. Application of Symmetry Law in Numerical Modeling of Hydraulic Fracturing by Finite Element Method. Symmetry 2020, 12, 1122. [Google Scholar] [CrossRef]
- Sun, H.; Chawathe, A.; Hoteit, H.; Shi, X.; Li, L. Understanding Shale Gas Flow Behavior Using Numerical Simulation. SPE J. 2015, 20, 142–154. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, Q.; Ayala, L.F. Semi-Analytical Modeling of Multi-Mechanism Gas Transport in Shale Reservoirs with Complex Hydraulic-Fracture Geometries by the Boundary Element Method. In Proceedings of the SPE Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September–2 October 2019. SPE Paper 195902-MS. [Google Scholar]
- Davarpanah, A.; Shirmohammadi, R.; Mirshekari, B.; Aslani, A. Analysis of hydraulic fracturing techniques: Hybrid fuzzy approaches. Arab. J. Geosci. 2019, 12, 402. [Google Scholar] [CrossRef]
- Nobakht, M.; Clarkson, C.R. A New Analytical Method for Analyzing Linear Flow in Tight/Shale Gas Reservoirs: Constant-Flowing-Pressure Boundary Condition. SPE Reserv. Eval. Eng. 2012, 15, 370–384. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.L.; Zhang, L.H.; Luo, J.X.; Zhang, B.-N. Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir. J. Hydrol. 2014, 512, 447–456. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Qanbari, F. An Approximate Semianalytical Multiphase Forecasting Method for Multifractured Tight Light-Oil Wells With Complex Fracture Geometry. J. Can. Pet. Technol. 2015, 54, 489–508. [Google Scholar] [CrossRef]
- Wei, S.M.; Xia, Y.; Jin, Y. Quantitative study in shale gas behaviors using a coupled triple-continuum and discrete fracture model. J. Pet. Sci. Eng. 2019, 174, 49–69. [Google Scholar] [CrossRef]
- Wang, Q.; Wan, J.F.; Mu, L.F.; Shen, R.; Jurado, M.J.; Ye, Y. An Analytical Solution for Transient Productivity Prediction of Multi-Fractured Horizontal Wells in Tight Gas Reservoirs Considering Nonlinear Porous Flow Mechanisms. Energies 2020, 13, 1066. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Jiang, S.; Wu, X.Y. Development and Calibration of a Semianalytic Model for Shale Wells with Nonuniform Distribution of Induced Fractures Based on ES-MDA Method. Energies 2020, 13, 3718. [Google Scholar] [CrossRef]
- Lee, S.T.; Brockenbrough, J. A New Analytic Solution for Finite Conductivity Vertical Fractures With Real Time and Laplace Space Parameter Estimation. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Francisco, CA, USA, 5–8 October 1983. SPE Paper 12013-MS. [Google Scholar]
- Wattenbarger, R.A.; El-Banbi, A.H.; Villegas, M.E.; Maggard, J.B. Production Analysis of Linear Flow into Fractured Tight Gas Wells. In Proceedings of the SPE Rocky Mountain Regional/Low-Permeability Reservoirs Symposium, Denver, CO, USA, 5–8 April 1998. SPE Paper 39931-MS. [Google Scholar]
- El-Banbi, A.H.; Wattenbarger, R.A. Analysis of Linear Flow in Gas Well Production. In Proceedings of the SPE Gas Technology Symposium, Calgary, AB, Canada, 15–18 March 1998. SPE Paper 39972-MS. [Google Scholar]
- Bello, R.O.; Wattenbarger, R.A. Multi-Stage Hydraulically Fractured Horizontal Shale Gas Well Rate Transient Analysis. In Proceedings of the North Africa Technical Conference and Exhibition, Cairo, Egypt, 14–17 February 2010. SPE Paper 126754-MS. [Google Scholar]
- Ozkan, E.; Brown, M.L.; Raghavan, R.S.; Kazemi, H. Comparison of Fractured Horizontal-Well Performance in Conventional and Unconventional Reservoirs. In Proceedings of the SPE Western Regional Meeting, San Jose, CA, USA, 24–26 March 2009. SPE Paper 121290-MS. [Google Scholar]
- Brown, M.; Ozkan, E.; Raghavan, R.; Kazemi, H. Practical Solutions for Pressure-Transient Responses of Fractured Horizontal Wells in Unconventional Shale Reservoirs. SPE Reserv. Eval. Eng. 2011, 14, 663–676. [Google Scholar] [CrossRef]
- Stalgorova, E.; Mattar, L. Practical Analytical Model to Simulate Production of Horizontal Wells with Branch Fractures. In Proceedings of the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012. SPE Paper 162515-MS. [Google Scholar]
- Heidari, S.M.; Clarkson, C.R. An Analytical Model for Analyzing and Forecasting Production from Multi-fractured Horizontal Wells with Complex Branched-Fracture Geometry. SPE Reserv. Eval. Eng. 2015, 18, 356–374. [Google Scholar] [CrossRef]
- Abassi, M.; Sharifi, M.; Kazemi, A. Development of New Analytical Model for Series and Parallel Triple Porosity Models and Providing Transient Shape Factor between Different Regions. J. Hydrol. 2019, 574, 683–698. [Google Scholar] [CrossRef]
- Yao, F. Production Evaluation of Fracturing Horizontal Wells for Solution Gas Drive in Tight Oil Reservoirs; China University of Petroleum (Beijing): Beijing, China, 2018. [Google Scholar]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Shahamat, M.S.; Mattar, L.; Aguilera, R. A Physics-Based Method for Production Data Analysis of Tight and Shale Petroleum Reservoirs Using Succession of Pseudo-Steady States. In Proceedings of the SPE/EAGE European Unconventional Resources Conference and Exhibition, Vienna, Austria, 25–27 February 2014. SPE Paper 167686-MS. [Google Scholar]
- Ogunyomi, B.A. Simple Mechanistic Modeling of Recovery from Unconventional Oil Reservoirs; The University of Texas at Austin: College Station, TX, USA, 2015. [Google Scholar]
- Ogunyomi, B.A.; Patzek, T.W.; Lake, L.W.; Kabir, C.S. History Matching and Rate Forecasting in Unconventional Oil Reservoirs With an Approximate Analytical Solution to the Double-Porosity Model. SPE Reserv. Eval. Eng. 2016, 19, 70–82. [Google Scholar] [CrossRef]
- Qiu, K.X.; Li, H. A New Analytical Solution of the Triple-Porosity Model for History Matching and Performance Forecasting in Unconventional Oil Reservoirs. SPE J. 2018, 23, 2060–2079. [Google Scholar] [CrossRef]
- Qiu, K.X.; Li, H. A New Analytical Model for Production Forecasting in Unconventional Reservior Considering the Simultaneous Matrix-fracture flow. In Proceedings of the Asia Pacific Unconventional Resource Technology Conference, Brisbane, Australia, 18–19 November 2019. SPE Paper URTEC-198266-MS. [Google Scholar]
- Tabatabaie, S.H. Unconventional Reservoirs: Mathematical Modeling of Some Non-linear Problems; University of Calgary: College Station, AB, Canada, 2014. [Google Scholar]
- Behmanesh, H.; Hamdi, H.; Clarkson, C.R.; Thompson, J.M.; Anderson, D.M. Analytical Modeling of Linear Flow in Single-Phase Tight Oil and Tight Gas Reservoirs. J. Pet. Sci. Eng. 2018, 171, 1084–1098. [Google Scholar] [CrossRef]
- Anderson, D.M.; Nobakht, M.; Moghadam, S.; Mattar, L. Analysis of Production Data from Fractured Shale Gas Wells. In Proceedings of the SPE Unconventional Gas Conference, Pittsburgh, PA, USA, 23–25 February 2010. SPE Paper 131787. [Google Scholar]
- Langmuir, I. The Constitution and Fundamental Properties of Solids and Liquids. J. Am. Chem. Soc. 1916, 38, 2221–2295. [Google Scholar] [CrossRef] [Green Version]
- Bumb, A.C.; McKee, C.R. Gas-Well Testing in the Presence of Desorption for Coal bed Methane and Devonian Shale. In Proceedings of the SPE Unconventional Gas Technology Symposium, Louisville, KY, USA, 18–21 May 1986. SPE Paper 15227-MS. [Google Scholar]
- King, G.R. Material Balance Techniques for Coal Seam and Devonian Shale Gas Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, Louisiana, 23–26 September 1990. SPE Paper 20730-MS. [Google Scholar]
- Forchheimer, P. Wasserbewegung Durch Boden. Z. Ver. Deutsch Ing. 1901, 45, 1782–1788. [Google Scholar]
- Wang, J.; Lou, H.S.; Liu, H.Q. An Intergrative Model to Simulate Gas Transport and Production Coupled With Gas Adsorption, Non-Darcy Flow, Surface Diffusion, and Stress Dependence in Organic-Shale Reservoir. SPE J. 2017, 22, 244–264. [Google Scholar] [CrossRef]
- Wang, H.Y.; Porcu, M.M. Impact of Shale-Gas Apparent Permeability on Production: Combined Effects of Non-Darcy Flow/Gas Slippage, Desorption and Geomechanics. SPE Reserv. Eval. Eng. 2015, 18, 495–507. [Google Scholar] [CrossRef]
- Samandarli, O. A New Method for History Matching and Forecasting Shale Gas/Oil Reservoir Production Performance with Dual and Triple Porosity Models; Texas A&M University: College Station, TX, USA, 2011. [Google Scholar]
- Hamdi, H.; Behmanesh, H.; Clarkson, C.R. A Semi-Analytical Approach for Analysis of Wells Exhibiting Multi-Phase Transient Linear Flow: Application to Field Data. In Proceedings of the SPE Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September–2 October 2019. SPE Paper 196164-MS. [Google Scholar]








| Parameter | Value |
|---|---|
| Model dimension (X × Y × Z) (ft) | 80 × 500 × 10 |
| Initial pressure (Psi) | 2500 |
| Bottom-hole pressure (Psi) | 500 |
| Temperature (K) | 318.15 |
| Langmuir volume (Mscf/ton) | 0.096 |
| Langmuir pressure (Psi) | 650 |
| Compressibility (10−6 Psi−1) | 7.5 |
| Matrix porosity | 0.06 |
| Fracture porosity | 0.08 |
| Permeability of hydraulic fracture (mD) | 500 |
| Permeability in region 2 (mD) | 0.0005 |
| Permeability in region 1 (mD) | 0.01 |
| Fracture width (ft) | 0.1 |
| D-factor (Day/Mscf) | 0.0012 |
| Parameter | Value |
|---|---|
| τF (days) | 0.001 |
| τ1 (days) | 22 |
| τ2 (days) | 209 |
| Tr21/Tr1F | 0.09 |
| Tr1F/J | 1.18 |
| qiF (Mscf/D) | 109 |
| Parameter | Given Data | Calculated Value | Relative Error (Vg-Vc)/ Vg × 100% |
|---|---|---|---|
| VpF (ft3) | 40 | 38.37 | 4.1% |
| Vp1 (ft3) | 5970 | 5954 | 0.3% |
| Vp2 (ft3) | 18,000 | 17,455 | 3.0% |
| Case | τF | τ1 | τ2 | Tr21/Tr1F | Tr1F/J | qiF (Mscf/D) | Given Data (ft3) | Calculated Data (ft3) | Relative Error |
|---|---|---|---|---|---|---|---|---|---|
| Case 2 | 0.02 | 9 | 97 | 0.04 | 1.6 | 327 | VpF = 31 | VpF = 32 | 3% |
| Vp1 = 26,258 | Vp1 = 25,137 | 4.3% | |||||||
| Vp2 = 37,512 | Vp2 = 35,343 | 5.8% | |||||||
| Case 3 | 0.01 | 9 | 189 | 0.05 | 1.4 | 252 | VpF = 31 | VpF = 29 | 6.5% |
| Vp1 = 20,084 | Vp1 = 21,123 | 5.2% | |||||||
| Vp2 = 43,686 | Vp2 = 42,387 | 3% | |||||||
| Case 4 | 0.02 | 11 | 106 | 0.05 | 1.3 | 316 | VpF = 31 | VpF = 30 | 3.2% |
| Vp1 = 24,145 | Vp1 = 25,155 | 4.2% | |||||||
| Vp2 = 39,625 | Vp2 = 40,135 | 1.3% |
| Case | τF | τ1 | τ2 | Tr21/Tr1F | Tr1F/J | qiF (Mscf/D) | Given Data (ft3) | Calculated Data (ft3) | Relative Error |
|---|---|---|---|---|---|---|---|---|---|
| Case 5 | 0.02 | 9 | 72 | 0.03 | 1.6 | 990 | VpF = 21 | VpF = 23 | 9.5% |
| Vp1 = 106,022 | Vp1 = 103,820 | 2.1% | |||||||
| Vp2 = 105,281 | Vp2 = 98,054 | 6.7% | |||||||
| Case 6 | 0.03 | 7 | 79 | 0.03 | 2.4 | 937 | VpF = 28 | VpF = 27 | 6.5% |
| Vp1 = 81,062 | Vp1 = 79,302 | 2.2% | |||||||
| Vp2 = 130,234 | Vp2 = 125,139 | 3.8% | |||||||
| Case 7 | 0.02 | 5 | 91 | 0.05 | 1.9 | 911 | VpF = 24 | VpF = 23 | 4.2% |
| Vp1 = 67,264 | Vp1 = 66,097 | 1.7% | |||||||
| Vp2 = 144,036 | Vp2 = 151,950 | 5.5% |
| Parameter | Value |
|---|---|
| Initial pressure (Psi) | 2950 |
| Bottom-hole pressure (Psi) | 480 |
| Temperature (K) | 344.3 |
| Langmuir volume (Scf/ton) | 96 |
| Langmuir pressure (Psi) | 650 |
| Compressibility (Psi−1) | 4 × 10−6 |
| Porosity | 0.06 |
| Parameter | Value |
|---|---|
| τF (days) | 0.01 |
| τ1 (days) | 11 |
| τ2 (days) | 3105 |
| Tr21 / Tr1F | 0.075 |
| Tr1F / J | 0.86 |
| qiF (Mscf/D) | 19,041 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, K.; Li, H. An Analytical Model for Production Analysis of Hydraulically Fractured Shale Gas Reservoirs Considering Irregular Stimulated Regions. Energies 2020, 13, 5899. https://doi.org/10.3390/en13225899
Qiu K, Li H. An Analytical Model for Production Analysis of Hydraulically Fractured Shale Gas Reservoirs Considering Irregular Stimulated Regions. Energies. 2020; 13(22):5899. https://doi.org/10.3390/en13225899
Chicago/Turabian StyleQiu, Kaixuan, and Heng Li. 2020. "An Analytical Model for Production Analysis of Hydraulically Fractured Shale Gas Reservoirs Considering Irregular Stimulated Regions" Energies 13, no. 22: 5899. https://doi.org/10.3390/en13225899
APA StyleQiu, K., & Li, H. (2020). An Analytical Model for Production Analysis of Hydraulically Fractured Shale Gas Reservoirs Considering Irregular Stimulated Regions. Energies, 13(22), 5899. https://doi.org/10.3390/en13225899