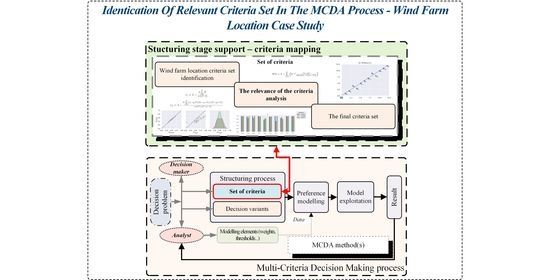
Identification of Relevant Criteria Set in the MCDA Process—Wind Farm Location Case Study
Abstract
:1. Introduction
2. Literature Review
2.1. Renewable Energy Sources
2.2. Application MCDA Methods in RES Domain
- technical aspects of the wind farm operation,
- spatial aspects of wind farm location,
- economic aspects (in particular those related to the planned costs of investment implementation and maintenance),
- a group of social factors resulting from the construction and operation of a wind farm,
- ecological aspects of investment,
- a group of environmental factors surrounding a wind farm,
- legal and political aspects related to the construction of wind farms.
3. Methods
3.1. Conceptual Framework
3.2. The TOPSIS Method
3.3. The VIKOR Method
3.4. The COMET Method
3.5. Similarity Coefficients
4. Results and Discussion
4.1. Rankings Comparison—One Criterion Excluded Case
4.2. Rankings Comparison—Two Criteria Excluded Case
4.3. Rankings Comparison—Three Criteria Excluded Case
4.4. Results Analysis and Discussion
4.5. Results Analysis Based on Utility Values of Decision Variants
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MCDA | Multi-Criteria Decision Analysis |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| VIKOR | VIekriterijumsko KOmpromisno Rangiranje |
| COMET | Characteristic Objects METhod |
| MEJ | Matrix of Expert Judgment |
| SJ | Summed Judgments |
| CO | Characteristic Objects |
| PROMETHEE | Preference Ranking Organization Method for Enrichment Evaluations |
| ELECTRE | ELimination Et Choix Traduisant la REalité |
| ARGUS | Achieving Respect for Grades by Using ordinal Scales only |
| NAIADE | Novel Approach to Imprecise Assessment and Decision Environments |
| ORESTE | Organization, Rangement Et Synthese De Donnes Relationnelles |
| TACTIC | Treatment of the Alternatives aCcording To the Importance of Criteria |
| UTA | UTilités Additives |
| AHP | Analytic Hierarchy Process |
| SMART | Simple Multi-Attribute Rating Technique |
| ANP | Analytic Network Process |
| MACBETH | Measuring Attractiveness by a categorical Based Evaluation Technique |
| MAUT | Multi-Attribute Utility Theory |
| EVAMIX | Evaluation of mixed data |
| PAPRIKA | Potentially All Pairwise RanKings of all possible Alternatives |
| PCCA | Pairwise Criterion Comparison Approach |
| PACMAN | Passive and Active Compensability Multicriteria ANalysis |
| MAPPAC | Multicriterion Analysis of Preferences by means of Pairwise Actions and Criterion comparisons |
| PRAGMA | Preference Ranking Global frequencies in Multicriterion Analysis |
| IDRA | Intercriteria Decision Rule Approach |
| DRSA | Dominance-based Rough Set Approach |
Appendix A
| Excl. | WS | Distance | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| None | 7 | 2 | 8 | 3 | 5 | 7 | 4 | 1 | 12 | 11 | 10 | 9 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 7 | 3 | 9 | 2 | 5 | 6 | 4 | 1 | 12 | 11 | 10 | 8 | 0.9590 | 0.9803 | 0.9842 | 0.1680 | |
| 3 | 2 | 7 | 6 | 4 | 8 | 6 | 1 | 12 | 11 | 9 | 10 | 0.9308 | 0.8585 | 0.9052 | 0.1848 | |
| 3 | 2 | 7 | 6 | 4 | 8 | 5 | 1 | 12 | 11 | 10 | 9 | 0.9389 | 0.8749 | 0.9071 | 0.1358 | |
| 7 | 2 | 9 | 4 | 3 | 6 | 5 | 1 | 12 | 10 | 11 | 8 | 0.9671 | 0.9599 | 0.9632 | 0.2525 | |
| 4 | 2 | 7 | 5 | 6 | 8 | 1 | 3 | 12 | 11 | 10 | 9 | 0.8476 | 0.8598 | 0.9036 | 0.7379 | |
| 7 | 2 | 8 | 5 | 3 | 6 | 4 | 1 | 11 | 12 | 10 | 9 | 0.9619 | 0.9561 | 0.9632 | 0.2323 | |
| 5 | 3 | 8 | 2 | 1 | 4 | 7 | 6 | 12 | 11 | 9 | 10 | 0.6856 | 0.6834 | 0.7810 | 0.7485 | |
| 8 | 3 | 6 | 5 | 4 | 7 | 2 | 1 | 12 | 11 | 10 | 9 | 0.9247 | 0.9330 | 0.9422 | 0.1868 | |
| 7 | 3 | 8 | 2 | 6 | 5 | 4 | 1 | 12 | 10 | 11 | 9 | 0.9538 | 0.9669 | 0.9737 | 0.1851 | |
| 7 | 3 | 9 | 2 | 4 | 6 | 5 | 1 | 12 | 11 | 10 | 9 | 0.9469 | 0.9736 | 0.9824 | 0.1508 |

Appendix B
| Excl. | WS | Distance | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| None | 6 | 3 | 10 | 1 | 5 | 4 | 8 | 2 | 12 | 11 | 9 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 6 | 3 | 11 | 1 | 5 | 4 | 9 | 2 | 12 | 10 | 8 | 7 | 0.9990 | 0.9924 | 0.9860 | 0.0725 | |
| 5 | 3 | 10 | 2 | 6 | 4 | 9 | 1 | 12 | 11 | 7 | 8 | 0.9201 | 0.9634 | 0.9650 | 0.0599 | |
| 6 | 3 | 10 | 1 | 5 | 4 | 9 | 2 | 12 | 11 | 8 | 7 | 0.9991 | 0.9951 | 0.9930 | 0.0149 | |
| 6 | 3 | 11 | 1 | 5 | 4 | 8 | 2 | 12 | 10 | 9 | 7 | 0.9998 | 0.9973 | 0.9930 | 0.0999 | |
| 1 | 4 | 10 | 2 | 9 | 6 | 7 | 3 | 12 | 11 | 8 | 5 | 0.8657 | 0.7660 | 0.8111 | 0.2432 | |
| 6 | 1 | 10 | 2 | 5 | 4 | 9 | 3 | 11 | 12 | 8 | 7 | 0.9008 | 0.9580 | 0.9650 | 0.1080 | |
| 6 | 4 | 10 | 1 | 5 | 3 | 9 | 2 | 12 | 11 | 8 | 7 | 0.9774 | 0.9849 | 0.9860 | 0.0481 | |
| 8 | 5 | 7 | 2 | 4 | 3 | 6 | 1 | 12 | 9 | 10 | 11 | 0.8772 | 0.8682 | 0.8391 | 0.2137 | |
| 6 | 3 | 10 | 1 | 5 | 4 | 8 | 2 | 12 | 11 | 9 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0038 | |
| 6 | 4 | 10 | 1 | 5 | 3 | 9 | 2 | 12 | 11 | 8 | 7 | 0.9774 | 0.9849 | 0.9860 | 0.0944 |

Appendix C
| Excl. | WS | Distance | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| None | 7 | 2 | 8 | 3 | 5 | 7 | 4 | 1 | 12 | 11 | 10 | 9 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 8 | 3 | 9 | 2 | 6 | 4 | 5 | 1 | 12 | 10 | 11 | 7 | 0.9424 | 0.9250 | 0.9317 | 0.3640 | |
| 4 | 2 | 8 | 3 | 7 | 6 | 5 | 1 | 12 | 11 | 10 | 9 | 0.9781 | 0.9406 | 0.9597 | 0.2246 | |
| 5 | 3 | 9 | 2 | 7 | 6 | 4 | 1 | 12 | 10 | 11 | 8 | 0.9473 | 0.9476 | 0.9562 | 0.1715 | |
| 7 | 2 | 10 | 3 | 6 | 4 | 5 | 1 | 11 | 9 | 12 | 8 | 0.9821 | 0.9325 | 0.9212 | 0.2856 | |
| 4 | 5 | 7 | 3 | 8 | 6 | 1 | 2 | 12 | 10 | 11 | 9 | 0.8368 | 0.8201 | 0.8687 | 0.5931 | |
| 7 | 2 | 9 | 3 | 5 | 4 | 6 | 1 | 12 | 11 | 10 | 8 | 0.9797 | 0.9416 | 0.9562 | 0.1956 | |
| 5 | 6 | 8 | 4 | 2 | 1 | 7 | 3 | 12 | 9 | 10 | 11 | 0.7474 | 0.6092 | 0.7215 | 0.7406 | |
| 8 | 5 | 7 | 3 | 6 | 4 | 2 | 1 | 12 | 10 | 11 | 9 | 0.8990 | 0.8835 | 0.9107 | 0.2537 | |
| 7 | 4 | 9 | 2 | 6 | 3 | 5 | 1 | 12 | 11 | 10 | 8 | 0.9178 | 0.8905 | 0.9247 | 0.2262 |

Appendix D
| Excl. | WS | Distance | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| None | 6 | 3 | 10 | 1 | 5 | 4 | 8 | 2 | 12 | 11 | 9 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 6 | 4 | 11 | 1 | 5 | 3 | 9 | 2 | 12 | 10 | 8 | 7 | 0.9773 | 0.9822 | 0.9790 | 0.0763 | |
| 5 | 3 | 10 | 2 | 6 | 4 | 9 | 1 | 12 | 11 | 7 | 8 | 0.9201 | 0.9634 | 0.9650 | 0.0604 | |
| 6 | 3 | 10 | 1 | 5 | 4 | 9 | 2 | 12 | 11 | 8 | 7 | 0.9992 | 0.9952 | 0.9930 | 0.0141 | |
| 6 | 3 | 11 | 1 | 5 | 4 | 8 | 2 | 12 | 10 | 9 | 7 | 0.9998 | 0.9973 | 0.9930 | 0.1021 | |
| 1 | 4 | 10 | 2 | 9 | 5 | 7 | 3 | 12 | 11 | 8 | 6 | 0.8749 | 0.7902 | 0.8322 | 0.2421 | |
| 6 | 1 | 10 | 2 | 5 | 4 | 9 | 3 | 11 | 12 | 8 | 7 | 0.9009 | 0.9580 | 0.9650 | 0.1074 | |
| 6 | 4 | 10 | 1 | 5 | 3 | 9 | 2 | 12 | 11 | 8 | 7 | 0.9775 | 0.9849 | 0.9860 | 0.0496 | |
| 8 | 5 | 7 | 2 | 4 | 3 | 6 | 1 | 12 | 9 | 10 | 11 | 0.8773 | 0.8682 | 0.8392 | 0.2148 | |
| 6 | 4 | 10 | 1 | 5 | 3 | 9 | 2 | 12 | 11 | 8 | 7 | 0.9775 | 0.9849 | 0.9860 | 0.0978 |

Appendix E
| Excl. | WS | Distance | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| None | 7 | 2 | 8 | 3 | 5 | 7 | 4 | 1 | 12 | 11 | 10 | 9 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 9 | 3 | 11 | 2 | 6 | 4 | 5 | 1 | 10 | 8 | 12 | 7 | 0.9398 | 0.8798 | 0.8371 | 0.4478 | |
| 6 | 2 | 8 | 3 | 7 | 4 | 5 | 1 | 11 | 10 | 12 | 9 | 0.9778 | 0.9341 | 0.9387 | 0.2958 | |
| 7 | 2 | 10 | 3 | 6 | 5 | 4 | 1 | 11 | 9 | 12 | 8 | 0.9912 | 0.9583 | 0.9387 | 0.2907 | |
| 6 | 3 | 10 | 4 | 8 | 5 | 1 | 2 | 11 | 9 | 12 | 7 | 0.8730 | 0.8513 | 0.8581 | 0.6261 | |
| 8 | 1 | 9 | 4 | 5 | 3 | 6 | 2 | 11 | 10 | 12 | 7 | 0.8922 | 0.8739 | 0.8862 | 0.6177 | |
| 6 | 5 | 9 | 4 | 2 | 1 | 7 | 3 | 11 | 8 | 12 | 10 | 0.7731 | 0.6388 | 0.7250 | 0.7972 | |
| 8 | 2 | 7 | 5 | 6 | 4 | 3 | 1 | 11 | 9 | 12 | 10 | 0.9536 | 0.9158 | 0.9107 | 0.3371 | |
| 8 | 3 | 10 | 2 | 6 | 4 | 5 | 1 | 12 | 9 | 11 | 7 | 0.9418 | 0.9137 | 0.9107 | 0.3063 |

Appendix F
| Excl. | WS | Distance | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| None | 6 | 3 | 10 | 1 | 5 | 4 | 8 | 2 | 12 | 11 | 9 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 6 | 3 | 12 | 1 | 5 | 4 | 8 | 2 | 11 | 10 | 9 | 7 | 0.9997 | 0.9935 | 0.9790 | 0.1662 | |
| 6 | 2 | 11 | 3 | 5 | 4 | 8 | 1 | 12 | 10 | 9 | 7 | 0.8700 | 0.9618 | 0.9720 | 0.1146 | |
| 6 | 3 | 11 | 1 | 5 | 4 | 8 | 2 | 12 | 10 | 9 | 7 | 0.9998 | 0.9973 | 0.9930 | 0.1020 | |
| 1 | 3 | 11 | 2 | 8 | 6 | 7 | 4 | 12 | 10 | 9 | 5 | 0.8592 | 0.7751 | 0.8252 | 0.2332 | |
| 6 | 1 | 11 | 2 | 5 | 3 | 8 | 4 | 10 | 12 | 9 | 7 | 0.8688 | 0.9371 | 0.9441 | 0.2269 | |
| 6 | 3 | 11 | 1 | 5 | 4 | 8 | 2 | 12 | 10 | 9 | 7 | 0.9998 | 0.9973 | 0.9930 | 0.1154 | |
| 7 | 5 | 9 | 3 | 4 | 2 | 6 | 1 | 11 | 8 | 12 | 10 | 0.8276 | 0.8548 | 0.8322 | 0.2648 | |
| 6 | 3 | 11 | 1 | 5 | 4 | 8 | 2 | 12 | 10 | 9 | 7 | 0.9998 | 0.9973 | 0.9930 | 0.1654 |

References
- Munro, F.R.; Cairney, P. A systematic review of energy systems: The role of policymaking in sustainable transitions. Renew. Sustain. Energy Rev. 2020, 119, 109598. [Google Scholar] [CrossRef]
- Yilan, G.; Kadirgan, M.N.; Çiftçioğlu, G.A. Analysis of electricity generation options for sustainable energy decision making: The case of Turkey. Renew. Energy 2020, 146, 519–529. [Google Scholar] [CrossRef]
- Primc, K.; Slabe-Erker, R. Social policy or energy policy? Time to reconsider energy poverty policies. Energy Sustain. Dev. 2020, 55, 32–36. [Google Scholar] [CrossRef]
- Gupta, J.G.; De, S.; Gautam, A.; Dhar, A.; Pandey, A. Introduction to sustainable energy, transportation technologies, and policy. In Sustainable Energy and Transportation; Springer: Berlin, Germany, 2018; pp. 3–7. [Google Scholar]
- Wang, Q.; Zhan, L. Assessing the sustainability of renewable energy: An empirical analysis of selected 18 European countries. Sci. Total Environ. 2019, 692, 529–545. [Google Scholar] [CrossRef] [PubMed]
- Siksnelyte-Butkiene, I.; Zavadskas, E.K.; Streimikiene, D. Multi-criteria decision-making (MCDM) for the assessment of renewable energy technologies in a household: A review. Energies 2020, 13, 1164. [Google Scholar] [CrossRef] [Green Version]
- Campos-Guzmán, V.; García-Cáscales, M.S.; Espinosa, N.; Urbina, A. Life Cycle Analysis with Multi-Criteria Decision Making: A review of approaches for the sustainability evaluation of renewable energy technologies. Renew. Sustain. Energy Rev. 2019, 104, 343–366. [Google Scholar] [CrossRef]
- Stojčić, M.; Zavadskas, E.K.; Pamučar, D.; Stević, Ž.; Mardani, A. Application of MCDM methods in sustainability engineering: A literature review 2008–2018. Symmetry 2019, 11, 350. [Google Scholar] [CrossRef] [Green Version]
- Shao, M.; Han, Z.; Sun, J.; Xiao, C.; Zhang, S.; Zhao, Y. A review of multi-criteria decision making applications for renewable energy site selection. Renew. Energy 2020, 157, 377–403. [Google Scholar]
- Roy, B. Multicriteria Methodology for Decision Aiding; Springer Science & Business Media: Berlin, Germany, 2013; Volume 12. [Google Scholar]
- Triantaphyllou, E. Multi-criteria decision making methods. In Multi-Criteria Decision Making Methods: A Comparative Study; Springer: Berlin, Germany, 2000; pp. 5–21. [Google Scholar]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Velasquez, M.; Hester, P.T. An analysis of multi-criteria decision making methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Guitouni, A.; Martel, J.M. Tentative guidelines to help choosing an appropriate MCDA method. Eur. J. Oper. Res. 1998, 109, 501–521. [Google Scholar] [CrossRef]
- Roy, B.; Słowiński, R. Questions guiding the choice of a multicriteria decision aiding method. EURO J. Decis. Process. 2013, 1, 69–97. [Google Scholar] [CrossRef] [Green Version]
- Cinelli, M.; Kadziński, M.; Gonzalez, M.; Słowiński, R. How to Support the Application of Multiple Criteria Decision Analysis? Let Us Start with a Comprehensive Taxonomy. Omega 2020, 96, 102261. [Google Scholar] [CrossRef]
- Wątróbski, J.; Jankowski, J.; Ziemba, P.; Karczmarczyk, A.; Zioło, M. Generalised framework for multi-criteria method selection. Omega 2019, 86, 107–124. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Kildienė, S. State of art surveys of overviews on MCDM/MADM methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Xu, L.; Solangi, Y.A. Strategic renewable energy resources selection for Pakistan: Based on SWOT-Fuzzy AHP approach. Sustain. Cities Soc. 2020, 52, 101861. [Google Scholar] [CrossRef]
- Kaya, İ.; Çolak, M.; Terzi, F. A comprehensive review of fuzzy multi criteria decision making methodologies for energy policy making. Energy Strategy Rev. 2019, 24, 207–228. [Google Scholar]
- Pohekar, S.D.; Ramachandran, M. Application of multi-criteria decision making to sustainable energy planning—A review. Renew. Sustain. Energy Rev. 2004, 8, 365–381. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar]
- Moradi, S.; Yousefi, H.; Noorollahi, Y.; Rosso, D. Multi-criteria decision support system for wind farm site selection and sensitivity analysis: Case study of Alborz Province, Iran. Energy Strategy Rev. 2020, 29, 100478. [Google Scholar] [CrossRef]
- Konstantinos, I.; Georgios, T.; Garyfalos, A. A Decision Support System methodology for selecting wind farm installation locations using AHP and TOPSIS: Case study in Eastern Macedonia and Thrace region, Greece. Energy Policy 2019, 132, 232–246. [Google Scholar] [CrossRef]
- Argin, M.; Yerci, V.; Erdogan, N.; Kucuksari, S.; Cali, U. Exploring the offshore wind energy potential of Turkey based on multi-criteria site selection. Energy Strategy Rev. 2019, 23, 33–46. [Google Scholar] [CrossRef]
- Rehman, A.U.; Abidi, M.H.; Umer, U.; Usmani, Y.S. Multi-Criteria Decision-Making Approach for Selecting Wind Energy Power Plant Locations. Sustainability 2019, 11, 6112. [Google Scholar] [CrossRef] [Green Version]
- Deveci, M.; Cali, U.; Kucuksari, S.; Erdogan, N. Interval type-2 fuzzy sets based multi-criteria decision-making model for offshore wind farm development in Ireland. Energy 2020, 198, 117317. [Google Scholar] [CrossRef]
- Gao, J.; Guo, F.; Ma, Z.; Huang, X.; Li, X. Multi-criteria group decision-making framework for offshore wind farm site selection based on the intuitionistic linguistic aggregation operators. Energy 2020, 204, 117899. [Google Scholar] [CrossRef]
- Ziemba, P.; Wątróbski, J.; Zioło, M.; Karczmarczyk, A. Using the PROSA method in offshore wind farm location problems. Energies 2017, 10, 1755. [Google Scholar] [CrossRef] [Green Version]
- Mokarram, M.; Mokarram, M.J.; Gitizadeh, M.; Niknam, T.; Aghaei, J. A novel optimal placing of solar farms utilizing multi-criteria decision-making (MCDA) and feature selection. J. Clean. Prod. 2020, 261, 121098. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, Y.; Wu, C.; He, F.; Zhang, B.; Liu, F. A geographical information system based multi-criteria decision-making approach for location analysis and evaluation of urban photovoltaic charging station: A case study in Beijing. Energy Convers. Manag. 2020, 205, 112340. [Google Scholar] [CrossRef]
- Shorabeh, S.N.; Firozjaei, M.K.; Nematollahi, O.; Firozjaei, H.K.; Jelokhani-Niaraki, M. A risk-based multi-criteria spatial decision analysis for solar power plant site selection in different climates: A case study in Iran. Renew. Energy 2019, 143, 958–973. [Google Scholar] [CrossRef]
- Mokarram, M.; Mokarram, M.J.; Khosravi, M.R.; Saber, A.; Rahideh, A. Determination of the optimal location for constructing solar photovoltaic farms based on multi-criteria decision system and Dempster—Shafer theory. Sci. Rep. 2020, 10, 1–17. [Google Scholar] [CrossRef]
- Mousseau, V.; Figueira, J.; Dias, L.; da Silva, C.G.; Clımaco, J. Resolving inconsistencies among constraints on the parameters of an MCDA model. Eur. J. Oper. Res. 2003, 147, 72–93. [Google Scholar] [CrossRef] [Green Version]
- Dehe, B.; Bamford, D. Development, test and comparison of two Multiple Criteria Decision Analysis (MCDA) models: A case of healthcare infrastructure location. Expert Syst. Appl. 2015, 42, 6717–6727. [Google Scholar] [CrossRef] [Green Version]
- Saaty, T.L. Decision making—The analytic hierarchy and network processes (AHP/ANP). J. Syst. Sci. Syst. Eng. 2004, 13, 1–35. [Google Scholar] [CrossRef]
- Ergu, D.; Kou, G.; Peng, Y.; Shi, Y. A simple method to improve the consistency ratio of the pair-wise comparison matrix in ANP. Eur. J. Oper. Res. 2011, 213, 246–259. [Google Scholar] [CrossRef]
- Wu, Z.; Jin, B.; Fujita, H.; Xu, J. Consensus analysis for AHP multiplicative preference relations based on consistency control: A heuristic approach. Knowl. Based Syst. 2020, 191, 105317. [Google Scholar] [CrossRef]
- Govindan, K.; Jepsen, M.B. ELECTRE: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2016, 250, 1–29. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K. Fuzzy multiple criteria decision-making techniques and applications—Two decades review from 1994 to 2014. Expert Syst. Appl. 2015, 42, 4126–4148. [Google Scholar] [CrossRef]
- Yatsalo, B.; Korobov, A.; Martínez, L. Fuzzy multi-criteria acceptability analysis: A new approach to multi-criteria decision analysis under fuzzy environment. Expert Syst. Appl. 2017, 84, 262–271. [Google Scholar] [CrossRef]
- Piegat, A.; Sałabun, W. Identification of a multicriteria decision-making model using the characteristic objects method. Appl. Comput. Intell. Soft Comput. 2014, 2014, 536492. [Google Scholar] [CrossRef] [Green Version]
- Stanković, M.; Stević, Ž.; Das, D.K.; Subotić, M.; Pamučar, D. A new fuzzy MARCOS method for road traffic risk analysis. Mathematics 2020, 8, 457. [Google Scholar] [CrossRef] [Green Version]
- Panchal, D.; Singh, A.K.; Chatterjee, P.; Zavadskas, E.K.; Keshavarz-Ghorabaee, M. A new fuzzy methodology-based structured framework for RAM and risk analysis. Appl. Soft Comput. 2019, 74, 242–254. [Google Scholar] [CrossRef]
- Amiri, M.; Tabatabaei, M.H.; Ghahremanloo, M.; Keshavarz-Ghorabaee, M.; Zavadskas, E.K.; Antucheviciene, J. A new fuzzy approach based on BWM and fuzzy preference programming for hospital performance evaluation: A case study. Appl. Soft Comput. 2020, 92, 106279. [Google Scholar] [CrossRef]
- Ziemba, P. Towards strong sustainability management—A generalized PROSA method. Sustainability 2019, 11, 1555. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.A.; Shameem, M.; Kumar, R.R.; Hussain, S.; Yan, X. Fuzzy AHP based prioritization and taxonomy of software process improvement success factors in global software development. Appl. Soft Comput. 2019, 83, 105648. [Google Scholar] [CrossRef]
- Gündoğdu, F.K.; Kahraman, C. A novel fuzzy TOPSIS method using emerging interval-valued spherical fuzzy sets. Eng. Appl. Artif. Intell. 2019, 85, 307–323. [Google Scholar] [CrossRef]
- Salih, M.M.; Zaidan, B.; Zaidan, A.; Ahmed, M.A. Survey on fuzzy TOPSIS state-of-the-art between 2007 and 2017. Comput. Oper. Res. 2019, 104, 207–227. [Google Scholar] [CrossRef]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Chen, C.T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Duckstein, L.; Opricovic, S. Multiobjective optimization in river basin development. Water Resour. Res. 1980, 16, 14–20. [Google Scholar] [CrossRef]
- Shekhovtsov, A.; Sałabun, W. A comparative case study of the VIKOR and TOPSIS rankings similarity. Procedia Comput. Sci. 2020, 176, 3730–3740. [Google Scholar] [CrossRef]
- Sałabun, W. The Characteristic Objects Method: A New Distance-based Approach to Multicriteria Decision-making Problems. J. Multi-Criteria Decis. Anal. 2015, 22, 37–50. [Google Scholar] [CrossRef]
- Yu, Q.; Liu, K.; Chang, C.H.; Yang, Z. Realising advanced risk assessment of vessel traffic flows near offshore wind farms. Reliab. Eng. Syst. Saf. 2020, 203, 107086. [Google Scholar] [CrossRef]
- Lee, R.P.; Scheibe, A. The politics of a carbon transition: An analysis of political indicators for a transformation in the German chemical industry. J. Clean. Prod. 2020, 244, 118629. [Google Scholar] [CrossRef]
- Su, C.W.; Umar, M.; Khan, Z. Does fiscal decentralization and eco-innovation promote renewable energy consumption? Analyzing the role of political risk. Sci. Total Environ. 2020, 751, 142220. [Google Scholar] [CrossRef] [PubMed]
- Vo, D.H.; Vo, A.T.; Ho, C.M.; Nguyen, H.M. The role of renewable energy, alternative and nuclear energy in mitigating carbon emissions in the CPTPP countries. Renew. Energy 2020, 161, 278–292. [Google Scholar] [CrossRef]
- Ulucak, R.; Khan, S.U.D. Determinants of the ecological footprint: Role of renewable energy, natural resources, and urbanization. Sustain. Cities Soc. 2020, 54, 101996. [Google Scholar]
- Zhu, D.; Mortazavi, S.M.; Maleki, A.; Aslani, A.; Yousefi, H. Analysis of the robustness of energy supply in Japan: Role of renewable energy. Energy Rep. 2020, 6, 378–391. [Google Scholar] [CrossRef]
- Aydoğan, B.; Vardar, G. Evaluating the role of renewable energy, economic growth and agriculture on CO2 emission in E7 countries. Int. J. Sustain. Energy 2020, 39, 335–348. [Google Scholar] [CrossRef]
- Ghiasi, M.; Esmaeilnamazi, S.; Ghiasi, R.; Fathi, M. Role of Renewable Energy Sources in Evaluating Technical and Economic Efficiency of Power Quality. Technol. Econ. Smart Grids Sustain. Energy 2020, 5, 1. [Google Scholar] [CrossRef] [Green Version]
- Kose, N.; Bekun, F.V.; Alola, A.A. Criticality of sustainable research and development-led growth in EU: The role of renewable and non-renewable energy. Environ. Sci. Pollut. Res. 2020, 27, 12683–12691. [Google Scholar] [CrossRef]
- Lu, Y.; Khan, Z.A.; Alvarez-Alvarado, M.S.; Zhang, Y.; Huang, Z.; Imran, M. A critical review of sustainable energy policies for the promotion of renewable energy sources. Sustainability 2020, 12, 5078. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-turbine and wind-farm flows: A review. Bound. Layer Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maienza, C.; Avossa, A.; Ricciardelli, F.; Coiro, D.; Troise, G.; Georgakis, C.T. A life cycle cost model for floating offshore wind farms. Appl. Energy 2020, 266, 114716. [Google Scholar] [CrossRef]
- Al Irsyad, M.I.; Halog, A.; Nepal, R.; Koesrindartoto, D.P. Economical and environmental impacts of decarbonisation of Indonesian power sector. J. Environ. Manag. 2020, 259, 109669. [Google Scholar] [CrossRef] [PubMed]
- Gnatowska, R.; Moryń-Kucharczyk, E. Current status of wind energy policy in Poland. Renew. Energy 2019, 135, 232–237. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Ma, K. Renewable Energy Systems with Wind Power. In Power Electronics in Renewable Energy Systems and Smart Grid: Technology and Applications; Wiley: New York, NY, USA, 2019; pp. 315–345. [Google Scholar]
- Akbari, N.; Jones, D.; Treloar, R. A cross-European efficiency assessment of offshore wind farms: A DEA approach. Renew. Energy 2020, 151, 1186–1195. [Google Scholar] [CrossRef]
- Pınarbaşı, K.; Galparsoro, I.; Depellegrin, D.; Bald, J.; Pérez-Morán, G.; Borja, Á. A modelling approach for offshore wind farm feasibility with respect to ecosystem-based marine spatial planning. Sci. Total Environ. 2019, 667, 306–317. [Google Scholar] [CrossRef]
- Qazi, A.; Hussain, F.; Rahim, N.A.; Hardaker, G.; Alghazzawi, D.; Shaban, K.; Haruna, K. Towards sustainable energy: A systematic review of renewable energy sources, technologies, and public opinions. IEEE Access 2019, 7, 63837–63851. [Google Scholar] [CrossRef]
- Ilbahar, E.; Cebi, S.; Kahraman, C. A state-of-the-art review on multi-attribute renewable energy decision making. Energy Strategy Rev. 2019, 25, 18–33. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, T.; Xu, C.; Zhang, B.; Li, L.; Ke, Y.; Yan, Y.; Xu, R. Optimal location selection for offshore wind-PV-seawater pumped storage power plant using a hybrid MCDM approach: A two-stage framework. Energy Convers. Manag. 2019, 199, 112066. [Google Scholar] [CrossRef]
- Kheybari, S.; Rezaie, F.M. Selection of biogas, solar, and wind power plants’ locations: An MCDA approach. J. Supply Chain. Manag. Sci. 2020, 1, 45–71. [Google Scholar]
- Abu-Taha, R. Multi-criteria applications in renewable energy analysis: A literature review. In Proceedings of the 2011 Proceedings of PICMET’11: Technology Management in the Energy Smart World (PICMET), Portland, OR, USA, 31 July–4 August 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–8. [Google Scholar]
- Cegan, J.C.; Filion, A.M.; Keisler, J.M.; Linkov, I. Trends and applications of multi-criteria decision analysis in environmental sciences: Literature review. Environ. Syst. Decis. 2017, 37, 123–133. [Google Scholar] [CrossRef]
- Kaya, İ.; Çolak, M.; Terzi, F. Use of MCDM techniques for energy policy and decision-making problems: A review. Int. J. Energy Res. 2018, 42, 2344–2372. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K.; Cavallaro, F.; Khalifah, Z. Sustainable and renewable energy: An overview of the application of multiple criteria decision making techniques and approaches. Sustainability 2015, 7, 13947–13984. [Google Scholar] [CrossRef] [Green Version]
- Wątróbski, J.; Jankowski, J.; Ziemba, P.; Karczmarczyk, A.; Zioło, M. Generalised framework for multi-criteria method selection: Rule set database and exemplary decision support system implementation blueprints. Data Brief 2019, 22, 639. [Google Scholar] [CrossRef]
- Ali, Y.; Butt, M.; Sabir, M.; Mumtaz, U.; Salman, A. Selection of suitable site in Pakistan for wind power plant installation using analytic hierarchy process (AHP). J. Control. Decis. 2018, 5, 117–128. [Google Scholar] [CrossRef]
- Mohsin, M.; Zhang, J.; Saidur, R.; Sun, H.; Sait, S.M. Economic assessment and ranking of wind power potential using fuzzy-TOPSIS approach. Environ. Sci. Pollut. Res. 2019, 26, 22494–22511. [Google Scholar] [CrossRef]
- Solangi, Y.A.; Tan, Q.; Khan, M.W.A.; Mirjat, N.H.; Ahmed, I. The selection of wind power project location in the Southeastern Corridor of Pakistan: A factor analysis, AHP, and fuzzy-TOPSIS application. Energies 2018, 11, 1940. [Google Scholar] [CrossRef] [Green Version]
- Pamučar, D.; Gigović, L.; Bajić, Z.; Janošević, M. Location selection for wind farms using GIS multi-criteria hybrid model: An approach based on fuzzy and rough numbers. Sustainability 2017, 9, 1315. [Google Scholar] [CrossRef] [Green Version]
- Yazdani, M.; Chatterjee, P.; Zavadskas, E.K.; Streimikiene, D. A novel integrated decision-making approach for the evaluation and selection of renewable energy technologies. Clean Technol. Environ. Policy 2018, 20, 403–420. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, J.; Yuan, J.; Geng, S.; Zhang, H. Study of decision framework of offshore wind power station site selection based on ELECTRE-III under intuitionistic fuzzy environment: A case of China. Energy Convers. Manag. 2016, 113, 66–81. [Google Scholar]
- Jun, D.; Tian-tian, F.; Yi-sheng, Y.; Yu, M. Macro-site selection of wind/solar hybrid power station based on ELECTRE-II. Renew. Sustain. Energy Rev. 2014, 35, 194–204. [Google Scholar] [CrossRef]
- Tabaraee, E.; Ebrahimnejad, S.; Bamdad, S. Evaluation of power plants to prioritise the investment projects using fuzzy PROMETHEE method. Int. J. Sustain. Energy 2018, 37, 941–955. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Sałabun, W. A New Approach to Identifying a Multi-Criteria Decision Model Based on Stochastic Optimization Techniques. Symmetry 2020, 12, 1551. [Google Scholar] [CrossRef]
- Sałabun, W.; Wątróbski, J.; Piegat, A. Identification of a multi-criteria model of location assessment for renewable energy sources. In International Conference on Artificial Intelligence and Soft Computing; Springer: Berlin, Germany, 2016; pp. 321–332. [Google Scholar]
- Sánchez-Lozano, J.; García-Cascales, M.; Lamata, M. GIS-based onshore wind farm site selection using Fuzzy Multi-Criteria Decision Making methods. Evaluating the case of Southeastern Spain. Appl. Energy 2016, 171, 86–102. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, C.; Zhang, T. Evaluation of renewable power sources using a fuzzy MCDM based on cumulative prospect theory: A case in China. Energy 2018, 147, 1227–1239. [Google Scholar] [CrossRef]
- Wu, Y.; Geng, S.; Xu, H.; Zhang, H. Study of decision framework of wind farm project plan selection under intuitionistic fuzzy set and fuzzy measure environment. Energy Convers. Manag. 2014, 87, 274–284. [Google Scholar] [CrossRef]
- Marttunen, M.; Lienert, J.; Belton, V. Structuring problems for Multi-Criteria Decision Analysis in practice: A literature review of method combinations. Eur. J. Oper. Res. 2017, 263, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Wątróbski, J.; Ziemba, P.; Jankowski, J.; Zioło, M. Green energy for a green city—A multi-perspective model approach. Sustainability 2016, 8, 702. [Google Scholar] [CrossRef] [Green Version]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Extended VIKOR method in comparison with outranking methods. Eur. J. Oper. Res. 2007, 178, 514–529. [Google Scholar] [CrossRef]
- Chen, S.J.; Hwang, C.L. Fuzzy multiple attribute decision making methods. In Fuzzy Multiple Attribute Decision Making; Springer: Berlin, Germany, 1992; pp. 289–486. [Google Scholar]
- Yoon, K.P.; Hwang, C.L. Multiple Attribute Decision Making: An Introduction; Sage Publications: Thousand Oaks, CA, USA, 1995; Volume 104. [Google Scholar]
- Sałabun, W. Fuzzy Multi-Criteria Decision-Making Method: The Modular Approach in the Characteristic Objects Method. Stud. Proc. Pol. Assoc. Knowl. Manag. 2015, 77, 54–64. [Google Scholar]
- Faizi, S.; Sałabun, W.; Rashid, T.; Wątróbski, J.; Zafar, S. Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry 2017, 9, 136. [Google Scholar] [CrossRef]
- Sałabun, W.; Piegat, A. Comparative analysis of MCDM methods for the assessment of mortality in patients with acute coronary syndrome. Artif. Intell. Rev. 2017, 48, 557–571. [Google Scholar] [CrossRef]
- Hwang, C.L.; Lai, Y.J.; Liu, T.Y. A new approach for multiple objective decision making. Comput. Oper. Res. 1993, 20, 889–899. [Google Scholar] [CrossRef]
- Yoon, K. A reconciliation among discrete compromise solutions. J. Oper. Res. Soc. 1987, 38, 277–286. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple attribute decision making: A state of the art survey. Lect. Notes Econ. Math. Syst. 1981, l186, 58–151. [Google Scholar]
- Shekhovtsov, A.; Kołodziejczyk, J. Do distance-based multi-criteria decision analysis methods create similar rankings? Procedia Comput. Sci. 2020, 176, 3718–3729. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Fan, X.J.; Chen, Y.Z. Site selection in waste management by the VIKOR method using linguistic assessment. Appl. Soft Comput. 2014, 21, 453–461. [Google Scholar] [CrossRef]
- Tong, L.I.; Chen, C.C.; Wang, C.H. Optimization of multi-response processes using the VIKOR method. Int. J. Adv. Manuf. Technol. 2007, 31, 1049–1057. [Google Scholar] [CrossRef]
- Zhang, N.; Wei, G. Extension of VIKOR method for decision making problem based on hesitant fuzzy set. Appl. Math. Model. 2013, 37, 4938–4947. [Google Scholar] [CrossRef]
- Jankowski, J.; Sałabun, W.; Wątróbski, J. Identification of a multi-criteria assessment model of relation between editorial and commercial content in web systems. In Multimedia and Network Information Systems; Springer: Berlin, Germany, 2017; pp. 295–305. [Google Scholar]
- Shekhovtsov, A.; Kołodziejczyk, J.; Sałabun, W. Fuzzy Model Identification Using Monolithic and Structured Approaches in Decision Problems with Partially Incomplete Data. Symmetry 2020, 12, 1541. [Google Scholar] [CrossRef]
- Faizi, S.; Rashid, T.; Sałabun, W.; Zafar, S.; Wątróbski, J. Decision making with uncertainty using hesitant fuzzy sets. Int. J. Fuzzy Syst. 2018, 20, 93–103. [Google Scholar] [CrossRef] [Green Version]
- Sałabun, W.; Palczewski, K.; Wątróbski, J. Multicriteria approach to sustainable transport evaluation under incomplete knowledge: Electric Bikes Case Study. Sustainability 2019, 11, 3314. [Google Scholar] [CrossRef] [Green Version]
- Sałabun, W.; Urbaniak, K. A new coefficient of rankings similarity in decision-making problems. In International Conference on Computational Science; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Pinto da Costa, J.; Soares, C. A weighted rank measure of correlation. Aust. N. Z. J. Stat. 2005, 47, 515–529. [Google Scholar] [CrossRef]
- Sałabun, W.; Wątróbski, J.; Shekhovtsov, A. Are MCDA Methods Benchmarkable? A Comparative Study of TOPSIS, VIKOR, COPRAS, and PROMETHEE II Methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]












| Criterion | Unit | Preference Direction | |
|---|---|---|---|
| yearly amount of energy generated | (MWh) | Max | |
| average wind speed at the height of 100 m | (m/s) | Max | |
| distance from power grid connection | (km) | Min | |
| power grid voltage on the site of connection and its vicinity | (kV) | Max | |
| distance from the road network | (km) | Min | |
| location in Natura 2000 protected area | [0;1] | Min | |
| social acceptance | (%) | Max | |
| investment cost | (PLN) | Min | |
| operational costs per year | (PLN) | Min | |
| profits from generated energy per year | (PLN) | Max |
| 106.78 | 6.75 | 2.00 | 220 | 6.00 | 1 | 52.00 | 455.50 | 8.90 | 36.80 | |
| 86.37 | 7.12 | 3.00 | 400 | 10.00 | 0 | 20.00 | 336.50 | 7.20 | 29.80 | |
| 104.85 | 6.95 | 60.00 | 220 | 7.00 | 1 | 60.00 | 416.00 | 8.70 | 36.20 | |
| 46.60 | 6.04 | 1.00 | 220 | 3.00 | 0 | 50.00 | 277.00 | 3.90 | 16.00 | |
| 69.18 | 7.05 | 33.16 | 220 | 8.00 | 0 | 35.49 | 364.79 | 5.39 | 33.71 | |
| 66.48 | 6.06 | 26.32 | 220 | 6.53 | 0 | 34.82 | 304.02 | 4.67 | 27.07 | |
| 74.48 | 6.61 | 48.25 | 400 | 4.76 | 1 | 44.19 | 349.45 | 4.93 | 28.89 | |
| 73.67 | 6.06 | 19.54 | 400 | 3.19 | 0 | 46.41 | 354.65 | 8.01 | 21.09 | |
| 100.58 | 6.37 | 39.27 | 220 | 8.43 | 1 | 22.07 | 449.42 | 7.89 | 17.62 | |
| 94.81 | 6.13 | 50.58 | 220 | 4.18 | 1 | 21.14 | 450.88 | 5.12 | 17.30 | |
| 48.93 | 7.12 | 21.48 | 220 | 5.47 | 1 | 55.72 | 454.71 | 8.39 | 19.16 | |
| 74.75 | 6.58 | 7.08 | 400 | 9.90 | 1 | 26.01 | 455.17 | 4.78 | 18.44 |
| Excl. | WS | Distance | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| None | 5 | 3 | 10 | 1 | 6 | 4 | 9 | 2 | 12 | 11 | 8 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 5 | 3 | 11 | 1 | 6 | 4 | 9 | 2 | 12 | 10 | 8 | 7 | 0.9998 | 0.9973 | 0.9930 | 0.0771 | |
| 4 | 3 | 10 | 2 | 6 | 5 | 9 | 1 | 12 | 11 | 8 | 7 | 0.9172 | 0.9784 | 0.9860 | 0.0600 | |
| 5 | 3 | 10 | 1 | 6 | 4 | 9 | 2 | 12 | 11 | 8 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0145 | |
| 5 | 2 | 11 | 1 | 6 | 4 | 8 | 3 | 12 | 10 | 9 | 7 | 0.9601 | 0.9811 | 0.9790 | 0.1020 | |
| 1 | 4 | 10 | 2 | 9 | 6 | 8 | 3 | 12 | 11 | 7 | 5 | 0.8709 | 0.8327 | 0.8671 | 0.2042 | |
| 5 | 1 | 10 | 2 | 6 | 4 | 9 | 3 | 11 | 12 | 8 | 7 | 0.9016 | 0.9628 | 0.9720 | 0.1180 | |
| 5 | 4 | 10 | 1 | 6 | 3 | 9 | 2 | 12 | 11 | 8 | 7 | 0.9782 | 0.9897 | 0.9930 | 0.0559 | |
| 8 | 5 | 7 | 2 | 4 | 3 | 6 | 1 | 12 | 9 | 10 | 11 | 0.8678 | 0.8165 | 0.7832 | 0.2738 | |
| 5 | 3 | 10 | 1 | 6 | 4 | 9 | 2 | 12 | 11 | 8 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0037 | |
| 5 | 3 | 10 | 1 | 6 | 4 | 9 | 2 | 12 | 11 | 8 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0890 |
| Excl. | WS | Distance | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| None | 5 | 3 | 10 | 1 | 6 | 4 | 9 | 2 | 12 | 11 | 8 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 5 | 3 | 11 | 1 | 6 | 4 | 9 | 2 | 12 | 10 | 8 | 7 | 0.9998 | 0.9973 | 0.9930 | 0.0808 | |
| 4 | 3 | 10 | 2 | 6 | 5 | 9 | 1 | 12 | 11 | 8 | 7 | 0.9173 | 0.9785 | 0.9860 | 0.0606 | |
| 5 | 3 | 10 | 1 | 6 | 4 | 9 | 2 | 12 | 11 | 8 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0138 | |
| 5 | 2 | 11 | 1 | 6 | 4 | 8 | 3 | 12 | 10 | 9 | 7 | 0.9602 | 0.9812 | 0.9790 | 0.1037 | |
| 1 | 4 | 10 | 2 | 9 | 6 | 8 | 3 | 12 | 11 | 7 | 5 | 0.8710 | 0.8327 | 0.8671 | 0.2033 | |
| 5 | 1 | 10 | 2 | 6 | 4 | 9 | 3 | 11 | 12 | 8 | 7 | 0.9017 | 0.9629 | 0.9720 | 0.1173 | |
| 5 | 4 | 10 | 1 | 6 | 3 | 9 | 2 | 12 | 11 | 8 | 7 | 0.9783 | 0.9898 | 0.9930 | 0.0573 | |
| 8 | 5 | 7 | 2 | 4 | 3 | 6 | 1 | 12 | 9 | 10 | 11 | 0.8679 | 0.8166 | 0.7832 | 0.2747 | |
| 5 | 3 | 10 | 1 | 6 | 4 | 9 | 2 | 12 | 11 | 8 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0912 |
| Excl. | WS | Distance | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| None | 5 | 3 | 10 | 1 | 6 | 4 | 9 | 2 | 12 | 11 | 8 | 7 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 5 | 3 | 12 | 1 | 6 | 4 | 9 | 2 | 11 | 10 | 8 | 7 | 0.9997 | 0.9935 | 0.9790 | 0.1693 | |
| 5 | 2 | 11 | 3 | 6 | 4 | 9 | 1 | 12 | 10 | 8 | 7 | 0.8700 | 0.9618 | 0.9720 | 0.1151 | |
| 5 | 2 | 11 | 1 | 6 | 4 | 9 | 3 | 12 | 10 | 8 | 7 | 0.9610 | 0.9860 | 0.9860 | 0.1032 | |
| 1 | 3 | 11 | 2 | 9 | 6 | 7 | 4 | 12 | 10 | 8 | 5 | 0.8600 | 0.8139 | 0.8462 | 0.2011 | |
| 6 | 1 | 11 | 2 | 5 | 4 | 9 | 3 | 10 | 12 | 8 | 7 | 0.8945 | 0.9500 | 0.9510 | 0.2428 | |
| 6 | 2 | 11 | 1 | 5 | 4 | 9 | 3 | 12 | 10 | 8 | 7 | 0.9539 | 0.9779 | 0.9790 | 0.1193 | |
| 7 | 5 | 9 | 3 | 4 | 2 | 6 | 1 | 11 | 8 | 12 | 10 | 0.8194 | 0.8031 | 0.7692 | 0.3153 | |
| 6 | 3 | 11 | 1 | 5 | 4 | 9 | 2 | 12 | 10 | 8 | 7 | 0.9928 | 0.9892 | 0.9860 | 0.1571 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kizielewicz, B.; Wątróbski, J.; Sałabun, W. Identification of Relevant Criteria Set in the MCDA Process—Wind Farm Location Case Study. Energies 2020, 13, 6548. https://doi.org/10.3390/en13246548
Kizielewicz B, Wątróbski J, Sałabun W. Identification of Relevant Criteria Set in the MCDA Process—Wind Farm Location Case Study. Energies. 2020; 13(24):6548. https://doi.org/10.3390/en13246548
Chicago/Turabian StyleKizielewicz, Bartłomiej, Jarosław Wątróbski, and Wojciech Sałabun. 2020. "Identification of Relevant Criteria Set in the MCDA Process—Wind Farm Location Case Study" Energies 13, no. 24: 6548. https://doi.org/10.3390/en13246548
APA StyleKizielewicz, B., Wątróbski, J., & Sałabun, W. (2020). Identification of Relevant Criteria Set in the MCDA Process—Wind Farm Location Case Study. Energies, 13(24), 6548. https://doi.org/10.3390/en13246548