Wind Farm Fault Detection by Monitoring Wind Speed in the Wake Region
Abstract
:1. Introduction
2. Fluid Field Simulation in Wind Farm
2.1. Governing Equations and Numerical Method
2.2. Computational Domain and Simulation Conditions
2.3. Validation of Source Term
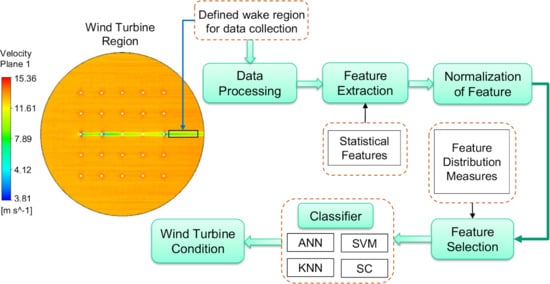
3. Wind Farm Fault Detection Methodology
3.1. Overview
3.2. Feature Extraction
3.3. Feature Selection
- (1)
- From the normal distribution of feature into each class , calculate the mean values and STDs for each group.
- (2)
- Calculate the distance between every two groups for each feature based on the mean values:
- (3)
- Check probability overlapping in the significant range using the ratio of
- (4)
- Rank the features following the condition:
- (5)
- Remove irrelevant features that have a small value of
3.4. Artificial Machine Learning Classifiers
4. Results and Discussions
5. Conclusions
- A wind farm model was presented by adding the flow kinetic energy loss model in the turbine region. This model was able to simulate the nonlinear wind field without the information of thrust force. The simulation result was qualitatively consistent with the actual characteristics of the wind measured at the turbine wake side.
- A new feature selection algorithm specifically designed for the wind speed monitoring was proposed. Due to the volatile characteristic of wind flow, this algorithm took the distribution of the features into account and ranked them in terms of their relevance to the classification. The proposed algorithm proved to have a better performance than the FEM and RFE under a limited feature number.
- The faults in a wind turbine array were detected by measuring the wind velocity difference in the wake region. The performance of several machine learning methods, such as SC, KNN, SVM, and ANN, were presented and compared. It was confirmed that 96% accuracy could be achieved for single fault detection with 10 selected features, and 94.44% accuracy could be achieved for two-fault detection with 9 selected features.
- The success of the novel fault detection scheme presented in this study provides significant potential for remote monitoring and diagnosis of offshore wind farms. Not only single fault but also multi-faults in wind turbines can be well detected by measuring the wind speed.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ANN | Artificial neural network |
| CFD | Computational fluid dynamics |
| FEM | Fuzzy entropy measures |
| KNN | k-nearest neighbors |
| Kur | Kurtosis value of wind speed |
| RFE | Recursive feature elimination methods |
| RMS | Root mean square value of wind speed |
| SC | Similarity classifier |
| SVM | Support vector machine |
| STD | Standard deviation value of wind speed |
| Var | Variance value of wind speed |
| C | Class set |
| D | Diameter of wind turbine, m |
| di,j | Distance between every two groups |
| Distance between an unseen observation and each training observation | |
| f(x) | Activate function |
| Ii | Ideal vector |
| k | Turbulence kinetic energy |
| k-ɛ | Standard turbulence model |
| P | Conditional probability |
| Pl | Feature raking measure |
| Pressure, N/m2 | |
| S | Source term |
| S(x, I) | Similarities |
| V | Velocity, m/s |
| Vx | Wind speed in the x-direction, m/s |
| Vy | Wind speed in the y-direction, m/s |
| Vz | Wind speed in the z-direction, m/s |
| u0 | Velocity at the reference height zr, m/s |
| u(z) | Vertical velocity profile, m/s |
| x | Horizontal-axis, m |
| Set of inputs | |
| x/D | Distance behind the wind turbine along the horizontal-axis |
| Outputs | |
| wi | Weight between neurons |
| wr | Weight of each dimension |
| α | Specific exponent |
| ɛ | Dissipation rate of turbulence energy |
| μ | Mean value of each group |
| σ | Standard deviation of each group |
| θ | Threshold |
| ∇ | Divergence |
| ρ | Density, kg/m3 |
References
- Ladenburg, J. Attitudes towards on-land and offshore wind power development in Denmark; choice of development strategy. Renew. Energy 2008, 33, 111–118. [Google Scholar]
- Christensen, J.J.; Andersson, C.; Gutt, S. Remote condition monitoring of Vestas turbines. In Proceedings of the European Wind Energy Conference, Marseille, France, 16–19 March 2009; pp. 1–10. [Google Scholar]
- Yang, S.; Li, W.; Wang, C. The intelligent fault diagnosis of wind turbine gearbox based on artificial neural network. In Proceedings of the International Conference on Condition Monitoring and Diagnosis, Beijing, China, 21–24 April 2008; pp. 1327–1330. [Google Scholar]
- Bennouna, O.; Héraud, N.; Camblong, H.; Rodriguez, M. Diagnosis of the Doubly-Fed Induction Generator of a Wind Turbine. Wind. Eng. 2005, 29, 431–447. [Google Scholar]
- Widodo, A.; Kim, E.Y.; Son, J.-D.; Yang, B.-S.; Tan, A.C.; Gu, D.-S.; Choi, B.-K.; Mathew, J. Fault diagnosis of low speed bearing based on relevance vector machine and support vector machine. Expert Syst. Appl. 2009, 36, 7252–7261. [Google Scholar]
- Caselitz, P.; Giebhardt, J.; Krüger, T.; Mevenkamp, M. Development of a fault detection system for wind energy converters. In Proceedings of the European Union Wind Energy Conference, Göteborg, Sweden, 20–24 May 1996; pp. 1004–1007. [Google Scholar]
- Guo, P.; Infield, D.; Yang, X. Wind Turbine Generator Condition-Monitoring Using Temperature Trend Analysis. IEEE Trans. Sustain. Energy 2011, 3, 124–133. [Google Scholar]
- Qiao, W.; Lu, D. A Survey on Wind Turbine Condition Monitoring and Fault Diagnosis—Part II: Signals and Signal Processing Methods. IEEE Trans. Ind. Electron. 2015, 62, 6546–6557. [Google Scholar]
- Hameed, Z.; Hong, Y.; Cho, Y.; Ahn, S.-H.; Song, C. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew. Sustain. Energy Rev. 2009, 13, 1–39. [Google Scholar]
- Nie, M.; Wang, L. Review of Condition Monitoring and Fault Diagnosis Technologies for Wind Turbine Gearbox. Procedia CIRP 2013, 11, 287–290. [Google Scholar]
- Koulocheris, D.; Gyparakis, G.; Stathis, A.; Costopoulos, T. Vibration Signals and Condition Monitoring for Wind Turbines. Engineering 2013, 5, 948–955. [Google Scholar] [CrossRef] [Green Version]
- Igba, J.; Alemzadeh, K.; Durugbo, C.; Eiriksson, E.T. Analysing RMS and peak values of vibration signals for condition monitoring of wind turbine gearboxes. Renew. Energy 2016, 91, 90–106. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Qiao, W.; Peng, Y.; Cheng, F.; Qu, L. Quantitative Evaluation of Wind Turbine Faults Under Variable Operational Conditions. IEEE Trans. Ind. Appl. 2016, 52, 2061–2069. [Google Scholar] [CrossRef]
- Cheng, F.; Peng, Y.; Qu, L.; Qiao, W. Current-based Fault Detection and Identification for Wind Turbine Drivetrain Gearboxes. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Portland, OR, USA, 2–6 October 2016. [Google Scholar]
- Salameh, J.P.; Cauet, S.; Etien, E.; Sakout, A.; Rambault, L. Gearbox condition monitoring in wind turbines: A review. Mech. Syst. Signal Process. 2018, 111, 251–264. [Google Scholar] [CrossRef]
- Lu, B.; Li, Y.; Wu, X.; Yang, Z. A review of recent advances in wind turbine condition monitoring and fault diagnosis. In Proceedings of the 2009 IEEE Power Electronics and Machines in Wind Applications, Lincoln, NE, USA, 24–26 June 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Kabir, M.J.; Oo, A.M.T.; Rabbani, M. A Brief Review on Offshore Wind Turbine Fault Detection and Recent Development in Condition Monitoring Based Maintenance System; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2015; pp. 1–7. [Google Scholar]
- Lu, W.; Chu, F. Condition monitoring and fault diagnostics of wind turbines. In Proceedings of the 2010 Prognostics and System Health Management Conference, Macau, China, 12–14 January 2010; pp. 1–11. [Google Scholar]
- Menke, R.; Vasiljević, N.; Hansen, K.S.; Hahmann, A.N.; Mann, J. Does the wind turbine wake follow the topography? A multi-lidar study in complex terrain. Wind Energy Sci. 2018, 3, 681–691. [Google Scholar] [CrossRef] [Green Version]
- Kermani, A.; Andersen, S.; Sørensen, N.; Shen, W. Analysis of turbulent wake behind a wind turbine. In Proceedings of the International Conference on Aerodynamics of Offshore Wind Energy Systems and Wakes, Copenhagen, Denmark, 17–19 June 2013. [Google Scholar]
- Schümann, H.; Pierella, F.; Saetran, L. Experimental Investigation of Wind Turbine Wakes in the Wind Tunnel. Energy Procedia 2013, 35, 285–296. [Google Scholar]
- Ainslie, J. Calculating the flowfield in the wake of wind turbines. J. Wind. Eng. Ind. Aerodyn. 1988, 27, 213–224. [Google Scholar]
- Talmon, A.M. The Wake of a Horizontal-axis Wind Turbine Model. Measurements in Uniform Approach Flow and in a Simulated Atmospheric Boundary Layer; Report 85-010121, TNO Apeldoorn; TNO Division of Technology for Society Technology: The Hague, The Netherlands, 1985. [Google Scholar]
- Göçmen, T.; Van der Laan, P.; Réthoré, P.E.; Diaz, A.P.; Larsen, G.C.; Ott, S. Wind turbine wake models developed at the technical university of Denmark: A review. Renew. Sustain. Energy Rev. 2016, 60, 752–769. [Google Scholar]
- Sedaghatizadeh, N.; Arjomandi, M.; Kelso, R.; Cazzolato, B.S.; Ghayesh, M.H. Modelling of wind turbine wake using large eddy simulation. Renew. Energy 2018, 115, 1166–1176. [Google Scholar]
- Hansen, M.O.L. Aerodynamics of Wind Turbine, 2nd ed.; Earthscan Publication Ltd.: London, UK, 2008. [Google Scholar]
- Fuertes, F.C.; Porté-Agel, F. Using a Virtual Lidar Approach to Assess the Accuracy of the Volumetric Reconstruction of a Wind Turbine Wake. Remote Sens. 2018, 10, 721. [Google Scholar]
- Beck, H.; Kühn, M. Reconstruction of Three-Dimensional Dynamic Wind-Turbine Wake Wind Fields with Volumetric Long-Range Wind Doppler LiDAR Measurements. Remote Sens. 2019, 11, 2665. [Google Scholar]
- Bromm, M.; Rott, A.; Beck, H.; Vollmer, L.; Steinfeld, G.; Kühn, M. Field investigation on the influence of yaw misalignment on the propagation of wind turbine wakes. Wind Energy 2018, 21, 1011–1028. [Google Scholar]
- Newman, J.F.; Bonin, T.; Kastner-Klein, P.; Wharton, S.; Newsom, R.K. Testing and validation of multi-lidar scanning strategies for wind energy applications. Wind Energy 2016, 19, 2239–2254. [Google Scholar]
- Van Dooren, M.F.; Trabucchi, D.; Kühn, M. A Methodology for the Reconstruction of 2D Horizontal Wind Fields of Wind Turbine Wakes Based on Dual-Doppler Lidar Measurements. Remote Sens. 2016, 8, 809. [Google Scholar]
- Wildmann, N.; Päschke, E.; Roiger, A.; Mallaun, C. Towards improved turbulence estimation with Doppler wind lidar velocity-azimuth display (VAD) scans. Atmos. Meas. Tech. 2020, 13, 4141–4158. [Google Scholar]
- ANSYS. ANSYS FLUENT 14.0 Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- ANSYS. ANSYS FLUENT 14.0 User’s Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- IEC. Wind Turbines—Part 12-1: Power Performance Measurements of Electricity Producing Wind Turbines; IEC 61400-12-1; IEC: Geneva, Switzerland, 2017. [Google Scholar]
- Betz, A. Introduction to the Theory of Flow Machines; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Launder, B.; Spalding, D. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar]
- ANSYS. ANSYS FLUENT UDF Manual; ANSYS, Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Hsu, S.A.; Meindl, E.A.; Gilhousen, D.B. Determining the power-law wind-profile exponent under near-neutral stability conditions at sea. J. Appl. Meteorol. 1994, 33, 757–765. [Google Scholar]
- Lee, S.; Kwon, S.-D. Improvement of Aerodynamic Performance and Energy Supply of Bridges Using Small Wind Turbines. J. Bridge Eng. 2015, 20, 04014116. [Google Scholar]
- Kupinski, M.A.; Giger, M.L. Feature selection and classifiers for the computerized detection of mass lesions in digital mammography. In Proceedings of the International Conference on Neural Networks, Houston, TX, USA, 9–12 June 1997; pp. 2460–2463. [Google Scholar]
- Janecek, A.; Demel, M.; Gansterer, W.; Ecker, G.F. On the Relationship between Feature Selection and Classification Accuracy. J. Mach. Learn. Res. 2008, 4, 90–105. [Google Scholar]
- Luukka, P.; Saastamoinen, K.; Könönen, V. A Classifier Based on Maximal Fuzzy Similarity in Generalized Lukasiewicz Structure. In Proceedings of the FUZZ-IEEE 2001 Conference, Melbourne, Australia, 2–5 December 2001. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar]
- Avossa, A.; DeMartino, C.; Contestabile, P.; Ricciardelli, F.; Vicinanza, D. Some Results on the Vulnerability Assessment of HAWTs Subjected to Wind and Seismic Actions. Sustainability 2017, 9, 1525. [Google Scholar]










| Selected Feature | SC (%) | KNN (%) | SVM (%) | ANN (%) |
|---|---|---|---|---|
| 4 | 76 | 72 | 57.14 | 73.33 |
| all | 96 | 96 | 95.23 | 96.67 |
| 10 | 96 | 96 | 95.23 | 96.67 |
| Selected Feature | SC (%) | KNN (%) | SVM (%) | ANN (%) |
|---|---|---|---|---|
| 3 | 75 | 76.19 | 62.62 | 61.11 |
| all | 88.09 | 90.47 | 88.09 | 90.47 |
| 9 | 94.44 | 92.86 | 92.42 | 94.44 |
| Rank | FEM | RFE | New Method |
|---|---|---|---|
| 1 | STD_y | Kur_z | Kur_x |
| 2 | Kur_y | STD_y | Kur_y |
| 3 | Var_x | STD_x | Kur_z |
| 4 | RMS_x | Var_y | STD_y |
| 5 | STD_z | Var_x | STD_z |
| 6 | STD_x | STD_z | Var_x |
| 7 | Kur_z | Kur_y | RMS_x |
| 8 | RMS_y | RMS_x | STD_x |
| 9 | Kur_x | Kur_x | Var_y |
| 10 | RMS_z | Var_z | RMS_y |
| 11 | Var_y | RMS_y | RMS_z |
| 12 | Var_z | RMS_z | Var_z |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, M.-Q.; Li, Y.-C.; Lan, C.-Y.; Liu, M.-K. Wind Farm Fault Detection by Monitoring Wind Speed in the Wake Region. Energies 2020, 13, 6559. https://doi.org/10.3390/en13246559
Tran M-Q, Li Y-C, Lan C-Y, Liu M-K. Wind Farm Fault Detection by Monitoring Wind Speed in the Wake Region. Energies. 2020; 13(24):6559. https://doi.org/10.3390/en13246559
Chicago/Turabian StyleTran, Minh-Quang, Yi-Chen Li, Chen-Yang Lan, and Meng-Kun Liu. 2020. "Wind Farm Fault Detection by Monitoring Wind Speed in the Wake Region" Energies 13, no. 24: 6559. https://doi.org/10.3390/en13246559
APA StyleTran, M. -Q., Li, Y. -C., Lan, C. -Y., & Liu, M. -K. (2020). Wind Farm Fault Detection by Monitoring Wind Speed in the Wake Region. Energies, 13(24), 6559. https://doi.org/10.3390/en13246559