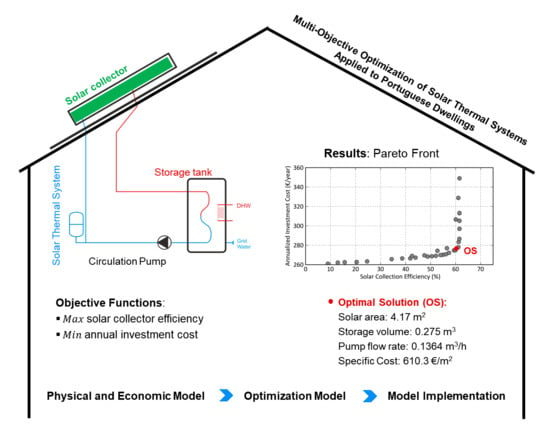
Multi-Objective Optimization of Solar Thermal Systems Applied to Portuguese Dwellings

Abstract

Solar thermal systems have been widely used to increase energy efficiency in the building sector, since the use of renewable energy sources became one of the top priorities to meet environmental targets. The main objective of this study is the thermo-economic optimization of solar thermal systems for residential building applications, considering a multi-objective approach. The simulations were performed through a MatLab code by implementing an elitist variant of Non-dominated Sorting Genetic Algorithm-II (NASGA-II). The solar collection area and the linear loss coefficient as well as the tank storage volume were defined as decision variables. A two-dimensional Pareto front was obtained, considering as objective functions the minimization of the annualized investment cost and the maximization of the solar collection efficiency. Based on the best trade-off between both objectives and considering that the solar thermal systems can operate for a period of at least 15 years, the Pareto analysis led to the conclusion that a system with an annualized investment cost between 270 and 280 €/year allows reaching a collection efficiency of 60%. After the analysis of the optimal solution points, a configuration was selected to estimate the system total purchasing cost: a panel with a solar area of 4.17 m² and with a linear coefficient loss of 3.684 W/m².K; a storage volume of 0.275 m³; and a pump flow rate of 0.1364 m³/h. For this configuration, we estimated a total purchasing cost of 2545.0 €, whereas the solar collector and the storage tank are the most expensive components, representing a share of 42% and 43%, respectively. These results represent a specific cost of 610.3 €/m² per solar collection area.

1. Introduction

Solar energy is the most abundant and cleaner renewable energy resource and it can be supplied with minimal environmental impact. Sun uniformly sends solar radiation through space, but only about 1367 W/m² reaches the Earth atmosphere [1]. The amount of solar energy received on a 1 m² surface during a time interval can be calculated by integrating the irradiance over that time interval. This energy, also called solar irradiation or insolation, has two main components: the direct and the diffuse solar radiation [1,2,3]. The geographical coordinates, the topography, and the climate conditions of a certain location are the three main parameters that affect the effectiveness of solar thermal systems in converting direct and diffuse radiation into useful energy [4].

The demand of solar thermal systems is estimated to grow by 20% per year, depending on the collector working area, availability of the solar radiation throughout the year, and the type of solar thermal systems [5].

1.1. Technology Background

A solar thermal system converts the solar energy into thermal energy, which can be used for domestic hot water (DHW) production, space heating and cooling, or to heat swimming pools’ water. These systems can be classified according to the type of thermal fluid used to transport the heat from the collector (air, pure water, refrigerants, and water–glycol mixtures). Usually, a mixture of water and glycol is mainly used for DHW and to partly cover the heating energy demand of a building. Systems should be able to provide the required heat demand at low and medium- temperature ranges, from 40 to 80 °C, which corresponds to the largest share of heat consumption in DHW and space heating [6,7]. Therefore, the solar collectors are the key elements of the solar thermal systems because the collector technology should be able to meet the application needs at the lowest cost [6]. The thermal collector converts the solar radiation in thermal energy, which is further transferred to a thermal fluid circulating through the panel. They are categorized into two categories, the non-concentrating (flat plate or evacuated tubes) and concentrating collectors, in the solar radiation concentration devices. Concerning the non-concentrating thermal collector, the flat ones (pipes are required to connect the two components) include several components: a transparent glazed cover, pipes, absorber, and a thermal insulation layer. In turn, the evacuated tubes’ solar thermal collector consists of absorbers, glazed tubes, heat pipes, and insulated casing [1,2,8]. For both systems, the absorber plays an important role in heat transfer process, requiring a good thermal conductivity. In addition, the insulation between the absorber and the collector casing requires optimization to reduce the thermal losses. Such aspects require the use of more expensive materials, increasing the investment costs of solar thermal collectors [9,10].

In regions where the outdoor ambient temperature decreases below the water freezing point, a mixture of water and ethylene or propylene glycol (antifreeze) has to be used [1]. However, due to the organic component in the antifreeze mixture, these thermal fluids need to be replaced within 3 to 5 years, as a result of its degradation because of the higher temperatures in stagnation periods [11]. Air can also be used as a thermal fluid in solar thermal systems, but its use demands systems with large ducts to guarantee the higher the heat transfer efficiency. For systems operating with air, issues such as leakages, system location, or refilling are not a problem [12]. Some refrigerants, molten salts, and oil-based fluids are used by hybrid or concentrated solar thermal systems, which operate at high temperatures (varying between 350 and 900 °C) [13].

Solar thermal systems can be classified into natural and forced circulation systems. Natural circulation systems consist of a storage tank and a solar thermal collector, where the thermal fluid circulates by density gradients. The solar thermal collector can be either a flat plate or a different configuration having evacuated tubes that are directly inserted in the storage tank [9]. Forced circulation systems include the solar thermal collector, the storage tank, and a hydraulic pump used to force the thermal fluid circulation between these components (Figure 1). Usually, the pump is switched on/off by a solar controller that compares the measured water temperature in the collector with the temperature measured in the storage tank [14]. For mild climate locations, these systems can operate with a closed-loop, but for locations where the outdoor temperature can reach temperatures below 0 °C, the solar thermal systems operates as an open-loop circuit. In those circumstances, a solution is added to the thermal fluid to avoid water freezing while flowing in the external components. The flow is controlled by a set of valves that depend on the temperature measured at the collector. In practical terms, when the temperature reaches 0 °C, the water from the storage tank is prevented from passing to the solar collector by the valves, and the water from the solar collector is drained (Figure 1a). When the solar collector temperature increases and becomes higher than the storage tank temperature, the solar controller switches back, and the solar collector is filled up with water from the mains [2,14,15]. Severe outdoor conditions (i.e., the outside temperature is frequently below 0 °C) require the use of an antifreeze solution as thermal fluid (mostly to flow in exterior pipes of solar collector) and the installation of a heat exchanger to separate the domestic hot water circuit from the solar circuit. For these types of applications (Figure 1b), it is required to add an expansion vessel to manage the thermal fluid volume variations with the temperature and an internal heat exchanger is installed in the storage tank [9,15,16].

1.2. Brief Literature Review

Most of the literature concerning the analysis of solar thermal systems investigates a specific technology aiming to assess the thermal system efficiency, the system’s operational conditions, or the best technological solution and appropriate size for a specific application [8,17,18,19,20]. Kalogirou [15] reviewed several types of solar thermal collectors, such as flat-plate, parabolic trough, evacuated tube, Fresnel lens, or parabolic dish, for different applications, e.g., solar water heating, integrated collector storage, space heating and cooling, air and water systems, heat pumps, and refrigeration appliances. Ong and Tong [20] studied a solar water heater with a specific design of a solar collector and storage tank. The system was sized considering distinct weather conditions (ambient temperature and solar radiation intensity). Marion et al. [21] developed a theoretical model in which a heat transfer equation was defined to predict the thermal equilibrium state of a glazed flat plate collector, considering different operational conditions. They have concluded that the optimal condition linearly depends on solar radiation. In addition, the net mechanical power is mostly affected by the fluid mass flow rate. Yongga et al. [22] studied a novel facade solar thermal system performance in summer and winter conditions. The research aimed to evaluate the efficiency of a new flat-plate collector and indoor radiation plate design, in avoiding extreme variations of the indoor thermal environment. The latest technological innovation such as the direct integration of collectors within the roofs or façades structure has shown the potentiality of being capable of regulating and optimizing the energy flows between the indoor and outdoor environments [23,24]. Islam and Morimoto [5] presented a state-of-the-art review of non-concentrating solar thermal systems, describing the design of current technology as well as the material selection criteria and engineering limitations.

The implementation of solar thermal systems has been studied in different regions, with different climatic conditions and in countries whose economic considerations for their application are very different. Artur et al. [25] applied a survey to understand the transition of current domestic hot water technology to solar thermal systems in urban areas (Maputo, Mozambique). The study demonstrated a positive outcome regarding the reduction of electricity demand and the consequent economic savings. The transition depends on the household income, governmental policies, and incentives to subsidize the technology adaptation. Košičan et al. [26] studied a solar thermal panel for space heating by determining the best design scheme for industrial and office buildings. The study was focused on the thermal energy performance of ventilated double skin façades in order to improve the thermal comfort in buildings. The authors compared different solar thermal systems considering energy, technical, economical, and commercial availability as criteria for four applications in Spain. It was concluded that there is no universal best solar thermal scheme. The choice for a particular solar thermal system is influenced by the energy consumption, technical conditions, location, and economic criteria. Sami et al. [27] published an interesting study regarding the integration of solar thermal systems (water heating) into high-energy performance housing in various regions with distinct climatic conditions in Algeria. The study considered both economic and energy criteria and allowed determining the optimal collector area that minimized the purchase and installation costs. Louvet et al. [28] used the levelized cost of energy to determine the heat cost per kWh of final energy produced by solar thermal systems in five European countries, considering different residential systems. It was concluded that it is of utmost importance to focus the research on solar assisted systems in order to reduce prices and increase the system’s lifetime to cut off the economic gap when compared with the conventional heating systems. In most of the countries in study (Austria, Denmark, France, Germany, and Switzerland), the heat cost per kWh of final energy is higher for the solar-assisted heating systems, which are not subsidized. A similar study was also presented by Gautam et al. [29], who have also concluded that the high initial costs of solar thermal plants are not cost-effective when compared to the conventional technologies. Tschopp et al. [30] compared the market growth of solar thermal systems in Denmark, Germany, China, and Austria. The authors concluded that the stability of the solar thermal price is a key aspect to provide renewable heat supply, mostly because of low operation and maintenance costs and the large solar collectors’ lifetime. Martinopoulos and Tsalikis [31] developed a techno-economic model of a solar system for space and water heating of remote households in Greece. The model considered different collector sizes (from 8 to 12 m²) and storage tanks (from 0.5 to 0.65 m³). The results showed that it is possible to minimize the energy production costs with low payback periods and a positive net present value.

Optimizing the performance of energy systems through numerical models has been an effective option for researchers [5]. Some of those models are based on thermal–economic analysis that combines thermodynamic and economic principles to assess the costs of energy production of power plant components [32,33]. Karki et al. [6] presented a simplified model to assess a solar flat-plate collector energy system performance based on a modified f-chart implementation that accounts the amount of energy collected. The model also includes system cost determination. The model was tested considering various geographic locations and climate conditions. The model was implemented in MS Excel, resulting in a decision support tool that allows the collectors sizing for a specific solar fraction input. Cruz-Peragon et al. [34] proposed a model of a collector by applying a 2D finite-difference method with steady and transient conditions. The model is based on Newton’s method optimization to describe the critical coefficients of system, such as the emittance, plate absorbance, or convection transfer coefficient. Sharma and Diaz [35] developed a numerical model of a channel-based solar collector to evaluate thermal performance. The system was based on a flat-tube absorber enclosed with a coated glass envelope, which was used to minimize the convection losses. The steady-state model was evaluated in terms of collector efficiency. It was disclosed that the efficiency of the collector decreases with the increase in the inlet temperature because of the increase in radiative losses due to higher temperature reached at absorber surface. Similar research was conducted by Mansour [36] where the pressure drop and heat transfer inside the absorber channels were calculated by using Engineering Equation Solver EES software. Both studies have shown higher values in terms of collector efficiency with the inclusion of mini channels. Assaf and Shabani [17] presented a multi-objective optimization model of a solar–hydrogen combined heat and power system integrated with solar–thermal collectors to supply both power and hot water demand. Ust, Sahin, and Kodal [37] developed a thermo-economic analysis to maximize the power output per unit of the total cost. The model integrated physical and cost variables to optimize thermal and economic output. The costs integration is useful to disclose the most cost-effective configuration of the components and, then, improve the overall system design [38]. Lin et al. [19] applied a genetic algorithm to solar air systems to search for an optimal Pareto front of a multi-objective optimization problem. The system includes thermal energy storage using phase change materials in which the average heat transfer effectiveness and effective phase change materials charging time are defined as conflicting objective functions. Antoniadis and Martinopoulos [8] optimized a solar thermal system with storage with TRNSYS modeling software. The main objective was to assess the integration of different options of a solar collector array. The model calculates the annual domestic hot water and the space heating needs during the heating season for a typical single-family dwelling in the city of Thessaloniki (Greece). The system was optimized considering the collector area and the volume of the storage tank in order to optimize the use of the solar fraction. Yılmaz [39] proposed an original methodology for determining the optimum orientation and sizing of water-in-glass evacuated tube solar water heating systems for residential applications. The study was based on a transient model considering the system performance prediction for a year period through the System Advisor Model. Asadi et al. [40] presented multi-objective optimization of a 10 kW single-effect ammonia–water solar absorption cooling system. The model included an energy–exergy analysis, by assessing the effects of a different number of solar collector, as well as different solar collectors including a flat plate, evacuated tube, parabolic trough, and compound parabolic collectors. The system’s performance was studied for different ambient temperatures. None of these revised studies considers the cost of the individual components of the solar thermal system. Authors based their studies on the total costs of the systems and payback periods from the system investment.

In this work, a simplified model for a solar thermal system was formulated with the objective to minimize the investment costs while maximizing the solar collection efficiency. The mathematical model includes the definition of physical equations that describe the operation of the three main components: the solar collector that captures the solar radiation, the pump with its controller that promotes the forced convection of the heated water, and the storage tank, which is used to accumulate heat to be used when the radiation is not available. A set of cost equations was developed considering the most important physical variables and the cost coefficients were based on real data from commercial systems. The resulting thermo-economic optimization model was applied to supress the DHW needs of a typical residential building in Portugal.

2. Materials and Methods

This section presents the characterization of solar radiation and the solar availability at a specific region of Portugal, regarding the global horizontal radiation. The DHW for a typical residential building was also estimated considering the consumption of a family of four. Afterwards, we present the mathematical model for the energy and economic optimization of the solar thermal system.

2.1. Solar Radiation in Portugal

Portugal has excellent climate conditions to implement thermal systems based on solar energy. Solar radiation data in Portugal has been collected and analyzed by the IPMA—Instituto Português do Mar e da Atmosfera (Portuguese Institute for Sea and Atmosphere) [41]. The data were collected for a period corresponding to 15 years and, in order to ensure the quality data analysis, the data were presented as annual average Global Horizontal Irradiation (GHI) values (Figure 2) considering the following assumptions: (1) for days that lack more than two hours of data, the GHI was estimated through the mean daily value of the same period for the other years; (2) for days that lack less than two hours, the values for those gaps were interpolated from adjacent hours; (3) GHI annual variability was determined through the standard deviation of the annual averages of GHI (Figure 3).

The annual availability of GHI is higher in the South of Portugal. This is due to the more favorable atmospheric conditions, resulting in a high number of sunshine hours in that region. This evidence is confirmed by the annual variability in the availability of solar radiation, which is more reduced in these regions of the Portuguese territory. The greatest relative variability occurs mainly in the coastal regions and specific areas where cloud cover is highest. These areas coincide with the locations where the average GHI values are lower. Three different locations were selected to illustrate different GHI values and its variability (

Table 1. Annual average values of Global Horizontal Irradiation (GHI) and its variability for two different locations in Portugal.

Locations	GHI	GHI Variability
Guimarães (North)	1600 kWh/m2	3%
Lisbon (Centre)	1890 kWh/m2	4%
Faro (South)	1950 kWh/m2	2%

).

2.2. Typical DHW Consumption Profile of Portuguese Dwellings

In Portugal, a typical dwelling has an average occupation of 4 people, with a consumption of 40 L of water per person and per day. The DHW needs vary during the day, depending on the period of the time and building utility. Assuming the daily domestic hot water needs, it is possible to estimate the consumption demand (Cons_dhw in L/day). The thermal requirements for DHW (Q_DHW) can be calculated in accordance with the Portuguese regulation for the thermal behavior of buildings [42] as presented by Equation (1):

$$Q_{dhw}=Con{s}_{dhw}\times (4.187/3600)\times \Delta T\hspace{1em}\hspace{1em}\left(\mathrm{kWh}/\mathrm{day}\right)$$

(1)

where ΔT is the water temperature variation from the public water supply to the usage temperature. If not calculated, the public water supply temperature can be assumed with the reference value of 15 °C, whereas the usage temperature can be assumed to be 60 °C (ΔT = 45 °C). Thus, for a dwelling with a 160 L/day of DWH consumption, the yearly thermal requirements for DHW can reach 3056.5 kWh/year.

2.3. Solar Thermal System Description and Physical Model

The solar thermal system is composed by a flat-plate solar collector able to heat up a thermal fluid to a temperature plateau of 80 °C. A transparent glass cover is used to insulate the flat-plate collector and an absorber surface allows the conversion of solar radiation, which is transferred to the transport medium that circulates in the system tubes and is then pumped for further storage. The amount of solar radiation received by the collector is affected by the total radiation on a horizontal surface (I_g) and the collector surface area (A_solar). A fraction of the radiation is reflected, another portion is absorbed by the gazing cover, and the remaining radiation that penetrates the transparent cover is transferred to the absorber plate and absorbed by the collector [43]. Thus, the incident heat can be defined by Equation (2):

$$Q_i=I_g\times \tau \times \alpha \times A_{solar}$$

(2)

where τ is the collector aperture transmittance and $\alpha$ is the collector absorbance. Not all incident energy is absorbed by the panel. Part of the energy is reflected, and part of it is lost through conduction–convection [44,45]. As the collector absorbs heat, the temperature inside the collector rises, but some heat is lost by convection and radiation to the surroundings [25]. The heat loss ($Q_o$) depends on the collector overall heat transfer coefficient (U_L) and the temperature difference between the collector temperature ($T_c$) and the ambient temperature (T_a), as shown in Equation (3).

$$Q_0=U_L\times A_{solar}\times \left(T_c-T_a\right)$$

(3)

Thus, useful heat at the solar collector ($Q_c$) is then considered as the extraction heat at a steady-state condition. Therefore, this value is proportional to the useful heat that is absorbed by the solar collector as expressed by Equation (4):

$$Q_c=I_g\times \tau \cdot \sigma \times A_{solar}-U_L\times A_{solar}\left(T_c-T_a\right)$$

(4)

where σ represents the Stefan-Boltzmann constant (being σ equal to 5.6710⁻⁸ W/m².K⁴). The most important heat losses occur on the top surface of the solar collector through convection and radiation. It is generally assumed that about 80% of the solar radiation is adsorbed by the plate, but only 45% of the heat is collected by the collector tubes [44]. A simplified Sankey diagram of the heat flow at a standard flat-plate solar collector is shown in Figure 4. This output corresponds to average values reported in the literature, assuming that a fraction of the radiation is reflected back to the sky, another fraction is absorbed by the glazed cover, and the remaining is transmitted through the glass, reaching the absorber plate as short wave radiation [46,47,48].

When the temperature of the solar panel is equal to the ambient temperature, i.e., when there are no convective or radiative losses to the environment, the performance of the panel is equal to the optical performance. However, the efficiency of the solar collector can be estimated by knowing its efficiency if the fluid at the entrance was at ambient temperature and removing the heat losses. Thus, the solar collection efficiency is defined by the ratio between the received and the captured energy [2]. So, the solar collector efficiency (η_collection) can be estimated by Equation (5):

$${\eta }_{collection}=F\prime (\tau \alpha )-a_1\hspace{0.17em}T*-\hspace{0.17em}\hspace{0.17em}{a}_1{I}_g\hspace{0.17em}T{*}^2$$

(5)

where the variable T* is the maximum temperature that can be reached by the collector, considering certain solar irradiation and ambient temperature conditions. This term can be calculated as the ratio between the temperature gradient suffered by the thermal fluid with the irradiation $\left(T^{*}=T_f-T_a/I_g\right)$ in °C/(W/m²). The term F′ is defined as the irrigation factor, which is included in the equation as the correction factor. The linear losses coefficient is represented by $a_1$ = F′U_L. In fact, the heat transfer factor is defined as the ratio between the heat received by the fluid and the heat absorbed by the collector.

In other words, it is the fraction of energy that is provided by the solar heating system. This solar fraction must vary between 40 and 90%. Assessing the system operation based on the hourly model, and assuming that the energy needs and losses are constant throughout the day, the energy needs and the heat exchange can be defined as schematically represented by Figure 5. The distinct areas of the scheme (A to E) represent different points of operation of the solar thermal system between its start-up and shutdown period. When solar radiation is not enough to increase the thermal fluid temperature, and therefore trigger the solar thermal system, the necessary heat for the building appliances is supplied by the auxiliary backup system, typically a conventional boiler. The auxiliary backup system is used both at early and late hours of the day, when the solar thermal system no longer has the capacity to promote heat exchange (A region). During the solar collector starting-up (first hours of the day), the solar energy available is used to heat up the system due to the low temperatures reached during the night. This process occurs until the thermal fluid temperature is enough to transfer energy to the water (B region).

When solar energy is enough to increase the thermal fluid temperature, the necessary heat for the building appliances is supplied by the solar collector panel (C region) and the surplus is stored in the storage tank, which is represented by the positive heat variation (+ΔQ). The solar thermal system has a limited capacity to store the heat. From that point, all excess heat is dissipated (D region). Afterwards, when the heat captured by the solar panel is not enough to supply the useful energy requirements, the heat accumulated in the tank is then used to compensate for this difference (E region), which is represented by the negative heat variation (−ΔQ). By the end of the day, the collector stops capturing solar radiation (A region).

Thus, the collector selection is mainly based on the temperature to be obtained for the thermal fluid and its cost. The heat generated in the collectors is transported to the storage tank through the hydraulic circuit. This circuit includes pipes, connecting the collectors to the remaining components and promoting the thermal fluid circulation, which is most of the time guaranteed by the pump operation (forced circulation) [2]. The mass flow pumped in the primary circuit (${\dot{V}}_{pump}$) can be calculated as presented in Equation (6). This parameter mostly depends on the aperture area of the solar collector (A_solar) and the properties of the thermal fluid that is used in the system, such as density (ρ_tfluid) and the specific heat (c_p). Typically, this thermal fluid corresponds to a mixture of water with an appropriate concentration of antifreeze [15,18].

$${\dot{V}}_{pump}=\left(\frac{10F^{\prime }{U}_L}{c_p{}_{\hspace{0.17em}\hspace{0.17em}tfluid}}\times A_{solar}\times 3600\right)\times \frac{1}{{\rho }_{tfluid}}$$

(6)

Considering that the solar energy can be intermittent and it can be out of step with the hot water use, it is necessary to store the generated heat to be used when necessary. In order to avoid corrosion problems, most of the solar thermal systems use a storage tank with a heat exchanger, allowing the thermal fluid from the collector to circulate in the primary circuit and exchange heat with the secondary circuit (consumption circuit) [44]. Therefore, when choosing or sizing this component, a direct correlation can be established between the optimum volume (V_storage) of the deposit and the area of the solar collector (A_solar). According to [2], the optimal storage volume per unit of solar collection area is 0.070 m³/m². For values above 0.090 m³/m², the ratio between the efficiency of solar energy usage and the storage capacity do not lead to a greater use of incident solar energy; it only increases the storage tank volume and its cost [2,49]. This consideration can be translated into the model considering the upper and lower limit of the direct correlation between these two variables (Equation (7)).

$$V_{storage}={\lambda }_{storage}{A}_{solar}$$

(7)

According to [2], the optimal storage volume per unit of solar collection area, ${\lambda }_{storage}$ is 0.070 m³/m². Values above 0.080 m³/m² do not lead to a greater use of incident solar energy but only contribute to the increase in the storage tank volume and its cost [2].

2.4. Economic Model Definition

The costing methodology allows the costs to be defined in a transparent manner, so that options can be validated and compared equitably. Cost estimation of the investment associated with the implementation of a particular system requires gathering and validation of the cost data. For this, one can collect cost data from the literature and technology suppliers [49,50]. Defining the economic criteria for evaluating an investment while considering the system performance allows a cost-optimal level analysis of a thermal system [49,50,51].

In this study, a purchase cost equation was defined for each main component of the system: solar collector, storage tank, and circulation pump. The cost of each component depends on quality and size parameters in order to scale the thermal system sizing. The mathematical expressions were based on the incorporation of energy with cost variables, from which the cost estimation is performed to evaluate the system’s overall investment cost. The procedure uses the conventional chemical engineering methods for equipment sizing as well as the factorial method of cost estimation [52]. The coefficients of each cost equation were adjusted to the size of components, taking into account real market data, and the exponents were obtained by nonlinear regression. The costing methodology formulation, as well as each one of the cost equations, are briefly described because the complete model was already presented in previous works [49,53].

2.4.1. Solar Collector Cost Equation

The two most important physical variables that affect the solar collector (C_solar) cost are the collector area and the collection efficiency. Thus, the cost equation is given by Equation (8):

$$C_{solar}=C_{ref,solar}\times A_{ref,}{\hspace{0.17em}}_{solar}\times {\left(\frac{A_{solar}}{A_{ref,}{\hspace{0.17em}}_{solar}}\right)}^{b_{solar}}\times {\eta }_0^{\gamma }\times a_1^{\beta }$$

(8)

where C_{ref, solar} is the reference cost coefficient, A_{ref, solar} is the reference collector area, and A_solar represents the effective collector area. The equation also accounts the collector efficiency, which can be calculated as the product between the efficiency factor (η₀ = 0.789) and the linear loss coefficient (a₁). The exponents γ and β were estimated by nonlinear regression using the Advanced Process Monitor (APM) model in Matlab. The equation also includes a sizing factor (b_solar), which was estimated through the data collected from different commercial models with distinct specific costs and efficiencies [49].

2.4.2. Circulation Pump Cost Equation

The circulation pump (C_pump) cost equation was defined considering as the main sizing variable the water flow rate ($\dot{V}$_pump), as presented by Equation (9):

$$C_{pump}=C_{ref,pump}\times {\dot{V}}_{ref,pump}{\left(\frac{{\dot{V}}_{pump}}{{\dot{V}}_{ref,pump}}\right)}^{b_{pump}}$$

(9)

where the term C_{ref, pump} corresponds to the reference cost for this component, $\dot{V}$_{ref, pump} is the reference flow rate, $\dot{V}$_{f, pump} is the effective flow rate, and b_pump is the component sizing exponent.

2.4.3. Storage Tank Cost Equation

The storage volume (V_storage) is the key parameter that mostly affects the storage tank cost (C_storage). Nevertheless, the equation also includes the thermal insulation correction factor of the storage deposit ($In{s}_{storage}$), which is defined as a function of the insulation thickness and heat transfer coefficients based on data from commercial models. This term results from the calculation of the global heat transfer coefficient associated with the collector insulation layer$\left(In{s}_{storage}=1/U_S^{\delta }\right)$. Thus, the storage tank cost equality can be defined as presented by Equation (10):

$$C_{storage}=C_{ref,storage}\times V_{ref,storage}{\left(\frac{V_{storage}}{V_{ref,storage}}\right)}^{b_{storage}}\times In{s}_{storage}$$

(10)

where C_{ref, storage} refers to the reference cost coefficient, V_{ref, storage} corresponds to the reference storage volume, and b_storage is the sizing factor. All the reference coefficients were estimated considering the relative weight that it is attributed to each component in the final purchase cost of the solar thermal system. The sizing factors values were obtained after a sensitivity analysis, which was based on technical information from commercial systems [53]. The final values of the reference coefficients used in the economic model are presented in

Table 2. Reference coefficients assumed in the definition of cost equations.

Component	Parameter	Value
Solar collector	Reference cost coefficient, Cref, solar	298.5 €/m2
	Reference collector area, A ref, solar	2.50 m2
	Sizing factor, bsolar	0.5
Circulation Pump	Reference cost coefficient, Cref, pump	322.5 €/(m3.h)
	Reference flow rate, $\dot{V}$ref, pump	0.98 m3/h
	Sizing factor, bpump	0.3
Storage tank	Reference cost coefficient, Cref, storage	3647.5 €/m3
	Reference storage volume, Vref, storage	0.32 m3
	Sizing factor, bstorage	0.3
	Thermal insulation correction factor, $In{s}_{storage}$	0.985

.

3. Optimization Model

The studies available in the literature are mostly focused on the analysis of either a solar thermal system with a single fixed technology, where the goal is to optimize a single component and its operational conditions or find the best size for a specific application [9,12,54,55]. Multi-objective optimization has been defined as finding a vector of decision variables while minimizing or maximizing different objective functions, given several constraints [56].

3.1. Definition of Objective Function, Decision Variables and Constraints

In the present work, two objectives namely maximizing the solar collector efficiency, $Max f_1,$ and minimizing the annualized investment cost of the solar thermal system,$Min f_2$, are presented in Equation (11):

$$Objective\hspace{0.17em}functions\{\begin{array}{l}Maximize\hspace{1em}{f}_1\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{f}_1=-{\eta }_{collection}\\ \\ Minimize\hspace{1em}{f}_2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{f}_2=C_{inv}\times \left[\frac{i_e{(1+i_e)}^n}{{(1+i_e)}^n-1}\right]\end{array}$$

(11)

where $C_{inv}$ corresponds to the sum of three costs equations with the installation costs. The expenses with the installation costs (C_installation) typically represent a percentage of the investment with the solar collector panel (20% of the purchase cost). Thus, the total investment costs $C_{inv}$ can be estimated by Equation (12):

$$C_{inv}=\left(1.2C_{solar}+C_{pump}+C_{storage}\right).$$

(12)

In order to determine the equal amounts of annual cash flows of the investment, the $C_{inv}$ value is multiplied by the capital recovery factor, considering an effective rate of return, $i_e$, over n years of the solar thermal system operational time.

Three decision variables were selected for the numerical model: linear loss coefficient of the solar collector ($a_1$), the solar collection area (A_solar), and the tank storage volume (V_storage). Upper and lower bounds were defined in order to limit the so-called decision variable space. Those simple limits are presented by Equations (13)–(15).

$$3.5\le {\mathrm{a}}_1\le 5.8\hspace{1em}\left({\mathrm{W}/(\mathrm{m}}^2\mathrm{K})\right)$$

(13)

$$2.0\le A_{solar}\le 10.0\hspace{1em}\left({\mathrm{m}}^2\right)$$

(14)

$$0.060\le V_{Storage}\le 0.740\hspace{1em}\left({\mathrm{m}}^3\right)$$

(15)

The linear constraints were assumed in the model. These constraints aim to limit the operational parameters that give significance to the thermal model, including the guarantee that there is a temperature difference that promotes the heat transfer between the thermal fluid and the water (Equation (16)); the temperature limits for the thermal fluid should be limited considering their physical properties and guarantee the minimum temperature differential to promote the heat transfer process (Equation (17)).

$$T_f-T_a>10\hspace{1em}\left(°\mathrm{C}\right)$$

(16)

$$15<T_f<180\hspace{1em}\left(°\mathrm{C}\right)$$

(17)

3.2. Optimization Algorithm

Different algorithms can be used to solve constrained optimization engineering problems. Some methods are based on gradient calculations, whereas others are derivative-free methods, such as the search methods or the genetic and evolutionary algorithms [38]. The use of gradient-based methods requires that the objective function is a continuous and the derivatives exist. The derivative-free methods are suitable for solving optimization problems in practical contexts, with a considerable numbers of decision variables (less than 100) and without requiring a feasible initial solution or high computational effort [57,58,59].

Engineering problems have been solved by applying genetic algorithms [60,61]. While a classical algorithm generates a single optimal solution point at each iteration, a genetic algorithm generates a population of points, and the best point in the population approaches an optimal solution. It is a method for solving both constrained and unconstrained optimization problems based on a natural selection process that mimics biological evolution. The algorithm repeatedly modifies a population of individual solutions. At each step, the genetic algorithm randomly selects individuals from the current population and uses them as parents to produce the children for the next generation. Over successive generations, the population “evolves” toward an optimal solution. The population size depends on the nature of the problem but typically contains several hundreds or thousands of possible solutions. Usually, the population is generated randomly, allowing the entire range of possible solutions (the search space). The solutions may be “seeded” in areas where optimal solutions are likely to be found. A genetic algorithm requires a representation of the solution domain and a fitness function to evaluate it. The fitness function is a particular objective function that is used to give the merit of a given solution. After each simulation step, the worst solutions are excluded. Thus, fitness functions indicate how close a certain solution came to meeting the overall specification of the optimization problem. These algorithms are usually applied to find global minima for highly nonlinear problems [56].

Non-dominated Sorting Genetic Algorithm-II (NASGA-II) is a non-dominated and sorting-based multi-objective evolutionary algorithm used to solve problems that require constraint-handling [62]. This algorithm is a non-dominant and elitist genetic algorithm that picks individuals with better rank (fitness function value), which contributes to the population diversity [63]. This method has a reduced convergence time and it can handle mathematical models with nonlinear functions when compared with gradient-based methods [59]. The elitist selection mechanisms choose the best solutions of each generation without applying any operators. However, since a controlled elitist genetic process is used, the method allows a balance between the exploration and exploitation of the objective functions’ space and creates a feasible population regarding the defined linear constraints. Each solution is denoted by the vector of the decision variables. After the objective function and constraints evaluation, the obtained values for the population are scored through their comparison with the fitness function ones. The population and the offspring are combined into one matrix to extend the population, by computing the rank and crowding distance. In this study, a variant of NSGA-II was used as the optimization algorithm. The flow chart of the NSGA-II employment at MatLab is presented in Figure 6.

Then, the Pareto optimal solutions can be obtained, considering the trade-off between competing objectives. The optimization problem was solved with “gamultiobj” MatLab routine, considering a population size of 60 and a Pareto fraction of 0.35.

4. Results and Discussion

The numerical simulations were carried out considering a base-case scenario with a solar panel optimally oriented, 45° south, and set with an inclination of 51° angle. The thermal fluid was defined as a solution of water plus 22.5% of propilenoglycol (ρ_tfluid = 1190 kg/m³, c_p,_tfluid = 4.045 kJ/(kg.K)) [64]. For simulation purposes, it was assumed the same temperature at the absorbing plate and cover. Thus, the heat losses from the absorbing surface are assumed to be proportional to the gradient temperature between the absorbing surface and its surroundings.

The useful lifetime of solar thermal systems varies between 15 and 20 years [49]. For the base-case scenario, it was considered a period of 15 years.

4.1. Main Results

The optimization converged when the average change in the spread of Pareto solutions was lower than the minimum distance between objective function values. The objective function was evaluated a total of 29,881 times, and 497 generations were generated by minimizing the annualized investment cost and maximizing the solar collection efficiency. Figure 7 presents the multi-objective optimization results, which are expressed as a two-dimensional Pareto curve. Each point of the Pareto front represents the combination of the decision variables for which it is not possible to improve one of the objective functions without worsening the other one, accounting for the model constraints. This simulation was carried out considering the incident irradiation equal to 950 W/m² (base-case scenario).

Regarding the optimal solution space, the solar collection efficiency varies between 9.0% and 61.6%, and the annualized investment costs vary from 261.0 €/year to 358.24 €/year. From the analysis of the Pareto curve, it is shown that gains in overall efficiency above 60% result in a relative increase of about 16.3% in the annualized investment costs of the solar thermal system. On the other hand, for investments below 270 €/year in the system, the solar collector efficiency is extremely low (less than 50%). A possible explanation for these results might be related to the correctness of the sizing exponents of the solar collector, which should be adjusted after elaborating a more in-depth sensitivity analysis. Thus, based on the best trade-off between both objectives, an optimal solution point near 60% of efficiency and a system whose optimal physical solution allows an investment cost between 270 and 280 €/year should be selected.

The maximum and minimum value of the decision variables within the optimal frontiers in the objectives’ solution space is presented in

Table 3. Decision variables within the optimal frontiers in the objectives’ solution space.

Decision Variable	Minimum Value	Maximum Value
Solar collector linear coefficient loss, a1	3.684 W/m2.K	3.692 W/m2.K
Solar collector area, Asolar	4.00 m2	6.25 m2
Storage tank volume, Vstorage	0.203 m3	0.439 m3

. According to the results, the solar collector linear coefficient loss is a parameter that does not undergo a great variation. The optimal solar collector area value varies between 4.00 and 6.25 m². These results are in agreement with the literature because, according to [2], an equivalent area of 1 m² of solar panel is required to suppress, on average, a demand of 500 kWh/year. With these values, the solar thermal system is able to meet an annual thermal requirement varying between 2000 and 3120 kWh/year, which are within the DHW consumption of the typical Portuguese dwelling (estimated to reach a DHW thermal requirement of 3056.5 kWh).

Regarding the storage tank, the results depict a system with a volume between 0.203 m³ (203 L) and 0.439 m³ (439 L). This result shows that the storage volume per unit of solar collection area is within the expected values (0.07 m³/m²) for which the storage capacity is adjusted with the efficiency of solar energy usage [2].

The point on the Pareto front nearest to the equilibrium between the objectives is the “solution point” that considers the best trade-off between the objective functions. Thus, a point from the Pareto curve was selected in order to evaluate and analyze the physical and economic parameters for an optimal solution combination (

Table 4. Physical parameters of the “solution point” nearest to the trade-off equilibrium.

Physical Parameter	Value
Solar collector linear coefficient loss, a1	3.684 W/m2.K
Solar collector area, Asolar	4.17 m2
Storage tank volume, Vstorage	0.275 m3
Pump flow rate,$\dot{V}$pump	0.1364 m3/h

). We selected a point that corresponds to a panel with a solar area of 4.17 m² and a linear coefficient loss of 3.684 W/m².K, a storage volume of 0.275 m³, and a pump flow rate of 0.1364 m³/h. This combination allows obtaining a system with a solar collection efficiency of 61.2% and with an annualized investment cost of 283.3 €/year (for a system with 15 years of lifetime).

Considering the selected characteristics, the purchase cost of the thermal system components is presented in

Table 5. Purchase cost considering the optimal solution for the trade-off between objective functions and cost structure considering the relative share of each component.

Component	Purchase Cost	Relative Cost
Csolar	1059.6 €
Cstorage	1098.6 €
Cpump	174.9 €
Cinstallation	211.9 €
Total purchasing cost	2545.0 €

. The analysis shows that the solar collector and the storage tanks are the most expensive components of the solar thermal system, representing 42% and 43%, respectively. The installation costs represent about 8% of the system total cost, which corresponds to a value of 2545.0 €. The results show that for a solar–thermal system collector with 4.17 m², the system’s specific cost represents 610.3 €/m² of solar area. This value is relatively close to the commercial data, which ranges between 400 and 600 €/m² [49,65].

4.2. Sensitivity Analysis

As previously stated, the efficiency of a solar collector depends upon the irradiation, area exposed to solar radiation, wind velocity, diffuse particles in the atmosphere, fluid flow rate in the system, the material used in the absorber plate, and the heat transfer coefficient. However, one of the crucial parameters is the incident radiation, which affects the amount of energy that is transferred to the working fluid. It is desirable to make the difference between the absorbing surface temperature and the fluid as small as practicable in order to maximize the collection efficiency.

Thus, a sensitivity analysis was also performed in order to understand the influence of different solar irradiation values on the optimization model performance. The numerical simulations were carried out considering a lower and an upper value of incident radiation, 900 and 1000 W/m², as presented by Figure 8 and Figure 9, respectively. When comparing the Pareto fronts, the simulations disclosed an interesting trade-off between both objective functions. At higher values of irradiance (1000 W/m²), the solution space shows a set of optimal points with a lower dispersion of efficiency values for a more constrained variation of annualized investment costs. The solar collection efficiency varies between 62.8% and 73.2%, and the annualized investment costs vary from 272.4 €/year to 326.0 €/year. At lower values of irradiance (900 W/m²), the solar collection efficiency varies between 38.1% and 72.5% and the annualized investment costs vary from 265.5 to 350.6 €/year. The greater the incidence of radiation, the higher the collection efficiency of the panel, which requires smaller solar collecting areas, which reduces the investment cost for the system purchase. This outcome can be evaluated by estimating the annual investment cost for the optimal solution of storage tank volume and solar collector area values.

Two-dimensional contour maps (Figure 10) were generated to represent the annualized investment cost as a function of the storage tank volume and solar collector area, considering different values of incident radiation. The results were obtained by applying the Kriging method, which is an estimation technique that provides a minimum error-variance of the solution data.

5. Main Conclusions

In this paper, a multi-objective optimization model was applied to numerically simulate a solar thermal system. The mathematical modelling comprises the three main components: the solar collector that captures the solar radiation, the pump with its controller that promotes the forced convection of the heated water; and the storage tank, which is responsible for accumulating heat to be used when the radiation is not available. A set of cost equations was developed considering the most important physical variables, and the cost coefficients were based on real data from commercial systems. The resulting model was applied to supress the DHW needs of a typical residential building in Portugal. A typical dwelling with an occupation of four people has a daily consumption of about 160 L, which represents a DHW thermal requirement of 3056.5 kWh per year.

The costing methodology was defined considering the quality and sizing variables that most affect the cost of the system components. Regarding the solar collector, the solar area and the collecting efficiency are the most important physical parameters. The flow rate and the storage volume are the variables that affect the cost of the pump and storage tank, respectively. The coefficients of the cost equations were based on real data from commercial systems.

The multi-objective approach aimed to both minimize the system investment costs while maximizing the solar collection efficiency. The simulations were performed through a MatLab code by using an elitist variant of NASGA-II. The solar collection area and the linear loss coefficient as well as the tank storage volume were defined as decision variables. Upper and lower limits were attributed to the decision variables in order to give significance to the mathematical model. The numerical simulations were carried out considering that the solar panel was optimally oriented (45° south, with an inclination of 51° angle). The incident radiation was fixed with the value of 950 W/m².

The analysis of the Pareto curve led to the conclusion that a system with an annualized investment cost between 270 and 280 €/year allows reaching a collection efficiency of 60%. Considering the trade-off between the objective functions, a point from the Pareto curve was selected in order to evaluate the physical and economic parameters for an optimal solution: a panel with a solar area of 4.17 m² and with a linear coefficient loss of 3.684 W/m².K; a storage volume of 0.275 m³, and a pump flow rate of about 0.1364 m³/h. This combination allows obtaining a system with a solar collection efficiency of 61.2% and the acquisition of a system with an annualized investment cost of 283.3 €/year (for a system with 15 years of lifetime). For this optimal solution, the total purchasing cost is 2545.0 €, whereas the solar collector and the storage tank are the most expensive components, representing 42% and 43% of the investment costs, respectively. These results represents a specific cost of 610.3 €/m² per unit of solar collection area, which is relatively low when compared with the commercial data, which ranges between 400 and 600 €/m².

A sensitivity analysis was also performed in order to understand the influence of different solar irradiation values on the optimization model performance. Higher values of incident radiation result in systems that optimally have higher efficiencies, requiring smaller areas for solar collecting, which reduces the investment cost for the system purchase.

Regarding the manuscript limitations, a profile of solar radiation over the day should be added to the model in order to study more realistically the limitations of this type of renewable energy systems. Due to the intermittency of this energy source, it should also include the needs and costs regarding the backup system. As future work, it is intended to perform a sensitivity analysis in order understand the influence of systems lifetime and the interest rate in the annualized investment cost of the solar thermal system.