The Influence of an Interlayer on Dual Hydraulic Fractures Propagation

Abstract

Multi-cluster hydraulic fracturing of long-range horizontal wells is an approach for enhancing the productivity of low-permeability shale reservoirs. In this study, RFPA-Petrol (rock failure process analysis on petroleum problems) is applied for modeling hydraulic fracture propagation in multilayered formations. RFPA-Petrol based on coupled hydraulic-mechanical-damage (HMD) modeling was first tested by modeling a laboratory scale experiment on a physical (cement) model with a single completion. The modeling demonstrated the capability of RFPA-Petrol for simulating hydraulic fracture propagation. Then, we used RFPA-Petrol to investigate how the difference in material properties between oil-bearing layers and interlayers and the fracturing fluid properties influence the propagation of dual fractures in multilayered laboratory-scale models. In this case, the models with geological discontinuities in the vertical direction are strongly heterogeneous and RFPA-Petrol simulations successfully modeled the fracture configurations.

1. Introduction

Shale formations commonly consist of layered geological structures due to heterogeneous rock properties, in situ stress states, and interface properties [1,2,3,4]. Geological discontinuities in the vertical direction, such as weak interfaces and stress barriers, play a significant role in hydraulic fracture configuration, which is critical to the success of reservoir stimulation [5,6,7,8,9,10,11,12,13,14,15,16,17]. In this paper, if the Young’s modulus, strength, or Poisson’s ratio of the interlayer is larger than those of the adjacent oil-bearing layers, or the permeability of the interlayer is lower than that of the oil-bearing layers, the interlayer is called barrier, otherwise it is called weak layer. In field operations, weak layers, such as natural cracks and weak formation bedding planes, are beneficial in forming complex volume fractures. However, the existence of barriers has two sides. On the one hand, some barriers can separate a water saturated layer and an oil-bearing layer to avoid water flooding; on the other hand, some barriers exist in the middle of the two oil-bearing layers, which increase the difficulty of connecting the oil-bearing layers. The second case is usually improved by placing horizontal wells within the barrier between the upper and lower oil-bearing layers. However, it is hard to determine the exact vertical position of the horizontal well during operation. Its actual position sometimes is shallower or deeper than expected, resulting in that both oil-bearing layers are below or above the horizontal wellbore, and they may not be connected easily. Therefore, numerical simulations are conducted to investigate whether hydraulic fractures can cross the interlayer and connect the oil-bearing layers.

In the last five years, various numerical methods have been applied to simulate the propagation of vertical hydraulic fractures in multilayered formations. The most popular methods are the finite element method (FEM) [3,6,18,19,20,21], the distinct element method (DEM) [11,22,23], and the displacement discontinuity method (DDM) [1,2]. Finite element method is used in this research. However, most of the researchers utilize pseudo-3D models in FEM to predict hydraulic fracture propagation through heterogeneous layered formations [12,18,24,25,26,27,28,29]. In pseudo-3D models, each cross-section perpendicular to the main propagation direction is approximated as plane-strain, so that the 3D fracture problem is reduced to a 2D elastic deformation problem on the cross-section and a 1D lateral fluid flow problem [24,29]. The pseudo-3D model is faster but considers the vertical and horizontal propagation of the fractures separately [25]. As perforation technology is most commonly used in the stimulation of horizontal wells, the plain-strain assumption in the 2D or pseudo-3D model is unreasonable for perforations. In this paper, a real 3D hydraulic-mechanical-damage (HMD) model is used to investigate the intersection of dual hydraulic fractures with an interlayer. By using this approach, the stress distribution in the multilayered formations is calculated directly without defining high-stress zones or low-stress zones artificially. The HMD model is utilized in FEM based rock failure process analysis on petroleum problems (RFPA-Petrol) simulator [30,31]. The RFPA-Petrol considers that material heterogeneity causes macroscopic non-linear material behavior, which is essentially a representation of the accumulation of mesoscopic damage [30,31,32,33,34]. The mesoscopic elements have a binary logic state, which is damage state or non-damage (elastic) state [34]. By assuming that connected failed elements form fractures, there is no need to introduce additional crack elements [30]. RFPA-Petrol is suitable for simulation of 3D fracture propagation problems and costs lower computation time. The capabilities of RFPA family simulators related to hydraulic fracturing problems have been verified in multiple studies [35,36,37,38,39,40].

The geometry of hydraulic fractures growing in the vicinity of an interlayer is predominantly controlled by the difference in Young’s modulus, Poisson’s ratio, and permeability between the interlayer and oil-bearing layers [5,6,12,19,20,21,41,42,43]. When the material parameters of the layers are known, the fracturing fluid properties are of pivotal importance to propagation configuration. The scenarios of a single hydraulic fracture propagating near the interlayer have been studied and summarized by many authors [3,8,12,13,44,45,46,47,48,49,50,51]. Gu and Siebrits [12] mapped four possibilities of the interaction between a fracture and an interface: delamination, penetration, slippage, and bifurcation. Gu et al. [49] proposed that two outcomes (slippage, crossing) may occur when the hydraulic fracture reaches a natural fracture, and three outcomes (opening, crossing, branching) may occur thereafter. Wu and Olson [46], Pankaj [51], and Dahi Taleghani and Olson [47] addressed three scenarios for a hydro-fracture encountering a natural fracture: crossing, opening, and slippage. Guo et al. [3,13] suggested two types containing six potential forms of fracture geometry when propagating in layered reservoirs: penetrating the interface (crossing, opening, offsetting), and unable to cross (arresting, diversion, re-initiation). However, they did not take the thickness of the interlayer into consideration, and most of them just considered weak interlayers. Moreover, multi-cluster hydraulic fracturing is widely used in reservoir stimulation. Therefore, it is necessary to investigate the influence of interlayers containing weak layers and barriers on the propagation of dual fractures.

In this research, we used RFPA-Petrol to investigate how the difference in material properties between the oil-bearing layers and the interlayer and the fracturing fluid properties influence the propagation of dual fractures in multilayered laboratory-scale models. We also classified the interaction between dual fractures and interlayer into three types for both a weak layer and a barrier. Focusing on dual hydraulic fractures helps to understand the fracture propagation in multi-cluster fracturing, where the interaction of fractures must be considered. Besides weak layers, the study of barriers is indispensable and contributes to understanding horizontal well hydraulic fracturing of unconventional reservoirs where fractures usually meet barriers during propagation. Nevertheless, fluid properties are the artificially controlled factors affecting the intersection between hydraulic fractures and barriers in field-scale stimulation. Therefore, the above factors and situations are investigated in this research.

2. Methods

In the RFPA-Petrol, the elastic mechanics can be used to describe rock deformation at the elemental scale before damage [52]. Additionally, the coupled process is governed by Biot’s constitutive equation [53] as follows:

$$\mathsf{\sigma }=2G\mathsf{\epsilon }+\frac{2\nu G}{1-2\nu }tr\left(\mathsf{\epsilon }\right)I-\alpha pI.$$

(1)

Here, $\mathsf{\sigma }$ is stress tensor, $G$ is shear modulus, $\nu$ is Poisson’s ratio, $\mathsf{\epsilon }$ is strain tensor, $\alpha$ is coupling coefficient, and $p$ is pore-pressure.

Assuming elements with isotropic permeability and fluid flow governed by Darcy’s law, the fluid conductivity equation is written as [54]:

$$\frac{\rho g\kappa }{\mu }{\nabla }^{2}H-q=S\frac{\partial H}{\partial t}.$$

(2)

Note: that $\rho$ is the density of the fracturing fluid, $\mu$ is viscosity, $g$ is gravity, $q$ is volume sources, $\kappa$ is permeability, $H$ is water head, $t$ is time, and $S$ is specific storage [55].

In RFPA-Petrol, material parameters (such as Young’s modulus and strength) of the elements are assumed to follow a Weibull function with threshold values as [30,34,37]:

$$f\left(x\right)=\frac{m}{x_0}{\left(\frac{x}{x_0}\right)}^{m-1}\exp {\left(-\frac{x}{x_0}\right)}^m.$$

(3)

Here, $x$ is the microscopical mechanical parameters of the sample obtained from laboratory experiments, $x_0$ is the mean value of the elements put into numerical simulation program, exponent $m$ represents the degree of material homogeneity, $f\left(x\right)$ is the distribution density (MPa⁻¹) of material parameters $x$.

The mean Young’s modulus $E_0$ and strength ${\sigma }_{c0}$ of elements put into numerical simulation program can be approximately calculated by the following regression equations [56]:

$$\begin{array}{l}\frac{{\sigma }_c}{{\sigma }_{c0}}=\begin{array}{cc}0.2602\ln m+0.0233& \left(1.2\le m\le 50\right)\end{array}\\ \frac{E}{E_0}=\begin{array}{cc}0.1412\ln m+0.6476& \left(1.2\le m\le 10\right)\end{array}\end{array}.$$

(4)

The calculated value needs adjustments based on comparing the simulated stress–strain curve using these values with the laboratory one.

At the elemental scale, the rock mass is treated as an elastobrittle material with a residual strength [37]. Its mechanical behavior is modeled by an elastic damage constitutive law, and the residual strain/deformation upon unloading is not considered [37]. Mechanical damage of an element can be initiated based on the Mohr–Coulomb failure criterion combined with a maximum tensile strain criterion.

The damage variable of an element undergoing shear failure or tensile failure is expressed separately as follows [31,34,37]:

$$D=\{\begin{array}{cc}0& \begin{array}{cc}& {\epsilon }_1<{\epsilon }_{c0}\end{array}\\ 1-\frac{{\sigma }_{rc}}{{\epsilon }_1{E}_0}& \begin{array}{cc}& {\epsilon }_{c0}\le {\epsilon }_1\end{array}\end{array}.$$

(5)

$$D=\{\begin{array}{ccc}0& & \overline{\epsilon }>{\epsilon }_{t0}\\ 1-\frac{{\sigma }_{rt}}{\overline{\epsilon }{E}_0}& & {\epsilon }_{tu}<\overline{\epsilon }\le {\epsilon }_{t0}\\ 1& & \overline{\epsilon }\le {\epsilon }_{tu}\end{array}.$$

(6)

$${\epsilon }_{tu}=\eta {\epsilon }_{t0}.$$

(7)

Here, ${\sigma }_{rc}$ and ${\sigma }_{rt}$ is the residual compressive strength and the residual tensile strength,${\epsilon }_{c0}$ and ${\epsilon }_{t0}$ is the compressive strain at the elastic limit and the tensile strain at the elastic limit. ${\epsilon }_1$ is the maximum principal strain., ${\epsilon }_{tu}$ is the ultimate tensile strain of the element, $\eta$ is the ultimate strain coefficient, and $\overline{\epsilon }$ is the equivalent principal strain [57].

The hydraulic behavior responds to mechanics by permeability variation as Equation (8), i.e., the permeability of an element varies as a function of the effective stress state during elastic deformation [58,59,60], increases according to the cubic law when elements are damaged, and obey the assumption of pipe laminar flow for failure elements [31,37,61,62]:

$$\kappa =\{\begin{array}{ccc}{\kappa }_0{e}^{-b\left(\frac{{\sigma }_{ii}}{3}-\alpha P\right)}& & D=0\\ \frac{d_0{}^2}{12}& & 0<D<1\\ \frac{d_f{}^2}{32}& & D=1\end{array}.$$

(8)

Here, ${\kappa }_o$ is the initial permeability of the element, $b$ is the coupling coefficient, and ${\sigma }_{ii}/3$ is the average total stress. $d_o$ which is the distance between two parallel sides is equal to the hydraulic aperture of the element. Based on the assumption of confined-height fractures, $d_o$ could be calculated by $d_o\approx w=2p_{net}{h}_f\left(1-{\nu }^2\right)/E$, where $p_{net}$ is the net pressure and $h_f$ is the fracture height [63,64]. The equivalent diameter $d_f$ can be calculated by side length of the element by $d_f^2=4a^2/\pi$, where $a$ is the mesh size.

3. Validation

A numerical model with a single well was compared with the “single completion” laboratory test [65] to validate RFPA-Petrol’s ability to simulate fractures propagation process during hydraulic fracturing. The laboratory test block was 400 mm × 400 mm × 400 mm composed of off-white Portland cement and silica flour. It contained a 12 mm diameter wellbore, which left a small ‘open hole’ section at the bottom adjacent to a 40 mm diameter plastic disk constraining the fracture initiation location, as shown in Figure 1a,b [65]. The wellbore was oriented in the direction of the minimum stress imposed on the test block. The numerical model built in RFPA-Petrol was populated with a fine mesh discretization considering a distribution of material properties as shown in Figure 1c,d. The dimensions and parameters of the numerical model are shown in

Table 1. Material parameters and boundary conditions of the simulated “single completion” model in RFPA-Petrol.

Parameter	Symbol	Value 1	Unit
Young’s modulus	Em	7000	MPa
Uniaxial compressive strength	pm	35	MPa
Homogeneity index	m	4	-
Permeability	κ	8 × 10−20	m2
Poisson’s ratio	ν	0.20	-
Specific storage	Ss	1.38 × 10−6	m−1
Flux	Q	2.40 × 10−8	m3/s
Fracture fluid density	ρ	1000	kg/m3
Fracture fluid viscosity	μ	0.005	Pa·s
Maximum horizontal stress	σx, σH	6	MPa
Vertical stress	σy, σv	7	MPa
Minimum horizontal stress	σz, σh	5	MPa

¹ Values are obtained based on [31,65].

[31,65].

The numerical model had 1 million elements. The total number of steps was 100. The simulation costed 3 min per step with CPU computing. The simulated fracturing curve is shown in Figure 2 [65]. The pressure increases gradually in the first 290 s. Then, the pressure has a slower increase and reaches the peak value of 19.31 MPa at t = 350 s. After that, the curve declines slightly due to the increase of permeability and specific storage of damaged elements. The curve decreases sharply after shutting down the injection. At last, the pressure declines to about 10 MPa, which is higher than the laboratory extension stress possible due to an underestimation of volume storage in the fracture or propagation length. The initial pressurization of the borehole volume is highly non-linear in the experiment while linear in the model with a lower rate increase. The highly non-linear behavior in the experiment indicates non-linear fluid storage in the injection system, possibly due to an initial more compressible air in the system or non-linear compressibility due to different material components that is not considered in the numerical model.

The pressure when fracture initiated was lower than the break-down pressure. The initiation pressure was reached when the injection pressure-time derivative deviated significantly from a constant value [65]. Then, the pressure would increase for a short period and peaked at break-down pressure which refers to the maximum pressure sustained by the wellbore [65]. Fracture initiation pressure of the simulation was 17.96 MPa occurring at t = 290 s, and the relative error was 5%, while the simulated break-down pressure was 19.61 MPa when t = 350 s and the relative deviation was 0.6%.

Fracture propagation paths on the cross-section at y = 0.2 m are compared with paths gained from laboratory photographs as marked with black lines in Figure 3 [65]. This figure clearly shows the similarities and differences between laboratory results and numerical results. The fractured zone is oriented perpendicular to the direction of the minimum principal stress. The average simulated fracture radius is 150 mm by counting the hydraulic fractures where aperture was larger than 1.112 × 10⁻⁵ m. The relative error of the fracture radius is 11.7%. If the extent of fracture visible only under microscope is not considered, the relative error is 4.6%. The error is due to uncertainties regarding exact material strength properties, the modeling approach, and the experimental observations. Mean material strength properties of the numerical model are same as the laboratory model, but the local material properties and mineral distribution are different inducing the differences in fracture path and length. In this modeling approach, aperture reflects a hydraulic conducting aperture while mechanical aperture is translated to strain of the element thickness and tensile strain ahead of the fracture tip impacted by the size of the elements. Therefore, the stress concentration effect may be weaker than that in the laboratory test, and the fracture needs higher pressure to propagate. The experimental observations of the fracture propagation may be affected by the fact that the extent of fracture may only visible under a microscope.

Although there are some differences between the simulated results and laboratory observations, this validation demonstrates the capability of RFPA-Petrol simulator simulating of hydraulic-fracturing problems. The simulation can provide supplementary information on the stress distribution, pore-pressure distribution, and fracture aperture map that cannot be observed directly during laboratory tests.

4. Results and Discussion

4.1. The Impact of Interlayer Properties on Dual Hydraulic Fracture Propagation in Multilayered Laboratory-Scale Models

Numerical simulations are performed to investigate the influence of interlayer material parameters on dual hydraulic fracture configuration in a multilayered laboratory-scale model. The geometry, material properties of the simulated oil-bearing layer, and boundary conditions were derived from a laboratory ‘dual completion’ fracture test [65,66]. The model is 400 mm × 400 mm × 400 mm confined in a triaxial stress state where the principal stresses of 7 MPa vertical, 6 MPa maximum horizontal, and 5 MPa minimum horizontal stresses are applied as shown in Figure 4a,b. The initial fractures with a radius of 20 mm and separated by dx = 32 mm are oriented perpendicular to the direction of minimum horizontal stress. There is a 12 mm thick interlayer with different material properties defined in the lower third of the model. The interlayer is thin enough to investigate the intersections with hydraulic fractures. Moreover, the interlayer is defined just in the lower side of the model for comparing the propagation preference when the lower crack tip encounters the interlayer and the upper crack tip extends within the oil-bearing layer (from now on also denoted “oil-bearing layer”). There is no extra interface element between the interlayer and the oil-bearing layers. The slices of the model Multi-E1 built in RFPA-Petrol is shown in Figure 4c,d. In this model, the z-direction is the same as the vertical stress direction, and the x-direction is the minimum horizontal stress direction. The fracturing fluid density is 897 kg/m³, and its viscosity is 0.005 Pa·s. The injection rate is 1.10 × 10⁻⁸ m³/s.

Fifteen numerical experiment models are defined in addition to a control model (Multi-00) [31] which does not have an interlayer. The numerical experiment models are divided into 3 groups discussing the impact of Young’s modulus and strength, Poisson’s ratio, and permeability of interlayers on fracture geometry respectively. The material and seepage parameters of oil-bearing layers and interlayers of different models are listed in

Table 2. Material parameters of oil-bearing layers of the multilayered numerical model in RFPA-Petrol.

Parameter	Symbol	Value 1	Unit
Homogeneity index	m	4	-
Young’s modulus	Em	7000	MPa
Uniaxial compressive strength	pm	35	MPa
Poisson’s ratio	ν	0.20	-
Permeability	κ	8 × 10−20	m2
Specific storage	Ss	1.38 × 10−6	m−1

¹ Values are obtained based on [31,65,67].

and

Table 3. The material parameters of the interlayer in multilayered laboratory-scale models.

Model Number	Young’s modulus 1 (MPa)	Uniaxial Compressive 1 Strength (MPa)	Poisson’s Ratio	Permeability 1 (m2)
Multi-00	7000	35	0.20	8×10−20
Multi-E1	2100	11	0.20	8 × 10−20
Multi-E2	4200	21	0.20	8 × 10−20
Multi-E3	9800	49	0.20	8 × 10−20
Multi-E4	11,900	60	0.20	8 × 10−20
Multi-E5	14,000	70	0.20	8 × 10−20
Multi-Po1	7000	35	0.10	8 × 10−20
Multi-Po2	7000	35	0.15	8 × 10−20
Multi-Po3	7000	35	0.25	8 × 10−20
Multi-Po4	7000	35	0.30	8 × 10−20
Multi-Po5	7000	35	0.40	8 × 10−20
Multi-k1	7000	35	0.20	8 × 10−23
Multi-k2	7000	35	0.20	8 × 10−22
Multi-k3	7000	35	0.20	8 × 10−21
Multi-k4	7000	35	0.20	8 × 10−19
Multi-k5	7000	35	0.20	8 × 10−18

¹ Some of the values are obtained based on [67].

[31,65,67].

The fracture shape of the control model Multi-00 is shown in Figure 5. The geometry of dual fractures resembles an “x” shape without connection in the middle. Because of heterogeneity, the two initial fractures propagate successively. During hydraulic fracturing, the left fracture initiating first is called “primary fracture”, and the other fracture is called “secondary fracture”. The secondary fracture initiated after that the primary fracture has been propagating for some time, so its deflection is larger than that of the primary fracture. Since the breakdown moment is different in each model, the injection flux is kept constant in the simulation input even after the initiation of fractures to avoid variables induce by different shut-in time. However, this loading method results in the primary fracture continuing propagating and the secondary fracture not easily propagating in some models.

4.1.1. Sensitivity of Different Interface Young’s modulus and Strength

The impact of interlayer Young’s modulus and uniaxial compressive strength are discussed in this section. The ratio of the interlayer over oil-bearing layer Young’s modulus (and strength) ranges from 0.3 to 2.0. It is reasonable to vary these two parameters together because core samples drilled from an unconventional reservoir in China shows that uniaxial compressive strength has a positive correlation with the Young’s modulus [68].

Figure 6 shows the minimum compressive principal stress field of slice y = 0.2 m in models when t = 2000 s. By comparing the stress fields of these 6 models, it is found that Young’s modulus and strength of the interlayers play a key role in the final fracture configuration. When the Young’s modulus of the interlayer is much smaller than that of the oil-bearing layers, a distinct low-stress zone is observed in the interlayer. At the same time, the strength of the interlayer is much smaller than that of the oil-bearing layers, so fractures need lower fluid pressure to propagate in the weak interlayer than to penetrate through the weak layer. As shown in Figure 6a,b, both the primary fracture and secondary fracture of Multi-E1, and the secondary fracture of Multi-E2 turn to propagate parallel within the weak horizontal layer. Thus, the weak interlayer plays a guiding role in dual hydraulic fracturing. For Multi-E2, since the difference between the interlayer and the oil-bearing layers is not large enough, only the secondary fracture with relatively low fluid pressure inside the fracture is affected macroscopically. When the Young’s modulus of the interlayer is much larger than that of the oil-bearing layers, the minimum compressive principal stress in the interlayer is greater than that in the oil-bearing layers. At the same time, the interlayer has greater strength, so the fracture needs to accumulate higher fluid pressure to cross the interlayer. If the fluid pressure inside the fracture is not large enough for crossing the interlayer and beyond the extension stress of the oil-bearing layer, the fracture reoriented to propagate above the interlayer, such as the secondary fracture in Figure 6f. The stronger interlayer plays an arresting role in dual hydraulic fracturing. If the strength of the interlayer is not large enough to arrest the fracture, the fractures branch off above the interlayer, such as the secondary fracture in Figure 6e. When there is not many differences in Young’s modulus and strength of the layers, and the fluid pressure in the fracture grows quickly, the fractures extend along the initial orientation, such as both fractures in Figure 6d and the primary fracture in Figure 6e,f.

By comparing Multi-E1 and Multi-E5, although both models have transverse fractures, they have two significant differences. First, the vertical positions of fracture reorientation are different. The fractures in Multi-E1 turn into the weak interlayer and propagate along the bottom of the interlayer, while the secondary fracture in Multi-E5 tends to be reoriented parallel to the barrier and propagates above the barrier. Second, the zone between two fractures in the interlayer is damaged in Multi-E1, but not in Multi-E5. Because of the stress shadow effect, dual hydraulic fractures propagate away from each other. However, the zone between two fractures in the weak layer of Multi-E1 is damaged due to low strength.

Figure 7 shows how the upper and lower radius of primary fracture and secondary fracture change with the ratio of the interlayer over oil-bearing layer macroscopic strength [67]. It is found that the lower radius of primary fracture grows first and then declines with the increase of the ratio. It reaches its peak value at the ratio of 1. In other words, if an interlayer exists in the model, the lower radius of primary fracture decreases no matter if the interlayer is weaker or stronger than the oil-bearing layers. The upper radius of the primary fracture varies inversely with the lower one in general because when the lower fracture tip reaches the interlayer, it is influenced by the interlayer while fracture propagation continues at the upper part of the fracture. The first point in the primary fracture upper radius curve is an exception. As it is easier to propagate into the weak interlayer instead of propagating upward or downward at the ratio of 0.3, both the upper radius and lower radius of the primary fracture are smaller. By comparing the upper radius curves of primary fracture and secondary fracture, it is found that they have an opposite variation tendency which demonstrates the influence of the stress shadow effect. For the secondary fracture lower radius curve, since the lower secondary fractures in Multi-E1, Multi-E2, and Multi-E5 are reoriented parallel to the interlayers, their lower fracture radius is small. However, the secondary fractures in other models cross the interlayers, so their lower fracture radius is large.

The breakdown pressure (p_f) and time (t_f) of primary fracture and secondary fracture, and reopening pressure (p_r) and time (t_r) of primary fractures vary with the ratio of the interlayer over the oil-bearing layer macroscopic strength as shown in Figure 8. The breakdown pressure of primary fracture declines slightly with the increase of interlayer Young’s modulus and strength, as the interlayer Young’s modulus influences the stress distribution of the entire domain. The interlayers with smaller Young’s modulus will bear less compressive stress, while the strong interlayers will bear more. Therefore, interlayer with lower Young’s modulus results in higher in situ stress in the oil-bearing layers and the breakdown pressure of primary fracture increases. The variation tendency of the secondary fracture breakdown pressure is contrary to that of the primary fracture breakdown pressure, which reflects the impact of primary fracture on secondary fracture. The more easily the primary fracture propagate, the more significantly the primary fracture affects the secondary fracture. The secondary fracture needs a higher breakdown pressure when the interlayer has a large Young’s modulus, so the difference in breakdown pressure and time between primary fracture and secondary fracture increases with the increase of the ratio. In other words, the first peak of the primary and secondary pressure curves becomes further apart in peak magnitude and time to peak pressure. The reopening pressure of primary fracture fluctuates with the interlayer Young’s modulus.

4.1.2. Sensitivity of Different Interface Poisson’s Ratio

The impact of interlayer Poisson’s ratio on dual hydraulic fracture propagation is discussed in this section. The ratios of the interlayer over oil-bearing layer Poisson’s ratio are in the range of 0.5–2.0.

Figure 9 presents the minimum compressive principal stress field of models with different interlayer Poisson’s ratio at 2000 s. By comparing these six models, it is found that the difference in Poisson’s ratio influences the distribution of the minimum principal stress, but the hydraulic fracture paths do not change dramatically. The angle between the upper primary fracture and the vertical direction declines with the increased ratio in the models where the Poisson’s ratio of the interlayer is smaller than the value of the oil-bearing layers as shown in Figure 9a–c. The angle between the upper secondary fracture and the vertical direction declines with the increased Poisson’s ratio of the interlayers in the models where the interlayer has a larger Poisson’s ratio. When the Poisson’s ratio of the interlayer is large enough, secondary fractures have a short horizontal branch above the interlayer as shown in Figure 9e,f. However, the Poisson’s ratio has a narrow range and the strength difference of layers is not considered simultaneously, so it does not greatly affect the hydraulic fracture shape.

The upper radius and lower radius of primary fracture and secondary fracture in models with different ratios of interlayer over oil-bearing layer Poisson’s ratio at t = 2000 s are shown in Figure 10. It is found that the lower radius of primary fracture increases to 0.168 and remains constant when the ratio is between 0.75 and 1.25, then it decreases to the end of the curve. This plateau segment is due to that the fracture radius differences are less than 0.004 m, which is the statistic scale, cannot be acquired. From the general tendency of the primary fracture lower radius curve, it is seen that the interlayer with a higher Poisson’s ratio hinders the propagation of hydraulic fractures slightly. Unlike the tendency of the primary fracture lower radius curve, the upper one increases from the beginning to the end. When the ratio is less than 1, the curve increases due to the shrunken angle between the upper primary fracture and the vertical direction. When the ratio is larger than 1, the upper radius curve of primary fracture increases dramatically because the lower crack tip encounters the interlayer. By comparing the upper radius of the primary fracture and the secondary fracture, it is found that they have an inverse variation tendency except for an outlier. The secondary fracture geometry is influenced by both interlayer Poisson’s ratio and the primary fracture propagation. The primary propagation is the dominated factor in the upper part of the secondary fracture which is far away from the interlayer, while the interlayer Poisson’s ratio is the dominated factor for the lower part of the secondary fracture which is near the interlayer.

The breakdown pressure (p_f) and time (t_f) of the primary and secondary fractures, and reopening pressure (p_r) and time (t_r) of primary fractures vary with the interlayer Poisson’s ratio as shown in Figure 11. The variations of these six curves resemble that in Figure 8. The breakdown pressure of the primary fracture decreases slightly with the increase of the ratio of the interlayer over oil-bearing layer Poisson’s ratio. When the interlayer has a lower Poisson’s ratio, its minimum compressive stress is smaller while oil-bearing layer in situ stress is larger, so the breakdown pressure of the primary fracture is larger. On the other hand, the minimum compressive stress in the oil-bearing layer is smaller when the interlayer has a higher Poisson’s ratio, so the breakdown pressure of the primary fracture is smaller. As the primary fracture plays a key role in the initiation and propagation of secondary fracture, the breakdown pressure of secondary fracture increases gradually with the decrease of the primary fracture breakdown pressure. However, the curve of the primary fracture reopening pressure fluctuates irregularly, because the reopening pressure is influenced by the stress distribution indirectly which is a result of the interlayer Poisson’s ratio and is influenced by the interaction of crack tip and the interlayer directly.

4.1.3. Sensitivity of Different Interface Permeability

The impact of interlayer permeability on dual hydraulic fracture propagation is investigated in this section. As the difference in permeability of interlayer and oil-bearing layers differs by orders of magnitude in the field. Therefore, the ratios of the interlayer over the oil-bearing layer permeability are in the range of 10⁻³–10² in this research.

Figure 12 shows the seepage fields after 2000 s, for six different cases of interlayer permeability. As the permeability has a broad range and decides the distribution of fluid pressure directly, the interlayer permeability greatly affects fracture configuration. For the results in Figure 12a where the permeability of the interlayer is much smaller than that of the oil-bearing layers, the fracture fluid does not easily penetrate into the interlayer, and therefore the hydraulic fractures are arrested. When the permeability of the interlayer is smaller than the value of the oil-bearing layers, but is not small enough to arrest the hydraulic fractures, the fractures cross the interlayer (Figure 12b–e). After crossing the interlayer, the fluid pressure declines, the fracture aperture narrows or the fracture length shortens, which illustrates that the interlayer impedes fluid flow. When the permeability of interlayer is much greater than the value of the oil-bearing layers, fluid flows easily into the interlayer, so the fluid pressure in the interlayer increases rapidly, and the interlayer is easy to crack (Figure 12f). When the permeability of the interlayer is a bit greater than the value of the oil-bearing layers as shown in Figure 12e, dual hydraulic fractures extend in the original orientation, but the seepage area in the interlayer is larger than that of the oil-bearing layer.

The upper radius and lower radius of the primary fracture and secondary fracture in models with different ratios of interlayer over oil-bearing layer permeability at t = 2000 s are shown in Figure 13 [67]. By comparing the upper and lower radius of the primary fracture, it is found that the lower radius of the primary fracture increases first then decreases, while the tendency of its upper radius curve is on the contrary. When the interlayer permeability is the same as the oil-bearing layer value, the primary fracture gains its longest lower radius and shortest upper radius. It shows that the interlayer permeability is a predominant factor affecting dual hydraulic fracture radius. A lower interlayer permeability inhibits the propagation of lower primary fracture and induces the upper primary fracture extending more easily. For the case of a high permeability interlayer, the hydraulic fracture entering the interlayer tends to be reoriented perpendicular to the vertical stress, which is relatively high, leading to higher stress normal to the hydraulic fracture. As a result of the higher stress, further fracture propagation is embedded in the interlayer, while fracture radius can increase in the upper part of the fracture. By comparing the upper radius curves of primary fracture and secondary fracture, they have opposite tendencies reflecting the influence of the primary fracture on the secondary fracture. The primary fracture may restrain the secondary fracture from extending or cause the deflection of secondary fracture. As the primary fracture propagates first without the initiation of secondary fracture, the primary fracture is influenced by the interlayer permeability directly. On the other hand, the secondary fracture initiates under the presence of the primary fracture, so its configuration is affected by both interlayer permeability and the propagation of primary fracture. Therefore, the secondary fracture radius does not vary systematically with the ratio of the interlayer over oil-bearing layer permeability. However, it can be found that when the permeability of the interlayer and the oil-bearing layers are the same, the lower radius of the secondary fracture is the largest, and the difference in permeability of the interlayer and the oil-bearing layers cause the reduction of the lower secondary fracture radius.

The breakdown pressure (p_f) and time (t_f) of primary fracture and secondary fracture, and reopening pressure (p_r) and time (t_r) of primary fractures vary with the ratio of interlayer over oil-bearing layer permeability as shown in Figure 14. The two breakdown pressure curves and two breakdown time curves are constant because the permeability of the interlayer does not influence the in situ stress distribution before fracture initiation. However, the reopening pressure of the primary fracture is affected by the interlayer permeability because the primary fracture has reached the interlayer before the secondary fracture reopening. The reopening pressure decreases and then increases with the increase of the ratio. The lowest value of reopening pressure occurs when the interlayer and oil-bearing layers have the same permeability, which means that the primary fracture reopens most easily under this condition.

In summary, the RFPA-Petrol was used to investigate the influence of the interlayer with different hydraulic and mechanical properties on the propagation of dual hydraulic fractures in a multilayered laboratory-scale model. It is found that the difference in mechanical parameters of the interlayer and the oil-bearing layers influence the hydraulic fracture geometry and breakdown pressure while the difference in permeability only influences the fracture geometry. When the interlayer is much weaker than the oil-bearing layers, the hydraulic fractures turn to propagate parallel within the weak horizontal layer. When the interlayer is much stronger than the oil-bearing layers, the fracture is reoriented to propagate above the interlayer. Moreover, the interlayer with higher Poisson’s ratio hinders the propagation of hydraulic fractures slightly. The breakdown pressure of the primary fracture declines and the breakdown pressure of the secondary fracture increases with the increase of interlayer Young’s modulus or Poisson’s ratio. When the interlayer has sufficient high permeability, the dual fractures turn into the interlayer. Otherwise, the hydraulic fracture is arrested by the interlayer with low permeability. In most cases, interlayer with high Young’s modulus has a low permeability, so the barriers always hinder the propagation of fractures.

4.2. The Impact of Fracturing Fluid Parameters on the Propagation of Dual Hydraulic Fractures in a Multilayered Laboratory-Scale Model

In field scale stimulations, the material properties are given and fixed by nature. Therefore, changing fluid properties is one of the most useful ways to control the intersection between hydraulic fractures and barriers. The influences of fracturing fluid flux and viscosity on dual hydraulic fracture propagation are investigated in this section. The different parameters of the barrier and oil-bearing layers are listed in

Table 4. Material parameters of the barrier and the oil-bearing layers in the multilayered numerical model in RFPA-Petrol.

Parameter	Symbol	Oil-Bearing Layer Value	Barrier Value	Unit
Macroscopic Young’s modulus	Em	7000	14,000	MPa
Macroscopic strength	pm	35	70	MPa
Poisson’s ratio	ν	0.20	0.25	-
Permeability	κ	8 × 10−20	4 × 10−21	m2

. Other boundary conditions and material parameters are the same as those used in Section 4. The model configuration is the same as models in Figure 4a,b as shown in Figure 15. There are 10 numerical experiment models which are divided into 2 groups in addition to a control model (Multi-01). The parameters of fracturing fluid of different models are listed in

Table 5. The flux and viscosity of the fracturing fluid in multilayered laboratory-scale models.

Model Number	Flux (m3/s)	Viscosity (Pa·s)
Multi-01	1.13 × 10−10	0.005
Multi-Q1	5.60 × 10−11	0.005
Multi-Q2	8.40 × 10−11	0.005
Multi-Q3	1.40 × 10−10	0.005
Multi-Q4	1.96 × 10−10	0.005
Multi-Q5	2.25 × 10−10	0.005
Multi-vis1	1.13 × 10−10	0.001
Multi-vis2	1.13 × 10−10	0.0025
Multi-vis3	1.13 × 10−10	0.075
Multi-vis4	1.13 × 10−10	0.01
Multi-vis5	1.13 × 10−10	0.02

.

4.2.1. Sensitivity of Different Flux

The impact of inlet flux (injection rate) on dual hydraulic fracture propagation in multilayered models is presented in this section. The ratio of the numerical experiment model over the control model flux ranges from 0.5 to 2.0 in this research.

Since the variable is flux, it is unreasonable to compare models at the same moment. The seepage fields of models when their primary fractures reach the upper boundary are in comparison as shown in Figure 16. The fractures in the six models are reoriented to propagate or brach off above the interlayer. The left and right horizontal fractures do not connect and propagate away from each other due to the stress shadow effect. By comparing the six models, the secondary fracture length increases with the increase of flux. When the flux is smallest as shown in Figure 16a, the secondary fracture cannot propagate efficiently and merges into the primary fracture. Whereas, for Figure 16f where the flux is the largest, parts of the dual fractures cross the barrier and form branches, the main part of the fractures turn to propagate in the horizontal direction above the barrier. The angles between the vertical fracture braches and the vertical direction are smaller than the angles before crossing the barrier. When the flux is not large enough to cross the barrier as shown in Figure 16e, the primary fracture and secondary fracture mainly propagate above the barrier, but the fractures may find a weak element to penetrate the barrier as material heterogeneity is considered in the simulation. Due to the stress shadow effect, the lower parts of the dual fractures in every model propagate away from each other, and the zones between them are not damaged.

The upper radius and lower radius of the primary and secondary fractures in models with different flux ratios are shown in Figure 17. The upper radius curve of the primary fracture is a horizontal line because of the choice of the special statistical moment. The upper radius of the secondary fracture increases with the increase of the inlet flux, which is consistent with the seepage field diagrams. Because the larger the inlet flux is, the faster the fluid pressure in the secondary fracture increases after the initiation of the primary fracture, the easier it is to crack. The upper radius of the secondary fracture at the ratio of 0.5 deviates from the curve, mainly because of the upper part of the secondary fracture merging into the primary fracture. The lower radius of the secondary fracture rises except for the segment between the ratio of 1.0 and 1.25. By comparing the upper radius curve and the lower one of the secondary fracture, it is found that there is a point of intersection when the ratio of flux equals 1.1. Before this point, the flux is small and the secondary fracture barely crosses the barrier, so the upper radius of the secondary fracture is larger than the lower one. After the intersection point, partial fluid penetrates the barrier, so the lower radius increases beyond the upper radius.

The breakdown pressure (p_f) and time (t_f) of the primary and secondary fractures, and the reopening pressure (p_r) and time (t_r) of the primary fracture vary with different flux as shown in Figure 18. The breakdown and reopening pressures of the primary fracture increase significantly with the increase of the flux. This increase in breakdown and reopening pressures occurs possibly because the breakdown pressure depends on pressure diffusion near and ahead of the fracture tip. A quicker loading implies that there is not time enough for the fluid pressure to penetrate as much and therefore higher pressure is required to extend the fracture. This may also be affected by the mesh size especially at the highest injection rate and quickest loading. Figure 18 shows that the breakdown pressure of the secondary fracture decreases first and then increases with increasing flux. The difference between the primary fracture breakdown time and the secondary fracture breakdown time declines gradually. When the flux ratio is less than 1, the breakdown time of the secondary fracture occurs much later than that of the primary fracture, so the secondary fracture cannot extend efficiently. When the ratio is larger than 1, the fluid pressure inside the secondary fracture increases rapidly, so its initiation follows the breakdown of the primary fracture.

4.2.2. Sensitivity of Different Fluid Viscosity

The impact of fluid viscosity on dual hydraulic fracture propagation in multilayered models is investigated in this section. The ratios of the numerical experiment models over the control model fracturing fluid viscosity are in the range of 0.2–6.0 in this research.

The seepage fields of models with different fluid viscosity are shown in Figure 19. The fluid viscosity is one of the major factors influencing the dual fracture propagation. By comparing the six models, it is found that lower viscosity fluid has a better fluidity, inducing a faster growth of the primary fracture length which reaches the upper boundary in a shorter time. Whereas, higher viscosity fluid has a lower filtration and benefits the formation of the wide primary fracture, but it leads to the primary fracture length increasing more slowly. Then, we discuss the impact of fluid viscosity on whether the hydraulic fractures cross the barrier. When the fluid viscosity is low, both the primary and secondary fractures are hindered by the barrier as Figure 19a,b. In Multi-vis1 and Multi-vis2, the primary fractures initiate first, they continuously extend as the fluid pressure is concentrated at the crack tip. The secondary fractures do not initiate until the lower primary fracture tips reach the barrier or the upper primary fracture tips reach the boundary. Then, the secondary fractures merge into the primary fractures finally. When the fluid viscosity is large enough as shown in Figure 19d–f, the primary fractures penetrate the barrier and branch off above the barrier, but the length of secondary fractures is short. If the injection of the primary fracture is shut down after its propagation, the secondary fracture may propagate more sufficiently.

The upper radius and lower radius curves of primary fracture and secondary fracture in models with different ratios of the numerical experiment model over the control model fluid viscosity at the moment of primary fracture reaching the upper boundary are shown in Figure 20. The lower radius of the primary fracture changes in a wide range especially during the ratio of 0.5 to 2. After this range, the lower radius of the primary fracture becomes stable and changes slightly. When the fluid viscosity is high, fluid pressure is concentrated near the initial perforations. The fluid pressure inside the primary fractures does not drop after initiation, so the primary fracture keeps propagating and crosses the barrier. The shape of the upper radius curve and lower radius curve of the secondary fracture are similar because the secondary fractures, which nearly do not encounter the barrier, are predominantly controlled by the primary fracture resulting in short secondary fractures. The secondary fractures show longitudinal symmetry when the ratio is larger than 1.0.

The breakdown pressure (p_f) and time (t_f) of the primary and secondary fractures, and reopening pressure (p_r) and time (t_r) of primary fractures vary with different viscosity, and are shown in Figure 21. The breakdown pressure and reopening pressure of the primary fracture increase with the increase of the viscosity. As the lower viscosity fracturing fluid leads to higher fluid conductivity, the pore pressure near the initial perforations is higher which results in a lower breakdown pressure in the primary fracture. It is found that the value of the primary fracture reopening pressure approaches the value of the primary breakdown pressure gradually and exceeds the breakdown pressure after the ratio of 4. It inflects that the fluid pressure inside the primary fracture declines less when the viscosity is higher, even increases when the viscosity is the largest. When the ratio equals 0.2, the breakdown pressure of the secondary fracture nearly equals the breakdown pressure of the primary, as the secondary fracture initiates when the crack tips far away from the initial fractures. The breakdown pressure of the secondary fracture decreases after the ratio of 0.5. The breakdown of the primary fracture becomes later when the viscosity is higher. The time difference between the reopening and breakdown of the primary fracture decreases with the increase of fluid viscosity after the ratio of 1.

5. Conclusions

In this research, it is found that the mechanical properties and permeability of the interlayer greatly affect the fractures configuration. The fluid flux and viscosity are also major factors. Moreover, the dual fractures influence each other during the stimulation. We classified the interaction between dual fractures and interlayer into three types (crossing, branching, and drainage or arresting) for both a weak layer and a barrier. They can be further subdivided into sixteen patterns. The detailed conclusions are as follows:

• When the mechanical properties of the interlayer are different from those of the oil-bearing layers, the interlayer has an indirect effect on the dual fractures by influencing the in situ stress distribution and has a direct influence by arresting or guiding the propagation of dual fractures.
• When the permeability of the interlayer is different from those of the oil-bearing layers, the stress field will not be affected, but since the permeability changes in a range of several orders of magnitude, the permeability of the interlayer plays a key role on the dual fractures configuration and the reopening pressure of the secondary fracture.
• The propagation of the secondary fracture is affected by both of the primary fracture and the interlayer. The primary fracture plays a major role in the growth of the upper part of the secondary fracture, which is far from the interlayer, while the lower part of the secondary fracture near the interlayer is predominantly controlled by the interlayer.
• When the properties of the interface are known, increasing the fracturing fluid flux is beneficial in the dual fractures crossing the interlayer. However, the fractures have branches in the horizontal direction above the interlayer, so the fluid volume is reduced after penetrating the interlayer.
• When the properties of the interface are known, increasing the fracturing fluid viscosity makes it easier for the primary fracture to cross the interlayer. Under hydraulic fracturing with a high viscosity fluid, if we shut down the injection after the initiation of the primary fracture and reopen it after the initiation of the secondary fracture, both two fractures may penetrate the interlayer.
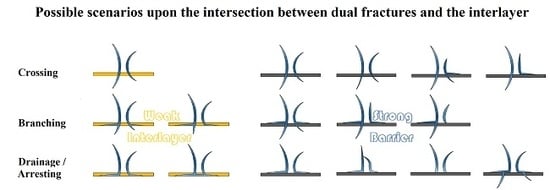
• In this paper, the interaction between dual fractures and interlayer are classified into three types for both weak layer and barrier by the primary fracture geometry as shown in

  Table 6. Possible scenarios upon the intersection between dual fractures and the interlayer.

  No.	Type Name	Pattern Sketch
  		Intersection with a Weak Layer		Intersection with a Barrier
  1	Crossing
  2	Branching
  3	Drainage/Arresting

  . For intersection with a weak layer, the three types are:
  • dual fractures cross the weak layer;
  • the primary fracture branches off into the weak layer, including two patterns: (a) both fractures branch, (b) the primary fracture branches while the secondary fracture turns into the weak layer;
  • dual fractures turn to propagate parallel within the bottom of weak layer, including two patterns: (a) dual fractures propagate away from each other in the weak layer without a fractured zone between them, (b) dual fractures are reoriented into the weak layer and merge into a large horizontal fractured domain.
  For intersection with a barrier, the three types are:
  • the primary fracture crosses the barrier, including four patterns: (a) dual fractures penetrate the barrier without changing in width, (b) dual fractures penetrate the barrier with a width narrowed, (c) the primary fracture penetrates the barrier while the secondary fracture branches off above the barrier, (d) the primary fracture penetrates the barrier while the secondary fracture is reoriented to propagate parallel above the barrier.
  • the primary fracture branches off above the barrier, including three patterns: (a) dual fractures branches off above the barrier, (b) the primary fracture branches off above the barrier while the secondary fracture is reoriented to propagate parallel above the barrier, (c) the primary fracture branches off above the barrier while the secondary fracture is stopped by the barrier.
  • the primary fracture is arrested by the barrier, including four patterns: (a) lower parts of the dual fractures are reoriented to propagate parallel above the barrier and the upper parts of them propagate away from each other, (b) lower parts of the dual fractures reoriented to propagate parallel above the barrier and the upper part of the secondary fracture merges into the primary fracture, (c) both of the fractures are stopped by the barrier, (d) dual fractures are reoriented into the barrier and find a weak place to penetrate the barrier. Table 6 contains most of the fracture configuration when dual fractures encounter an interface.