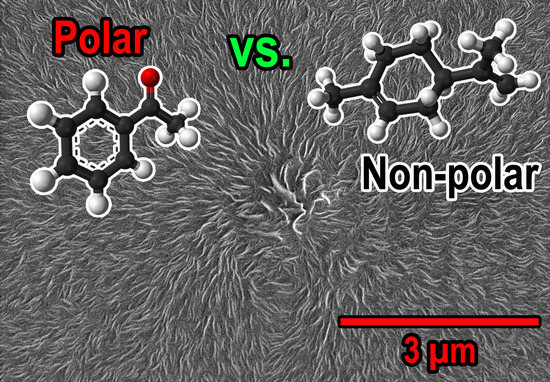
Solubility and Diffusivity of Polar and Non-Polar Molecules in Polyethylene-Aluminum Oxide Nanocomposites for HVDC Applications

Abstract

The best commercial high-voltage insulation material of today is (crosslinked) ultra-pure low-density polyethylene (LDPE). A 100-fold decrease in electrical conductivity can be achieved by adding 1–3 wt.% of well-dispersed inorganic nanoparticles to the LDPE. One hypothesis is that the nanoparticle surfaces attract ions and polar molecules, thereby cleaning the surrounding polymer, and thus reducing the conductivity. LDPE-based nanocomposites with 1–12 wt.% octyl-coated aluminum oxide nanoparticles were prepared and the sorption and desorption of one polar compound (acetophenone, a crosslinking by-product) and one non-polar compound of a similar size (limonene) were examined. Since the uptake of acetophenone increased linearly with increasing filler content, whereas the uptake of limonene decreased, the surface attraction hypothesis was strengthened. The analytical functions for predicting composite solubility as a function of particle size and filler fraction were derived using experimental solubility measurements and Monte Carlo simulations.

1. Introduction

In order to transport renewable electrical energy across continents with tolerably low energy losses, the voltage levels for the next generation of high-voltage direct-current (HVDC) cables must increase from today’s 640 kV to 1–2 MV. To achieve this voltage increase, improved insulation materials must be developed. Ultrapure low-density polyethylene (LDPE) has a low electrical conductivity and is, therefore, the dominating HVDC insulating material today. A higher thermal stability is achieved by crosslinking the polyethylene (XLPE), but chemical crosslinking with peroxides produces polar species (e.g., acetophenone, cumyl alcohol) which increase the electrical conductivity. For instance, a five-fold conductivity increase was observed for (non-degased) XLPE, compared to the corresponding LDPE, when measured at 60 kV/mm, 20 °C and 6 h [1]. This unwanted effect can be reduced by minimizing the initial peroxide concentration and by degassing the XLPE after the reaction [2,3]. After careful degasing, the difference in conductivity between XLPE and LDPE approaches zero [1,4], but the degasing process is generally time- and energy-consuming and thus is not ideal for the environment. Two main strategies for reducing the electrical conductivity of the polyethylene have been proposed, either blending small fractions of high density polyethylene (HDPE) with the LDPE [4] or dispersing small fractions (1–3 wt.%) of metal oxide nanoparticles (e.g., Al₂O₃, MgO and ZnO) in the LDPE [5,6,7,8,9]. The nanocomposite strategy gives a larger reduction in electrical conductivity (~30 times for 3 wt.% Al₂O₃ at 32.5 kV/mm, 60 °C, 11 h, Figure 1 [7]), but the physical mechanism behind the conductivity improvement and the reason for the local optimum, around 3 wt.% nanoparticles, is still under debate.

One hypothesis for the conductivity reduction in nanocomposites is that electrons and holes are trapped in deep traps in the nanoparticle surface [10,11,12,13]. A complementary hypothesis is that ions and molecules with permanent dipole moments, such as water and crosslinking by-products, are also attracted and adsorbed onto the nanoparticles, resulting in the cleaning of the polyethylene matrix [9,14]. Liu et al. (2016) [14] reported that nanoparticles (Al₂O₃, MgO and ZnO) suspended in (hydrophobic) heptane can adsorb polar molecules (water, dicumyl peroxide, acetophenone and cumyl alcohol) and that selective adsorption can be achieved by coating the nanoparticle surface. The surface coating could be tailored to adsorb small, undesired impurities, such as acetophenone, but not the larger antioxidants. Nilsson et al. (2017) [8] reported that the water solubility of MgO/LDPE nanocomposites increased significantly with increasing MgO filler content and utilized Finite Element Modeling (FEM) to predict how the increased solubility would affect the electrical conductivity. A minimum of conductivity was predicted at around 3 wt.%, because at higher filler fractions, the particles can both agglomerate and form conductive paths through the material. Conductivity measurements confirmed the FEM predictions. At a low relative humidity (RH) (~0%), the conductivity was lowest in the presence of 1–3 wt.% nanoparticles, but at a high RH (~50%), pure polyethylene (PE) had the lowest conductivity.

A low electrical conductivity is a necessary condition for a good HVDC insulator material, but several other electrical and mechanical properties are also of importance. Fortunately, PE/Al₂O₃ nanocomposites typically have improved properties when compared to pure PE, including a reduced space charge accumulation [15,16,17,18] dielectric permittivity [19,20] and thermal conductivity [12]. Additionally, an increased elastic modulus [21,22], tensile strength [23] thermal stability [22] and dielectric breakdown strength [15,16,17,24] has been reported. Good reviews on nanocomposites for electrical applications include [6,25,26,27,28,29,30,31].

In this study, the sorption and desorption of penetrant molecules in non-crosslinked LDPE-Al₂O₃ nanocomposites were examined to test the hypothesis that the nanoparticles attract polar molecules and clean the surrounding polyethylene polymer matrix. The transport performance of acetophenone (the polar compound) and limonene (the non-polar compound) was, therefore, assessed. Acetophenone (C₆H₅COCH₃), which is an LDPE crosslinking by-product, was chosen because of its undesired presence in today’s commercial HVDC insulation materials. Limonene (C₁₀H₁₆) was chosen because of its distinct non-polar character, with octanol/water partition coefficient log (K_ow) = 4.57 [32] when compared to 1.58 [33] for acetophenone. Since the chemical structures and molar masses of limonene (136 g/mol) and acetophenone (120 g/mol) were comparable, the influence of polarity on diffusivity and solubility was expected to be comparatively easy to isolate.

2. Material and Methods

2.1. Material Preparation (LDPE and LDPE/Al₂O₃ Nanocomposites)

The polyethylene plates were produced by the extrusion and compression molding of LDPE pellets (M_w: 75 kDa [7], Borealis AB (Stenungsund, Sweden)). The LDPE pellets were first immersed in liquid nitrogen for 1 h and then cryo-ground into powder. Subsequently, the powder was mixed with n-heptane. After 12 h drying in air at 80 °C, the LDPE powder was processed (6 min, 150 °C, 100 rpm) in a mini-extruder (Micro 5cc Twin Screw Compounder, DSM Xplore). The extruded rods were vacuum dried (80 °C, 12 h), pelletized and compression molded (LabPro 400 Press, Frontlijne Grotnes (Niles, MI, USA)) at 130 °C into 300 µm hick plaques. Polyethylene terephthalate (PET) films were used as anti-sticking layers between the metal press plates and the LDPE. During the compression molding, a contact pressure was first applied (5–8 kN, 10 min, ramping to 130 °C), followed by compression (200 kN, 10 min, 130 °C) and, finally, cooling back to room temperature (200 kN, 7 min) [34]. Reference samples were also produced by compression molding the virgin (non-extruded) LDPE pellets.

The corresponding LDPE-Al₂O₃ nanocomposite plates were made with the same protocol, with the only difference being that 1–12 wt.% Al₂O₃ nanoparticles were added to the LDPE matrix before extrusion. The aluminum oxide nanoparticles (Nanodur, Nanophase Inc. (Romeoville, IL, USA), density 3.97 g/cm³, diameter 50 nm, CAS number 1344-28-01) were used with or without an octyl(triethoxy)silane (C₈) coating. The C₈ surface modification was performed by dispersing nanoparticles in a mixture of water and 2-propanol. 25 wt.% ammonia (Sigma-Aldrich (St. Louis, MO, USA)) was added and the slurry was mechanically stirred for 5 min before n-octyl(triethoxy)silane (CAS-number 2943-75-1, 276.5 Da) was inserted. The suspension was allowed to react for 24 at 20 °C before the coated particles were washed and dried overnight [7]. All nanoparticles were soaked in 5 mL heptane, ultrasonicated (10 min) and mixed with LDPE powder. The resulting slurry was shaken for 60 min in a Vortex Genie 2 shaker (G560E, Scientific Industries (Bohemia, NY, USA)) and then dried overnight at 80 °C before extrusion and compression molding.

2.2. Material Characterization

Scanning electron microscopy (SEM) was used to study the nanoparticle dispersion and the crystal morphology of the materials. 0.3 mm thick circular pieces of each plaque sample were freeze-cracked in liquid nitrogen and acid-etched in a 10 mg KMnO₄/1 mL acid (H₂SO₄:H₃PO₄:H₂O (10:4:1)) solution for 1 h [34]. The permanganic acid-etched samples were sputtered with platinum (Cressington 208 HR) (20 s, 80 mA) and the cross-sectional morphology was examined with a Hitachi S-4800 field emission SEM. The fracture surfaces were analysed to ensure that the bulk material, rather than the surface, was investigated. The microstructure of LDPE/Al₂O₃ nanocomposites has also been carefully examined with SEM and transmission electron microscope TEM in our previous studies [7,35,36].

A differential scanning calorimeter (DSC 1) from Mettler Toledo was used for the calorimetric measurements and for determining endotherms. For each material, 5 ± 0.05 mg was placed in a covered aluminum pan, which was put into the DSC. A 50 mL min⁻¹ nitrogen environment was used. The temperature was ramped three times at a rate of 10 °C min⁻¹—first from −50 to 200 °C, then to −50 °C and, finally, to 200 °C. Between the temperature ramps, the temperature was kept constant for 5 min. The crystallinity and the melting peak temperature were evaluated from the first heating scan, to include the thermal history of the samples. Using the melting enthalpy (Δh_f) and the melting onset temperature (T₁) from the DSC measurements, the mass crystallinity (W_c) was assessed by the total enthalpy method [37]:

$$W_c=\frac{\mathsf{\Delta }{h}_f}{\mathsf{\Delta }{h}_f^0-{\displaystyle \underset{T_1}{\overset{T_m^0}{\int }}(c_{p,a}-c_{p,c})dT}}\times 100$$

(1)

where $T_m^0$ = 414.6 K [37] is the equilibrium melting point of PE, $\mathsf{\Delta }{h}_f^0$ = 293 J g⁻¹ [37] is the melting enthalpy for 100% crystalline PE and c_p,a, and c_p,c are the heat capacities for amorphous and crystalline LDPE, respectively [38,39]. The crystal thickness L_c (nm) was assessed by applying the Thomson–Gibbs equation to the melting temperature data, using a crystal density of ρ_c = 1000 kg/m³ and a fold surface energy of σ₀ = 90 mJ/m² [37]:

$$L_c=\left(\frac{2{\sigma }_0}{\mathsf{\Delta }{h}^0{\rho }_c}\right)\left(\frac{T_m^0}{T_m^0-T_m}\right)=0.614\left(\frac{T_m^0}{T_m^0-T_m}\right)$$

(2)

The Archimedes principle (with water) was used to measure the sample density ρ. The densities for Al₂O₃ and LDPE were ρ₁ = 3900 kg/m³ [40] and ρ₂ = 927 kg/m³ (measured), respectively. At particle weight fraction ϕ, the porosity was calculated as the ratio between ρ and the predicted density ρ₀ = (ρ₁ρ₂/(ϕρ₂ + (1 − ϕ)ρ₁).

2.3. Solubility (Sorption-Desorption)

The solubility was defined as the equilibrium mass fraction (wt.%) of the solutes (acetophenone or limonene) in the materials. The solubility was calculated from the absolute difference between the initial mass and the final (steady state) mass, either from a sorption or a desorption experiment. Sorption measurements were done by immersing 0.3 mm thick and 2.5 cm wide quadratic samples in tubes filled with acetophenone or limonene. The samples were removed at predefined time intervals. They were dried with clean serviettes, to get rid of excess solute on the surfaces, and then rapidly weighed before they were returned to the tubes. The weighing process continued until constant mass was reached. The desorption measurements were done by removing the saturated samples from the liquid and drying them in air. The weight was recorded over time until equilibrium was reached. The solubility of the limonene was measured at room temperature (21 °C), while acetophenone solubility was measured at both 21 and 60 °C. A single solubility measurement was done for each material/solute combination. The standard deviation estimates were assessed using a five-fold replicate of each solute.

2.4. Diffusivity (Sorption/Desorption)

For each material, the diffusivity (D) of acetophenone and limonene was calculated. The first strategy was to measure and utilize the time t_0.5, which is the time to reach 50% of the equilibrium concentration for a flat sample with thickness l [41]:

$$D=0.04919/(t_{0.5}/l^2)$$

(3)

This is an approximate method, considering that D is actually concentration dependent. A more elaborate strategy was to use a concentration dependent diffusivity D(c) and fit the experimental sorption/desorption data with Fick’s second law of diffusion [40]:

$$\frac{\partial c}{\partial t}=\frac{\partial c}{\partial x}\left(D(c)\frac{\partial c}{\partial x}\right)$$

(4)

Equation (4) was discretized and solved using an implicit finite difference multistep method [42,43]. The diffusivity D(c) was described by an exponential function, where D_c0 is the zero-concentration diffusivity and α is the plasticisation power [43]:

$$D(c)=D_{c0}\exp (\alpha c)$$

(5)

This is a semi-empirical equation which has been shown to properly describe the solute diffusivity of a number of systems [42,43,44]. During sorption, the concentration at the outer boundary was constant (c = c^eq), while during desorption, the boundary concentration was set to zero.

3. Results and Discussion

3.1. Material Characterization (SEM, Porosity and DSC)

Figure 2 reveals the composite structure of pristine LDPE and the LDPE-based nanocomposites with 3 wt.% Al₂O₃, 12 wt.% Al₂O₃ and 12 wt.% C₈-Al₂O₃. The uncoated Al₂O₃ nanoparticles agglomerated at high filler fractions, whereas the coated C₈-Al₂O₃ nanoparticles showed good dispersion, even at 12 wt.%. The addition of nanoparticles did not change the morphology of the LDPE component notably. A more detailed analysis of these LDPE/Al₂O₃ microstructures was presented in our previous studies [7,35,36].

The porosity, calculated from the measured nanocomposite densities (928–998 kg/m³), increased slightly with particle filler fraction for all materials, but the overall porosity was very low. Although the uncoated nanoparticles gave slightly higher porosities than the octyl-coated ones, the maximum porosity among all samples was still less than 0.7%.

The DSC measurements indicated no significant difference between extruded LDPE and extruded LDPE nanocomposites containing 3–12 wt.% Al₂O₃ or C₈-Al₂O₃ (

Table 1. Thermal characterization of the LDPE-based materials.

Sample	Property
	Tm a (°C)	Tc b (°C)	Lc c (nm)	Wc d (%)
PE (powder) b	112.8	98.9	8.9	46
PE-Hept (extruded)	111.1	99.1	8.6	50
PE-3wt.%-Al2O3-PNC	112.3	99.1	8.7	50
PE-6wt.%-Al2O3-PNC	111.6	99.1	8.5	48
PE-9wt.%-Al2O3-PNC	111.5	99.1	8.5	47
PE-12wt.%-Al2O3-PNC	113.0	98.9	8.9	49
PE-3wt.%-C8-Al2O3-PNC	111.8	99.3	8.5	52
PE-6wt.%-C8-Al2O3-PNC	111.7	99.3	8.5	53
PE-9wt.%-C8-Al2O3-PNC	110.9	99.5	8.3	50
PE-12wt.%-C8-Al2O3-PNC	112.8	99.1	8.9	49

^aT_m = peak melting temperature from the first melting curve with heating rate of 10 °C/min; ^b T_c = crystallization temperature with cooling rate of 10 °C/min; ^c L_c = lamellar thickness calculated using T_m; ^d W_c = weight percent crystallinity calculated from the first heating curve.

). The peak melting temperature (T_m) was 112 ± 1 °C, the melting onset temperature (T₁) was 99.2 ± 0.3 °C and the lamellar thickness (L_c) associated with the peak melting temperature, calculated using the Gibbs–Thomson equation [37], was 8.6 ± 0.3 nm for all materials. The crystallinity of extruded LDPE was 50% and there was no systematic trend in the nanocomposite crystallinity (50 ± 3%). Overall, the addition of nanoparticles had a limited impact on the crystalline nanostructure, as qualitatively confirmed with SEM (Figure 1). However, the non-extruded LDPE had a slightly lower crystallinity (45.5%) than that of the extruded materials (50%).

3.2. Solubility

The solubility of (polar) acetophenone in LDPE-based nanocomposites was plotted as a function of nanoparticle content in Figure 3a, using desorption data taken at 21 °C (

Table 2. Solubility and diffusivity. Acetophenone desorption data at 21 °C.

Sample	Solubility (wt.%)	D (Equation (3)) (×10−9 cm2 s−1)	Dc0 (Equation (5)) (×10−9 cm2s−1)
PE (extruded)	2.1	5.1	4.3
PE-3wt.%-Al2O3-PNC	2.1	5.6	4.4
PE-6wt.%-Al2O3-PNC	2.3	6.1	3.8
PE-9wt.%-Al2O3-PNC	2.4	5.9	3.9
PE-12wt.%-Al2O3-PNC	2.5	5.8	3.4
PE-3wt.%-C8-Al2O3-PNC	2.1	6.3	4.5
PE-6wt.%-C8-Al2O3-PNC	2.2	5.8	4.2
PE-9wt.%-C8-Al2O3-PNC	2.3	5.7	4.1
PE-12wt.%-C8-Al2O3-PNC	2.4	6.1	3.9

). The solubility increased linearly, with increasing filler fraction for both PE-Al₂O₃ and PE-C₈-Al₂O₃ nanocomposites. The slope increase was lower for the latter, because the C₈-coating made the particles more hydrophobic, which reduced their ability to adsorb the polar acetophenone. The linear functions are due to (1) the fact that an isolated nanoparticle can adsorb a fixed amount of acetophenone onto its surface and (2), at low filler content, the particles are well separated and do not interfere with each other [8]. The nanoparticles had a lower impact on the acetophenone solubility than on the water solubility [8,45]. However, the results still show that metal oxide nanoparticles such as Al₂O₃ can adsorb polar molecules, also larger than water, and thereby clean the surrounding polymer matrix from conductivity influencing impurities. At 60 °C, the acetophenone solubility was higher than at RT (5 wt.% versus ~2 wt.%), probably due to the higher accessible free volume after temperature-induced polymer swelling [46].

The (non-polar) limonene equilibrium mass uptake, measured during desorption at 21 °C, decreased linearly with nanoparticle filler fraction for both Al₂O₃ and C₈-Al₂O₃ nanoparticles (Figure 3b,

Table 3. Solubility and diffusivity. Limonene desorption data at 21 °C.

Sample	Solubility (wt.%)	D (Equation (3)) (×10−9 cm2 s−1)
PE (extruded)	12.9	29
PE-1wt.%-Al2O3-PNC	12.6	25
PE-3wt.%-Al2O3-PNC	12.7	32
PE-5wt.%-Al2O3-PNC	12.3	26
PE-10wt.%-Al2O3-PNC	12.0	32
PE-1wt.%-C8-Al2O3-PNC	13.1	26
PE-3wt.%-C8-Al2O3-PNC	12.7	31
PE-5wt.%-C8-Al2O3-PNC	12.7	29
PE-10wt.%-C8-Al2O3-PNC	12.5	26

). This is in direct contrast with the trend for acetophenone, where the solubility increased linearly with the filler fraction. The limonene uptake in LDPE was clearly higher (~13 wt.%) than the corresponding acetophenone uptake (~2 wt.%), due to the non-polar character of both LDPE and limonene.

3.3. Diffusion

During (polar) acetophenone sorption and desorption in extruded LDPE, only a minor (diffusion) concentration dependence was observed at 21 and 60 °C (Figure 4). Therefore, the diffusion pre-exponent D_c0 (Equation (5)), was just a little lower than the concentration independent diffusivity D (Equation (3)) (Table 1). The presence of 1–12 wt.% (0–4 vol.%) spherical Al₂O₃ nanoparticles (with or without C₈-coating) had a negligible impact on the acetophenone diffusion. At 21 °C, mass equilibrium was reached within 11 h (sorption) or 25 h (desorption), and the desorption diffusivity was D (Equation (3) = (5.1–6.3) × 10⁻⁹ cm² s⁻¹. At 60 °C, the kinetic energy was higher and the free volume was larger than at 21 °C. Therefore, equilibrium was reached faster (1.4 for sorption and 2.7 h for desorption), and the diffusivity D (Equation (3)) = (95–100) × 10⁻⁹ cm² s⁻¹ was 20 times higher than at 21 °C. Non-extruded LDPE (at 21 and 60 °C) had a diffusivity that was twice as large as extruded LDPE, due to its lower crystallinity (45.5 vs. 50%) [47].

For (non-polar) limonene in extruded LDPE at 21°C, slightly S-shaped sorption curves were observed (Figure 4). S-shaped curves are typically caused by the time-dependent and non-symmetric swelling of the polymer matrix [40,45]. The addition of nanoparticles (Al₂O₃ or C₈-Al₂O₃) did not change the limonene diffusivity D (Equation (3)) = (25–32) × 10⁻⁹ cm² s⁻¹ (Table 2). Consequently, neither the equilibrium times for sorption (~1.5 h) or desorption (~10.4 h) were affected by the nanoparticles. The diffusivity for limonene was approximately 1 order of magnitude higher than for acetophenone, even although the limonene molecules were slightly larger. The higher limonene diffusivity was partly due to the non-polar nature of the limonene molecules, which reduces the adhesive interactions between the diffusing molecules and the polymer matrix, and partly due to the larger limonene solubility, which gives a more plasticized and swollen material with a larger free volume, thus facilitating penetrant diffusion.

It must be noted that the materials in this study were not crosslinked. Somewhat lower diffusivities are expected for the corresponding crosslinked LDPE nanocomposites, because crosslinking makes the polymer more rigid and decreases the accessible free volume and the mobility of the penetrant molecules.

3.4. Influence of Particle Size on the Solubility

Ceramics, such as Al₂O₃, are impermeable to many penetrant molecules. The solubility of acetophenone, limonene and water is, therefore, effectively zero in Al₂O₃. In contrast, the solubility (S_m) in the polymer matrix is larger than zero. Consequently, with sufficiently large Al₂O₃ particles, the composite solubility S decreases proportionally with the particle volume fraction ϕ_f, i.e., S = S_m × (1 − ϕ_f). However, in several nanocomposite studies, the composite solubility increased with increasing nanoparticle content [8,45]. The reason for this discrepancy is that surface effects dominate at the nanoscale. All particle surfaces can attract (or repel) sorbent molecules, but nanoparticles have a much higher specific surface area than macroscopic particles. Therefore, the overall composite solubility depends on both the particle filler content and the specific particle surface area, A₀/V₀ (m²/m³). For spherical particles with radius r, volume V₀ = 4πr³/3 (nm³) and surface area A₀ = 4πr² (nm²), it becomes A₀/V₀ = 3/r (nm⁻¹). The Al₂O₃ particles in this study had an average r = 25 nm [7]. At low-volume fractions of sufficiently small, well-dispersed polar nanoparticles, S is expected to increase linearly with both ϕ_f and A₀/V₀. The solubility expressions for large and small particles can then be combined into one single predictive Equation (7):

$$S({\varphi }_f)=(1-{\varphi }_f)S_m+{\varphi }_f{k}_0{A}_0/V_0=(1-{\varphi }_f)S_m+{\varphi }_f{k}_{0}3/r$$

(6)

with matrix solubility S_m (wt.%) and adsorption strength constant k₀ (wt.% nm). With polar nanoparticles, k₀ is expected to be positive (=attractive) for polar molecules and zero or even negative (=repulsive) for non-polar molecules. For very large particles, S will always decrease with ϕ_f, but, for smaller particles, S can either increase or decrease. The equation was in good agreement with the experimental solubility data of this study. For acetophenone, the constants were S₀ = 2.07 wt.%, k₀ = 95 nm wt.% (C₈-Al₂O₃) and k₀ = 121 (Al₂O₃). For limonene, they were S₀ = 12.85 wt.%, k₀ = 0 (C₈-Al₂O₃) and k₀ = 150 (Al₂O₃). In Figure 5, the experimental acetophenone solubilities for C₈-Al₂O₃ nanocomposites are plotted together with Equation (6), showing the predicted effect of the different particle sizes. A four-fold increase in particle radius from 25 to 100 nm changes the solubility slope from positive to negative, while a 16-fold increase (from 25 to 400 nm) results in composites with negligible surface effects.

It should be noted that k₀ will only be constant at relatively low ϕ_f values. A maximum ϕ_f of ~3 vol.% was used in this study. At higher filler fractions, when the particles start to influence each other, k₀ is expected to gradually decrease.

A Monte Carlo model was used to assess the composite solubility at higher filler fractions of well-dispersed spherical particles. The composite was assumed to consist of three regions with distinctly different solubilities: the filler (with solubility S_f = 0), the matrix (with solubility S_m) and the interphase between the filler and the matrix (with solubility S_I). Spherical particles with radius r, surrounded by an interphase with thickness d, were randomly placed in cubical simulation domains with size (20 r)³. The average volume fractions of filler (ϕ_f), matrix (ϕ_m) and interphase (ϕ_I) were calculated for 100 simulation domains. The curves for ϕ_I versus ϕ_f were accurately fitted with third order polynomials (Figure 6a). In turn, the polynomial coefficients were fitted with two to four order polynomials as a function of δ = d/r (Figure 6b). The thin interlayer thicknesses (d) resulted in nearly linear ϕ_I versus ϕ_f curves, whereas thicker interlayers resulted in curves with increasingly pronounced curvature. For systems with very thick interlayers, corresponding to very small particles, the interlayer volume fraction was no longer monotonically increasing in the range 0–25 vol.% particles. Generally, the scattering of the data was exceedingly small, because of the large size of the simulation domain and the large number of replicates, and the deviation between the simulation data points and the fitted curves was negligible. Using the data from Figure 6, the composite solubility S becomes:

$$\begin{array}{l}S({\varphi }_f)=S_f{\varphi }_f+S_I{\varphi }_I+S_m(1-{\varphi }_f-{\varphi }_I)\\ {\varphi }_I=p_1{\varphi }_f^3+p_2{\varphi }_f^2+p_3{\varphi }_f\\ p_1=89.1{\delta }^4-67.8{\delta }^3-13.5{\delta }^2+4.09\delta \\ p_2=-43.9{\delta }^3+29.1{\delta }^2-4.82\delta \\ p_3=4.7{\delta }^2+2.36\delta \end{array}$$

(7)

Equation (7) is valid in a larger filler fraction range than Equation (6), but has the drawback that two solubility measurements with different r must be made in order to determine both the interphase solubility and the relative interphase thickness δ = d/r. Equation (6) is only valid for small filler fractions (unless r is large or the solute is nonpolar), but it is intuitive and easy to use, valid for non-spherical fillers, and the parameters can be determined using a single particle size.

4. Conclusions

The electrical conductivity of polyethylene (PE) is significantly reduced when small fractions of metal oxide nanoparticles are dispersed in it. A hypothesis is that (conductivity increasing) ions and polar molecules adsorb onto the nanoparticle surfaces, leading to the cleaning of the bulk of the polymer, and thereby decreasing the conductivity of the nanocomposite when compared to the pure PE. The solubility of (polar) acetophenone increased linearly with increasing nanoparticle content in PE-Al₂O₃ and PE-C₈-Al₂O₃ nanocomposites, whereas the solubility of (non-polar) limonene showed a decrease with increasing nanoparticle content. The diffusivities of both acetophenone and limonene were essentially independent of the nanoparticle fraction in the composites. These findings strengthen the surface attraction hypothesis and provide fundamental information for the optimization of the electrical properties of insulation nanocomposites, especially for HVDC applications. Additionally, two novel equations for predicting composite solubility as a function of filler fraction, particle size and adsorption strength were derived. The first semi-empirical equation (Equation 6) can elegantly describe how particle size and particle filler fraction influence the composite solubility, only requiring the matrix solubility and the particle adsorption strength as input—i.e., only two solubility measurements at different filler fractions are required to determine the two constants. The second equation (Equation (7)), which is based on accurate data from the Monte Carlo simulations, describes the sorption in nano-composites with high particle filler fractions more correctly, but it has one additional unknown parameter that has to be determined with experimental measurements when compared to Equation (6).