Dual Closed-Loop Linear Active Disturbance Rejection Control of Grid-Side Converter of Permanent Magnet Direct-Drive Wind Turbine
Abstract
:1. Introduction
2. Control Strategy of Traditional Grid-side Converter
2.1. Mathematical Model of Wind Power Grid-connected Converter
2.2. Control Strategy of Dual closed-loop Grid-Side Converter Based on PI Control
3. Design and Frequency Domain Analysis of LADRC
3.1. Design of First-order LADRC
3.2. Frequency Domain Analysis of the First-order LADRC
3.2.1. Convergence and Estimation Error Analysis of Second-order LESO
3.2.2. Analysis of the Anti-disturbance Characteristics of LADRC
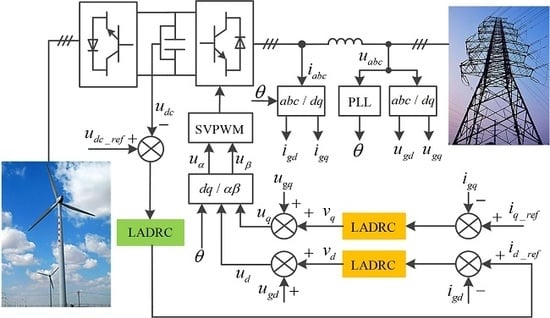
4. Control Strategy of Grid-side Converter Based on LADRC
4.1. Design of Current Inner Loop Control System Based on First-order LADRC
4.2. Design of Voltage Outer Loop Control System Based on First-order LADRC
5. Simulation Analysis
5.1. Simulation Comparison of Current Inner Loop Decoupling Control
5.2. Simulation Comparison of Voltage Stabilizing Control of Voltage Outer Loop
5.3. Comparison between Traditional PI Dual closed-loop Control and LADRC Based Dual closed-loop Control
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronym | Definition |
| NADRC | Nonlinear active disturbance rejection control |
| LADRC | Line active disturbance rejection control |
| LESO | Linear extended state observer |
| LTD | Linear tracking differentiator |
| LSEF | Linear state error feedback |
| PI | Proportional integral |
| DC | Direct current |
| AC | Alternating current |
Appendix A
| Parameter | Value | Unit |
|---|---|---|
| Base power | 1.5 | MW |
| Base voltage | 690 | V |
| Base frequency | 50 | Hz |
| DC link voltage | 1070 | V |
| DC capacitance | 0.024 | F |
| Grid-side filter resistance | 0.0009 | |
| Grid-side filter inductance | 0.12 | mH |
| Grid-side filter capacitance | 0.0015 | F |
| Parameter | Value |
|---|---|
| Inner loop PI controller parameters | 0.8 |
| Inner loop PI controller parameters | 10 |
| Outer loop PI controller parameters | 9.8 |
| Outer loop PI controller parameters | 98 |
| Inner loop observer bandwidth | 700 |
| Inner loop observer bandwidth | 5000 |
| Outer Loop Observer Bandwidth | 70 |
| Outer Loop Observer Bandwidth | 300 |
References
- Tafti, H.D.; Maswood, A.I.; Konstantinou, G.; Townsend, C.D.; Acuna, P.; Pou, J. Flexible control of photovoltaic grid-connected cascaded H-bridge converters during unbalanced voltage sags. IEEE Trans. Ind. Electron. 2018, 65, 6229–6238. [Google Scholar] [CrossRef]
- Huenteler, J.; Niebuhr, C.; Schmidt, T.S. The effect of local and global learning on the cost of renewable energy in developing countries. J. Clean. Prod. 2016, 128, 6–21. [Google Scholar] [CrossRef]
- Manoj, S.P.; Vijayakumari, A.; Sasi, K.K. Development of a Comprehensive MPPT for grid-connected wind turbine driven PMSG. Wind Energy 2019, 22, 732–744. [Google Scholar]
- Yan, J.H.; Lin, H.Y.; Feng, Y.; Zhu, Z.Q. Control of a grid-connected direct-drive wind energy conversion system. Renew. Energy 2014, 66, 371–380. [Google Scholar] [CrossRef]
- Chinmaya, K.A.; Singh, G.K. Modeling and experimental analysis of grid-connected six-phase induction generator for variable speed wind energy conversion system. Electr. Power Syst. Res. 2019, 166, 151–162. [Google Scholar] [CrossRef]
- Lee, S.W.; Chun, K.H. Adaptive Sliding Mode Control for PMSG Wind Turbine Systems. Energies 2019, 12, 595. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.R.; Gao, C.; Wang, Z.L. A Nonlinear Disturbance Observer Based DC-bus Voltage Control for PV Grid-connected Inverter. Power Syst. Tech. 2019, 5, 1–11. [Google Scholar]
- Jia, J.C. Optimal Combination Control of Dual Converters in Doubly-Fed Wind Power Generation System. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2011. [Google Scholar]
- Xiao, L. Control on Direct-drive Wind Turbine with PM Synchronous Generator under Unbalanced Grid Voltage Conditions. Ph.D. Thesis, Hunan University, Changsha, China, 2013. [Google Scholar]
- Li, K. Research on Grid-connected Control for Converter of Direct-drive Wind Power Generator. Bachelor’s Thesis, Xihua University, Chengdu, China, 2014. [Google Scholar]
- Long, B.; Wang, W.; Huang, L.J.; Chen, Y.; Li, F.S.; Sun, H.B.; Li, H. Design and implementation of a virtual capacitor based DC current suppression method for grid-connected inverters. ISA Trans. 2019, 92, 257–272. [Google Scholar] [CrossRef]
- Xu, X.Y. Research on Control Strategy of Grid Side Inverter for Wind Power. Bachelor’s Thesis, North China Electric Power University, Beijing, China, 2017. [Google Scholar]
- Sun, Z.N.; Wang, D.Z.; Yuan, T.Q.; Liu, Z.R.; Yu, J.H. A Novel Control Strategy for Grid-Connected Inverter Based on Iterative Calculation of Structural Parameters. Energies 2018, 11, 16. [Google Scholar] [CrossRef] [Green Version]
- Han, J.Q. Active Disturbance Rejection Control Technique—The Technique for Estimating and Compensating the Uncertainties; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Han, J.Q. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, Y.; Ai, W.; Zhou, Z. Precision motion control of permanent magnet linear motors. Int. J. Adv. Manuf. Technol. 2007, 35, 301–308. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, L.; Chen, J.; Tang, X.; Song, Y.; He, Y. Current double closed loop control of LCL grid connected inverter. Power Syst. Prot. Control 2016, 44, 52–57. [Google Scholar]
- He, N.; Xu, D.; Zhu, Y.; Zhang, J.; Shen, G.; Zhang, Y.; Ma, J.; Liu, C. Weighted Average Current Control in a Three-Phase Grid Inverter with an LCL Filter. IEEE Trans. Power Electron. 2013, 28, 2785–2797. [Google Scholar] [CrossRef]
- Qu, K.; Li, W.; Ye, T. Decoupling control strategy of LCL inverter based on state feedback. Trans. China Electrotech. Soc. 2016, 31, 130–138. [Google Scholar]
- Li, C.P.; Ben, H.Q.; Liu, B.; Sun, S.H. Deviation decoupling control method based on disturbance observer. Proc. CSEE 2015, 35, 5859–5868. [Google Scholar]
- Ali, M.; Yaqoob, M.; Cao, L.L.; Loo, K.H. Disturbance-Observer-Based DC-Bus Voltage Control for Ripple Mitigation and Improved Dynamic Response in Two-Stage Single-Phase Inverter System. IEEE Trans. Ind. Electron. 2019, 66, 6836–6845. [Google Scholar] [CrossRef]
- Vijayakumari, A.; Devarajan, A.T.; Devarajan, N.; Vijith, K. Dynamic grid impedance calculation in D–Q frame for micro-grids. In Proceedings of the 2014 Power and Energy Systems: Towards Sustainable Energy, Bangalore, India, 13–15 March 2014; pp. 1–6. [Google Scholar]
- Zhou, X.S.; Liu, M.; Ma, Y.J.; Yang, B.; Zhao, F.Q. Linear Active Disturbance Rejection Control for DC Bus Voltage of Permanent Magnet Synchronous Generator Based on Total Disturbance Differential. Energies 2019, 12, 22. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.Q. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the IEEE 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Shan, Z.; Jatskevich, J. A feedforward control method of dual-active-bridge DC/DC converter to achieve fast dynamic response. In Proceedings of the 2014 IEEE 36th International Telecommunications Energy Conference (INTELEC), Vancouver, BC, Canada, 28 September–2 October 2014; pp. 1–6. [Google Scholar]
- Zhang, Z.; Wang, F.; Wang, J.; Rodríguez, J.; Kennel, R. Nonlinear Direct Control for Three-Level NPC Back-to-Back Converter PMSG Wind Turbine Systems: Experimental Assessment with FPGA. IEEE Trans. Ind. Inform. 2017, 13, 1172–1183. [Google Scholar] [CrossRef]
- Gao, Y.G.; Jiang, F.Y.; Song, J.C.; Zheng, L.J.; Tian, F.Y.; Geng, P.L. A novel dual closed-loop control scheme based on repetitive control for grid-connected inverters with an LCL filter. ISA Trans. 2018, 74, 194–208. [Google Scholar] [CrossRef]
- Errouissi, R.; Al-Durra, A.; Debouza, M. A Novel Design of PI Current Controller for PMSG-Based Wind Turbine Considering Transient Performance Specifications and Control Saturation. IEEE Trans. Ind. Electron. 2018, 65, 8624–8634. [Google Scholar] [CrossRef]
- Zhou, X.; Tian, C.; Ma, Y. SHAPF model based on LADRC and its current tracking control. Electr. Power Autom. Equip. 2013, 33, 49–54. [Google Scholar]
- Huang, Y.; Xue, W. Active disturbance rejection control: Methodology and theoretical analysis. ISA Trans. 2014, 53, 963–976. [Google Scholar] [CrossRef] [PubMed]
- Yuan, D.; Ma, X.J.; Zeng, Q.H.; Qiu, X. Research on frequency-band characteristics and parameters configuration of linear active disturbance rejection control for second-order systems. Control Theory Appl. 2013, 30, 1630–1640. [Google Scholar]

















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Yang, X.; Zhou, X.; Yang, L.; Zhou, Y. Dual Closed-Loop Linear Active Disturbance Rejection Control of Grid-Side Converter of Permanent Magnet Direct-Drive Wind Turbine. Energies 2020, 13, 1090. https://doi.org/10.3390/en13051090
Ma Y, Yang X, Zhou X, Yang L, Zhou Y. Dual Closed-Loop Linear Active Disturbance Rejection Control of Grid-Side Converter of Permanent Magnet Direct-Drive Wind Turbine. Energies. 2020; 13(5):1090. https://doi.org/10.3390/en13051090
Chicago/Turabian StyleMa, Youjie, Xia Yang, Xuesong Zhou, Luyong Yang, and Yongliang Zhou. 2020. "Dual Closed-Loop Linear Active Disturbance Rejection Control of Grid-Side Converter of Permanent Magnet Direct-Drive Wind Turbine" Energies 13, no. 5: 1090. https://doi.org/10.3390/en13051090
APA StyleMa, Y., Yang, X., Zhou, X., Yang, L., & Zhou, Y. (2020). Dual Closed-Loop Linear Active Disturbance Rejection Control of Grid-Side Converter of Permanent Magnet Direct-Drive Wind Turbine. Energies, 13(5), 1090. https://doi.org/10.3390/en13051090