Improved Hydrogen-Production-Based Power Management Control of a Wind Turbine Conversion System Coupled with Multistack Proton Exchange Membrane Electrolyzers †
Abstract
:1. Introduction
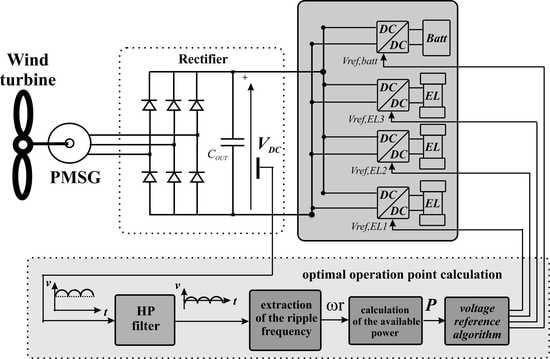
2. Wind Turbine Conversion System Coupled with Multistack PEM Electrolyzers
3. Characterization of the Wind Turbine
3.1. Turbine Modeling
3.2. Experimental Characterization
4. Characterization of the Electrolyzer
4.1. Static Characterization
4.2. Dynamic Characterization
5. Converter Modeling and Characterization
6. Power Management Strategy
6.1. Turbine Power Estimation
6.2. Power Sharing Strategy
7. Experimental Validation of the Power Management Strategy
7.1. Test Rig Description
7.2. Experimental Results
7.3. Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Panwar, N.L.; Kaushik, S.C.; Kothari, S. Role of renewable energy sources in environmental protection: A review. Renew. Sustain. Energy Rev. 2011, 15, 1513–1524. [Google Scholar] [CrossRef]
- Available online: https://www.cleantech.com/the-role-of-green-hydrogen-in-global-decarbonization/ (accessed on 26 September 2019).
- Available online: https://www.iea.org/tcep/energyintegration/hydrogen/ (accessed on 26 September 2019).
- Byfield, S.; Vetter, D. Flexibility Concepts for the German Power Supply in 2050: Ensuring Stability in the Age of Renewable Energies; Acatech–Deutsche Akademie der Technikwissenschaften: Munich, Germany, 2016. [Google Scholar]
- Lund, P.; Lindgren, J.; Mikkola, J.; Salpakari, J. Review of energy system flexibility measures to enable high levels of variable renewable electricity. Renew. Sustain. Energy Rev. 2015, 45, 785–807. [Google Scholar] [CrossRef] [Green Version]
- Mohanpurkar, M.; Luo, Y.; Terlip, D.; Dias, F.; Harrison, K.; Eichman, J.; Hovsapian, R.; Kurtz, J. Electrolyzers Enhancing Flexibility in Electric Grids. Energies 2017, 10, 1836. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.-C.; Lin, K.-M. Impacts of Load Profiles on the Optimization of Power Management of a Green Building Employing Fuel Cells. Energies 2019, 12, 57. [Google Scholar] [CrossRef] [Green Version]
- Valencia, G.; Benavides, A.; Cárdenas, Y. Economic and Environmental Multiobjective Optimization of a Wind–Solar–Fuel Cell Hybrid Energy System in the Colombian Caribbean Region. Energies 2019, 12, 2119. [Google Scholar] [CrossRef] [Green Version]
- Sarrias-Mena, R.; Fernández-Ramírez, L.M.; García-Vásquez, C.A.; Jurado, F. Electrolyzer models for hydrogen production from wind energy systems. Int. J. Hydrog. Energy 2015, 40, 2927–2938. [Google Scholar] [CrossRef]
- Zhou, T.; François, B.; El Hadi Lebbal, M.; Lecoeuche, S. Real-Time Emulation of a Hydrogen-Production Process for Assessment of an Active Wind-Energy Conversion System. IEEE Trans. Ind. Electron. 2009, 56, 737–746. [Google Scholar] [CrossRef]
- Gandia, L.M.; Arzamedi, G.; Diéguez, P.M. Renewable Hydrogen Technologies: Production, Purification, Storage, Applications and Safety; Newnes: London, UK, 2013. [Google Scholar]
- Koponen, J.; Ruuskanen, V.; Kosonen, A.; Niemelä, M.; Ahola, J. Effect of Converter Topology on the Specific Energy Consumption of Alkaline Water Electrolyzers. IEEE Trans. Power Electron. 2018, 34, 6171–6182. [Google Scholar] [CrossRef]
- Rodriguez, J.; Pontt, J.; Silva, C.; Wiechmann, E.; Hammond, P.; Santucci, F.; Alvarez, R.; Musalem, R.; Kouro, S.; Lezana, P. Large current rectifiers: State of the art and future trends. IEEE Trans. Ind. Electron. 2005, 52, 738–746. [Google Scholar] [CrossRef]
- Solanki, J.; Fröhleke, N.; Böcker, J.; Wallmeier, P. Comparison of Thyristor-Rectifier with Hybrid Filter and Chopper-Rectifier for High-Power High-Current Application. In Proceedings of the PCIM Europe 2013, Nuremberg, Germany, 14–16 May 2013; pp. 1391–1398. [Google Scholar]
- Solanki, J.; Fröhleke, N.; Böcker, J. Implementation of hybrid filter for 12-pulse thyristor rectifier supplying high-current variable-voltage DC load. IEEE Trans. Ind. Electron. 2015, 62, 4691–4701. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Takahashi, R.; Tamura, J. Electrolyzer switching strategy for hydrogen generation from variable speed wind generator. Electr. Power Syst. Res. 2011, 81, 1171–1179. [Google Scholar] [CrossRef] [Green Version]
- Pascuzzi, S.; Anifantis, A.; Blanco, I.; Scarascia, G. Electrolyzer performance analysis of an integrated hydrogen power system for greenhouse heating. A Case Study. Sustainability 2016, 8, 629. [Google Scholar] [CrossRef] [Green Version]
- Haruni, A.O.; Negnevitsky, M.; Haque, M.E.; Gargoom, A. A novel operation and control strategy for a standalone hybrid renewable power system. IEEE Trans. Sust. Energy 2013, 4, 402–413. [Google Scholar] [CrossRef]
- Trifkovic, M.; Sheikhzadeh, M.; Nigim, K.; Daoutidis, P. Modeling and control of a renewable hybrid energy system with hydrogen storage. IEEE Trans. Control Syst. Technol. 2014, 22, 169–179. [Google Scholar] [CrossRef]
- Takahashi, R.; Kinoshita, H.; Murata, T.; Tamura, J.; Sugimasa, M.; Komura, A.; Ide, K. Output power smoothing and hydrogen production by using variable speed wind generators. IEEE Trans. Ind. Electron. 2010, 57, 485–493. [Google Scholar] [CrossRef]
- Yamashita, D.; Nakao, H.; Yonezawa, Y.; Nakashima, Y.; Ota, Y.; Nishioka, K.; Sugiyama, M. A New Solar to Hydrogen Conversion System with High Efficiency and Flexibility. In Proceedings of the IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA) 2017, San Diego, CA, USA, 5–8 November 2017; pp. 441–446. [Google Scholar]
- Marx, N.; Boulon, L.; Gustin, F.; Hissel, D.; Agbossou, K. A review of multistack and modular fuel cell systems: Interests, application areas and on-going research activities. Int. J. Hydrog. Energy 2014, 39, 12101–12111. [Google Scholar] [CrossRef]
- Liso, V.; Savoia, G.; Araya, S.S.; Cinti, G.; Kær, S.K. Modelling and Experimental Analysis of a Polymer Electrolyte Membrane Water Electrolysis Cell at Different Operating Temperatures. Energies 2018, 11, 3273. [Google Scholar] [CrossRef] [Green Version]
- Onda, K..; Murakami, T.; Hikosaka, T.; Kobayashi, M.; Notu, R.; Ito, K. Performance Analysis of Polymer-Electrolyte Water Electrolysis Cell at a Small-Unit Test Cell and Performance Prediction of Large Stacked Cell. J. Electrochem. Soc. 2002, 149, A1069–A1078. [Google Scholar] [CrossRef]
- Guilbert, D.; Sorbera, D.; Vitale, G. A stacked interleaved DC–DC buck converter for proton exchange membrane electrolyzer applications: Design and experimental validation. Int. J. Hydrogen Energy 2020, 45, 64–79. [Google Scholar] [CrossRef]
- Dobo, Z.; Bence Palotas, Á.; Toth, P. The effect of power supply ripple on dc water electrolysis efficiency. Mater. Sci. Eng. 2016, 41, 23–31. [Google Scholar]
- Ursúa, A.; Sanchis, P.; Marroyo, L. Chapter 14—Electric conditioning and efficiency of hydrogen production systems and their integration with renewable energies. In Renewable Hydrogen Technologies; Gandía, L., Arzamendi, G., Diéguez, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 333–360. [Google Scholar]
- Ursúa, A.; Marroyo, L.; Gubía, E.; Gandía, L.M.; Diéguez, P.M.; Sanchis, P. Influence of the power supply on the energy efficiency of an alkaline water electrolyser. Int. J. Hydrog. Energy 2009, 34, 3221–3233. [Google Scholar] [CrossRef]
- Malkow, T.; Pilenga, A.; Tsotridis, G. EU Harmonised Test Procedure: Electrochemical Impedance Spectroscopy for Water Electrolysis Cells; EUR 29267 EN; Publications Office of the European Union: Brussels, Belgium, 2018. [Google Scholar] [CrossRef]
- Guilbert, D.; Vitale, G. Optimal Hydrogen Production from Direct Coupled Variable Speed Wind Generator with a Stacked Interleaved Buck Converter. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar]
- Guilbert, D.; Vitale, G. Dynamic Emulation of a PEM-ELectrolyzer by Time Constant Based Exponential Model. Energies 2019, 12, 750. [Google Scholar] [CrossRef] [Green Version]
- Ayivor, P.; Torres, J.; Meijden, M.V.; Stouwie, B. Modelling of Large Size Electrolyzer for Electrical Grid Stability Studies in Real Time Digital Simulation. In Proceedings of the 3rd International Hybrid Power Systems Workshop, Tenerife, Spain, 8–9 May 2018. [Google Scholar]
- Kolar, J.W.; Krismer, F.; Lobsiger, Y.; Muhlethaler, J.; Nussbaumer, T.; Minibock, J. Extreme Efficiency Power Electronics. In Proceedings of the IEEE 7th International Conference on Integrated Power Electronics Systems (CIPS), Nuremberg, Germany, 6–8 March 2012; pp. 1–22. [Google Scholar]

















| Specification | Data |
|---|---|
| Rated power (W) | 5000 |
| Max power (W) | 5800 |
| Wind speed (m/s) | |
| Cut in | 2.5 |
| Rated | 17 |
| Survival | 60 |
| Rotor blades | |
| Number | 3 |
| Diameter (m) | 5 |
| Swept area (m2) | 19.63 |
| Airfoil | E387 |
| Tip speed ratio | 7 |
| Material | Glass-fiber reinforced epoxy |
| Generator | |
| Type | Brushless permanent magnet 9-pole |
| Revolutions per minute operating range | 120–450 rpm |
| Frequency (Hz) | 0–70 |
| Gearbox | None |
| Specification | Data |
|---|---|
| Maximum H2 flow rate at standard temperature and pressure (STP).(20 °C/1 bar absolute) | 1 L/min |
| Delivery output pressure | 0.1–10.5 bar |
| H2 purity | >99.9999% |
| Electrolysis cell | Solid polymer membrane |
| Water | Deionized or distilled |
| Weight (dry) | 20 kg |
| Stack weight | 6 kg |
| Number of cells | 3 |
| Operating conditions: Temperature Relative humidity | 15 °C to 40 °C 0–80% |
| Stack operating voltage range | 4.4–8 V |
| Stack current range | 0–50 A |
| Stack rated electrical power | 400 W |
| Parameter | Value | Unit |
|---|---|---|
| Vint | 4.38 | (V) |
| Rint | 0.088 | (Ω) |
| R1 | 0.035 | (Ω) |
| R2 | 0.318 | (Ω) |
| C1 | 37.26 | (F) |
| C2 | 37.26 | (F) |
| Open Loop Poles of SIBC Loaded by a Static Model (104 rad/s) | Open Loop Poles of SIBC Loaded by a Dynamic Model (105 rad/s) |
|---|---|
| −0.0477 ± 1.6403i | −1.1320 + 0.0000i |
| −0.4803 ± 0.1252i | −0.0018 ± 0.1582i |
| - | −0.0037 + 0.0000i |
| - | −0.0000 + 0.0000i |
| Case | P | EL1 | EL2 | EL3 | Batt |
|---|---|---|---|---|---|
| 1 | P < 400 W | Vref,opt | OFF | OFF | OFF |
| 2 | 400 W < P < 800 W | Rated P | Vref,opt | OFF | OFF |
| 3 | 800 W < P < 1200 W | Rated P | Rated P | Vref,opt | OFF |
| 4 | P > 1200 W | Rated P | Rated P | Rated P | ON |
| Specification | Data |
|---|---|
| IGBT | 4xSKM 50 GB 123D |
| Rectifier | 1xSKD 51/14 |
| DC capacitor bank (at the output of the three-phase rectifier) | 2 × 2200 µF/400 V |
| Semikron driver boards | 4xSKHI 22 (0–15 V) |
| Passive components: | |
| Primary inductor, Lp | 400 µH |
| Secondary inductor, Ls | 400 µH |
| Parasitic resistances, Rp and Rs | 60 mΩ |
| Primary capacitor, Cp | 100 µF |
| Secondary capacitor, Cs | 10 µF |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guilbert, D.; Vitale, G. Improved Hydrogen-Production-Based Power Management Control of a Wind Turbine Conversion System Coupled with Multistack Proton Exchange Membrane Electrolyzers. Energies 2020, 13, 1239. https://doi.org/10.3390/en13051239
Guilbert D, Vitale G. Improved Hydrogen-Production-Based Power Management Control of a Wind Turbine Conversion System Coupled with Multistack Proton Exchange Membrane Electrolyzers. Energies. 2020; 13(5):1239. https://doi.org/10.3390/en13051239
Chicago/Turabian StyleGuilbert, Damien, and Gianpaolo Vitale. 2020. "Improved Hydrogen-Production-Based Power Management Control of a Wind Turbine Conversion System Coupled with Multistack Proton Exchange Membrane Electrolyzers" Energies 13, no. 5: 1239. https://doi.org/10.3390/en13051239
APA StyleGuilbert, D., & Vitale, G. (2020). Improved Hydrogen-Production-Based Power Management Control of a Wind Turbine Conversion System Coupled with Multistack Proton Exchange Membrane Electrolyzers. Energies, 13(5), 1239. https://doi.org/10.3390/en13051239