Defects and Dopants in CaFeSi2O6: Classical and DFT Simulations
Abstract
:1. Introduction
2. Computational Methods
3. Results
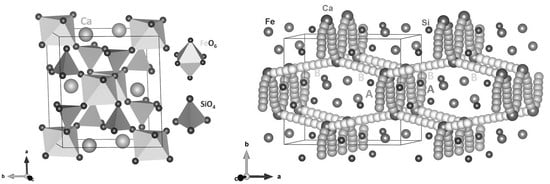
3.1. Crystal Structure of CaFeSi2O6
3.2. Intrinsic Defect Processes
3.3. Calcium Ion Diffusion
3.4. Solution of Dopants
3.4.1. Divalent Dopants
3.4.2. Trivalent Dopants
3.4.3. Tetravalent Dopants
3.5. Electronic Structures of Doped CaFeSi2O6
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Zhou, Y.; Zhang, J.; Xia, Y.; Chen, T.; Zhang, S. Monoclinic Phase Na3Fe2(PO4)3: Synthesis, Structure, and Electrochemical Performance as Cathode Material in Sodium-Ion Batteries. ACS Sustain. Chem. Eng. 2017, 5, 1306–1314. [Google Scholar] [CrossRef]
- Yabuuchi, N.; Kubota, K.; Dahbi, M.; Komaba, S. Research Development on Sodium-Ion Batteries. Chem. Rev. 2014, 114, 11636–11682. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.-Y.; Myung, S.-T.; Sun, Y.-K. Sodium-ion batteries: Present and future. Chem. Soc. Rev. 2017, 46, 3529–3614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.; Yoon, G.; Kim, H.; Park, Y.-U.; Kang, K. Na3V(PO4)2: A New Layered-Type Cathode Material with High Water Stability and Power Capability for Na-Ion Batteries. Chem. Mater. 2018, 30, 3683–3689. [Google Scholar] [CrossRef]
- Xu, C.; Li, B.; Du, H.; Kang, F. Energetic Zinc Ion Chemistry: The Rechargeable Zinc Ion Battery. Angew. Chem. Int. Ed. 2012, 51, 933–935. [Google Scholar] [CrossRef]
- Muldoon, J.; Bucur, C.B.; Gregory, T. Quest for Nonaqueous Multivalent Secondary Batteries: Magnesium and Beyond. Chem. Rev. 2014, 114, 11683–11720. [Google Scholar] [CrossRef] [PubMed]
- Ponrouch, A.; Frontera, C.; Bardé, F.; Palacín, M.R. Towards a calcium-based rechargeable battery. Nat. Mater. 2015, 15, 169–172. [Google Scholar] [CrossRef] [Green Version]
- Novák, P.; Imhof, R.; Haas, O. Magnesium insertion electrodes for rechargeable nonaqueous batteries—A competitive alternative to lithium? Electrochim. Acta 1999, 45, 351–367. [Google Scholar] [CrossRef]
- Aurbach, D.; Gofer, Y.; Lu, Z.; Schechter, A.; Chusid, O.; Gizbar, H.; Cohen, Y.; Ashkenazi, V.; Moshkovich, M.; Turgeman, R.; et al. A short review on the comparison between Li battery systems and rechargeable magnesium battery technology. J. Power Sources 2001, 97, 28–32. [Google Scholar] [CrossRef]
- Gummow, R.J.; Vamvounis, G.; Kannan, M.B.; He, Y. Calcium-Ion Batteries: Current State-of-the-Art and Future Perspectives. Adv. Mater. 2018, 30, 1801702. [Google Scholar] [CrossRef]
- Torres, A.; Luque, F.J.; Tortajada, J.; Arroyo-de Dompablo, M.E. Analysis of Minerals as Electrode Materials for Ca-based Rechargeable Batteries. Sci. Rep. 2019, 9, 9644. [Google Scholar] [CrossRef] [PubMed]
- Dompablo, M.E.A.-d.; Krich, C.; Nava-Avendaño, J.; Biškup, N.; Palacín, M.R.; Bardé, F. A Joint Computational and Experimental Evaluation of CaMn2O4 Polymorphs as Cathode Materials for Ca Ion Batteries. Chem. Mater. 2016, 28, 6886–6893. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Ahsbahs, H.; Hafner, S.S.; Kutoglu, A. Single-crystal compression and crystal structure of clinopyroxene up to 10 GPa. Am. Mineral. 1997, 82, 245–258. [Google Scholar] [CrossRef]
- Nishimura, S.-I.; Hayase, S.; Kanno, R.; Yashima, M.; Nakayama, N.; Yamada, A. Structure of Li2FeSiO4. J. Am. Chem. Soc. 2008, 130, 13212–13213. [Google Scholar] [CrossRef] [PubMed]
- Law, M.; Ramar, V.; Balaya, P. Na2MnSiO4 as an attractive high capacity cathode material for sodium-ion battery. J. Power Sources 2017, 359, 277–284. [Google Scholar] [CrossRef]
- Redfern, S.A.T.; Artioli, G.; Rinaldi, R.; Henderson, C.M.B.; Knight, K.S.; Wood, B.J. Octahedral cation ordering in olivine at high temperature. II: An in situ neutron powder diffraction study on synthetic MgFeSiO4 (Fa50). Phys. Chem. Miner. 2000, 27, 630–637. [Google Scholar] [CrossRef]
- Kuganathan, N.; Islam, M.S. Li2MnSiO4 Lithium Battery Material: Atomic-Scale Study of Defects, Lithium Mobility, and Trivalent Dopants. Chem. Mater. 2009, 21, 5196–5202. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defects, Dopants and Sodium Mobility in Na2MnSiO4. Sci. Rep. 2018, 8, 14669. [Google Scholar] [CrossRef]
- Armstrong, A.R.; Kuganathan, N.; Islam, M.S.; Bruce, P.G. Structure and Lithium Transport Pathways in Li2FeSiO4 Cathodes for Lithium Batteries. J. Am. Chem. Soc. 2011, 133, 13031–13035. [Google Scholar] [CrossRef] [Green Version]
- Liivat, A.; Thomas, J.O. Li-ion migration in Li2FeSiO4-related cathode materials: A DFT study. Solid State Ion. 2011, 192, 58–64. [Google Scholar] [CrossRef]
- Rupasov, D.; Chroneos, A.; Parfitt, D.; Kilner, J.A.; Grimes, R.W.; Istomin, S.Y.; Antipov, E.V. Oxygen diffusion in Sr0.75Y0.25CoO2.625: A molecular dynamics study. Phys. Rev. B 2009, 79, 172102. [Google Scholar] [CrossRef] [Green Version]
- Grimes, R.W.; Busker, G.; McCoy, M.A.; Chroneos, A.; Kilner, J.A.; Chen, S.-P. The Effect of Ion Size on Solution Mechanism and Defect Cluster Geometry. Ber. Der Bunsenges. Für Phys. Chem. 1997, 101, 1204–1210. [Google Scholar] [CrossRef]
- Jay, E.E.; Rushton, M.J.D.; Chroneos, A.; Grimes, R.W.; Kilner, J.A. Genetics of superionic conductivity in lithium lanthanum titanates. Phys. Chem. Chem. Phys. 2015, 17, 178–183. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Kordatos, A.; Chroneos, A. Li2SnO3 as a Cathode Material for Lithium-ion Batteries: Defects, Lithium Ion Diffusion and Dopants. Sci. Rep. 2018, 8, 12621. [Google Scholar] [CrossRef] [Green Version]
- Kuganathan, N.; Chroneos, A. Defects and dopant properties of Li3V2(PO4)3. Sci. Rep. 2019, 9, 333. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defect Chemistry and Na-Ion Diffusion in Na3Fe2(PO4)3 Cathode Material. Materials 2019, 12, 1348. [Google Scholar] [CrossRef] [Green Version]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Kuganathan, N.; Ganeshalingam, S.; Chroneos, A. Defects, Diffusion, and Dopants in Li2Ti6O13: Atomistic Simulation Study. Materials 2019, 12, 2851. [Google Scholar] [CrossRef] [Green Version]
- Catlow, C.R.A. “SolidState Chemistry: Techniques”; Cheetham, A.K., Day, P., Eds.; Clarendon Press: Oxford, UK, 1987; p. 231. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992; p. 994. [Google Scholar]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: New York, NY, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Ensling, D.; Stjerndahl, M.; Nytén, A.; Gustafsson, T.; Thomas, J.O. A comparative XPS surface study of Li2FeSiO4/C cycled with LiTFSI- and LiPF6-based electrolytes. J. Mater. Chem. 2009, 19, 82–88. [Google Scholar] [CrossRef]
- Liu, H.; Choe, M.-J.; Enrique, R.A.; Orvañanos, B.; Zhou, L.; Liu, T.; Thornton, K.; Grey, C.P. Effects of Antisite Defects on Li Diffusion in LiFePO4 Revealed by Li Isotope Exchange. J. Phys. Chem. C 2017, 121, 12025–12036. [Google Scholar] [CrossRef]
- Kempaiah Devaraju, M.; Duc Truong, Q.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef] [Green Version]
- Politaev, V.V.; Petrenko, A.A.; Nalbandyan, V.B.; Medvedev, B.S.; Shvetsova, E.S. Crystal structure, phase relations and electrochemical properties of monoclinic Li2MnSiO4. J. Solid State Chem. 2007, 180, 1045–1050. [Google Scholar] [CrossRef]
- Islam, M.S.; Driscoll, D.J.; Fisher, C.A.J.; Slater, P.R. Atomic-Scale Investigation of Defects, Dopants, and Lithium Transport in the LiFePO4 Olivine-Type Battery Material. Chem. Mater. 2005, 17, 5085–5092. [Google Scholar] [CrossRef]
- Fisher, C.A.J.; Hart Prieto, V.M.; Islam, M.S. Lithium Battery Materials LiMPO4 (M = Mn, Fe, Co, and Ni): Insights into Defect Association, Transport Mechanisms, and Doping Behavior. Chem. Mater. 2008, 20, 5907–5915. [Google Scholar] [CrossRef]
- Perera, D.; Ganeshalingam, S.; Kuganathan, N.; Chroneos, A. A Computational Study of Defects, Li-Ion Migration and Dopants in Li2ZnSiO4 Polymorphs. Crystals 2019, 9, 563. [Google Scholar] [CrossRef] [Green Version]
- Kaushalya, R.; Iyngaran, P.; Kuganathan, N.; Chroneos, A. Defect, Diffusion and Dopant Properties of NaNiO2: Atomistic Simulation Study. Energies 2019, 12, 3094. [Google Scholar] [CrossRef] [Green Version]
- Kuganathan, N.; Gkanas, E.I.; Chroneos, A. Mg6MnO8 as a Magnesium-Ion Battery Material: Defects, Dopants and Mg-Ion Transport. Energies 2019, 12, 3213. [Google Scholar] [CrossRef] [Green Version]
- Kuganathan, N.; Kordatos, A.; Chroneos, A. Defect Chemistry and Li-ion Diffusion in Li2RuO3. Sci. Rep. 2019, 9, 550. [Google Scholar] [CrossRef] [Green Version]
- Streltsov, S.; Skorikov, N. Spin-state transitions in CaFeSi2O6 and NaFeSi2O6 under pressure. Phys. Rev. B 2011, 83, 214407. [Google Scholar] [CrossRef]












| Parameter | Calculated | Experiment [13] | |∆|(%) | ||
|---|---|---|---|---|---|
| Force Field | DFT | Force Field | DFT | ||
| a (Å) | 9.8716 | 9.9900 | 9.8107 | 0.62 | 1.83 |
| b (Å) | 8.9569 | 8.9373 | 8.9856 | 0.32 | 0.54 |
| c (Å) | 5.2459 | 5.2256 | 5.2245 | 0.41 | 0.02 |
| α = γ (°) | 90.00 | 90.00 | 90.00 | 0.00 | 0.00 |
| β (°) | 105.16 | 104.01 | 104.59 | 0.54 | 0.56 |
| V (Å3) | 447.7095 | 452.6849 | 445.7081 | 0.45 | 1.56 |
| Defect Process | Equation Number | Defect Energy (eV) | Defect Energy (eV)/Defect |
|---|---|---|---|
| Ca Frenkel | 1 | 9.92 | 4.96 |
| Fe Frenkel | 2 | 9.74 | 4.87 |
| Si Frenkel | 3 | 18.36 | 9.18 |
| O Frenkel | 4 | 5.74 | 2.87 |
| Schottky | 5 | 38.40 | 3.84 |
| CaO Schottky | 6 | 5.94 | 2.97 |
| FeO Schottky | 7 | 6.72 | 3.36 |
| SiO2 Schottky | 8 | 14.28 | 4.76 |
| Ca-Fe anti-site (isolated) | 9 | 0.90 | 0.45 |
| Ca-Fe anti-site (cluster) | 10 | 0.86 | 0.42 |
| Ca-Si anti-site (isolated) | 11 | 9.06 | 4.53 |
| Ca-Si anti-site (cluster) | 12 | 5.26 | 2.63 |
| Fe-Si anti-site (isolated) | 13 | 5.98 | 2.98 |
| Fe-Si anti-site (cluster) | 14 | 2.84 | 1.42 |
| Migration Path | Ca-Ca Separation (Å) | Activation Energy (eV) |
|---|---|---|
| A | 4.47 | 4.36 |
| B | 5.02 | 4.49 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuganathan, N.; Chroneos, A. Defects and Dopants in CaFeSi2O6: Classical and DFT Simulations. Energies 2020, 13, 1285. https://doi.org/10.3390/en13051285
Kuganathan N, Chroneos A. Defects and Dopants in CaFeSi2O6: Classical and DFT Simulations. Energies. 2020; 13(5):1285. https://doi.org/10.3390/en13051285
Chicago/Turabian StyleKuganathan, Navaratnarajah, and Alexander Chroneos. 2020. "Defects and Dopants in CaFeSi2O6: Classical and DFT Simulations" Energies 13, no. 5: 1285. https://doi.org/10.3390/en13051285
APA StyleKuganathan, N., & Chroneos, A. (2020). Defects and Dopants in CaFeSi2O6: Classical and DFT Simulations. Energies, 13(5), 1285. https://doi.org/10.3390/en13051285