1. Introduction
During design, operation, and troubleshooting of various process and power equipment-containing tube bundles, it often is important to know the velocity and temperature fields in both the tube and the shell sides. These are obtained predominantly using Computational Fluid Dynamics (CFD) models and, therefore, articles covering a wide range of such applications are available. For example, Wei et al. [
1] discussed a coupled CFD-Lagrange multipliers optimization method for flow distribution adjustments to prevent freezing of power generation natural draft cooling systems during winter operation. Chien et al. [
2], on the other hand, presented a coupled CFD-surrogate-based optimization of flow distribution in a heat exchanger inlet header. Zhou et al. [
3] focused on CFD investigation and optimization of a compact heat exchanger comprising a single row of tubes, and Łopata et al. [
4] published an article covering the experimental investigation of flow distribution in a similar cross-flow heat exchanger, but with a tube bank consisting of elliptical tubes. CFD evaluation and optimization of solar collectors, commonly also using a single row of risers, were discussed, for instance, by García-Guendulain et al. [
5], who aimed to improve the collector performance by changes of riser-to-header cross-sectional area and diameter ratios. Karvounis et al. [
6] carried out a numerical and experimental study of the flow field in a forced circulation Z-type flat plate solar collector. Articles focusing on two-phase flow are also common. Li et al. [
7] studied flow reversal in vertically inverted U-tube steam generators used in marine nuclear power plants, whereas Klenov and Noskov [
8] investigated the effect of two-phase flow pattern in an inlet duct on flow distribution in the upper part of a trickle bed reactor. As for dispersion headers, which are often used in flue gas cleaning equipment, a CFD investigation of the impacts of inlet flow rate, hole diameter, and downstream distance on the flow distribution in an annular multi-hole header was presented by He et al. [
9]. Other frequent research areas where the knowledge of flow distribution is critical are fuel cells and micro-channel heat exchangers. One might mention, e.g., the CFD and laser Doppler velocimetry investigation of flow distribution in a polymer electrolyte membrane fuel cell stack by Bürkle et al. [
10], the CFD evaluation of pressure and flow distribution effects on the performance of polymer electrolyte membrane fuel cells by Heck et al. [
11], or the CFD optimization of a liquid cooling system of a power inverter in an electric vehicle presented by Hur et al. [
12]. Various studies involving liquid-cooled micro-channel heat sinks for electronics are quite common as well. See, e.g., the article by Li et al. [
13] discussing the optimization of the micro-channel topology.
Studies not utilizing CFD are much less common and, typically, focus on evaluations of the respective equipment via physical experiments. To name just a few, one could mention the experimental investigation of flow distribution and its effect on the performance of a plate-fin heat exchanger by Zhu et al. [
14], the study of two-phase refrigerant distribution in a finned-tube evaporator by Tang et al. [
15], or the article by Quintanar et al. [
16] covering natural circulation flow distribution in a multi-branch manifold. Micro-channel equipment was discussed, e.g., by Yih and Wang [
17], who carried out an experimental investigation of the thermal-hydraulic performance of a micro-channel heat exchanger for waste heat recovery, or by Lugarini et al. [
18], who focused on the evaluation of flow distribution uniformity in a comb-like micro-channel network. On the other end of the size spectrum are heat exchanger networks, in which Ishiyama and Pugh [
19] studied thermo-hydraulic channeling in the individual parallel branches. In their paper, they also presented a model for prediction of flow distribution in the branches for the case when no flow control was implemented. Similarly, Novitsky et al. [
20] discussed multilevel modeling and optimization of large-scale pipeline systems using specialized software tools. In these two studies, however, modelling of pressure drop was only done in a simplified manner. Korelstein [
21], on the other hand, discussed mathematical properties of classical hydraulic network flow distribution problems which included pressure-dependent closure relations. An essentially identical problem can also be encountered when it comes to the design of water distribution networks. Still, proper inclusion of pressure drop in the respective models is rare because they generally focus on layout optimization while meeting the local water demands (see, for instance, the article by Cassiolato et al. [
22], who proposed a Mixed-Integer Nonlinear Programming (MINLP) model for this purpose), identification of sources of contamination (as done, e.g., using a convolutional neural network by Sun et al. [
23]), detection of leakage points (see, for example, the article by Fang et al. [
24]), evaluation of the network performance and reliability (as discussed, e.g., in the Hanoi case study by Jeong and Kang [
25]), etc.
To the best of the authors’ knowledge, there currently is no semi-accurate but fast Finite Element Analysis-based model of fluid flow other than [
26] that would properly include the pressure drop. This model, however, does not consider heat transfer and, thus, is of limited practical value to the designers of process and power equipment. Consequently, CFD models, because of their significant computational cost, are being employed for evaluations of fluid flow distribution and heat transfer only if absolutely necessary. As a result, the corresponding temperature fields, which, to a large degree, depend on mass flow rates through individual tubes, are also unknown. This may not pose significant problems if thermal stress is relatively even throughout the tube bundle in question. Nonetheless, mechanical failures of bundles, stemming from improper design procedures which a priori assume uniform flow distribution, are not uncommon when it comes to heat exchangers featuring large changes in stream temperatures. The present paper, therefore, introduces a significantly extended version of the flow-only, adiabatic model discussed in [
26]. This includes heat transfer between the fluids in the tube and the shell sides of a cross-flow tube bank heat exchanger (e.g., an economizer) as well as various other improvements. Shell-side flow was modelled as unidirectional. As test cases, a simple cross-flow tube bundle heat exchanger from the literature and an existing heat recovery hot water boiler, for which the necessary data had been provided by its operator, were considered. These were compared to the results obtained using the present model and, to gain further insight, also to the data from an industry-standard heat exchanger design software package. A good agreement among the data sets was observed.
2. Materials and Methods
The original model discussed in [
26] assumed adiabatic flow, that is, no heat transfer was allowed on the walls of the parallel flow channels in the distribution system. The model was shown in the same article to provide data with relative errors of at most 4% compared to detailed transient CFD simulations even in the case of highly turbulent flows. Such accuracy was achievable due to the relative simplicity of the flow systems for which the respective model has been intended (e.g., tube bundles in heat recovery steam generators). The overall conclusion, therefore, was that, in terms of application in preliminary analyses of selected heat transfer equipment or for shape optimization of the mentioned equipment, the model was suitable for engineering practice.
Because of the nature of the model, its performance in case of laminar flow was a priori expected to be acceptable. Although several tests were carried out earlier even with low total mass flow rates to make sure this really was the case, no example was given in [
26]. To remedy this, let us mention, for instance, one of the test flow distribution systems (see
Figure 1) used in the original article and the respective laminar flow distribution data and relative errors. For convenience’s sake, parameters of the flow system are listed in
Table 1. The obtained mass flow rates are compared in
Figure 2a, while
Figure 2b shows the corresponding relative errors. It can be seen that the error values generally were in a ±1% band with only two of them being at around 1.2%. Relative errors obtained using other test flow systems were of similar magnitudes. Thus, one could conclude that, in the case of laminar flow, the accuracy was even better than when the flow was highly turbulent.
2.1. Inclusion of Heat Transfer into the Model
The main shortcoming of the original, flow-only version of the Finite Element Analysis (FEA)-based model was its inability to properly evaluate tube bundles in which heat transfer could not be neglected. Given the intended purpose of the model (that is, usage in engineering practice), this functionality had to be implemented.
Please note that heat transfer was not, strictly speaking, evaluated using FEA. However, the temperature fields in the tube side and the shell side were still obtained using a system of linear equations generated as shown in the following text, and this system was then solved in the usual manner. It was assumed that the temperature profile between two end nodes of an edge was continuous and was given by the mean temperatures on control volume cross-sections, which were perpendicular to the corresponding edge. The iterative solver then worked similarly to any other segregated solver. First, the fluid flow (FEA-based) submodel was solved under the assumption of a constant temperature field. Next, the heat transfer submodel was solved under the assumption of a constant velocity field. This was followed by the update of the fluid physical properties and other necessary post-iteration tasks, and then the fluid flow submodel was solved again. This iterative procedure was repeated until convergence was reached.
Even though the heat transfer submodel was not using FEA, the corresponding mesh on which the temperature field was calculated can be constructed in a similar manner. In the fluid flow mesh, the field to be calculated was described by total pressures in the nodes. The temperature field can be described analogously with the difference being that every edge had its own temperature in the node.
Figure 3 shows the two meshes and the differences between meshes.
As mentioned before, the temperatures were calculated using a set of linear equations. From
Figure 3 it is clear that a flow system consisting of
n edges will feature 2
n node temperatures and, therefore, 2
n linear equations were required. There were three classes of temperature-related equations that were used in the model:
Flow mixing and splitting,
Heat transfer through channel walls, and
Boundary conditions.
2.1.1. Flow Mixing and Splitting
When, in an arbitrary mesh node, streams
q1,
q2, …,
qm are mixed into a single stream
j, we can write
Here, denotes the mass flow rate of the qth stream, cp,q the specific heat capacity, and Tj and Tq the corresponding stream temperatures. Each specific heat capacity should be taken as the mean value obtained for the corresponding temperature range [Tj, Tq].
If, on the other hand, a single stream
j is split into streams
r1,
r2, …,
rn, the outflow temperature is the same for all these streams, and the respective
n equations are
In some systems, there may be blind edges with zero mass flow rate. The temperatures in the nodes of these edges are calculated as if the edges were of the regular type featuring outflow (see also the schematic in
Figure 4).
In a general case with streams q1, q2, …, qm being mixed and then split into streams r1, r2, …, rn, one will get one Equation (1) governing the resulting outflow temperature Tj and (n − 1) Equation (2), that is, (n − 1) identities for the remaining outflow temperatures. The total number of equations governing the mixing/splitting in the node will, therefore, be equal to number of outflow streams.
2.1.2. Heat Transfer through Channel Walls
Let us have two meshes representing the tube and the shell sides of a heat exchanger and focus on an arbitrary pair of adjacent control volumes representing a portion of the tube side (i.e., a tube segment) and the enclosing portion of the shell side (see
Figure 5). Let
,
cp,t,
Tt,1, and
Tt,2 denote the tube side mass flow rate, mean specific heat capacity at constant pressure, and inlet and outlet temperatures and
,
cp,s,
Ts,1, and
Ts,2 the corresponding shell-side quantities.
Should, e.g., the hot fluid be placed in the shell side, then the overall heat balance could be written as
Let us for a moment assume that the temperature of the fluid in the shell-side control volume is constant and is equal to the shell-side inlet temperature,
Ts,1. Let us also assume that the tube-side inlet temperature,
Tt,1, is known. Additionally, let
L denote the length of the tube-side mesh edge and
U the cumulative overall heat transfer coefficient. The heat flux for a small portion of this edge having the length d
x can then be expressed as
This can be modified, rearranged, and written in integral form,
which yields
From Equation (6), we immediately see that the temperature at the end of the edge can be obtained using
Equation (7) must be linearized for it to be used in a matrix solver. This is done in a straightforward manner by taking
where the necessary cumulative overall heat transfer coefficient,
U, is computed from the tube-side and shell-side heat transfer coefficients. These, in turn, are calculated using equations from literature (e.g., [
28] in the case of plain tubes or [
29] if the tubes are finned) depending on the actual bundle geometry and flow conditions. Additional information regarding validation of the commonly used empirical equations for estimation of heat transfer coefficient in the case of plain and serrated fins can be found, for instance, in [
30]. One could also use the correlations from [
31], which have been obtained via the machine learning technique. If U-shaped or helical fins of various types are employed, then the two-part article by Hofmann and Heimo [
32,
33] can be recommended to the reader. The final, linearized equation for a single edge, therefore, is
Considering the shell-side outlet temperature, for cross-flow with
Ts,1 = const. on the entire inlet face of the control volume, we have
Just as before, this can be modified and rearranged to yield
The mean shell-side outlet temperature then is
which corresponds to the shell-side outlet temperature obtained using the respective set of linear equations.
One could also simplify the model even further by using a one-dimensional shell-side mesh (i.e., a mesh such that each cross-section of the shell along the general flow direction is spanned by just one cell). With a row of
n tubes being present in a specific shell-side cell, Equation (3) would simply become
while Equation (7), still necessary for each of the
n tubes, would remain almost identical:
There also is a special case of no heat transfer, which can be treated similarly. The necessary equation can easily be obtained by setting the heat transfer coefficient in Equation (14) to zero, which results in the equation being reduced to the equality between the temperatures in the end nodes of an edge. This is important because the number of linear equations describing heat transfer is always constant no matter if heat transfer occurs or not.
2.1.3. Boundary Conditions and the Complete System of Linear Equations
Up to this point, every equation was simply describing some relationship between the node temperatures. For a steady state problem to be completely specified, some temperatures must be known. However, let us first analyze the number of equations available thus far. For a fluid flow system with n edges and m inflow streams, there are 2n unknown temperatures. We can get n equations from the heat transfer. The following n − m equations can be obtained from stream mixing in the nodes. The remaining m equations must be provided via boundary conditions, i.e., inlet temperatures must be specified for each of the inflow stream (other arrangements may be possible in selected cases). When there are multiple fluid flow systems connected by heat transfer equations, the number of available equations remains the same.
2.1.4. Coupling of the Flow Distribution and Heat Transfer Submodels
Each major iteration of the FEA-based solver consists of two steps. The first step is a fixed temperature field analogy of the adiabatic model (as described in [
26]; robustness of the model can be improved by carrying out this first step repeatedly until the respective residual falls below a predefined threshold). New estimates of the temperature fields for both the tube and the shell sides are then obtained in the second step. Here, the necessary values of
CU are updated using edge mass flow rates from the first step and the corresponding new estimates of cumulative overall heat transfer coefficients. To solve the respective combined linear system for the tube-side and the shell-side temperatures, one boundary temperature must be provided for each stream (for instance, at the inlet of each tube in the bundle and for each inlet cell in the discretized shell side). The resulting temperature matrix could look, for example, like the one in
Figure 6. Even though linear systems represented by such matrices can be solved quite easily, it is obvious from the figure that implementation of a reordering algorithm would be necessary should one want to improve performance via preconditioning in case of much larger linear systems.
As the convergence criterion, the fluid flow submodel used the scaled norm of the difference between the solutions from the predictor step and the corrector step. The corresponding scaled residual limit was 10−5. In the case of the heat transfer submodel, if we denote the original linear system Ax = b, then the scaled residual norm is computed from b − Ax just before the heat transfer submodel is solved. (If it were done after the respective solution process, the norm would be equal to zero.) The same residual limit, that is, 10−5, was used here.
All physical property data (mean specific heat capacity, dynamic viscosity, etc.) are always taken for the current conditions from the IAPWS [
34] or the CoolProp [
35] physical property libraries, or, in special cases (e.g., flue gas), are computed using various interpolation functions or tabulated data depending on the actual compositions. Thermal properties of the tube and fin materials are always obtained using tabulated data from literature (for example, from the technical standard [
36]).
2.2. Shell-Side Pressure Drop
Similarly to heat transfer coefficients, pressure drop in the shell side cross-flow tube bundle is calculated via well-known empirical equations from, e.g., [
37]. The actual formula to be used depends on the bundle geometry, possible presence of fins, etc.
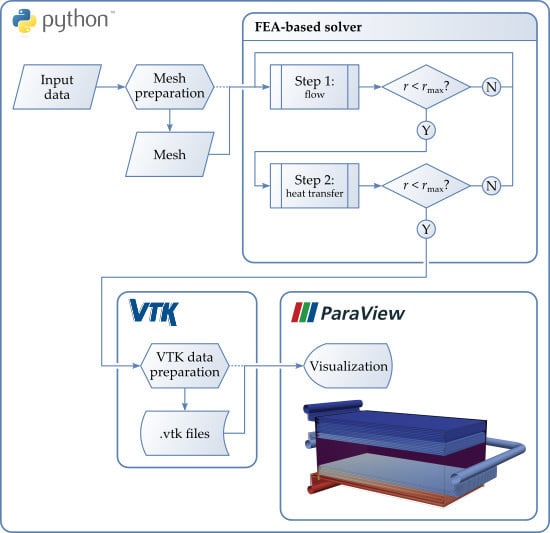
2.3. The Developed Computer Code
The computer code was developed in Python [
38] and utilized NumPy [
39] to carry out the necessary matrix computations. The Visualization Toolkit (VTK) [
40] and meshio [
41] libraries were used to export solution data to Kitware ParaView [
42] for visualization. Although no graphical user interface (GUI) is available yet, the authors plan to add it in the future, for example, via the Django web framework [
43]. Please note that the code is not publicly available.
Apart from the inclusion of heat transfer, many additional improvements of the code have been made since the publication of the initial article discussing the FEA-based model [
26]. The most important one probably is parallelization of the mass flow rate corrector step (please see [
26] for details). As the correction algorithm was carried out independently for each mesh edge, a set of asynchronous workers was created using the standard Python multiprocessing library, and the correction tasks were processed in batches on all available CPU cores. This then results in much shorter computational times. Parallelization of the internal matrix computations, however, was not implemented because, given the numbers of elements in the simplified meshes, the matrices were rather small. In other words, the CPU time saved by parallel solution would be wasted on auxiliary operations needed to split the task to multiple cores, thus rendering the net improvement either negligible or even negative.
4. Discussion
The results yielded by the present model and by HTRI Xchanger Suite for the air-to-water heat exchanger from the literature have shown that even though an apparatus can be decomposed into parts for which correlations or calculation procedures for heat transfer coefficients and pressure losses may exist, successfully applying them may not be straightforward. The main reason is that such procedures require local fluid and material properties, and these generally depend on the temperature and pressure, that is, quantities which the designer is trying to calculate. This is where the present model steps in. The data have also highlighted the facts that the accuracy of any model depends to a large degree on the quality of equations utilized for the calculation of the various coefficients and that further research in this area is, therefore, necessary. Additionally, one can draw the conclusion that using averaged values for the entire tube side and shell side can lead to notable differences. In the case of the outlet temperatures in this air-to-water heat exchanger, it was up to ca. ±7%.
As for the heat recovery hot water boiler, the most important stream parameters are listed in
Table 7. It can be seen that the tube-side outlet temperature and pressure drop were better predicted by HTRI Xchanger Suite, while the accuracy of the shell-side outlet temperature and pressure drop predictions was higher in the case of the present model. Overall, the accuracy of the model was deemed acceptable concerning its intended purpose.
A significant advantage of the model over the industry-standard design package offered by HTRI (or other commonly used heat transfer equipment design packages) lies in the fact that it provides detailed data on the tube-side fluid flow and temperature distributions. This information can be of great value when trying to prevent certain types of operating problems (e.g., excessive thermal loading of the tubes in the bundle and the subsequent mechanical failures). Another advantage is that in the case of cross-flow tube bundles (the primary target application of the present model), HTRI Xchanger Suite assumes that mixing of tube streams occurs after each pass, even if this may not actually be true. Such a simplification may increase convergence, but it also may diminish local effects and, therefore, introduce errors into the data.
5. Conclusions
The point of this research was not to develop a replacement to the universally applicable, commercial heat transfer equipment design packages, such as HTRI Xchanger Suite. On the contrary, the goal was to create a simplified model for heat exchangers representable using sets of interconnected 1-D meshes, which are typically used in high-temperature (i.e., heat recovery) industrial applications and are prone to suffer from operating problems. The model, once finished, should be fast, yet accurate enough, and should provide estimates of not only the flow distribution in the bundle and the tube- and shell-side temperature fields but also the resulting mechanical stress field in the bundle caused by uneven thermal loading. In other words, the aim was to have a supplementary tool which would enable the designer to evaluate in advance, and without any significant effort or time spent, the thermal-hydraulic behavior of the mentioned heat exchangers as well as the likelihood of them suffering mechanical failures under the design operating conditions. In this regard, the FEA-based modelling approach seems to be promising, but a lot of work, as well as a thorough validation, are still needed before it is ready for production use.
The comparison with HTRI was mentioned in this paper solely to present the current capabilities of the model in terms of heat transfer prediction. The discrepancy (or at least a part of it) was very likely caused by the heat transfer coefficients and the hydraulic resistance coefficients being calculated differently. However, the model was designed in such a way that it can easily incorporate any standard method for calculating these coefficients for the simple 1-D mesh elements. More complex flow systems can then be built from these simple elements and the solution strategy remains the same, which ensures scalability of the model.
Considering the fact that shell-side flow velocity fields commonly are not uniform, one of the possible future improvements of the FEA-based model could lie in strictly using a grid of cells in the shell side (in the plane perpendicular to the general direction of flow) instead of only one cell. Another enhancement, which the authors plan to implement, is to make it possible to interface the current computer code with other simulation codes. This would enable the evaluation of flow systems in which some parts are more complex and, therefore, not directly compatible with the simplified mesh elements used by the FEA-based model.