Selection of Artificial Lift Methods: A Brief Review and New Model Based on Fuzzy Logic

Abstract

Artificial lift methods have applications in oil wells where oil production is no longer possible due to natural reservoir energy, so this necessary energy is added by introducing lift methods. In order to achieve optimum production, the selection of an artificial lift method is very important. This paper uses fuzzy logic as a mathematical and conceptual model for selection of the optimal artificial lift method. The outcome or IF-THEN rules, as the central part of the model, is based on empirical data from the selected oil fields. Results are presented in two ways: according to the surfaces of irregular geometric bodies, and their gravity with the scattering of results, i.e., on smaller and greater possibilities of interpreting results when there are small differences in outputs. Finally, a sensitivity analysis of the model is presented.

1. Introduction

Oil wells begin production by the primary drive mechanisms under the influence of natural reservoir energy. When the primary energy depletes, artificial lift methods are applied. The most common of these are: gas lift (GL), sucker rod pumps (SRP), electric submersible pumps (ESP), progressive cavity pumps (PCP), and hydraulic jet type pump (HP) [1].

The selection of the artificial lift method is one of the most important process for achieving economically efficient production. Choosing the optimal method is done by taking into account the parameters of reservoir and fluids, well type, environmental conditions, and economic factors (capital and operational costs).

Final decisions on artificial lift methods are often made based on the following subject criteria:

• These should satisfy the individual requirements of the manufacturer and company
• Selected methods are acceptable to operations managers.

In order to choose the optimal method, a large number of criteria must be taken into account for the purpose for associate an appropriate level of significance to define a synthetic estimate. In this type of selection of the optimal artificial lift method, approaches based on the model of multiatributive and multi-criteria analyses are used, as well as those based on statistical data processing from engineering practice and expert systems.

The selection of artificial lift methods was initially performed by experts who consider all the parameters of the well and the reservoir, as well as the limitations and advantages of applying the individual method. With the advancement of computer techniques based on the considered parameters, expert systems were created, i.e., programs that help select an appropriate method (Optimal pumping unit search—OPUS, Sistema Experto de Levantamiento Artificial—SEDLA). Decision-making methods, such as the decision tree and the most recent multi-criteria analysis (Technique for Order Preference by Similarity to Ideal Solution—TOPSIS, Elimination Et Choix Traduisant He realite—ELECTRE, Simple Additive Weighting—SAW and VišeKriterijumska Optimizacija i Kompromisno Rešenje—VIKOR), have also been applied.

In practice, there is no general model and standard for the selection of artificial lift methods, but each oil company uses an expert system, i.e., programs, or tables with defined application limits for each method. The conventional methodology for selecting an appropriate artificial lift method is the process of defining and analyzing different criteria, considering the general advantages and disadvantages of each method. By developing technologies in the petroleum production, the limits of the applicability of artificial lift methods are constantly moving, which affects the conditions for their application.

The theory of fuzzy sets and, in general, fuzzy logic is a conceptual and mathematical tool for modeling different processes dominated by uncertainty, multidimensionality, subjectivity and indeterminacy. Optimization criteria were taken into account during model development in order to achieve an optimal selection of artificial lift methods by fuzzy logic application. Optimization criteria are well utilization and service ability. Fuzzy logic has a great application, used in many engineering disciplines as a decision-making tool. In the field of petroleum engineering it is applied in several areas: Reservoir Porosity Estimation [2,3]; Oil Separation [4]; Hydraulic fracturing [5].

2. Brief Overview of the Techniques for Selecting Optimal Artificial Lift Methods

Several authors have been involved in development of techniques for selecting optimal artificial lift methods.

In 1981, Buford Neely and a group of authors published summaries of panel discussions on the topic of Selection of an Artificial lift Method. Each of the 5 experts processed a single theme that formed one section of this work. They analyzed the possibility of application, advantages, disadvantages and limitations of some artificial lift methods (SRP, ESP, HP, GL). Buford Neely presented considerations on the reservoir and the well; Fred Gipson presented the SRP; Joe Clegg covered the topic of a gas-lift; Bill Capps described ESP; and Phil Wilson explained the HP [6].

As the main factors geographical and environmental restrictions were taken, the secondary factors were reservoir pressure, productivity index, the characteristics of reservoir fluids, and well productivity characteristics. The importance of this work is reflected in the fact that for the first time the limits of the application of artificial lift methods as well as their advantages and disadvantages were defined in one place [6].

In 1988, E.P. Valentin and F.C. Hoffmann developed a smart integrated Optimal pumping unit search system (OPUS) for the selection of artificial lift methods. OPUS has the ability to control the technical and financial aspects of the selection of artificial lift methods. The was based on the characteristics of each artificial lift method, the basic value of investments, and maintenance costs and equipment, using a specific computer algorithm [7].

In 1988, Joe Dunn Clegg dealt with the problem of selecting artificial lift methods and considered income, operational and investment costs as criteria. This author considered that the optimal method chosen should achieve the highest production at the lowest operating costs. The paper describes the methods of exploitation of oil with all their characteristics and the limitations of application in exploitation [8].

In 1994, Espin, D.A. et al. used the SEDLA expert system for the selection of artificial lift methods. This contains three modules: a module of expert knowledge, experience and theoretical knowledge; a simulation design module; and an economic evaluation module.

The expert knowledge module consists of an expert knowledge base, i.e., the knowledge of nine world-recognized experts from certain fields of artificial lift methodology and the ways in which they choose the best artificial lift method, generally known theoretical (textbook) knowledge, and basic, commonly-used calculations. The design simulation module serves to design the methods selected in the previous module. The results of this module show the performance of the well for the selected individual method [9].

The module of economic evaluation uses detailed designing equipment, surface and underground equipment, energy supply, and previously determined optimal production to calculate the profitability of each method. The calculations used are standard project evaluation parameters: net present value, internal rate of return etc., and include investment costs as well as repair and maintenance costs [9].

In 1995, Lloyd R. Heinze and a group of authors used a “decision tree” to choose artificial lift methods, where the main factor was long-term economic analysis. Other factors that influence the evaluation of the method are operational costs, primary investments, costs during the working life and energy efficiency. Three steps were taken through the decision tree in order to reach a decision. The first step narrows the selection, based on technical limitations of the methods applied. The parameters considered are: pump volume capacity, the depth in combination with the desired dynamic pressure at the bottom of the well, the deviation of the well, and characteristics of the reservoir. The second step further reduces the choice, based on secondary technical limitations, such as temperature limitations, operator training, availability of the main source of energy, fluid, surface conditions (space limitations, noise, visibility, safety), and additional limitations at the bottom of the well (high gas-liquid ratio—GLR, scale, sand, corrosion). The third step is the economic parameters of technically applicable methods. For each candidate method, the present value of the investment during the life of the well is calculated, taking initial costs, energy costs, repair costs and maintenance. The cost comparison is based on wells and on the oil field. Costs are: investment costs, service costs, repair costs, additional personnel costs, energy costs, maintenance costs, stop costs, inventory costs, and general costs. Finally, considering the outcome of each step on the tree, a final choice is made by considering subjective items that cannot be easily quantified [10].

The process of selecting an ideal method for exploitation is complex and subjective. Different researchers can choose different methods using the same facts and information. There is, however, a process of thinking that everyone can follow to eliminate some subjectivity. Mehrdad Alemi, with a group of authors [11,12,13,14], dealt with the selection of artificial lift methods using several models of multicriteria analysis: TOPSIS, ELECTRE, SAW and VIKOR, in the case of oil fields in Iran. The authors used multiple sets of input data: restrictions on production, deposits and wells; characteristics of production fluid, and surface infrastructure.

Cross-Sectional Analysis of Presented Research

In 1981, Neely tackled defining the limit values for the parameters of artificial lift method application. The priority was his technical parameters, while the economic impact was less important [6].

In 1988, Clegg used an analysis of all boundary conditions for the application of exploitation methods, but gave priority to economic parameters [8].

In 1988, Valentin and Hoffman created the OPUS Expert System program, which apart from the parameters of methods and characteristics of the well and reservoir, also takes into account economic aspects (costs) [7].

In 1994, Espin and a group of authors observed technical characteristics and then economic ones [9].

In 1995, Heinze and a group of authors use the decision tree to apply group criteria in several steps. The first two steps used technical constraints, while in the third step only economic parameters were considered, i.e., costs [10].

In 2010, 2011, and 2013 Alemi and a group of authors used three sets of data for their models: production, reservoir and well limitations; characteristics of production fluid; and surface infrastructure. All data were technical parameters; economic parameters were not considered [11,12,13,14].

Input parameters can be grouped into three groups:

• Characteristics of reservoir, well and fluid (depth, pressure, production, and technical limitations of artificial lift methods)
• Conditions in which the well operates (location, availability of energy, training of people, etc.)
• Economic factors (capital costs, operating costs, and maintenance costs.)

Selection methods can be divided according to the mode of operation in three groups (

Table 1. Group of parameters by selection method.

Selection Method	First Group	Second Group	Third Group
Neely [6]	x	x
Valentin [7]	x	x	x
Clegg [8]	x	x	x 1
Espin [9]	x 1	x 1	x
Heinze [10]	x	x	x
Alemi [11,12,13,14]	x	x

¹ priority.

):

The first group (I) represents methods that use all limitations on the characteristics of the well, reservoir, fluid and working conditions, as technical limitations of artificial lift methods. The expert reviews all the parameters and decides which is the best method [6,8,10,15].

The second group (II) is expert systems: these are programs that analyze all parameters, both technical and economic, and in the output give the best artificial lift method. They use expert knowledge; it is necessary for an expert to analyze the output of the program and decide which method is most appropriate [7,9].

The third group (III) of methods are those of optimizing the selection of artificial lift methods. These are the models created by applying multi-criteria analysis (TOPSIS, ELECTRE, SAW and VIKOR). Based on the known parameters, the expert gives estimates of the input data for the optimization model, and the output is the most suitable artificial lift method [11,12,13,14].

The analysis of the mathematical and conceptual models indicates that:

• there are several input parameters (I, II, III);
• for the first and third groups, parameters are measurable and can be displayed numerically;
• In the second group, parameters are from different processes dominated by uncertainty, multidimensionality, subjectivity, and indeterminacy, and can only be displayed expertly.

In order to form the optimization model, it is necessary to reduce the indicated parameters to the same form in the analytical sense and to find a synthesis model.

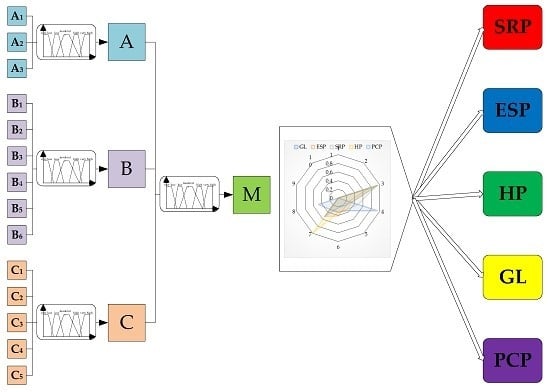
3. Development of a Conceptual Model for the Selection of an Artificial Lift

Parameters that define the optimal method are considered in three structural groups:

• Infrastructure parameters (A), which relate to (A1) energy forms and energy sources, (A2) automatic regulation and utility management, and (A3) service;
• Physical-geological parameters (B) respectively: (B1) depth, (B2) oil production, (B3) temperature, (B4) fluid density, (B5) viscosity, and (B6) well deviation;
• Production operating problem parameters (C), which are: (C1) corrosion, (C2) solid particles, (C3) gas oil ratio—GOR, (C4) paraffin, and (C5) water cut.

Figure 1 shows the conceptual model of an expert system for optimized selection of an artificial lift method evaluation on the base of fuzzy interferences of the input data.

Parameters (B and C) are exact data and are measurable, while (A) parameters can be presented according to the experience of employees at the well site and can only be shown by linguistic descriptions. The model must have an analytical part, looking at all input parameters within the reference values (

Table 2. Characteristics and limitations of the application of artificial lifting methods [16].

Operating Parameters	SRP	ESP	HP	Gas Lift	PCP
Typical operating depth (m)	35–3828	348–3480	1740–3480	1740–3480	696–1566
Maximum operating depth (m)	5568	5220	5220	5220	2088
Typical operating volume (m3/d)	0.8–267	18–5343	53–712	18–1781	0.89–392
Maximum operating volume (m3/d)	1069	7124	2672	5343	801
Typical operating temperature (°C)	38–177	38–135	38–121	38–121	24–66
Maximum operating temperature (°C)	288	204	260	204	121
Corrosion handling	Good to Excellent	Good	Excellent	Good to excellent	Fair
Gas handling	Fair to good	Fair	Good	Excellent	Good
Solids handling	Fair to good	Fair	Good	Good	Excellent
Fluid gravity (kg/m3)	>1014.34	>1000	>1014.34	>965.85	<849.85
Maximum wellbore Deviation	0–90 deg landed pump	0–90 deg	0–90 deg <79 deg/100 m	70 deg, short to medium radius	0–90 deg <49 deg/100 m
Servicing	Workover or pulling rig	Workover or pulling rig	Hydraulic or wireline	Wireline or workover rig	Workover or pulling rig
Prime mover	Gas or electric	Electric motor	Multi-cylinder or electric	Compressor	Gas or electric

), and a synthesis part, input parameters, reduced into one. It is evident that the model is rife with uncertainty, indeterminacy, multidimensionality, and relativity. The model must have an inference engine. The new mathematical and conceptual model of optimized selection is descripted in the following text by steps.

3.1. Analysis of the Input Parameters

In the part of the model relating to analysis, the most important step is the fuzzy proposition. This is a procedure for representing a statement that includes linguistic variables based on available information about the considered engineering system [17]. A definition of structure and interdependence of linguistic variables is carried out in a coordinate system of membership function (μ), with regard to j-class as a synonym of measurement for the observed phenomena.

Regarding the number of linguistic variables, seven has been found to be the maximal number of rationally recognizable expressions that a human can simultaneously identify [18]. Therefore, the accepted value of linguistic variables for representing M performances is five (Figure 2). The five necessary defined linguistic variables (i.e., fuzzy sets) are: very low, low, moderate, high, and very high. The expert assessment consists of linguistic variables and the extent to which they apply to the observed well.

In dependence of μ, fuzzy number (FN) can be presented in form (1):

FN = (μ j = 1, … μ j = 10)

(1)

Linguistic variables (H) can be presented in the same form. For example, if H = Very low, µ = 1 for j = 1, 2; µ = 0 for j = 3, ..., 10.

Other fuzzy sets can be written as:

• low = (0/1, 0/2, 1/3, 1/4, 0.33/5, 0/6, 0/7, 0/8, 0/9, 0/10)
• moderate = (0/1, 0/2, 0/3, 0.5/4, 1/5, 1/6, 0.5/7, 0/8, 0/9, 0/10)
• high = (0/1, 0/2, 0/3, 0/4, 0/5, 0.33/6, 1/7, 1/8, 0/9, 0/10)
• very high = (0/1, 0/2, 0/3, 0/4, 0/5, 0/6, 0/7, 0/8, 1/9, 1/10)

Input parameters can be displayed by three indicators (A, B, and C). These indicators are synthesized into one (M) (Figure 3).

Parameter A1 represents the form and source of energy. Grades are given depending on which form of energy is used, how close the source of this energy is, and the possibility of using other sources of energy. According to this proposition, the phasing sets are defined in the following way and presented to the analyst:

A1 = {very low level of availability of energy without substitution; low availability with the possibility of partial substitution; medium level of availability, with the possibility of complete substitution on request; high level of energy availability with occasional predictable shortages; very high availability, without the need for any additional investment}.

Parameter A2 represents the level of automatic regulation and automatic control. Grades are given depending on the existence of automatic regulation and management and the possibility of applying them.

A2 = {complete manual control; dominantly manual with automated individual operations; semi-automatic; dominantly automatic with secondary manual controls; fully automated}.

Parameter A3 represents maintenance (maintainability). It contains supportability and design predispositions for maintenance. Grades are given depending on the geographical position of the well and the well characteristics themselves, i.e., the possibility of quick and easy servicing of problems in the well.

A3 = {spare parts, tools, and people fully dislocated, maintenance on demand; corrective maintenance present; corrective and service maintenance; planned preventive maintenance; proactive maintenance}.

Parameter B1 considers depth. The values of the depth of the well are translated into estimates based on the limit values of the optimal and maximum depth of the well. Each of the observed artificial lift methods has a recommended depth.

Parameter B2 represents the production. Based on the optimal and maximum amount of fluid that each of the observed artificial lift methods can produce, the greater the amount of fluid produced, the fewer the methods can be applied. Based on this value of production is translated into grades.

Parameter B3 represents the temperature. Based on the optimal and maximum fluid temperature at which each of the observed artificial lift methods can be applied, the higher the temperature of the fluid, the fewer the methods that can be applied.

Parameter B4 represents the density of the fluid. The values of fluid density are translated into grades based on the distribution of oil by density [19]:

light—0.85; medium heavy 0.85–0.93; heavy 0.93–1.00; very heavy 1.00–

The B5 parameter is viscosity. The viscosity values of the fluid are translated into grades based on the distribution of hydrocarbons viscosity (relative) [19]:

condensates 0.5–1; gasoline 0.6; kerosene 2; light oil 2–100; heavy oil 100–1000

Parameter B6 represents well deviation. With the increase in the angle of deviation of the well, the number of artificial methods that can be used is reduced.

Parameter C1 represents corrosion. With the increase in the proportion of compounds that may increase corrosion, the number of artificial methods that can be used decreases in the production fluid.

Parameter C2 represents solid particles. With the rise of solid particles in the production fluid, the number of artificial methods that can be used is reduced.

Parameter C3 represents GOR. With the increase in the gas factor in the production fluid, the efficiency of artificial methods, which can be used, decreases, except in the case of GL where an increase in GOR has a positive effect on the operation of the system.

Parameter C4 represents paraffin. With the increase in the amount of paraffin in the production fluid, the number of artificial methods that can be used is reduced.

Parameter C5 represents water cut. With the increase in water in the production fluid, methods that can produce larger quantities of fluid are more widely used.

3.2. Synthesis Part of the Model

The synthesis of partial indicators (A, B, C) into one (M) is performed by fuzzy composition, which is a model that provides the structure of indicators-influencing M performance. In other words, if the influence indicators A, B and C are presented as fuzzy numbers [20], their composition provides a fuzzy number which represents M. Max-min composition is often used in fuzzy algebra as a synthesis model [18,21,22,23,24].

Synthesis is performed on two levels. In the first, parameters A1, A2, A3 are synthesized in A, respectively B1 to B6 in B, and C1 to C5 in C. At the second level of synthesis, A, B and C parameters are synthesized into the M (Figure 4).

The goal of this synthesis is to give a solution of optimization model. For example, if A1 is medium, A2 is high, A3 is low, B1 is very high, B2 is very low, B3 is low, B4 is low, B5 is very high, B6—low, C1—very high, C2—very low, C3—very high, C4—very high, C5—low, a GL method is obtained.

Partial indicators of optimal method of selection, A, B and C, are presented as membership function μ:

A = (μ_A¹,…, μ_A^j,…, μ_Aⁿ); B = (μ_B¹,…, μ_B^j,…, μ_Bⁿ); C = (μ_C¹,…, μ_C^j,…, μ_Cⁿ);

(2)

M assessment is obtained in the form:

• μ_M = (MAX_j=1, …, MAX_j=10) = (μ_M¹, …, μ_M¹⁰)

where:

• MAX_j = max{MIN_o}, for every j
• and MIN_o = min{μ_A^{j = 1, …, 10}, μ_B^{j = 1, …, 10}, μ_C^{j = 1, …, 10}}, for all o = 1 to O.

The size O represents the outcome, which is defined for each possible combination of input parameters. The outcome is defined on the basis of empirically defined IF-THEN rules. As input data (

Table 3. Input data range for forming the model [25,26,27].

Parameters	Value	Unit
depth	506–3500	m
oil production	1.5–2340	m3/day
temperature	50–180	°C
oil density	810.89–1014.34	kg/m3
oil viscosity	2–681	mPas
well deviation	0–35	°
share of corrosive substances	0–5	%
solid particle content	0–16	%
GOR	10–458	m3/m3
paraffin share	0–20	%
water content	0–93	%
forms of energy and source	8–9	grade
possibility of service	5–7	grade
possibility of automatic regulation and remote control	4–9	grade

) for the developed model were taken data from different oilfields in Serbia, Libya, Azerbaijan and Iran. Based on the data entered for many different wells, a graphical output for each method is obtained in the form of geometrically irregular shapes (maps). Overlapping of shapes for individual method represents wells in which methods can be equally applied.

By entering new wells in the developed model, results are compared with existing maps of artificial lift methods. The greatest percentage overlap with some of the artificial lift methods represents the best solution for a new well.

4. Application of Conceptual Model for the Selection of an Artificial Lift Method at the Test Well

GL oil well in Salman oil field in Iran has been chosen as a test well. The Salman oil field data are given in

Table 4. Salman oil field input data [12].

Parameters	Value	Unit
Production, Reservoir and Well constraints
production rate	178	m3
well depth	2438.4–3352.8	m
casing size	0.36576	m
dogleg severity	0–10/0.3048	m
temperature	82.22–98.89	°C
flowing pressure	>68.95	bar
completion	simple
recovery method	secondary waterflood
Produced Fluid Properties
water cut	70	%
fluid viscosity	<0.1	Pas
corrosive fluid	no
sand and abrasives	<10	ppm
GOR	650	m3/m3
VLR	<0.1
Surface Infrastructure
location	offshore
electrical power	utility
well service	pulling unit

.

Selection of mentioned method was done using an optimization model based on a multi-criteria analysis, specifically using the ELECTRE method [12]. The exploitation methods for application adequacy were ranked as output of the model (Figure 5). The most commonly used methods for exploiting the analyzed field are the estimated GL method (grade 0), ESP (grade 1), followed by HP (grade 2) and finally PCP and SRP (grade 3).

Data from the Salman oil field are included in model M, described in the previous section, and results are given in Figure 6. Figure 6 shows the radar coordinate system with marked areas. Areas representing each exploitation method depending on μ are in radial direction and j in a circular direction. Each of the five commonly used methods (GL, ESP, SRP, HP, PCP) defines a specific surface that is standard. The level of overlapping the surface, which represents the result for the new well and some of the standard surfaces, represents the level of applicability of the standard method for the conditions of the new well. Figure 6a shows the standard of all methods. In Figure 6b–f is given an indication of the applicability of individual standard methods with a new well. The overlap level can be expressed in percentages (

Table 5. Percentage of overlapping of 5 surfaces of oil exploitation method with new well.

Method	Overlapping of Each Method with New Well (%)
GL	80.35
SRP	54.28
ESP	43.91
HP	49.03
PCP	40.70

).

Based on graphic and analytical results, it can be seen that the GL method is in first place, i.e., it is the most applicable for the case under consideration to the extent of 80.35%. The other 4 methods are applicable in the range of 40–55%.

It is obvious that the parameters delineating the standard methods of exploitation are quite close, except for the ESP method. The problem of frequent overlaps that are close to each other can be solved if the results are displayed in a coordinate system that involves the center of mass (weighted mean of maximum) and the mathematical deviation (Figure 7).

Center of mass

By calculating the weighted mean of maximum, defuzzification is done and the value of the class is obtained, together with the fuzzy set which the result obtained belongs to. The weighted average value is calculated according to the following equation [28,29]:

$$Z=\frac{{{\displaystyle \sum }}_{i=1}^{10}{\mu }_i{x}_i}{{{\displaystyle \sum }}_{i=1}^{10}{\mu }_i}$$

(3)

where:

• x_i—the support value at which its membership function reaches a maximum value (for trapezoidal membership functions this is taken as the center of the maximal range); μ_i—the degree of truth of its membership function

Standard deviation

$$S=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^{i=N}{\left(x_i-x_{sr}\right)}^2}{N-1}}$$

(4)

where:

• N—number of experiments
• x_i—observed values
• x_sr—mean value of all observations based on Equations (3) and (4)

The center of mass and standard deviation are calculated for each of the model results. The standards of artificial lift methods were obtained by summing together many wells with good results from applying the appropriate method. For each summed surface, we calculated the center of mass and standard deviation (

Table 6. Center of mass and standard deviation values for each of the standards.

Artificial Lift Method	Center of Mass	Standard Deviation
GL	6.0258	0.3861
SRP	4.4314	0.3122
ESP	6.9750	0.3086
HP	5.0320	0.3901
PCP	4.5774	0.3128
New well	6.1590	0.3410

).

Figure 7 shows that the position of new wells close to the position of the standard for method GL, with a slight tilt towards the ESP method.

The sensitivity of this model is performed, based on the intensity of the change in input parameters for the new well and the intensity of change in the results. For the output result Z to move to the ESP standard, the changes of input parameters are to the extent of 10% under the indicators A and C, while the parameter changes under indicator B are 25%. In the case where Z moves to the SRP standard, it is necessary to measure from −20% of the parameters under indicator B, while the remaining parameters remain unchanged. Sensitivity is determined with the change of parameters for a following percentages: −20, −15, −10, 10, 15 and 20.

By changing the parameters under a certain indicator, A, B and C, the existing model output for the new well can be switched to the method standards (

Table 7. The percentage of changes in the parameters of the new well.

A	B	C	Methods
30	20	10	GL
0	−20	0	SRP
−10	25	−10	ESP
−10	−20	−20	HP
−15	0	0	PCP

).

The sensitivity of the model for input parameters change for −10% and +10% is presented in Figure 8.

According to the diagram (Figure 8), if the parameters increase, the center of gravity moves to the right. When the parameters are reduced, the center of gravity moves to the left of the diagram. The uneven shift of the focus to the left side of the diagram is due to a considerable number of parameters being at the limit values (1 or 10).

5. Conclusions

This paper presents the optimization model for the selection of an artificial lift method based on fuzzy logic. Unlike the conventional multi decision analysis models for choosing the artificial lift method, the proposed model reduces subjectivity in defining priorities during the selection process of the model’s input parameters.

The model can be widely used because artificial lift standards can be created specifically for each oil field. Based on the parameters of the wells for which the artificial lift method is being selected, it is possible to choose the set of data that is most similar to them. In this way, the optimal artificial lift method can be determined even more precisely.

The results are presented in two ways that include the surfaces of irregular geometric area and their center of mass with standard deviation. The first presented method gives results in percentage of surface overlapping for 5 oil exploitation method in comparison with new well resulting surface. The second method gives results that involves the center of mass (weighted mean of maximum) and the mathematical deviation. The application of second method is recommended in case when it is difficult to interpret the results by first method.

The created model was confirmed using the example of the Iranian Salman field, where the result confirmed that the GL is the most appropriate method of exploitation. A comparison with the previous result for the mentioned oil field was made. This comparison shows that the results match completely.