In-Situ Measurement of Power Loss for Crystalline Silicon Modules Undergoing Thermal Cycling and Mechanical Loading Stress Testing

Abstract

An in-situ method is proposed for monitoring and estimating the power degradation of mc-Si photovoltaic (PV) modules undergoing thermo-mechanical degradation tests that primarily manifest through cell cracking, such as mechanical load tests, thermal cycling and humidity freeze tests. The method is based on in-situ measurement of the module’s dark current-voltage (I-V) characteristic curve during the stress test, as well as initial and final module flash testing on a Sun simulator. The method uses superposition of the dark I-V curve with final flash test module short-circuit current to account for shunt and junction recombination losses, as well as series resistance estimation from the in-situ measured dark I-Vs and final flash test measurements. The method is developed based on mc-Si standard modules undergoing several stages of thermo-mechanical stress testing and degradation, for which we investigate the impact of the degradation on the modules light I-V curve parameters, and equivalent solar cell model parameters. Experimental validation of the method on the modules tested shows good agreement between the in-situ estimated power degradation and the flash test measured power loss of the modules, of up to 4.31 % error (RMSE), as the modules experience primarily junction defect recombination and increased series resistance losses. However, the application of the method will be limited for modules experiencing extensive photo-current degradation or delamination, which are not well reflected in the dark I-V characteristic of the PV module.

1. Introduction

Monitoring the degradation of photovoltaic (PV) modules during accelerated stress testing is crucial for understanding the degradation kinetics of the PV modules. Moreover, accurate module power loss data with high temporal resolution is necessary for developing accelerated PV degradation models for predicting PV module lifetime in the field. However, often times, the accelerated tests have to be interrupted, for the PV modules to be characterized on Sun simulators and their power loss measured [1]. This limits the number of intermediate module power degradation measurements that can be acquired in practice, and is a time-consuming process in itself. Therefore, in-situ (semi) continuous module degradation monitoring methods are necessary.

In-situ module monitoring methods have been developed for different types of accelerated stress tests, stress factors and degradation parameters. Module moisture monitoring during accelerated aging tests for PV module encapsulants, was proposed by Carlsson et al. [2], by integrating a moisture sensor inside thin-film modules. Tanahashi et al. [3] proposed in-situ monitoring of AC impedance parameters of PV modules undergoing rapid thermal cycling stress tests, for detecting solder bond failures after prolonged test cycles. A method for monitoring module degradation during dynamic mechanical load testing, was proposed by Bosco et al. [4], by forward biasing the PV module with a small sinusoidal voltage signal and measuring the differential conductance, and was used to determine the occurrence of ribbon failure and the cycle/time-to-failure. More advanced PV characterization methods, such as electroluminescence (EL) imaging were also implemented for in-situ monitoring of PV module degradation during mechanical load stress testing [5], as well as integrated into the environmental test chamber, for monitoring of modules undergoing combined accelerated stress testing [6].

Monitoring the module’s maximum power ($P_{max}$) at Standard Test Conditions (STC: 1000 W/m², 25 °C, AM 1.5) during stress testing, is especially important for accelerated stress testing, as it is the reference condition for reporting PV module efficiency and performance parameters. Such a method was previously developed by Hacke et al. [7], for in-situ monitoring the STC $P_{max}$ degradation of crystalline silicon (c-Si) PV modules undergoing voltage stress testing and experiencing shunting type potential-induced degradation (PID-s). The method is based on translating dark current-voltage (I-V) curves acquired in-situ, at 25 °C, from the first to the fourth I-V quadrant. This was achieved by superposition of the dark I-Vs with the module’s short circuit current ($I_{sc}$), determined at the beginning of the test. Later, a method was developed for estimating STC $P_{max}$ degradation, due to PID-s, from the dark I-V curves measured in-situ at the stress temperature (typically 60 °C or 85 °C), without the need to ramp down the test chamber temperature to 25 °C [8,9].

Estimation of the PV module’s STC $P_{max}$ degradation from dark I-V measurements was possible because the PID-s mechanism in c-Si modules largely manifests by fill-factor loss due to increasing junction recombination (2nd diode pre-exponential, $J_{o2}$) and decreasing shunt resistance ($R_{sh}$) [7], which impact both the dark I-V and light I-V characteristics in similar proportions. However, STC $P_{max}$ estimation by dark I-V superposition is limited [10] if delamination, increased series resistance ($R_s$) or photo-current degradation occurs, which affect the light I-V characteristic primarily. Other degradation mechanisms impact the dark and light I-V characteristics of the PV module differently, therefore the dark I-V based STC power estimation method, needs to be to account for degradation of the other solar cell parameters associated with the degradation mode.

Modules undergoing thermo-mechanical stress and cell breakage may undergo $J_{o1}$ increases due to increased unpassivated surface area at fracture surfaces, $R_s$ losses due to metallization breaks and solder bond failure [11,12], $J_{o2}$ and junction ideality factor increases, and shunt resistance decreases due to increased physical defects penetrating the junction [13]. Additionally, some fraction of the cell circuit may be removed when the cell and its metallization become electrically disconnected [14].

To study these compound degradation modes and develop an in-situ power loss estimation method, modules underwent mechanical loading, thermal cycling and humidity-freeze cycles to impart mechanical damage, during which dark I-V curves and STC flash tests were obtained, and used in equivalent solar cell diode model analysis of the degradation. Thereafter a method is developed for estimating STC power loss in three steps: (i) estimate the effects of shunting and $J_{o2}$ recombination losses by superposition of the dark I-V curves with the initial STC $I_{sc}$ to the first quadrant, and rough estimation of the STC $P_{max}$ (ii) estimate $R_s$ and $J_{o1}$ losses from the dark I-V slope at high current, and correct the rough STC $P_{max}$ estimation; and (iii), correct the STC power estimates obtained during the course of degradation, based on module flash testing at the end of the stress test - to include effects of additional series resistance losses observed with illumination, $J_{o1}$ recombination losses, and current mismatch losses. This is achieved by matching the final dark I-V curve-determined $P_{max}$ to the final flash-test-determined STC $P_{max}$, and adjusting the intermediate power loss estimates accordingly.

2. Experiment and Module Degradation Analysis

Four new conventional 60-cell multi-crystalline silicon (mc-Si) PV modules of the same design were subjected to five rounds of stress consisting of 2400 Pa static mechanical loading, $-40$ °C to 85 °C thermal cycling (TC), and $-40$ °C to 85 °C at 85% RH humidity freeze (HF) cycling stress to various extents. The initial (new) state of the modules, along with the five subsequent stages of stress applied to the modules are designated with roman numerals (I-VI) and further detailed in

Table 1. Description of the experiment stages.

Stage	Description
I	Four new mc-Si modules characterized at STC
II	Static mechanical loading with 2400 Pa
III	29 cycles of TC and 4 cycles of HF
IV	18 cycles of HF
V	Static mechanical loading with 2400 Pa
VI	13 cycles of HF

. The number of stress cycles were determined primarily through trial and error and repeatedly stressing and characterization of the modules, with the goal of inducing a progressive degradation of the modules, as well as noticeable power loss.

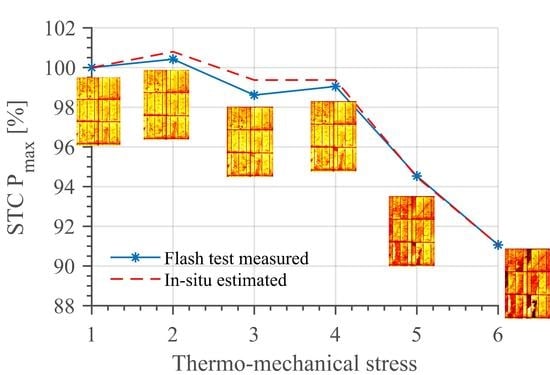
The degradation of module #1 can be observed in the EL images of the module shown in Figure 1, where the new state of the module is shown in Figure 1a, whereas the subsequent mechanical degradation of the module’s cells is shown in Figure 1b–f. EL images showing the degradation of modules #2–#4 are shown in Appendix A.1, in Figure A1, Figure A2, Figure A3 respectively.

After each stress-test stage, the modules were flash tested under STC and low irradiance conditions (LIC, 200 W/m², 25 °C). The STC and low light $P_{max}$ degradation is summarized in Figure 2. Here we observe a final STC power degradation between 8% and 10.4 %, and between 5.5 % to 7 % LIC power loss.

The corresponding light I-V curves for module #1 are shown in Figure 3a, where we can observe fill factor and short-circuit current losses to a lower extent. Whereas, the dark I-V characteristics of module #1, shown in Figure 3b, show changes in both the high and low current regions of the dark I-V curve, associated with increased series resistance [15] and shunt and recombination losses [16], respectively. The electrical characteristics and power loss of modules #2–#4 are shown in Appendix A.2, Figure A4, Figure A5, Figure A6 respectively.

By examining the STC I-V curve parameters, we observe that the STC $I_{mp}$, summarized in Figure 4 for all four modules, contributes the most to the module performance degradation, which can be attributed primarily to the partial solar cell cracks, that increase the cells series resistance. Whereas a small decrease in $I_{sc}$ can be observed for module #1, and to a lesser extent in modules #2 and #3, which can be attributed to a reduced photo-current generating cell area, due to fully disconnected cell cracks.

In addition, the modules show $V_{mp}$ voltage losses in the later stages of the experiment (V and VI), shown in Figure 5, whereas the $V_{oc}$ does not change significantly. Considering that the $V_{mp}/V_{oc}$ ratio decreases in these stages as well, we can deduce that these losses are caused (at least in part) by an increase in series resistance [17].

To further understand the modes of degradation associated with this type of stress, we analyze the equivalent solar cell parameters of the modules during degradation [18]. To achieve this we fit the dark I-V curves ($I_{dark}-V_{dark}$) of the modules taken after each experiment stage to the two-diode solar cell model (1), often used for dark I-V based solar cell diagnostics [15]:

$$J=J_{o1}\left\{exp\left[\frac{q(V-J{R}_s)}{n_{1}kT}\right]-1\right\}+J_{o2}\left\{exp\left[\frac{q(V-J{R}_s)}{n_{2}kT}\right]-1\right\}+\frac{V-J{R}_s}{R_{sh}},$$

(1)

where J is the current density; V is the terminal voltage; $n_1$ and $n_2$ are the diode ideality factors; $R_s$ and $R_{sh}$ are area-specific series and shunt resistance parameters, respectively, of the solar cell; T is the cell temperature; k is the Boltzmann constant; and q is the elementary charge.

The effect of the module degradation on the equivalent solar cell model parameters is summarized in Figure 6. From these results, we can confirm a substantial increase in module series resistance $R_s$, previously observed in the I-V parameters and caused by partial solar cell cracks and metallization breaks [14]. Moreover, from Figure 6 we can observe a significant increase in the $n_2$ and $J_{o2}$ diode model parameters, suggesting solar cell junction degradation and recombination losses occurring in the junction. Lastly, the $n_1$ and $J_{o1}$ diode model parameters increase to a lesser extent. This increase can be attributed here to increasing defects and unpassivated surfaces at the cell cracks, causing increased surface and bulk recombination losses.

Concluding on the analysis of the diode model parameters, we can group the power loss mechanisms into three categories: (i) shunting and $J_{o2}$ recombination losses, (ii) series resistance losses, (iii) other losses including $J_{o1}$ recombination losses, current mismatch losses, and a decrease in photo-current generation due to cell fracturing. In the next section we aim to estimate these failure modes’ effect on the module STC power loss separately.

3. In-situ STC Power Loss Estimation Method

3.1. Step 1—In-Situ during Stress Testing—Estimate the Effects of Recombination and Shunting Losses

The first step, estimating the power loss due to shunting and $J_{o2}$ recombination losses, has been previously studied for crystalline silicon modules undergoing PID-s [7,19]. In this case, module STC $P_{max}$ degradation can be estimated with high accuracy in-situ, by superposition of the dark I-V curve with measured $I_{sc}$ [7]. Some limitations of the method include modules that are severely shunted, for which the $I_{sc}$ current starts to decrease significantly [20] and superposition using the initial $I_{sc}$ is no longer valid.

We assume that module dark I-V characteristics are measured at 25 °C during the test. This is a feasible assumption for mechanical loading tests that are carried out at room temperature, as well as for thermal cycling and humidity freeze type tests, where the 25 °C dark I-V characteristic can be measured at the beginning/end of the cycle, when the chamber and module temperatures are ramped up/down.

Based on the 25 °C dark I-V curve we can estimate the module STC $P_{max}$ that accounts for the effects of shunting and $J_{o2}$ losses, by superposition of the dark I-V curve with $I_{sc}$, and calculating the maximum power point $P_{max\_SUP}\left(t\right)$ from the resulting I-curve, as expressed in (2):

$$P_{max\_SUP}=max\left\{\left[I_{dark}\left(t\right)+I_{sc}\left(t_0\right)\right]V_{dark}\left(t\right)\right\},$$

(2)

where $I_{dark}\left(t\right)-V_{dark}\left(t\right)$ is the dark I-V characteristic of the module measured measured at 25 °C and at a time point t during the stress test, and $I_{sc}\left(t_0\right)$ is the initial STC $I_{sc}$ current of the module measured on a Sun simulator.

3.2. Step 2—In-Situ during Stress Testing—Estimate (Partial) Series Resistance Losses from Dark I-V Measurements

In the next step we need to estimate the increase in series resistance due to cell cracks, from the dark I-V measurements acquired in-situ, and use it to correct the superposition estimated power loss $P_{max\_SUP}$ accordingly. This could be achieved by curve fitting the diode model parameters ($R_s$) in (1), which requires careful parametrization of the initial conditions and does not lend itself to automatic analysis during the stress test.

Alternatively, increases in the module’s dark series resistance can be estimated from the slope of the dark I-V curve at high current ($R_{s\_DIV}$), as in (3), which is linearly related to the module’s $R_s$, not including diode-internal voltage drops [21].

$$R_{s\_DIV}=\frac{\mathrm{d}{V}_{dark}}{\mathrm{d}{I}_{dark}}{|}_{I=max\left(I_{dark}\right)}.$$

(3)

Next, to estimate the power loss due to the increased series resistance, we start from the empirical equations for calculating the effect of increased series resistance on the fill factor of solar cells [22], defined in (4):

$$F{F}_s=F{F}_0\left(1-1.1r_s\right)+\frac{r_s^2}{5.4},$$

(4)

where $r_s$ is the normalized PV module series resistance, $F{F}_0$ is the fill factor without the effect of series resistance, and $F{F}_s$ is the corrected PV module fill factor, including series resistance losses.

If we consider $r_s$ to only represent the increase in the module’s series resistance since the test has started ($t_0$), we can define as a function of $R_{s\_DIV}\left(t\right)$, determined in-situ, and the initial STC parameters of the module: $I_{mp}\left(t_0\right)$ and $V_{mp}\left(t_0\right)$, as in (5):

$$r_s\left(t\right)=\left[R_{s\_DIV}\left(t\right)-R_{s\_DIV}\left(t_0\right)\right]\frac{I_{mp}\left(t_0\right)}{V_{mp}\left(t_0\right)}.$$

(5)

Finally, we can consider $F{F}_0$ to represent the fill factor corresponding to the maximum power estimation without the effect of increased series resistance $P_{max\_SUP}$. By rewriting (4) in terms of maximum power, we calculated the $R_s$ corrected power loss estimation $P_{max\_DIV}$, as in (6)

$$P_{max\_DIV}\left(t\right)=P_{max\_SUP}\left(t\right)\left[1-1.1r_s\left(t\right)\right]+\frac{r_s{\left(t\right)}^2}{5.4}{V}_{oc}\left(t_0\right)I_{sc}\left(t_0\right).$$

(6)

3.3. Step 3—Adjustment with Final Light I-V Curve—Estimate the Total Series Resistance and Other Losses from a Final STC Flash Test

There are two limiting factors for estimating series resistance from the dark I-V characteristic of the PV module that must be considered. First, when measuring the dark I-V characteristic, the current paths through the module are more limited in area compared to when the module is illuminated [23]. This situation leads to two different module $R_s$ values, dark and light measured, where generally the dark-measured $R_s$ is be smaller than the light-determined resistance. Consequently, use of the dark I-V curve-determined series resistance, such as $R_{s\_DIV}$, will underestimate the STC $P_{max}$ losses due to increases in $R_s$. Second, $R_{s\_DIV}$ does not explicitly include the effect of decreased current generation and mismatch due to cell fracturing or the increase in $J_{o1}$ recombination losses that can appear around $max\left(I_{dark}\right)$ in the dark I-V curve and can lead to additional errors in estimating the STC $P_{max}$.

To compensate for the limitation of the dark estimated series resistance, in the final step $R_{s\_DIV}$ is adjusted such that the final $P_{max}$ degradation, which is estimated from dark I-V measurements, matches the final STC $P_{max}$ degradation that is measured by a Sun simulator. This problem can be formulated for solution as in (7), where $t_0$ and $t_f$ are the initial and final 25 °C dark I-V curve and STC power ($P_{max\_STC}$) measurements points:

$$\frac{P_{max\_DIV}(R_{sx},t_f)}{P_{max\_DIV}(R_{sx},t_0)}=\frac{P_{max\_STC}\left(t_f\right)}{P_{max\_STC}\left(t_0\right)}.$$

(7)

By numerically solving (7) for $R_{sx}$, we can determine a $R_{sx}=R_{s\_Match}\left(t_f\right)$ value, which will account for both the increase in module (light) $R_s$, as well as other losses, such $J_{o1}$ recombination and current mismatch losses due to cell fracturing, occurring in the module after the previous experiment stage. The $R_{s\_Match}$ is then used to adjust each intermediate $R_{s\_DIV}\left(t\right)$ with (8):

$$R_{s\_DIV\_Scaled}\left(t\right)=R_{s\_DIV}\left(t\right)\frac{R_{s\_Match}\left(t_f\right)}{R_{s\_DIV}\left(t_f\right)}.$$

(8)

Finally $R_{s\_DIV\_Scaled}\left(t\right)$ is replaced in (5) and (6) to calculate $P_{max\_DIV\_Scaled}\left(t\right)$, which will match the final STC $P_{max}$ degradation value and estimate the module degradation throughout the stress test more accurately.

4. Results and Discussion

We experimentally evaluate the accuracy and limits of the in-situ power loss estimation procedure, by comparing the PV module power losses determined in the three steps of the proposed method, with measured module power loss.

First we determine the extent of power loss due to shunting and $J_{o2}$ losses, by calculating $P_{max\_SUP}$ from (2), using the $I_{sc}$ measured at at 1000, 600, and 200 W/m² irradiance, and 25 °C. The relative change in $P_{max\_SUP}$ of module #1 is shown in Figure 7, versus the Sun simulator measured power of the module, denoted as $P_{max\_LIV}$, under the same irradiance conditions. We can observe that the dark I-V superposition-based power loss estimation is poor, especially under high irradiance conditions and extensive degradation (up to 6% difference in relative power loss). This can be explained by the increased series losses that are not captured by the superposition method.

Similar trends can be observed by comparing STC $P_{max\_SUP}$ of the other module samples with their measured $P_{max\_LIV}$ shown in Figure 8. As the modules degrade more by cell cracking, the estimation error increases. We can surmise that the shunting and $J_{o2}$ losses amount to up to 2% of the absolute power loss, explaining up to 30% of the power loss exhibited.

Next, to evaluate the extent of increased series resistance losses, we determine the increase in $R_{s\_DIV}$ from 25 °C dark I-V measurements and use it to estimate the relative module power loss ($P_{max\_DIV}$), according to (5) and (7). Figure 9 shows the estimated power loss $P_{max\_DIV}$ for module #1. It can be observed that the estimation has improved only slightly, however at 5% STC $P_{max}$ degradation (stage V), $P_{max\_DIV}$ underestimates the module #1 degradation by 3% (absolute error), whereas at 10% module degradation (stage VI), the difference between the dark vs. light measured module power degradation can be as much as 5% (absolute error). This is explained by the limited capability of $R_{s\_DIV}$ to characterize the light series resistance, as well as the impact of $I_{sc}$ losses on the module STC power.

Similar estimation errors are observed for the other modules shown in Figure 10, with the exception of module #3, which is closest to the ideal estimation line. One possible explanation is that module #3 had the least $I_{sc}$ losses among the four modules tested, as can be observed from Figure 4.

The module power loss estimation must be improved by the final STC $P_{max}$ adjustment, as in (7) and (8), which will compensate for most of the current mismatch, decrease in $I_{sc}$ and photocurrent-generation, and other losses such as $J_{o1}$ recombination losses, which are difficult to characterize from the dark I-V curve alone. These findings are consistent with previous research on methods for estimating PV module series resistance [24], that have concluded that dark series resistance underestimated the light determined series resistance by more than 50%, in most cases [24].

To exemplify the adjustment procedure, we used the initial and final STC flash test $P_{max}$ to calculate the correction factor $R_{s\_Match}$ from (7), and use it to adjust the dark I-V-determined series resistance ($R_{s\_DIV}$) as in (8). The resulting $R_{s\_DIV\_scaled}$ as well as $R_{s\_DIV}$ are compared in Figure 11, with the STC flash test determined resistance of module #1, calculated after each stress stage. As can be observed, stages V and VI show a significant increase in the module’s series resistance that is not captured by $R_{s\_DIV}$, but can be compensated for, by the final STC flash test, and thus included in $R_{s\_DIV\_Scaled}$.

Finally, $P_{max\_DIV\_Scaled}$ is calculated by substituting $R_{s\_DIV\_Scaled}$ in (6), and is compared with the STC measured $P_{max}$ in Figure 12. As can be observed, this approach leads to a more successful estimation of the module degradation, especially in the later stages of the experiment.

The errors between the $P_{max\_DIV\_Scaled}$ and STC $P_{max}$ in the early stages of degradation result from the approximation that $R_{s\_DIV}$ scales linearly with the light series resistance, assumed in (8). Second, flash test and dark I-V measurement errors are compounded, such that individual points in Figure 12 may be affected. Despite these limitations, if we compare the root-mean-square error (RMSE) between the STC measured $P_{max}$, and the dark I-V estimated $P_{max}$, as in

Table 2. Comparison of root-mean-square error (RMSE) between the STC measured $P_{max}$, and the dark I-V estimated $P_{max}$ ($P_{max\_SUP}$ – only shunting and $J_{o2}$ losses are estimated; $P_{max\_DIV}$—series losses are estimated as well; $P_{max\_DIV\_Scaled}$—other losses are estimated with a final STC power match).

Module	RMSE [%]
	${\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x}\mathbf{\_}\mathit{S}\mathit{U}\mathit{P}}$	$P_{\mathit{m}\mathit{a}\mathit{x}\mathbf{\_}\mathit{D}\mathit{I}\mathit{V}}$	${\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x}\mathbf{\_}\mathit{D}\mathit{I}\mathit{V}\mathbf{\_}\mathit{S}\mathit{c}\mathit{a}\mathit{l}\mathit{e}\mathit{d}}$
#1	3.42	2.65	0.37
#2	4.31	3.48	1.13
#3	3.22	2.13	1.06
#4	3.77	2.92	0.83

we can observe the final adjustments of the series resistance based on flash testing, and reduce the total estimation error by 3–6 times.

5. Conclusions

Tools and methods for monitoring PV module degradation, in-situ, during accelerated stress testing, are important for understanding the degradation kinetics and developing reliability and accelerated degradation modules, as well as for reducing the cost, duration and effort of accelerated stress tests.

In this regard, in-situ acquired dark I-V curves have previously been used to successfully monitor PID-s during voltage stress testing of c-Si PV modules, and were the basis of the in-situ monitoring method proposed in this work. However monitoring thermo-mechanical induced degradation of PV modules by dark I-V measurements is more challenging, due to the complex nature of the induced degradation modes. Namely, thermo-mechanical stress can compound several failure modes: micro-cracking, partial or complete cell cracking and disconnection, cell interconnect failure, and even delamination. These will affect cells in the modules to different extents, and are sometimes difficult to deconvolute from module level I-V characteristics or by equivalent solar cell model parameters, as the basic assumption of identical cells in the module is broken.

Part of the power loss caused by cell cracking—corresponding to shunting and junction recombination, can be estimated by superposition of the dark I-V with initial module short-circuit current, similar to the in-situ PID power loss estimation method. However, the majority of power loss caused by cell cracking is caused by an increase in the module’s distributed series resistance, which is not well captured by the dark I-V curve superposition method.

As was shown, part of the module’s increased series resistance can be estimated from the dark I-V characteristic, however, not completely. A final STC IV measurement, at the end of the stress test, is necessary to correct the dark I-V power loss estimation. However, module delamination and short-circuit current degradation, occurring during the stress test, will reduce the estimation accuracy of the in-situ method, for intermediate points of degradation. Therefore, for longer thermo-mechanical stress tests, intermediate flash tests would be necessary to correct the power loss estimation in these cases, or another in-situ measurement that is able to characterize degradation of the module’s photo-current generation properties.