Degradation-Conscious Equivalent Consumption Minimization Strategy for a Fuel Cell Hybrid System
Abstract
:1. Introduction
2. Fuel Cell/Battery Hybrid System Modeling
2.1. System Configuration
2.2. Fuel Cell System Model
2.3. Battery Model
2.4. Driving Load Model
2.5. Traction System Model
3. Energy Management Strategy
3.1. Rule-Based Strategy
3.2. The Equivalent Consumption Minimization Strategy (ECMS)
3.3. Degradation-Conscious Equivalent Consumption Minimization Strategy (D-ECMS)
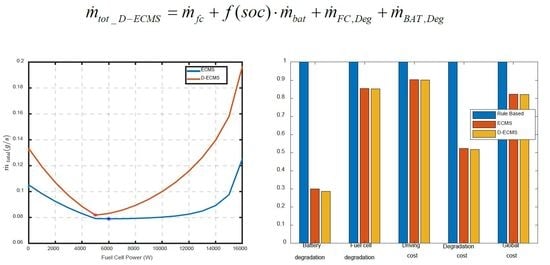
4. Simulation and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Xin, Q.; Pinzon, C.F. Improving the environmental performance of heavy-duty vehicles and engines: Particular technologies. In Alternative Fuels and Advanced Vehicle Technologies for Improved Environmental Performance, 1st ed.; Folkson, R., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 279–369. [Google Scholar] [CrossRef]
- Ahluwalia, R.K.; Wang, X.; Rousseau, A.; Kumar, R. Fuel economy of hydrogen fuel cell vehicles. J. Power Sources 2004, 130, 192–201. [Google Scholar] [CrossRef]
- Fletcher, T.; Thring, R.; Watkinson, M. An Energy Management Strategy to concurrently optimize fuel consumption & PEM fuel cell lifetime in a hybrid vehicle. Int. J. Hydrogen Energy 2016, 41, 21503–21515. [Google Scholar] [CrossRef] [Green Version]
- Chan, C.C. The State of the Art of electric, Hybrid, and Fuel Cell Vehicles. Proc. IEEE 2007, 95, 704–718. [Google Scholar] [CrossRef]
- Xu, L.F.; Li, J.Q.; Hua, J.F.; Li, X.J.; Ouyang, M.G. Optimal vehicle control strategy of a fuel cell/battery hybrid city bus. Int. J. Hydrogen Energy 2009, 34, 7323–7333. [Google Scholar] [CrossRef]
- Paganelli, G.; Guezennec, Y.; Rizzoni, G. Optimizing Control Strategy for Hybrid Fuel Cell Vehicle. In Proceedings of the SAE 2002 World Congress, Detroit, MI, USA, 4–7 March 2002. [Google Scholar] [CrossRef]
- Sciarretta, A.; Guzzelle, L. Control of hybrid electric vehicles. IEEE Control Syst. Mag. 2007, 27, 60–70. [Google Scholar] [CrossRef]
- Manzie, C.; Grondin, O.V.; Sciarretta, A.; Zito, G. ECMS Controller Robustness in Flex-Fuel Hybrid Vehicles. J. Dyn. Syst. Meas. Control 2014, 136, 064504. [Google Scholar] [CrossRef]
- Panday, A.; Bansal, H.O. A Review of Optimal Energy Management Strategies for Hybrid Electric Vehicle. Int. J. Veh. Tech. 2014, 2014. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Li, W.M.; Xu, K.; Zahid, T.M.; Qin, F.Y.; Li, C.M. Energy Management Strategy for a Hybrid Electric Vehicle Based on Deep Reinforcement Learning. Appl. Sci. 2018, 8, 187. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.D.; Peng, J.K.; He, H.W.; Luo, J.Y. Comparative analysis on the rule-based control strategy of two typical hybrid electric vehicle powertrain. Energy Proc. 2016, 104, 384–389. [Google Scholar] [CrossRef]
- Zhao, Y.; Song, H.; Liu, Y.; Yu, Z. Energy Management of Dual Energy Source of Hydrogen Fuel Cell Hybrid Electric Vehicles. SAE Tech. Paper 2020. [Google Scholar] [CrossRef]
- Delprat, S.; Lauber, J.M.; Guerra, T.M.; Rimaux, J. Control of a Parallel Hybrid Powertrain Optimal Control. IEEE Trans. Veh. Technol. 2004, 53, 872–881. [Google Scholar] [CrossRef]
- Lin, C.C.; Peng, H.; Grizzle, J.W.; Kang, J.M. Power Management Strategy for a Parallel Hybrid Electric Truck. IEEE Trans. Contr. Syst. Technol. 2003, 11, 839–849. [Google Scholar] [CrossRef] [Green Version]
- Paganelli, G.; Delprat, S.; Guerra, T.M.; Rimaux, J.; Santin, J.J. Equivalent Consumption Minimization Strategy for Parallel Hybrid Powertrains. In Proceedings of the 55th IEEE Vehicular Technology Conference, Birmingham, AL, USA, 6–9 May 2002; pp. 2076–2081. [Google Scholar] [CrossRef]
- Sciarretta, A.; Back, M.; Guzzella, L. Optimal Control of Parallel Hybrid Electric Vehicles. IEEE Trans. Contr. Syst. Technol. 2004, 12, 352–363. [Google Scholar] [CrossRef]
- Couch, J.; Fiorentini, L.S.; Canova, M. An ECMS-Based Approach for the Energy Management of a Vehicle Electrical System. IFAC Proc. Vol. 2013, 46, 115–120. [Google Scholar] [CrossRef]
- Kang, K.; Sim, K.; Hwang, S.H. Equivalent consumption minimization strategy for parallel plug-in hybrid vehicle. In Proceedings of the KSME Conference, Jeju, Korea, 12–15 July 2017. [Google Scholar]
- Hofman, T.; Purnot, T. A Comparative Study and Analysis of an Optimized Control Strategy for the Toyota Hybrid System. World Electr. Veh. J. 2009, 3, 563–571. [Google Scholar] [CrossRef] [Green Version]
- Hwang, H.Y. Developing Equivalent Consumption Minimization Strategy for Advanced Hybrid System-II Electric Vehicles. Energies 2020, 13, 2033. [Google Scholar] [CrossRef]
- Liu, X.; Qin, D.; Wang, S.Q. Minimum Energy Management Strategy of Equivalent Fuel Consumption of Hybrid Electric Vehicle Based on Improved Global Optimization Equivalent Factor. Energies 2019, 12, 2076. [Google Scholar] [CrossRef] [Green Version]
- Thompson, S.T.; James, B.D.; Huya-Kouadio, J.M.; Houchins, C.; DeSantis, D.A.; Ahluwalia, R.; Wilson, A.R.; Kleen, G.; Papageorgopoulos, D. Direct hydrogen fuel cell electric vehicle cost analysis: System and high-volume manufacturing description, validation, and outlook. J. Power Sources 2018, 399, 304–313. [Google Scholar] [CrossRef]
- Départure, C.M.; Jemeï, S.M.; Boulon, L.; Bouscayrol, A.; Marx, N.G.; Morando, S.M.; Castaings, A. IEEE VTS Motor Vehicles Challenge 2017—Energy Management of a Fuel Cell/Battery Vehicle. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Delarue, P.; Bouscayrol, A.; Semail, E. Generic control method of multileg voltage-source-converters for fast practical implementation. IEEE Trans. Power Electron. 2003, 18, 517–526. [Google Scholar] [CrossRef]
- Liaw, B.Y.; Nagasubramanian, G.; Jungst, R.G.; Doughty, D.H. Modeling of lithium ion cells—A simple equivalent-circuit model approach. Solid State Ion. 2004, 175, 835–839. [Google Scholar] [CrossRef]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. From single cell model to battery pack simulation for Li-ion batteries. J. Power Sources 2009, 186, 500–507. [Google Scholar] [CrossRef]
- Chiang, Y.H.; Sean, W.Y.; Ke, J.C. Online estimation of internal resistance and open-circuit voltage of lithium-ion batteries in electric vehicles. J. Power Sources 2011, 196, 3921–3932. [Google Scholar] [CrossRef]
- Herr, N.; Nicod, J.-M.; Varnier, C.; Jardin, L.; Sorrentino, A.; Gouriveau, R.; Hissel, D.; Péra, M.-C. Decision process to manage useful life of multi-stacks fuel cell systems under service constraint. Renew. Energ 2017, 105, 590–600. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Pei, P.; Song, M. Lifetime prediction and the economic lifetime of Proton Exchange Membrane fuel cells. Appl. Energy 2015, 142, 154–163. [Google Scholar] [CrossRef]
- USDRIVE. Hydrogen Production Tech Team Roadmap. 2017. Available online: https://www.energy.gov/eere/vehicles/downloads/us-drive-hydrogen-production-technical-team-roadmap (accessed on 24 June 2021).
- USDRIVE. Fuel Cell Technical Team Roadmap. 2017. Available online: https://www.energy.gov/eere/vehicles/downloads/us-drive-fuel-cell-technical-team-roadmap (accessed on 24 June 2021).
- Nykvist, B.; Nilsson, M. Rapidly falling cost of battery packs for electric vehicles. Nat. Clim. Chang. 2015, 5, 329–332. [Google Scholar] [CrossRef]













| Symbol | Description | Value |
|---|---|---|
| Inductance of smoothing inductor | 0.25 mH | |
| Resistance of smoothing inductor | 5.5 mΩ | |
| Average efficiency of chopper | 0.95 | |
| - | Power capacity of fuel cell | 16 kW |
| Symbol | Description | Value |
|---|---|---|
| Ohmic internal resistance of battery | 0.028 Ω | |
| Equivalent polarization resistance | 0.1417 Ω | |
| Equivalent polarization capacitance | 3529 F | |
| - | Capacity of battery | 40 Ah |
| Nominal voltage of battery | 80 V | |
| - | Number of cells in series for a module | 6 |
| - | Number of modules in series | 4 |
| Symbol | Description | Value |
|---|---|---|
| Vehicle mass including two passengers | 877.8 kg | |
| Equivalent mass of power train inertia | 17 kg | |
| Rolling resistance coefficient | 0.02 | |
| Gravitational acceleration | 9.81 kg m/s2 | |
| Air density | 1.223 kg/m3 | |
| Aerodynamic drag coefficient | 0.386 | |
| Vehicle frontal area | 1.813 m2 | |
| Radius of the tire | 0.2865 m |
| Item (Unit) | RB | ECMS | D-ECMS |
|---|---|---|---|
| Avg. traction power (kW) | 5.11 | 5.11 | 5.11 |
| H2 consumption (g) | 135.24 | 145.57 | 147.59 |
| Final SOC | 0.5411 | 0.6758 | 0.6851 |
| Additional H2 for recharging battery up to 100% (g) | 113.7 | 79.29 | 76.95 |
| Cost of battery recharging, , ($) | 0.3980 | 0.2775 | 0.2693 |
| Battery degradation () | 2.277 × 10−4 | 0.684 × 10−4 | 0.651 × 10−4 |
| Fuel cell degradation () | 3.217 × 10−4 | 2.749 × 10−4 | 2.744 × 10−4 |
| Driving cost, , ($) | 0.8713 | 0.7870 | 0.7859 |
| Degradation cost, , ($) | 0.3987 | 0.2087 | 0.2063 |
| Global cost, , ($) | 1.2100 | 0.9957 | 0.9922 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, L.; Cho, D.-S.; Ahn, C. Degradation-Conscious Equivalent Consumption Minimization Strategy for a Fuel Cell Hybrid System. Energies 2021, 14, 3810. https://doi.org/10.3390/en14133810
Kwon L, Cho D-S, Ahn C. Degradation-Conscious Equivalent Consumption Minimization Strategy for a Fuel Cell Hybrid System. Energies. 2021; 14(13):3810. https://doi.org/10.3390/en14133810
Chicago/Turabian StyleKwon, Laeun, Dae-Seung Cho, and Changsun Ahn. 2021. "Degradation-Conscious Equivalent Consumption Minimization Strategy for a Fuel Cell Hybrid System" Energies 14, no. 13: 3810. https://doi.org/10.3390/en14133810
APA StyleKwon, L., Cho, D.-S., & Ahn, C. (2021). Degradation-Conscious Equivalent Consumption Minimization Strategy for a Fuel Cell Hybrid System. Energies, 14(13), 3810. https://doi.org/10.3390/en14133810